改进粒子群优化BP神经网络的目标威胁估计

引用本文

黄璇, 郭立红, 李姜, 于洋. 改进粒子群优化BP神经网络的目标威胁估计. 吉林大学学报(工学版), 2017, 47(3): 996-1002
HUANG Xuan, GUO Li-hong, LI Jiang, YU Yang. Target threat assessment based on BP neural network optimized by modified particle swarm optimization. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 996-1002 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703042
Permissions

改进粒子群优化BP神经网络的目标威胁估计

黄璇^1,², 郭立红¹, 李姜², 于洋²

1.中国科学院长春光学精密机械与物理研究所,长春 130033

2.中国科学院大学,北京 100039

郭立红(1964-),女,研究员,博士.研究方向:光电对抗装备总体设计.E-mail:guolh@ciomp.ac.cn

作者简介:黄璇(1988-),男,博士研究生.研究方向:多源引导信息融合.E-mail:huangxuan@ceprei.biz

基金项目:国家自然科学基金项目(61205143)

摘要

为了提高目标威胁估计精度,提出一种运用改进粒子群算法优化BP神经网络的方法。为了避免陷入局部极值,将变异过程引入粒子群算法中,并对相关参数进行优化,形成改进粒子群算法,对BP神经网络的初始权值和阈值进行优化。利用样本数量不同的训练集对网络进行训练,并用60组测试集数据对网络进行验证。实验结果表明,改进粒子群优化BP神经网络目标威胁估计算法具有更高的预测精度,在训练样本数量较小时能够获得较好的预测能力,可以有效地完成目标威胁估计。

关键词: 信息处理技术; 威胁估计; 粒子群优化算法; BP神经网络; 参数优化

中图分类号:TP391.9 文献标志码:A 文章编号:1671-5497(2017)03-0996-07

Target threat assessment based on BP neural network optimized by modified particle swarm optimization

HUANG Xuan^1,², GUO Li-hong¹, LI Jiang², YU Yang²

1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

2.University of Chinese Academy of Sciences, Beijing 100039,China

Abstract

An algorithm for target threat assessment based on Back Propagation (BP) neural network optimized by Modified Particle Swarm Optimization (MPSO) is proposed to improve the prediction accuracy of target threat. In this MPSO algorithm, mutation operator and optimization for several parameters are introduced in PSO to avoid the particle plunging into the local optimization. The MPSO algorithm is employed to optimize the initial weights and thresholds of the BP neural network. Then the BP neural network optimized by MPSO is trained by training sets of different sample sizes. 60 sets of target threat data are adopted to test the performance of MPSO-BP in target threat prediction. Experimental results show that the prediction accuracy of target threat assessment algorithm based on MPSO-BP is higher than that based on some traditional algorithms, which proves the efficiency of the proposed algorithm in solving target threat assessment problem in spite of the small sample size of training set.

Key words: information processing technology; threat assessment; particle swarm optimization(PSO) algorithm; BP neural network; parameter optimization

Show Figures

0 引言

对敌方目标进行威胁估计, 主要是对其杀伤能力和威胁程度进行估计。威胁估计在信息融合模型中处于第3级, 对于估计作战事件出现的严重程度有重要作用, 为决策和指挥提供支持。目前常用的目标威胁估计方法包括Bayes推理^[1]、直觉模糊集^[2]、层次分析法^[3]、Vague集^[4]、支持向量机等^{[5, 6]}。

近年来, 智能技术, 特别是神经网络技术在控制^{[7, 8]}、图像处理^[9]等领域得到了广泛应用。文献[10]成功地将BP(Back propagation)神经网络应用于目标威胁估计之中。但是, 神经网络容易陷入局部极值, 特别是对于处理小样本、高维度问题, 其收敛速度会变慢, 网络性能也会变差。此外, 一旦初始权值和阈值选取不恰当, 将使其难以收敛, 无法获得较好的预测效果。

粒子群优化(Particle swarm optimization, PSO)算法是一种较新的群智能优化算法, 可以对各种连续和离散问题的参数进行寻优操作, 具有精度高、收敛快的特点, 在目标跟踪^[11]、参数辨识^[12]、信号处理^[13]等领域有较好的应用。然而PSO算法也具有容易陷入局部最优解的缺点, 导致经过寻优获得的参数在处理BP网络小样本训练问题时可能还不如未经优化的网络。

为解决PSO算法容易陷入局部极值的问题, 本文对PSO算法的相关参数进行改进, 并引入变异运算, 形成改进的粒子群优化(Modified particle swarm optimization, MPSO)算法, 以此建立改进粒子群优化BP神经网络(BP neural network optimized by modified PSO, MPSO-BP)算法。运用个体粒子代表网络的权值和阈值, 以网络的预测误差作为个体粒子的适应度, 通过MPSO算法对粒子进行寻优, 得到最优解, 并以此来构造BP神经网络。最后, 采集样本数量不同的目标威胁估计训练集对MPSO-BP进行训练, 运用测试集数据验证网络的预测性能, 并与BP、PSO-BP算法的性能进行比较。

1 粒子群优化算法

1.1 基本粒子群优化算法

PSO算法^[14]是一种经典的群智能算法, 由以下4部分构成:①初始化; ②适应度计算; ③极值更新; ④位置和速度更新。

假设在S维空间中, 种群X=(X₁, X₂, …, X_n)中的每一项代表一个粒子。各项有其相应的位置, 即优化问题的一个可能的解, 用S维向量X_i= $\begin{matrix} {(x_{i 1}, x_{i 2}, \dots, x_{iS})}^{T} \end{matrix}$ (i=1, 2, …, n)来表示, 其速度V_i= $\begin{matrix} {(v_{i 1}, v_{i 2}, \dots, v_{iS})}^{T} \end{matrix}$ 。根据目标函数可以计算其适应度。迭代时有两个主要的依据, 一个是个体极值P_i= $\begin{matrix} {(P_{i 1}, P_{i 2}, \dots, P_{iS})}^{T} \end{matrix}$ , 表示某一个体在迭代历史中的得到其最优适应度时所在的位置; 另一个是全局极值P_g= $\begin{matrix} {(P_{g 1}, P_{g 2}, \dots, P_{gS})}^{T} \end{matrix}$ , 表示全体在迭代历史中得到最优适应度时所在的位置。迭代时粒子的速度和位置可以根据P_i和P_g按照式(1)(2)进行更新:

$v_{ij}^{k + 1} = ω v_{ij}^{k} + c_{1} r_{1} (P_{ij}^{k} - x_{ij}^{k}) + c_{2} r_{2} (P_{gj}^{k} - x_{ij}^{k})$ （1）

$\begin{matrix} x_{ij}^{k + 1} = x_{ij}^{k} + v_{ij}^{k + 1} \end{matrix}$ （2）

式中:k代表当前处于第k次迭代; ω 为惯性权重; j=1, 2, …, S; c₁和c₂分别为局部加速因子和全局加速因子; r₁和r₂为[0, 1]间随机数; ω $\begin{matrix} v_{ij}^{k} \end{matrix}$ 为粒子的惯性行为; c₁r₁( $\begin{matrix} P_{ij}^{k} \end{matrix}$ - $\begin{matrix} x_{ij}^{k} \end{matrix}$ )为粒子对自身实力进行认知的行为; c₂r₂( $\begin{matrix} P_{gj}^{k} \end{matrix}$ - $\begin{matrix} x_{ij}^{k} \end{matrix}$ )为粒子对周围环境进行认知的行为。

粒子根据自身和全局的经验向最优位置搜索移动。迭代时需保证x∈ $\begin{matrix} [x_{\min}, x_{\max}] \end{matrix}$ , v∈ $\begin{matrix} [v_{\min}, v_{\max}] \end{matrix}$ 。

基本PSO算法使用简单、寻优速度较快, 但同时也存在如下问题:

(1)局部极值问题:算法迭代时, 所有粒子都向当前最优解移动, 种群搜索空间不断缩小, 形成粒子种群快速趋同效应^[15], 但是此时的最优位置可能只是某一局部搜索空间里的最优位置, 搜索陷入局部极值之中, 导致早熟收敛, 失去粒子之间所需要保持的多样性。

(2)收敛精度问题:粒子在搜索移动时, 受惯性行为ω $\begin{matrix} v_{ij}^{k} \end{matrix}$ 的影响, 当惯性因子较大时, 粒子的收敛速度会很快, 但当粒子靠近最优解时又会受到高惯性权重的影响而不能精细地搜索, 使得收敛精度不高。

基本PSO算法的这些问题会导致当训练样本数较低时, 对网络进行优化后的预测误差甚至会大于未经过优化的。因此, 为了提高预测精度, 使其能在小样本训练中发挥作用, 需对PSO算法进行改善。

1.2 改进粒子群优化算法

局部极值的产生, 是基本PSO算法在迭代更新时由于粒子对自身和全局环境认知的分配不均而引起的。因此需要在迭代过程中, 对粒子的自身历史能力认知和全局环境认知进行动态分配。基于此, 对基本PSO算法进行如下改进:

(1)对参数的改进

惯性权重ω 用于保持运动的惯性, 调节所搜索区域的大小, 而因子c₁和c₂则代表了将其推向P_i和P_g的权重。在迭代初期, 粒子应在一个较大的范围内去搜索最优解, 并且粒子移动应以自身认知为主, 保持粒子的多样性, 故此时ω 和c₁应较大而c₂较小; 而在迭代后期, 粒子应更多地受控于此时的全局最优解, 并在其附近进行精细的局部搜索, 故此时ω 和c₁应较小而c₂较大。基于此, 本文在每次迭代时对3个参数进行如下操作:

$\begin{matrix} \{\begin{matrix} ω^{k} = [(ω_{0} - ω_{1}) \cos (πk / K) + (ω_{0} + ω_{1})] / 2 \\ c_{1}^{k} = c_{10} - (c_{10} - c_{11}) (1 - k / K) \\ c_{2}^{k} = c_{20} + (c_{21} - c_{20}) (1 - k / K) \end{matrix} \end{matrix}$ （3）

式中:ω ₀、ω ₁分别为ω 的起始取值和最终取值; c₁₀、c₁₁分别为c₁的起始取值和最终取值; c₂₀、c₂₁分别为c₂的起始取值和最终取值; k、K分别为迭代次数的当前取值和最大取值。

c₁随着迭代次数线性递减, c₂则线性递增, 并且初始的c₁₀应大于c₂₀, 终止时的c₁₁小于c₂₁, 即迭代初期侧重于自身认知, 末期侧重于全局认知, 从而保证粒子对自身认知能力和全局认知能力的动态分配。ω 按照余弦函数递减, 既保证了迭代开始阶段能快速搜寻最优解且持续较长时间, 不至于过早地陷入局部搜索, 又能在迭代后期以一个较为平缓的速度变化率去进行精细搜索。

(2)引入变异操作

为进一步扩大搜索空间, 减小出现局部极值的可能, 每次更新之后, 对粒子按照一定的概率p重新初始化, 即:

$\begin{matrix} x_{ij} = \{\begin{matrix} x_{ij} + (x_{ij} - x_{\min}) (1 - k / K) a, a > 0.5 \\ x_{ij} - (x_{ij} - x_{\max}) (1 - k / K) a, a \leq 0.5 \end{matrix} \end{matrix}$ （4）

式中:a为[0, 1]内的一个随机数, 决定粒子朝向最大或最小的方向变异。

变异概率p由式(5)确定:

$\begin{matrix} p^{k} = [(p_{1} + p_{0}) - (p_{1} - p_{0}) \cos (πk / K)] / 2 \end{matrix}$ （5）

式中:p₀、p₁分别为p的起始取值和最终取值, 令p₀< p₁, 使得p的取值按余弦函数递增。

由于迭代初期的搜索空间较大, 因而变异概率可以较小, 粒子在前述3个参数确定的范围内搜索和移动即可; 而迭代后期由于粒子向最优解移动, 搜索空间范围已经较小, 此时加大变异概率可以进一步防止陷入局部极值。

2 基于MPSO-BP的目标威胁估计

作为一种高级信息融合过程, 威胁估计是在综合考虑敌方破坏力、运动能力、机动能力等因素的基础上, 对敌方的战术含义和威胁程度或严重性进行估计。按照属性特征划分, 威胁估计因素包括目标速度、航向角等定量因素和目标类型、干扰能力等定性因素。本文选取目标速度(V)、目标航向角(θ )、目标高度(H)、目标距离(R)、目标类型、目标干扰能力6个典型指标, 构建如图1所示的MPSO-BP算法。

	Figure Option View Download New Window
	图1 MPSO-BP算法流程图Fig.1 Flowchart of MPSO-BP algorithm

该算法可以分为两部分, 一是图中左侧的MPSO优化部分; 二是图中右侧的网络训练部分。运用左侧MPSO的粒子代表右侧所确定网络的权值和阈值, 以右侧网络所求得的预测误差作为此粒子的适应度, 以适应度值为基础按照MPSO方法对粒子进行寻优, 通过迭代更新找到最优的个体粒子, 以此作为网络的初始权值和阈值。

(1)初始化

包括网络结构的确定、种群的编码以及各个参数的选取。其中, 采用三层网络结构, 每个个体需包含全部的权值和阈值, 即输出层(Output layer)与隐层(Hidden layer)、隐层与输入层(Input layer)的连接权值以及输出层和隐层的阈值。因此, 粒子的维度S应为:

$\begin{matrix} S = S_{in} S_{h} + S_{h} S_{out} + S_{h} + S_{out} (6) \end{matrix}$

式中:S_in、S_h、S_out分别为输入层、隐层和输出层的结点数。

对于目标威胁估计问题, 6个典型指标对应6个输入层, 网络输出为威胁估计值, 因此输出层结点数为1, 隐层有11个结点。维度S=89, 包含77个权值和12个阈值。

(2)适应度函数选取

将误差作为MPSO的适应度, 即:

$\begin{matrix} F_{i} = \overset{M}{\sum_{j = 1}} ({\hat{y}}_{ij} - {\bar{y}}_{ij})^{2} \end{matrix}$ （7）

式中: $\begin{matrix} {\hat{y}}_{ij} \end{matrix}$ 、 $\begin{matrix} {\bar{y}}_{ij} \end{matrix}$ 分别为训练的实际输出值和期望输出值; M为网络Output layer的结点数, 在目标威胁估计问题中, 有M=1。

(3)迭代更新

在MPSO优化阶段, 利用式(7)计算每个粒子的F_i, 以此确定每次的P_i和P_g; 利用式(1)(2)对位置x_i和速度v_i进行更新, 每次更新时, 利用式(3)确定各个参数的取值; 在每次更新后, 按照式(5)确定的概率重新对x_i初始化(见式(4))。

更新后, 重新计算适应度F_i, 并根据F_i更新P_i和P_g的取值。重复迭代操作, 直至满足k=K, 从而获得最优解。

3 MPSO-BP算法验证

3.1 仿真参数设置

运用Matlab R2009a, 编程实现MPSO-BP目标威胁估计算法。从目标威胁数据库中按均匀分布随机抽取300组原始数据作为训练集, 按照目标类型分类, 大型目标、小型目标、直升机各100组数据。再用同样的分类方式抽取60组数据组成测试集。部分的原始数据如表1所示。原始数据需在归一化后再注入到MPSO-BP算法中。

对于MPSO部分, 设置种群规模n=30; 最大迭代次数K=300; 粒子位置区间为[-5, 5], 粒子速度取值区间为[-1, 1]; 其他变化的参数为:c₁₀=2.5、c₁₁=1.25、c₂₀=0.5、c₂₁=2.5、P₀=0.05、P₁=0.35、ω ₀=1以及ω ₁=0.1。网络部分, 设置学习率为0.1, 训练目标为1.0× 10^-5。

表1 部分原始数据 Table 1 Part of original data

为了验证MPSO-BP目标威胁估计算法的有效性, 本文采用BP网络和PSO-BP网络解决目标威胁估计问题。对于前者, 其参数设置与本文方法的BP部分相同; 对于后者, 则不引入变异过程且设置c₁=1.4、c₂=1.6、ω =1, 其余部分与本文方法相同。

3.2 仿真结果

采用经过全部训练集数据训练后的3种方法对全部威胁估计测试数据进行预测。获得各方法的预测结果及误差如图2所示。

	Figure Option View Download New Window
	图2 训练集样本为300时的预测结果及误差Fig.2 Predictive results and errors with 300 training samples

从图2中可以看出, 3种算法都可以较好地对60组测试集数据完成目标威胁估计, 绝对误差均不大于0.012, 大都在0.01以内。在其中的41个样本点处(约占总样本量的2/3), MPSO-BP网络的预测误差要小于另外两种算法, MPSO-BP的绝对误差平均值也是三者中最小的。

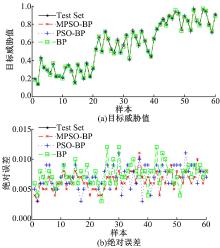
从300组训练集数据中按照目标类别1∶ 1∶ 1的比例随机抽取150组, 同样再对3种网络进行训练, 采用训练好的3种网络对同样的测试集进行目标威胁估计, 预测结果及误差如图3所示。

	Figure Option View Download New Window
	图3 训练集样本为150时的预测结果及误差Fig.3 Predictive results and errors with 150 training samples

从图3可以看出, 当训练样本数量减少为150时, 3种算法的预测误差均有所增加, PSO-BP和BP网络的平均误差增加约40%。而本文网络的预测误差基本都小于0.01, 展现出较好的预测能力。

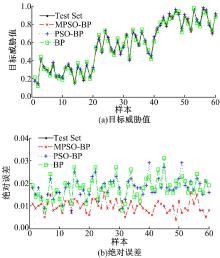
从300组训练集数据中按照目标类别1∶ 1∶ 1的比例随机抽取75组, 同样对3种网络进行训练, 并对同样的测试集进行目标威胁估计, 结果及误差如图4所示。

	Figure Option View Download New Window
	图4 训练集样本为75时的预测结果及误差Fig.4 Predictive results and errors with 75 training samples

从图4可以看出, 当训练样本数量减少为最初的1/4时, PSO-BP和BP网络的误差急剧增加, 后者的最大误差达到了0.031, 而前者的平均误差甚至要大于后者, 没有展现出算法应有的优化效果。而本文方法的预测误差集中在0.01附近, 并且平均值小于0.01, 展现出较好的预测能力。

表2给出了在经过不同样本数量的训练集数据训练后, MPSO-BP网络、PSO-BP网络和BP网络对于60组目标威胁估计测试集数据的绝对预测误差的平均值。

从图2~图4和表2误差的变化可以看出, 当所采用的训练集中样本数量较大时, 3种网络的精度相当, 都能较好地解决目标威胁估计问题, MPSO-BP的预测误差略小于另外两种网络。而当所采用的训练集中样本数量较小时, PSO-BP方法容易产生局部极值, 其预测误差反而大于未经优化的原始网络。而对于MPSO-BP算法, 由于加入了变异过程, 可以有效地避免粒子种群快速趋同效应, 其预测结果最接近真实值, 预测误差为三者中最小, MPSO-BP算法通过较小的训练代价即可获得较高的预测精度。

表2 三种网络在不同样本数下的绝对误差平均值 Table 2 Average of absolute predictive error of three networks with different quantities of training set

4 结束语

根据目标威胁估计的特点, 综合考虑各种影响因素, 提出了基于MPSO-BP的目标威胁估计方法。选取6个典型指标, 在训练集样本数量不同的情况下分别对BP网络、PSO-BP网络和MPSO-BP网络进行仿真实验比较。结果表明:在训练集较少的情况下, 本文方法能够克服快速趋同效应的影响, 降低陷入局部极值的可能, 其预测误差小于另外两种网络。因此, 基于改进粒子群算法优化的BP神经网络具有良好的预测能力, 可以有效地完成对作战目标威胁的估计。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王小龙, 宋裕农, 丁文强. 基于分层贝叶斯网络的反潜编队对潜威胁估计[J]. 火力与指挥控制, 2014, 39(4): 82-85. Wang Xiao-long, Song Yu-nong, Ding Wen-qiang. Method for evaluate threat of anti-submarine war fleet to submarine based on hierarchical bayesian network[J]. Fire Control and Command Control, 2014, 39(4): 82-85. [本文引用:1]
[2]	王毅, 刘三阳, 张文, 等. 属性权重不确定的直觉模糊多属性决策的威胁评估方法[J]. 电子学报, 2014, 42(12): 2509-2514. Wang Yi, Liu San-yang, Zhang Wen, et al. Threat assessment method with uncertain attribute weight based on intuitionistic fuzzy multi-attribute decision[J]. Acta Electronica Sinica, 2014, 42(12): 2509-2514. [本文引用:1]
[3]	谷向东, 童中翔, 柴世杰, 等. 基于IAHP和离差最大化TOPSIS法目标威胁评估[J]. 空军工程大学学报: 自然科学版, 2011, 12(2): 27-31. Gu Xiang-dong, Tong Zhong-xiang, Chai Shi-jie, et al. Target threat assessment based on TOPSIS combined by IAHP and the maximal deviation[J]. Journal of Air Force Engineering University(Natural Science Edition), 2011, 12(2): 27-31. [本文引用:1]
[4]	耿涛, 卢广山, 张安. 基于Vague集的空中目标威胁评估群决策方法[J]. 系统工程与电子技术, 2011, 33(12): 2686-2690. Geng Tao, Lu Guang-shan, Zhang An. Group decision-making method for air target threat assessment based on Vague sets[J]. Systems Engineering and Electronics, 2011, 33(12): 2686-2690. [本文引用:1]
[5]	黄璇, 郭立红, 李姜, 等. 磷虾群算法优化支持向量机的威胁估计[J]. 光学精密工程, 2016, 24(6): 1448-1455. Huang Xuan, Guo Li-hong, Li Jiang, et al. Three assessment of support vector machine optimized by Krill Herd algorithm[J]. Optics and Precision Engineering, 2016, 24(6): 1448-1455. [本文引用:1]
[6]	李姜, 郭立红. 基于改进支持向量机的目标威胁估计[J]. 光学精密工程, 2014, 22(5): 1354-1362. Li Jiang, Guo Li-hong. Target threat assessment using improved SVM[J]. Optics and Precision Engineering, 22(5): 1354-1362. [本文引用:1]
[7]	程帅, 孙俊喜, 曹永刚, 等. 增量深度学习目标跟踪[J]. 光学精密工程, 2015, 23(4): 1161-1170. Cheng Shuai, Sun Jun-xi, Cao Yong-gang, et al. Target tracking based on incremental deep learning[J]. Optics and Precision Engineering, 2015, 23(4): 1161-1170. [本文引用:1]
[8]	赵博, 李成浩, 李元春. 基于故障在线估计的可重构机械臂分散容错控制[J]. 吉林大学学报: 工学版, 2014, 44(6): 1729-1735. Zhao Bo, Li Cheng-hao, Li Yuan-chun, et al. Online fault estimation based on decentralized fault tolerant control for reconfigurable manipulators[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1729-1735. [本文引用:1]
[9]	杨娜, 陈后金, 李艳凤, 等. 基于改进的脉冲耦合神经网络模型的图像分割[J]. 吉林大学学报: 工学版, 2013, 43(3): 758-763. Yang Na, Chen Hou-jin, Li Yan-feng, et al. Algorithm of image segmentation based on the improved pulse coupled neural network model[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 758-763. [本文引用:1]
[10]	罗艳春, 郭立红, 姜晓莲, 等. 基于模糊神经网络的空中目标威胁估计[J]. 微计算机信息, 2007, 23(34): 268-270. Luo Yan-chun, Guo Li-hong, Jiang Xiao-lian, et al. Threat assessment for aerial target based on fuzzy neural network[J]. Microcomputer Information, 2007, 23(34): 268-270. [本文引用:1]
[11]	李东年, 周以齐. 采用改进粒子群优化粒子滤波的三维人手跟踪[J]. 光学精密工程, 2014, 22(10): 2870-2878. Li Dong-nian, Zhou Yi-qi. Three dimensional hand tracking by improved particle swarm optimized particle filter[J]. Optics and Precision Engineering, 2014, 22(10): 2870-2878. [本文引用:1]
[12]	刘青, 李阳. 基于多尺度径向基函数的时变系统辨识[J]. 北京航空航天大学学报, 2015, 41(9): 1722-1728. Liu Qing, Li Yang. Identification of time-varying systems using multi-scale radial basis function[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(9): 1722-1728. [本文引用:1]
[13]	Ko C N, Chang Y P, Wu C J, et al. A PSO method with nonlinear time-varying evolution for optimal design of harmonic filter[J]. IEEE Transactions on Power Systems, 2009, 23(1): 437-444. [本文引用:1]
[14]	Kennedy J, Eberhart R C. Particle swarm optimization[C]//Proceeding of the IEEE International Conference on Neural Networks, Perth, Australia, 1995: 1942-1948. [本文引用:1]
[15]	Ling S H, Iu H, Leung F H, et al. Improved hybrid particle swarm optimized wavelet neural network for modeling the development of fluid dispensing for electronic packaging[J]. IEEE Transactions on Industrial Electronics, 2008, 55(9): 3447-3460. [本文引用:1]

2014

0.0

. 2014, 39(4):82-85 DOI:doi:10.3969/j.issn.1002-0640.2014.04.020

Method for evaluate threat of anti-submarine war fleet to submarine based on hierarchical bayesian network

基于分层贝叶斯网络的反潜编队对潜威胁估计

Wang Xiao-long , Song Yu-nong , Ding Wen-qiang.

王小龙, 宋裕农, 丁文强

应用贝叶斯网络模型进行威胁估计是当前研究的热点和难点。提出了应用分层贝叶斯网络模型构建威胁估计网络，用于估计反潜编队对潜威胁等级。首先，对分层贝叶斯网络模型进行了简要的阐述，并对利用该模型进行威胁估计的可行性进行了分析。其次，分析了反潜编队对潜威胁产生的原因和机理，在此基础上，构建了威胁估计网络。最后，通过算例仿真验证了威胁估计网络的有效性。

... 目前常用的目标威胁估计方法包括Bayes推理^[1]、直觉模糊集^[2]、层次分析法^[3]、Vague集^[4]、支持向量机等^[5,6] ...

2014

0.0

. 2014, 42(12):2509-2514 DOI:doi:10.3969/j.issn.0372-2112.2014.12.025

Threat assessment method with uncertain attribute weight based on intuitionistic fuzzy multi-attribute decision

属性权重不确定的直觉模糊多属性决策的威胁评估方法

Wang Yi , Liu San-yang , Zhang Wen

王毅, 刘三阳, 张文

Under the framework of IFS(Intuitionistic Fuzzy Sets),aiming at the situation that targets' attributes are interval value,the weights are totally unknown,and decision-makers have preference information,a threat assessment method with uncertain attribute weight based on intuitionistic fuzzy multi-attribute decision is proposed.Firstly,based on the above-mentioned problem,intuitionistic fuzzy interval judgment matrix is set up,and a standard interval value index processing method is put forward;secondly,by analyzing the target attribute,attribute weight,and decision-makers' authority degree in project,the preference project model in group decision making is finally constructed;thirdly,according to the attribute's variety character in interval value,the definition of intuitionistic fuzzy interval value's similarity and ideal resolve is given,and the optimization attribute weight restriction model is built up;lastly,some typical threat assessment examples are cited to verify that the method can reflect the influence of both subjective and objective information,which can avoid the deviation caused by sensor invalidation,outside environment's effect,or decision-makers' subjective experience.Finally,the superiority of the method is proved by the threat assessment of some typical targets.

在直觉模糊集的框架下,重点研究了目标属性值为区间数且权重完全未知,决策者对方案具有偏好信息的问题,提出一种属性权重不确定的直觉模糊多属性决策的威胁评估方法.首先,针对上述问题,建立了直觉模糊区间判断矩阵,给出了目标属性为区间数的指标值规范化处理方法;其次,分析了决策者对方案中所涉及的目标属性、属性权重及决策者权威度,建立了群决策的方案偏好模型;再次,针对目标属性值在某一区间内变化的特点,给出了直觉模糊区间值的接近度与理想解的定义,建立了最优属性权重约束优化模型;最后,以典型的威胁评估实例验证了该方法可同时反映主观和客观信息对目标威胁评估的影响,可有效避免因部分传感器失效或受外界环境因素影响以及决策者主观经验所带来的偏差,实际目标威胁评估结果验证了该方法的优越性.

... 目前常用的目标威胁估计方法包括Bayes推理^[1]、直觉模糊集^[2]、层次分析法^[3]、Vague集^[4]、支持向量机等^[5,6] ...

2011

0.0

. 2011, 12(2):27-31 DOI:doi:10.3969/j.issn.1009-3516.2011.02.006

Target threat assessment based on TOPSIS combined by IAHP and the maximal deviation

基于IAHP和离差最大化TOPSIS法目标威胁评估

Gu Xiang-dong , Tong Zhong-xiang , Chai Shi-jie

谷向东, 童中翔, 柴世杰

针对空战目标威胁评估问题,综合考虑了主观和客观因素,将运用区间层次分析法(Interval-based AHP,IAHP)求解出的威胁评估指标主观权重与运用离差最大化法求解出的威胁评估指标客观权重相融合得到组合权重.建立了改进的TOPSIS法评估空战目标威胁的数学模型,首先构造加权规范化决策矩阵,其次确定区间型正理想解和负理想解,然后计算每个目标分别到正理想解和负理想解的距离,最后计算每个目标对理想解的贴近度.给出评估实例,在3种不同权重影响因子组合的情况下,最终求解得到相同的目标威胁评估排序,评估结果表明:该方法合理有效,并针对原方法有了较大改进.

... 目前常用的目标威胁估计方法包括Bayes推理^[1]、直觉模糊集^[2]、层次分析法^[3]、Vague集^[4]、支持向量机等^[5,6] ...

2011

0.0

. 2011, 33(12):2686-2690 DOI:doi:10.3969/j.issn.1001-506X.2011.12.21

Group decision-making method for air target threat assessment based on Vague sets

基于Vague集的空中目标威胁评估群决策方法

Geng Tao , Lu Guang-shan , Zhang An.

耿涛, 卢广山, 张安

Subjective threat evaluation is necessary for air target threat assessment. A group decision-making method based on Vague sets is used to accomplish this evaluation. Vague values are used to express the decision-maker’s uncertainty subjective preference in the air target threat assessment, and a Vague entropy induced ordered weighted averaging (VE-IOWA) operator is proposed to synthesize these Vague values, which can eliminate the harmful uncertainty man-made accidents in the process. Then a decision method based on the distance of Vague values and the optimal and inferior point method is put forward to sort the target threats. Examples confirm the method is feasible and more effective than the fuzzy comprehensive evaluation method.

主观威胁评估方法是空中目标威胁评估的必要手段。将基于Vague集的群决策方法用于空中目标的主观威胁评估，用Vague数表示决策者对目标威胁度的主观评价值，提出一种Vague熵诱导的有序加权平均算子，用于集结各个Vague评价值，可以消除集结过程中人为误差带来的不良影响。为了直观评估各目标威胁程度大小，还提出一种基于Vague数距离和优劣点法的决策方法，来对目标威胁度进行比较和排序。算例证明该方法在空中目标威胁评估中是可行的，而且比常用的模糊综合评估方法更加有效。

... 目前常用的目标威胁估计方法包括Bayes推理^[1]、直觉模糊集^[2]、层次分析法^[3]、Vague集^[4]、支持向量机等^[5,6] ...

2016

0.0

. 2016, 24(6):1448-1455

Three assessment of support vector machine optimized by Krill Herd algorithm

磷虾群算法优化支持向量机的威胁估计

Huang Xuan , Guo Li-hong , Li Jiang

黄璇, 郭立红, 李姜

To put forward the method of threat assessment of support vector machine optimized by Krill Herd algorithm based on the traditional support vector machine optimization method, so as to improve the forecast precision of target threat assessment. The thesis introduces the principles of Krill Herd algorithm and support vector machine and optimize the penalty parameter and kernel function parameter in the support vector machine with Krill Herd algorithm to find the optimal penalty parameter and kernel function parameter; establishes the model of target threat assessment of the support vector machine optimized by Krill Herd algorithm and achieves the target threat assessment algorithm based on this model. Collect 90 sets of original data to form the training set and 30 sets of data to form the test set to carry out simulation experiment on the target threat assessment algorithm. The experimental result shows that the forecast error of the support vector machine optimized by Krill Herd algorithm is 0.002 91 which is less than that of the support vector machine optimized by particle swarm algorithm or firefly algorithm. It can conclusion that the target threat assessment method of the support vector machine optimized by Krill Herd algorithm can effectively complete the target threat assessment.

... 目前常用的目标威胁估计方法包括Bayes推理^[1]、直觉模糊集^[2]、层次分析法^[3]、Vague集^[4]、支持向量机等^[5,6] ...

2014

0.0

. 2014, 22(5):1354-1362 DOI:doi:10.3788/OPE.20142205.1354

基于改进支持向量机的目标威胁估计

Li Jiang , Guo Li-hong.

李姜, 郭立红

摘　要：针对信息融合中目标威胁估计的特点,分析了传统目标威胁估计方法和支持向量机（SVM）的不足。采用粒子群算法（PSO）对SVM中惩罚参数c和核函数g进行优化,建立了改进的SVM（PSO_SVM）目标威胁估计模型及算法。介绍了粒子群算法和支持向量机的原理,建立了一种新的PSO_SVM目标威胁估计模型；基于该模型,实现了PSO_SVM目标威胁估计算法。为适应该算法,对数据进行了预处理,包括数据量化和归一化。交叉验证寻找最佳参数时,采用PSO算法进行优化。采集75组原始数据用于仿真实验,其中60组作为训练集,15组作为测试集。仿真实验表明,该算法预测误差为0,达到了预期目标。实验结果真实、准确地反映了实际情况,证明了该方法的有效性。

... 目前常用的目标威胁估计方法包括Bayes推理^[1]、直觉模糊集^[2]、层次分析法^[3]、Vague集^[4]、支持向量机等^[5,6] ...

2015

0.0

. 2015, 23(4):1161-1170

Target tracking based on incremental deep learning

增量深度学习目标跟踪

Cheng Shuai , Sun Jun-xi , Cao Yong-gang

程帅, 孙俊喜, 曹永刚

... 近年来,智能技术,特别是神经网络技术在控制^[7,8]、图像处理^[9]等领域得到了广泛应用 ...

2014

0.0

. 2014, 44(6):1729-1735 DOI:doi:10.13229/j.cnki.jdxbgxb201406030

Online fault estimation based on decentralized fault tolerant control for reconfigurable manipulators

基于故障在线估计的可重构机械臂分散容错控制

Zhao Bo , Li Cheng-hao , Li Yuan-chun

赵博, 李成浩, 李元春

摘　要：为了降低可重构机械臂模块关节执行器和传感器故障对其控制性能的影响,提出了一种基于故障在线估计的分散容错控制方法。基于可重构机械臂的模块化属性和Lyapunov稳定性理论,设计了分散自适应滑模观测器以实现执行器和传感器故障的在线自适应估计。同时采用神经网络对子系统非线性项进行逼近和补偿,并结合非奇异快速Terminal滑模思想实现了分散容错控制。最后,采用两种不同构形的三自由度可重构机械臂进行了仿真试验,结果表明,所设计的容错控制方法是有效的。

... 近年来,智能技术,特别是神经网络技术在控制^[7,8]、图像处理^[9]等领域得到了广泛应用 ...

2013

0.0

. 2013, 43(3):758-763 DOI:doi:10.7964/jdxbgxb201303033

Algorithm of image segmentation based on the improved pulse coupled neural network model

基于改进的脉冲耦合神经网络模型的图像分割

Yang Na , Chen Hou-jin , Li Yan-feng

杨娜, 陈后金, 李艳凤

摘　要：提出了一种改进的脉冲耦合神经网络（Receptive field-pulse coupled neural net-works,RF-PCNN）模型。通过感受野模型对连接矩阵的优化,使脉冲耦合神经网络（Pulsecoupled neural networks,PCNN）模型具有了方向性和尺度性,能够更好地模拟视觉细胞图像分割的功能。试验结果表明：RF-PCNN模型对自然环境中车辆图像分割的有效性,分割结果具有较高的边界检出率,较好地解决了图像分割中车牌区域存在的欠分割和过分割问题。

... 近年来,智能技术,特别是神经网络技术在控制^[7,8]、图像处理^[9]等领域得到了广泛应用 ...

2007

0.0

. 2007, 23(34):268-270

Threat assessment for aerial target based on fuzzy neural network

基于模糊神经网络的空中目标威胁估计

Luo Yan-chun , Guo Li-hong , Jiang Xiao-lian

罗艳春, 郭立红, 姜晓莲

2014

0.0

. 2014, 22(10):2870-2878 DOI:doi:10.3788/OPE.20142210.2870

Three dimensional hand tracking by improved particle swarm optimized particle filter

采用改进粒子群优化粒子滤波的三维人手跟踪

Li Dong-nian , Zhou Yi-qi.

李东年, 周以齐

针对高维人手状态空间中的采样稀疏问题,提出了一种基于改进粒子群优化粒子滤波的关节人手跟踪方法,用于从Kinect获取的深度图像序列中恢复三维人手运动.首先,利用简单几何基元建立三维人手模型,并为其添加自由度节点,用于在跟踪过程中生成可与观测特征进行比较的人手姿势假设.然后,在粒子滤波框架下,使用深度图像作为观测输入,融合深度特征与区域特征建立了系统观测模型.最后,将粒子群优化粒子滤波应用于关节人手运动跟踪.为避免在高维空间中的早熟收敛问题,利用模拟退火思想和局部随机化方法对算法进行改进, 增强了算法的全局搜索能力.通过合成序列和真实序列上的跟踪实验对该方法进行了评价,结果表明该方法的关节角度跟踪误差均值约为2.3°,标准差约为 1.7°,优于标准粒子滤波和标准粒子群优化跟踪方法,可以准确、鲁棒地从深度图像跟踪三维人手运动.

... 粒子群优化(Particle swarm optimization,PSO)算法是一种较新的群智能优化算法,可以对各种连续和离散问题的参数进行寻优操作,具有精度高、收敛快的特点,在目标跟踪^[11]、参数辨识^[12]、信号处理^[13]等领域有较好的应用 ...

2015

0.0

. 2015, 41(9):1722-1728 DOI:doi:10.13700/j.bh.1001-5965.2014.0693

Identification of time-varying systems using multi-scale radial basis function

基于多尺度径向基函数的时变系统辨识

Liu Qing , Li Yang.

刘青, 李阳

A time-varying autoregressive model with time-varying coefficients was investigated to identify linear system parameters from nonstationary time series. The basis function of multi-scale radial basis function (MRBF) was employed, and the identification of nonstationary modeling problem was then simplified to a linear time-invariant modeling problem. Particle swarm optimization (PSO) algorithm was applied to search the optimal RBF scales for the estimation of time-varying system parameters. The basis functions of RBF can better estimate time-varying parameters with a variety of dynamic process because optimal different RBF scales with good local properties can be effectively adjusted by the PSO algorithm. One simulation example of second-order time-varying autoregressive model with time-varying parameters involved different waveform was presented to show the effectiveness of the proposed method. Compared with classical approaches of time-varying parametric estimations such as recursive least square algorithms and the expansion approach of Legendre polynomial basis function, the identification results of time-varying parameters can be more accurately estimated which validates the effectiveness of the proposed time-varying modeling method.

应用非平稳时间序列的时变系统建模方法进行了参数随时间变化的线性系统参数的辨识.通过引入多尺度径向基函数(MRBF)将非平稳过程的辨识问题转化为线性时不变过程的辨识,结合粒子群优化算法(PSO)获得时变系统参数估计的最优径向基函数(RBF)尺度.由于RBF具有良好的局部特性且尺度可以调整,采用RBF作为基函数可以更好地识别具有多种动态过程的时变系统参数.通过对时变系数包含多种波形的二阶时变自回归模型进行仿真辨识,与采用传统的递推最小二乘法和勒让德多项式作为基函数展开式方法相比,提出的方法对于时变系统参数具有更好的跟踪能力,验证了辨识方法的有效性.

2009

0.0

1995

0.0

... 1 基本粒子群优化算法PSO算法^[14]是一种经典的群智能算法,由以下4部分构成:①初始化 ...

2008

0.0

... (1)局部极值问题:算法迭代时,所有粒子都向当前最优解移动,种群搜索空间不断缩小,形成粒子种群快速趋同效应^[15],但是此时的最优位置可能只是某一局部搜索空间里的最优位置,搜索陷入局部极值之中,导致早熟收敛,失去粒子之间所需要保持的多样性 ...