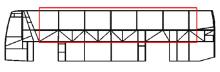
为研究方便, 本文选取一12 m全承载式公路客车侧围上部的一段典型结构为研究对象, 所选取的局部结构包括粘接式车窗玻璃及车身骨架, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 客车侧围典型结构Fig.1 Typical structure of bus side wall

由于整车侧围结构尺寸较大, 为保证后期研究效率^[5], 本文根据原有结构建立了一个简化的缩小比例模型, 并将该模型作为试验和研究的载体。简化比例模型呈悬臂梁结构, 悬臂部分长度和宽度分别为2500 mm和300 mm, 悬臂下沿距离固定端的垂直高度为650 mm。简化模型中包含4个相同尺寸的窗框结构, 每个窗框的尺寸为500 mm× 300 mm。在靠近固定端的两个小窗框处粘接两块钢化玻璃, 玻璃的尺寸为495 mm× 270 mm。以实体单元模拟粘接胶, 以壳单元模拟车身骨架及车窗玻璃(以下简称为壳-体)模型, 单元尺寸确定为1.5 mm。粘接剂选用Terostat8597, 粘接宽度为16.5 mm, 参考客车企业中车窗粘接剂的厚度标准, 本文中粘接厚度取3 mm。窗框采用20号钢焊接而成, 窗框横梁采用30 mm× 40 mm× 1.5 mm的方钢; 窗框短竖梁采用30 mm× 30 mm× 1.5 mm的方钢; 固定端支架采用40 mm× 40 mm× 1.5 mm的方钢。模型所需材料参数如表1所示。

表1

Table 1

表1(Table 1)

表1 材料参数 Table 1 Material parameters 弹性模量/MPa 密度/(g· cm-3) 泊松比 20#钢 206 000 7.8 0.30 粘接剂 2.7 1.2 0.46 钢化玻璃 72 000 2.5 0.20

表1 材料参数 Table 1 Material parameters

添加边界条件时, 在模型右端下部分别约束 A、B两点6个方向的自由度, 在左端分别施加300、400 N的竖直向下的集中载荷。壳-体模型的具体结构及边界条件如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 壳-体模型结构及边界条件Fig.2 Shell-solid model structure and boundary conditions

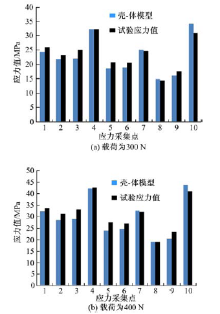
本文建立了简化模型试件以进行静态力学试验^[6], 试验中, 加载和约束情况不变, 获得试验模型10个应力测量点的试验应力值。通过将获得的试验应力值与壳-体模型上相对应的应力采集点的仿真计算应力值进行对比, 验证壳-体模型的正确性。所选取的应力测量点的位置如图3所示。试验现场如图4所示。图5为试验应力值与壳-体模型计算应力值的对比情况。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 试验应力测量点示意图Fig.3 Sketch map of stress measuring points

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 试验现场Fig.4 Testing site

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同载荷下试验与壳-体模型应力值对比Fig.5 Stress comparison under different loads

由图5可知, 壳-体模型的计算应力值与试验应力值最高相差13.03%, 因此认为以实体单元模拟粘接胶的客车粘接式车窗壳-体模型正确且有效。

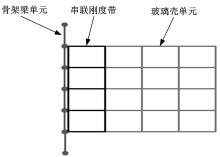
在建立参数化串联刚度模型时, 车身骨架以梁单元模拟, 车窗玻璃以壳单元模拟, 将车窗玻璃与粘接剂相接触的位置定义为串联刚度带, 串联刚度带采用单排壳单元模拟。以串联刚度带来反映车窗玻璃和粘接剂的共同作用效果, 并通过串联刚度带的刚度值变化近似模拟出粘接剂的弹性连接作用。参数化串联刚度模型的简化示意图如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 参数化串联刚度模型简化示意图Fig.6 Sketch map of parameterization series-stiffness model

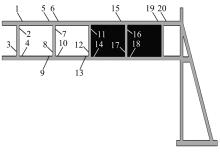
通过设计参数法确定串联刚度带的等效弹性模量时, 需要先获得壳-体模型上的一些点的应力值作为目标应力值。本文随机选取20个应力值较高的非应力集中位置作为应力采集点, 壳-体模型及应力采集点位置如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 壳-体模型及应力采集点位置示意图Fig.7 Sketch map of shell-solid model and locations of stress measuring points

需要确定的串联刚度带的主要参数包括密度、泊松比以及弹性模量。考虑到串联刚度带的质量占模型总质量的比例很小, 且串联刚度带的主要作用是柔性连接车窗玻璃与窗框骨架, 因此以粘接剂的密度和泊松比的值定义串联刚度带的密度和泊松比, 即串联刚度带的密度为1.2 g/cm³, 泊松比为0.46。弹性模量主要影响串联刚度带的刚度特性, 可以通过设计参数法求得。

参照文献^[7]先假定等效弹性模量的值进行计算。将粘接式车窗壳-体模型上的20个应力采集点在300、350、400 N三种加载工况下的应力值组成的应力矩阵 A作为目标应力矩阵。将应用串联刚度法建立的简化模型上的20个应力采集点在3种工况下的应力值组成的应力矩阵定义为B_k。确定一个最优的等效弹性模量使得串联刚度模型的应力结果与壳-体模型的应力计算结果最接近, 即令应力矩阵 Bk与目标应力矩阵 A的偏差最小, 这时对应的等效弹性模量即为该串联刚度模型的最优等效弹性模量。

对壳-体模型左端依次施加300、350及400 N的载荷, 同时计算出壳-体模型上的20个应力采集点在3种载荷下的的应力值 σi,并将其作为目标应力值, 由 σi组成目标应力矩阵 A。应力计算结果如表2所示。

表2

Table 2

表2(Table 2)

表2 壳-体模型应力计算值 Table 2 Calculated stress value of shell-solid model 应力采集点 不同加载工况下应力值/MPa 300 N 350 N 400 N 1 19.25 22.32 25.38 2 8.38 9.71 11.04 3 11.91 13.83 15.75 4 22.55 26.13 29.71 5 20.64 23.95 27.26 6 12.35 14.17 16.00 7 14.21 16.43 18.64 8 14.71 17.01 19.30 9 14.95 17.35 19.75 10 25.41 29.29 33.17 11 12.40 14.25 16.10 12 12.71 14.61 16.50 13 15.17 17.49 19.81 14 19.74 22.63 25.51 15 25.18 28.95 32.72 16 10.35 11.77 13.19 17 10.27 11.68 13.09 18 26.42 30.10 33.78 19 32.47 37.08 41.69 20 13.67 15.85 18.02

表2 壳-体模型应力计算值 Table 2 Calculated stress value of shell-solid model

在获得该串联刚度带的等效弹性模量时, 其等效弹性模量的取值范围是一定的。参考力学中弹簧的串联刚度的定义^[8], 将粘接剂的刚度设为K₁, 车窗玻璃的刚度设为K₂, 则本文所定义的串联刚度带的刚度为K为:

1K=1K1+1K21

由该定义式可知:K介于K₁ 、K₂大小之间。通过该关系可以得到串联刚度带等效弹性模量的上、下限, 上限为车窗玻璃的弹性模量(7.2× 10¹⁰ Pa), 下限为粘接胶的弹性模量(2.7× 10⁶ Pa)。在此范围内取不同的等效弹性模量带入串联刚度模型, 计算获得相应的应力矩阵B_k。由于车窗玻璃的弹性模量远大于粘接胶的弹性模量, 即 K1≪K2, 可以推得:

K=K1K2K1+K2≈K1K2K2=K12

可知串联刚度带的刚度主要受粘接胶的刚度影响, 即串联刚度带的等效弹性模量更贴近粘接胶的弹性模量值。因此, 本文中选择了8组不同的等效弹性模量取值点, 分别为:5、10、15、20、25、30、35、40 MPa(等效弹性模量5、10、15、20、25、30、35、40 MPa下对应的应力矩阵分别为B₁ 、B₂ 、…、B₈)。

为便于衡量应力矩阵 Bk与目标应力矩阵A的偏差, 本文定义应力总偏差 Mk, 以Mk的值作为衡量串联刚度模型偏差的标准。其表达式为:

Mk=∑i=120∑j=13Ai, j-Bki, j23k=1, 2, …, 8

应力总偏差 Mk值最小时所对应的弹性模量即为最优等效弹性模量。如图8所示,

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 10 mm单元串联刚度模型应力总偏差曲线Fig.8 Stress total deviation curve of 10 mm element series-stiffness model

定义串联刚度模型的等效弹性模量为自变量, 应力总偏差 Mk为因变量, 通过最小二乘法^[9]拟合出应力总偏差曲线。

从图8中可以得出:串联刚度模型上的20个应力采集点在3种工况下的应力总偏差最小为12.07 MPa, 此时对应的等效弹性模量为12.48 MPa。将这一等效弹性模量的数值作为10 mm单元尺寸串联刚度模型串联刚度带的最优等效弹性模量。

为实现参数化, 在上文所建立的10 mm单元尺寸串联刚度模型的基础上, 增加5、20以及40 mm单元尺寸的串联刚度模型, 分析得到20个应力采集点的计算应力值, 分别拟合应力偏差曲线, 进而得到3种单元尺寸模型各自所对应的最优等效弹性模量, 如表3所示。

表3

Table 3

表3(Table 3)

表3 不同单元尺寸模型的最优等效弹性模量 Table 3 Optimum equivalent elastic modulus of different element sizes of models 单元尺寸/mm 最小应力总偏差/MPa 最优等效弹性模量/MPa 5 14.58 9.49 10 12.07 12.48 20 11.28 26.31 40 9.56 63.14

表3 不同单元尺寸模型的最优等效弹性模量 Table 3 Optimum equivalent elastic modulus of different element sizes of models

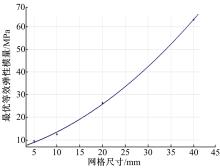
由表3中的数据拟合出单元尺寸-最优等效弹性模量曲线, 如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 单元尺寸-最优等效弹性模量曲线Fig.9 Curve of element size and optimum equivalent elastic modulus

该曲线的函数表达式为:

y=0.02126x2+0.5946x+5.412(4)

利用该曲线, 可以在模型单元尺寸发生改变时, 根据具体的单元尺寸大小找到所对应的串联刚度带的最优等效弹性模量, 实现粘接式车窗玻璃串联刚度模型的参数化建立, 简化建模过程。