交叉口可变导向车道控制优化模型

引用本文

姚荣涵, 张晓彤, 廉莲. 交叉口可变导向车道控制优化模型. 2017, 47(4): 1048-1054
YAO Rong-han, ZHANG Xiao-tong, LIAN Lian. Optimization model for controlling reversible approach lanes at signalized intersections. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1048-1054 复制到剪切板

Permissions

交叉口可变导向车道控制优化模型

姚荣涵, 张晓彤, 廉莲

大连理工大学交通运输学院,辽宁大连 116024

作者简介:姚荣涵(1979-),女,副教授,博士.研究方向:间断交通流理论与方法.E-mail:cyanyrh@dlut.edu.cn

基金:国家自然科学基金项目(51578111).

摘要

为了均衡交通流向分布且保证控制方案平稳过渡,提出具有可变导向车道的交叉口时空资源优化模型以及可变导向车道标志与信号灯组协调控制方法。为验证本文模型与方法的有效性,借助数学软件MATLAB、交通仿真软件VISSIM及其信号控制逻辑工具VisVAP,使用一个算例对比分析可变导向车道控制方案与固定导向车道控制方案。结果表明:与固定导向车道控制方案相比,可变导向车道控制方案使具有可变导向车道的进口道及交叉口的车均延误分别降低3%~50%和7%~15%,说明可变导向车道控制优化模型能适应交叉口交通需求的潮汐特性,可变导向车道标志与信号灯组协调控制方法能保证交通流安全、平稳运行。

关键词: 交通运输系统工程; 单点交叉口; 可变导向车道; 优化模型; 协调控制

中图分类号:U491.4 文献标志码:A 文章编号:1671-5497(2017)04-1048-07

Optimization model for controlling reversible approach lanes at signalized intersections

YAO Rong-han, ZHANG Xiao-tong, LIAN Lian

School of Transportation and Logistics, Dalian University of Technology, Dalian 116024, China

Abstract

To balance directional distribution of traffic flow and ensure the smooth transition of control scenario, an optimization model of time-space resource allocation at an intersection with reversible approach lanes and a coordinated control method for a reversible approach lane and corresponding signal group are proposed. To validate the effectiveness of the optimization model and control method, a case study is carried out to analyze the control scenarios with reversible approach lanes and with fixed approach lanes. The software MATLAB, traffic simulation software VISSIM and the signal control logic tool VisVAP are used in this study. Results show that, comparing to the control scenario with fixed approach lane, the average delay can be reduced by 3% ~ 50% and 7% ~ 15% for the approach with reversible lane and the entire intersection, respectively. The achievements indicate that the proposed optimization model can satisfy the tidal traffic demands at intersections and the control method can guarantee the safe and steady traffic flow operation.

Keyword: engineering of communications and transportation system; isolated intersections; reversible approach lanes; optimization models; coordinated control

Show Figures

0 引言

目前, 国内外关于可变导向车道的研究主要集中于两方面:①可变导向车道控制方法。李丽丽等^[1]提出了基于检测器数据的可变导向车道控制方法, 并对比了可变导向车道功能变化前、后直行车流和左转车流的车均延误。周洋等^[2]研究了检测器的布设, 并明确了可变导向车道功能切换的实施条件和时刻。针对可变导向车道功能发生变化, 陈东静等^[3]提出了主预信号协调控制方法, 并使用VISSIM软件对比了预信号不同时车流的运行效果; ②车道功能动态划分方法。Wong等^[4]从数学建模角度整合了车道功能和信号配时两种设计, 并使用算例说明了交叉口进出口道车道布局的优化问题。为充分利用信号控制交叉口时空资源, Wong等^[5]和He等^[6]先后针对单时段和多时段建立了车道功能和信号相位组合优化模型。

鉴于此, 课题组前期提出了渠化可变导向车道交叉口预设信号配时优化模型, 但没有考虑左转短车道的影响, 也未提出车道功能切换时的具体控制方法^[7]。本文据此完善已有信号配时优化模型, 并提出可变导向车道标志控制方法。

1 信号配时优化模型

1.1 基本假设

在交叉口, 当交通流向具有明显潮汐特性时, 设置可变导向车道能使进口道流量在各条车道上的分布达到均衡。这里探讨可变导向车道功能在左转和直行之间切换。为了便于区分和理解, 将交叉口进口道分为3类:①车道功能随交通需求发生变化的车道称为可变导向车道; ②限于地形条件采用增辟方式形成的固定导向车道称为短车道; ③由路段自然延伸形成的固定导向车道称为普通车道。

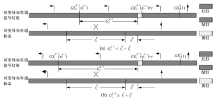
以图1(a)所示进口道为例, 由内到外分别渠化左转短车道、左转专用车道、可变导向车道和直右混行车道各1条。假设该进口道的右转车流不受单独的信号控制, 由于可变导向车道功能为直行或左转, 其相位方案如图1(b)所示, 即左转相位和直右相位。就交叉口而言, 相位相序方案需要考虑所有进口道各股车流之间的关系。

	Figure Option View Download New Window
	图1 进口道渠化方案与相位方案Fig.1 Scenarios of approach layout and signal phasing

1.2 优化模型

考虑可变导向车道与左转短车道对进口道通行能力的影响, 一条车道组的通行能力为:

$\begin{matrix} \begin{matrix} Q_{j} = \\ \{\begin{matrix} \frac{1}{C} [({S^{N}}_{j} + ψ_{j} {S^{V}}_{j}) g_{j} + φ_{j} {S^{S}}_{j} D_{j} \frac{\bar{h}}{\bar{s}}], g_{j} \geq \frac{\bar{h}}{\bar{s}} D_{j} \\ \frac{1}{C} ({S^{N}}_{j} + ψ_{j} {S^{V}}_{j} + φ_{j} {S^{S}}_{j}) g_{j}, g_{j} < \frac{\bar{h}}{\bar{s}} D_{j} \end{matrix} (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} Q_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的通行能力, pcu/h; $\begin{matrix} C \end{matrix}$ 为周期时长, C= $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix} \begin{matrix} g_{i}^{p} \end{matrix}$ +n_dl, s; $\begin{matrix} n \end{matrix}$ 为相位数; $\begin{matrix} {g^{p}}_{i} \end{matrix}$ 为相位 $\begin{matrix} i \end{matrix}$ 的有效绿灯时间, s; $\begin{matrix} n_{d} \end{matrix}$ 为独立相位数; $\begin{matrix} l \end{matrix}$ 为平均相位损失时间, s; $\begin{matrix} {S^{N}}_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的普通车道饱和流率, pcu/h; $\begin{matrix} g_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的有效绿灯时间, g_j= $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ ϕ _ij $\begin{matrix} g_{i}^{p} \end{matrix}$ , s; $\begin{matrix} ϕ_{ij} \end{matrix}$ 为标识车道组 $\begin{matrix} j \end{matrix}$ 上的车流是否在相位 $\begin{matrix} i \end{matrix}$ 内通行的二元变量, 如果是, $\begin{matrix} ϕ_{ij} = 1, \end{matrix}$ 否则, $\begin{matrix} ϕ_{ij} = 0; ψ_{j} \end{matrix}$ 为标识车道组 $\begin{matrix} j \end{matrix}$ 是否含有可变导向车道的二元变量, 如果是, $\begin{matrix} ψ_{j} = 1, \end{matrix}$ 否则, $\begin{matrix} ψ_{j} = 0; {S^{V}}_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的可变导向车道饱和流率, pcu/h; $\begin{matrix} φ_{j} \end{matrix}$ 为标识车道组 $\begin{matrix} j \end{matrix}$ 是否含有短车道的二元变量, 如果是, $\begin{matrix} φ_{j} = 1, \end{matrix}$ 否则, $\begin{matrix} φ_{j} = 0; {S^{S}}_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的短车道饱和流率, pcu/h; $\begin{matrix} D_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的短车道长度, m; $\begin{matrix} \bar{h} \end{matrix}$ 为平均饱和车头时距, s; $\begin{matrix} \bar{s} \end{matrix}$ 为平均停车间距, m。

通过集计可得交叉口通行能力为:

$\begin{matrix} TQ = \overset{m}{\sum_{j = 1}} Q_{j} (2) \end{matrix}$

式中: $\begin{matrix} TQ \end{matrix}$ 为交叉口通行能力, pcu/h; $\begin{matrix} m \end{matrix}$ 为车道组数。

根据美国道路通行能力手册(HCM2000)^[8], 一条进口车道或车道组的车均延误为:

$\begin{matrix} \{\begin{matrix} d_{j} = d_{1 j} (PF) + d_{2 j} + d_{3 j} \\ d_{1 j} = \frac{C (1 - u_{j})^{2}}{2 [1 - \min (1, x_{j}) u_{j}]} \\ d_{2 j} = 900 T [(x_{j} - 1) + \sqrt[]{(x_{j} {- 1)}^{2} + \frac{8 KI x_{j}}{Q_{j} T}}] \\ d_{3 j} = \frac{1800 Q_{b} (1 + μ) t'}{Q_{j} T} \end{matrix} (3) \end{matrix}$

式中: $\begin{matrix} d_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的车均延误, s/pcu; $\begin{matrix} d_{1 j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的均衡延误, s/pcu; $\begin{matrix} u_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的绿信比; $\begin{matrix} x_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的饱和度; $\begin{matrix} PF \end{matrix}$ 为信号联动修正系数; $\begin{matrix} d_{2 j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的增量延误, s/pcu; $\begin{matrix} T \end{matrix}$ 为分析期持续时间, h; $\begin{matrix} K \end{matrix}$ 为信号控制类型的延误修正系数; $\begin{matrix} I \end{matrix}$ 为上游调节增量延误修正系数; $\begin{matrix} d_{3 j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的初始排队延误, s/pcu; $\begin{matrix} Q_{b} \end{matrix}$ 为分析期开始时的排队车辆数, pcu; $\begin{matrix} μ \end{matrix}$ 为延误参数; $\begin{matrix} t' \end{matrix}$ 为分析期内过饱和状态的持续时间, h。

通过集计可得交叉口车辆总延误为:

$\begin{matrix} TD = \overset{m}{\sum_{j = 1}} d_{j} q_{j} T (4) \end{matrix}$

式中: $\begin{matrix} TD \end{matrix}$ 为分析期内交叉口的车辆总延误, s; $\begin{matrix} q_{j} \end{matrix}$ 为车道组 $\begin{matrix} j \end{matrix}$ 的需求流率, pcu/h。

为保障交通流运行安全, 车道组有效绿灯时间应大于或等于最小有效绿灯时间, 即:

$\begin{matrix} \overset{n}{\sum_{i = 1}} ϕ_{ij} {g^{p}}_{i} \geq g_{\min} (5) \end{matrix}$

式中: $\begin{matrix} g_{mi n} \end{matrix}$ 为最小有效绿灯时间, s。

根据信号配时设计理论, 所有相位有效绿灯时间之和加上总损失时间等于周期时长, 其值介于合理的上、下限之间, 即:

$\begin{matrix} C_{\min} \leq \overset{n}{\sum_{i = 1}} {g^{p}}_{i} + n_{d} l \leq C_{\max} (6) \end{matrix}$

式中: $\begin{matrix} C_{\min} \end{matrix}$ 和 $\begin{matrix} C_{\max} \end{matrix}$ 分别为最小和最大周期时长, s。

此外, 相位有效绿灯时间为非负数, 即:

$\begin{matrix} {g^{p}}_{i} \geq 0 (7) \end{matrix}$

为降低交叉口车辆总延误, 以最小化式(4)为目标, 以式(5)(6)(7)为约束条件, 可得信号配时优化模型为:

$\begin{matrix} \{\begin{matrix} minTD = \overset{m}{\sum_{j = 1}} d_{j} q_{j} T \\ s . t . 式 (5) ~ (7) \end{matrix} (8) \end{matrix}$

2 可变导向车道标志控制方法

2.1 控制方案切换原则

为保证交通流运行安全, 在任意一个控制方案切换时刻, 如果上一控制方案未执行完整周期, 需执行完整周期后再切换至下一控制方案。因此, 每一个控制方案修正的切换时刻为:

$\begin{matrix} {t^{A}}_{k} = \{\begin{matrix} t_{1} + C^{1} - \mod (t_{1} - t_{0}, C^{1}), k = 1 \\ t_{k} + C^{k} - \mod (t_{k} - {t^{A}}_{k - 1}, C^{k}), k > 1 \end{matrix} (9) \end{matrix}$

式中: $\begin{matrix} {t^{A}}_{k} \end{matrix}$ 为控制方案 $\begin{matrix} k \end{matrix}$ 修正的切换时刻, s; $\begin{matrix} t_{1} \end{matrix}$ 为控制方案 $\begin{matrix} 1 \end{matrix}$ 的切换时刻, s; $\begin{matrix} C^{1} \end{matrix}$ 为控制时段 $\begin{matrix} 1 \end{matrix}$ 的周期时长, s; $\begin{matrix} \mod (x, y) \end{matrix}$ 为 $\begin{matrix} x \end{matrix}$ 除以 $\begin{matrix} y \end{matrix}$ 的余数; $\begin{matrix} t_{0} \end{matrix}$ 为参考零点, s; $\begin{matrix} t_{k} \end{matrix}$ 为控制方案 $\begin{matrix} k \end{matrix}$ 的切换时刻, s; $\begin{matrix} C^{k} \end{matrix}$ 为控制时段 $\begin{matrix} k \end{matrix}$ 的周期时长, s; $\begin{matrix} {t^{A}}_{k - 1} \end{matrix}$ 为控制方案 $\begin{matrix} k - 1 \end{matrix}$ 修正的切换时刻, s。

2.2 可变导向车道标志显示规则

可变导向车道标志是一种指示标志, 其导向箭头随交通需求变化进行调节, 以实时响应交通流的变化。当可变导向车道功能发生变化时, 驾驶员需要一定的反应时间来适应这种改变。为保证安全, 也需要一定时间清空可变导向车道上还未驶离停车线的车辆。根据相邻时段可变导向车道功能是否发生变化, 将可变导向车道标志显示规则分为两类。

(1)可变导向车道功能不变

当本控制时段的可变导向车道功能与上一控制时段相同时, 上一控制时段与本控制时段任意一个信号周期内各种灯色的信号灯直接按其控制方案起亮和结束, 可变导向车道标志的导向箭头与信号灯组指示方向一致, 且一直高亮显示。

(2)可变导向车道功能改变

当可变导向车道功能发生变化时, 可变导向车道标志的显示规则也要发生变化。为保证控制方案切换时清空上一控制时段可变导向车道上还未驶离停车线的车辆, 并使本控制时段最初进入可变导向车道的车辆顺利驶入, 需计算清空时间和进入时间。

根据交通流的到达与释放规律, 清空时间与进入时间可分别表达为:

${t^{V}}_{ζ} = \{\begin{matrix} \bar{h} {D^{V}}_{ζ} / \bar{s}, \mod (\bar{h} {D^{V}}_{ζ}, \bar{s}) = 0 \\ int (\bar{h} {D^{V}}_{ζ} / \bar{s}) + 1, \mod (\bar{h} {D^{V}}_{ζ}, \bar{s}) \neq 0 \end{matrix} (10)$

$\begin{matrix} \begin{matrix} {t^{E}}_{ζ} = \{\begin{matrix} {D^{V}}_{ζ} / {v^{E}}_{ζ}, \mod ({D^{V}}_{ζ}, {v^{E}}_{ζ}) = 0 \\ int ({D^{V}}_{ζ} / {v^{E}}_{ζ}) + 1, \mod ({D^{V}}_{ζ}, {v^{E}}_{ζ}) \neq 0 \end{matrix} (11) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {t^{V}}_{ζ} \end{matrix}$ 为清空可变导向车道 $\begin{matrix} ζ \end{matrix}$ 上的滞留车辆所需的时间(简称清空时间), s; $\begin{matrix} {D^{V}}_{ζ} \end{matrix}$ 为可变导向车道 $\begin{matrix} ζ \end{matrix}$ 的清空距离, 即停车线后方第1块可变导向车道标志与停车线之间的距离, m; $\begin{matrix} int (x) \end{matrix}$ 为对 $\begin{matrix} x \end{matrix}$ 取整; $\begin{matrix} {t^{E}}_{ζ} \end{matrix}$ 为车辆以进入速度驶过可变导向车道 $\begin{matrix} ζ \end{matrix}$ 的清空距离所需的时间(简称进入时间), s; $\begin{matrix} {v^{E}}_{ζ} \end{matrix}$ 为车辆驶入可变导向车道 $\begin{matrix} ζ \end{matrix}$ 的平均速度(简称进入速度), km/h。

记 $\begin{matrix} G S_{ζ}^{k - 1} (n_{c}^{k - 1}) \end{matrix}$ 和 $\begin{matrix} G E_{ζ}^{k - 1} (n_{c}^{k - 1}) + y \end{matrix}$ 分别为可变导向车道 $\begin{matrix} ζ \end{matrix}$ 信号灯组最后一次执行控制方案 $\begin{matrix} k - 1 \end{matrix}$ 的绿灯和红灯起亮时刻, s; $\begin{matrix} G_{ζ}^{k - 1} \end{matrix}$ 为控制时段 $\begin{matrix} k - 1 \end{matrix}$ 可变导向车道 $\begin{matrix} ζ \end{matrix}$ 信号灯组的绿灯显示时间, s; $\begin{matrix} G S_{ζ}^{k} (1) \end{matrix}$ 为可变导向车道 $\begin{matrix} ζ \end{matrix}$ 信号灯组第1次执行控制方案 $\begin{matrix} k \end{matrix}$ 的绿灯起亮时刻, s。以可变导向车道 $\begin{matrix} ζ \end{matrix}$ 功能由左转切换至直行为例, 若 $\begin{matrix} G_{ζ}^{k - 1} < {t^{V}}_{ζ} + {t^{E}}_{ζ}, \end{matrix}$ 可变导向车道 $\begin{matrix} ζ \end{matrix}$ 标志与信号灯组协调控制关系见图2(a); 若 $\begin{matrix} G_{ζ}^{k - 1} \geq {t^{V}}_{ζ} + {t^{E}}_{ζ}, \end{matrix}$ 相应协调控制关系见图2(b)。

	Figure Option View Download New Window
	图2 可变导向车道功能改变时标志与信号灯组控制状态Fig.2 States of signal group and traffic sign for changing function of a reversible approach lane

3 算例验证

3.1 算例说明

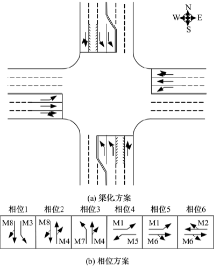
图3给出了一个含可变导向车道交叉口的渠化方案与信号相位方案。

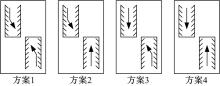
	Figure Option View Download New Window
	图3 交叉口渠化方案与信号相位方案Fig.3 Scenarios of intersection layout and signal phasing

如图3(a)所示, 该交叉口东、西进口道分别渠化1条左转专用车道、直行车道和直右车道, 南、北进口道分别渠化1条左转短车道、左转专用车道、可变导向车道和直右车道。如图3(b)所示, 南、北进口道采用前置左转+后置左转方式, 东、西方向采用专用左转+前置左转方式, 其中M1、M3、M5和M7分别为西、北、东、南进口道的左转车流, M2、M4、M6和M8分别为东、南、西、北进口道的右车流。假定该交叉口交通流组成为100%的小汽车, 图4给出了各股车流的最高15 min流率和小时流量, 图中斜线左侧为最高15 min流率、右侧为小时流量, 单位均为pcu/h。针对图3所示交叉口, 可变导向车道功能属性集包含图5所示的4种方案。

	Figure Option View Download New Window
	图4 小时流量与最高15 min流率Fig.4 Hourly volumes and peak 15 min flow rates

3.2 参数标定

根据HCM2000^[8], 取 $\begin{matrix} C_{\min} = 60 s 、 C_{\max} = 150 s; \end{matrix}$ 假设交叉口交通流随机到达, 并采用单点预设信号控制, 那么PF=1、I=1、K=0.5、Q_b=0pcu。根据文献^[9], 左转车道和直右车道饱和流率均设为1810 pcu/h, 直行车道饱和流率设为1850 pcu/h。根据德国交通信号控制规范^[10], 取 $\begin{matrix} g_{\min} = 10 s 。 \end{matrix}$ 根据文献^[11], 令 $\begin{matrix} l = 3 s 、 \bar{h} = 2 s 、 \bar{s} = 6 m 。 \end{matrix}$ 此外, 设D_j=50m、T=1h、v^E_ζ=50km/h。

	Figure Option View Download New Window
	图5 可变导向车道功能方案Fig.5 Scenarios of functions of reversible approach lanes

使用VISSIM 6.0软件建立交通仿真模型^[12], 机动车期望速度取48~58 km/h; 车辆消失前等待时间取45 s; 黄灯和全红时间分别取3 s和2 s。为拟合饱和流率, 针对左转、直行和直右车道, 安全距离的附加部分取2.45、2.40和2.45, 安全距离的倍数部分取3.45、3.40和3.45^[12]。为消除随机因素, 采用多步运行模式, 仿真次数为5, 仿真时间设为11 400 s, 数据采集时段为600~11 400 s。获取延误数据时, 起始和结束检测断面的间距取200 m。另外, 可变导向车道标志距离停车线50 m。

3.3 结果分析

当可变导向车道功能在所有时段内不发生变化时, 整个信号控制方案被称为固定导向车道控制方案; 反之, 被称为可变导向车道控制方案。当可变导向车道功能采用图5中的方案1、2、3和4时, 其信号控制方案分别被称为固定导向车道控制方案1、2、3和4。

针对上述5种信号控制方案, 使用模型(8)分别对其进行求解, 优化结果见表1。由该表可见, 每个时段内, 可变导向车道控制方案均选择固定导向车道控制方案中最好的一种。因此, 相比固定导向车道控制方案, 可变导向车道控制方案能使交通流始终处于最佳运行状态。

	Figure Option View Download New Window
	图6 不同信号控制方案下车均延误的对比Fig.6 Comparisons of unit delay under different signal control schemes

表1 不同信号控制方案的优化结果 Table 1 Optimization results of different signal control schemes

针对可变导向车道控制方案, 由式(10)和(11)计算得到可变导向车道的清空时间和进入时间分别为17 s和4 s。

对于每种信号控制方案, 通过运行VISSIM仿真模型获取整个控制时段各进口道及交叉口的车均延误, 其对比结果如图6所示。从图6可以看出, 与固定导向车道控制方案相比, 可变导向车道控制方案使南进口道车均延误降低13.72%~47.25%、北进口道车均延误降低3.46%~50.34%, 而东、西进口道的车均延误可能有不同程度的增加, 就整个交叉口而言, 车均延误降低7.39%~14.62%。

4 结束语

面向渠化可变导向车道和左转短车道的信号控制交叉口, 以最小化车辆总延误为目标, 以可变导向车道功能和相位有效绿灯时间为决策变量, 构建了一种具有可变导向车道的交叉口时空资源优化模型; 进一步提出了可变导向车道标志与信号灯组协调控制方法。为了说明本文模型和方法的可行性, 设计了一个具有2条可变导向车道的十字交叉口, 以3个控制时段为例, 针对4种固定导向车道控制方案和可变导向车道控制方案, 使用本文模型获得了最优的配时参数和性能指标, 并利用VISSIM软件建立了交通流仿真模型。此外, 采用信号控制逻辑工具VisVAP实现了可变导向车道控制。结果显示, 可变导向车道控制方案在每个控制时段内均不劣于任意一种固定导向车道控制方案, 该方案可以明显降低具有可变导向车道的进口道以及整个交叉口的车均延误。这说明本文模型和方法能够很好地适应交叉口交通流向的潮汐特性, 并保证交通流安全、平稳地运行。研究成果可以为相关的工程实践提供理论依据, 并有助于缓解城市交通拥堵。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李丽丽, 曲昭伟, 陈永恒, 等. 可变车道的控制方法[J]. 吉林大学学报: 工学版, 2009, 39(增刊1): 98-103. Li Li-li, Qu Zhao-wei, Chen Yong-heng, et al. Control strategy of variable lane[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(Sup. 1): 98-103. [本文引用:1]
[2]	周洋, 林浩, 顾姗姗, 等. 信号交叉口可变导向车道上游检测器布设及触发条件研究[J]. 北京理工大学学报, 2013, 33(12): 1298-1302. Zhou Yang, Lin Hao, Gu Shan-shan, et al. Detector layouts and trigger conditions of upstream variable lanes at signalized intersections[J]. Transactions of Beijing Institute of Technology, 2013, 33(12): 1298-1302. [本文引用:1]
[3]	陈东静, 李林波, 朱锐, 等. 信号交叉口可变车道主预信号配时协调关系研究[J]. 重庆交通大学学报: 自然科学版, 2013, 32(2): 252-257. Chen Dong-jing, Li Lin-bo, Zhu Rui, et al. Coordinate relationship between main signals and pre-signals of the variable lane at signalized intersection[J]. Journal of Chongqing Jiaotong University (Natural Science), 2013, 32(2): 252-257. [本文引用:1]
[4]	Wong C K, Heydecker B G. Optimal allocation of turns to lanes at an isolated signal-controlled junction[J]. Transportation Research Part B: Methodological, 2011, 45(4): 667-681. [本文引用:1]
[5]	Wong C K, Wong S C, Tong C O. A lane-based optimization method for the multi-period analysis of isolated signal-controlled junctions[J]. Transportmetrica, 2006, 2(1): 53-85. [本文引用:1]
[6]	He S, Wang W, Zhang J, et al. An improved optimization method for isolated signalized intersection based on the temporal and spatial resources integration[J]. Procedia-Social and Behavioral Sciences, 2013, 96: 1696-1706. [本文引用:1]
[7]	李丽丽, 姚荣涵, 周红媚, 等. 渠化可变导向车道交叉口预设信号配时优化模型[J]. 吉林大学学报: 工学版, 2015, 45(1): 75-81. Li Li-li, Yao Rong-han, Zhou Hong-mei, et al. Optimization model for pretimed signals at an intersection with reversible approach lanes[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(1): 75-81. [本文引用:1]
[8]	Transportation Research Board. Highway Capacity Manual (HCM) 2000[R]. Washington DC: National Research Council, 2001. [本文引用:2]
[9]	Akçelik R. Traffic signals: capacity and timing analysis[R]. Research Report No. 123, Vermont South: Australian Road Research Board, 1981. [本文引用:1]
[10]	Road and Transportation Research Association (RTRA). Guidelines for traffic signals (RiLSA)[R]. Cologne: Steering Committee for Traffic Control and Traffic Safety, 2003. [本文引用:1]
[11]	Roess R P, Prassas E S, McShane W R. Traffic Engineering[M]. 3rd ed. Beijing: China Machine Press, 2008. [本文引用:1]
[12]	Planung Transport Verkehr(PTV) AG. PTV VISSIM 6 User Manual[M]. Karlsruhe, Germany: Planung Transport Verkehr (PTV) AG, 2014. [本文引用:2]

2009

0.0

... 李丽丽等^[1]提出了基于检测器数据的可变导向车道控制方法,并对比了可变导向车道功能变化前、后直行车流和左转车流的车均延误 ...

2013

0.0

... 周洋等^[2]研究了检测器的布设,并明确了可变导向车道功能切换的实施条件和时刻 ...

2013

0.0

... 针对可变导向车道功能发生变化,陈东静等^[3]提出了主预信号协调控制方法,并使用VISSIM软件对比了预信号不同时车流的运行效果 ...

2011

0.0

... Wong等^[4]从数学建模角度整合了车道功能和信号配时两种设计,并使用算例说明了交叉口进出口道车道布局的优化问题 ...

2006

0.0

... 为充分利用信号控制交叉口时空资源,Wong等^[5]和He等^[6]先后针对单时段和多时段建立了车道功能和信号相位组合优化模型 ...

2013

0.0

... 为充分利用信号控制交叉口时空资源,Wong等^[5]和He等^[6]先后针对单时段和多时段建立了车道功能和信号相位组合优化模型 ...

2015

0.0

. 2015, 45(1):75-81 DOI:10.13229/j.cnki.jdxbgxb201501012

Optimization model for pretimed signals at an intersection with reversible approach lanes

渠化可变导向车道交叉口预设信号配时优化模型

Li Li-li , Yao Rong-han , Zhou Hong-mei

李丽丽, 姚荣涵, 周红媚

1.Center for Modern Transportation Development Research, Transport Management Institute, Ministry of Transport of the People's Republic of China, Beijing 101601, China; 2.School of Transportation and Logistics, Dalian University of Technology, Dalian 116024, China

To fully utilize the time-space resources of an intersection with reversible approach lanes, an optimization model was developed for pretimed signals. The objective of this model is to minimize the total delay for all vehicles. The decision variables are the function of each reversible approach lane and the effective green time per signal phase. This model was validated by a case using the traffic simulation software VISSIM.The results indicate that there is an optimal combination of the two variables by which the average delay per vehicle for each movement, the average queue length and the maximum queue length on each approach can be minimized. To further consider the multi-period signal control, the procedure of the multi-period pretimed signal timing design for an intersection with reversible approach lanes was proposed. The research achievement can reasonably allocate the function of each reversible approach lane and the signal timing scheme during any time period for a signalized intersection, effectively improving the operation efficiency of traffic flow and providing a theoretical basis and method for the control of reversible approach lanes.

为了充分利用渠化可变导向车道交叉口的时空资源，建立了以交叉口车辆总延误最小为优化目标、以可变导向车道功能和相位有效绿灯时间为决策变量的预设信号配时优化模型。使用交通仿真软件VISSIM对本文模型进行了模拟验证。结果表明，可变导向车道功能和相位有效绿灯时间存在最佳组合，这种组合能使各股车流的车均延误最小、各进口道的平均排队长度和最大排队长度最短。为了进一步考虑多时段信号控制问题，提出了渠化可变导向车道交叉口多时段预设信号配时设计流程。研究成果能够合理地设定信号交叉口任一时段可变导向车道功能与信号配时方案，可以有效地提高交通流运行效率，为可变导向车道控制提供理论依据与方法。

... 鉴于此,课题组前期提出了渠化可变导向车道交叉口预设信号配时优化模型,但没有考虑左转短车道的影响,也未提出车道功能切换时的具体控制方法^[7] ...

2001

0.0

... 根据美国道路通行能力手册(HCM2000)^[8],一条进口车道或车道组的车均延误为: ...

... 2 参数标定根据HCM2000^[8],取 Cmin=60s、Cmax=150s ...

1981

0.0

... 根据文献^[9],左转车道和直右车道饱和流率均设为1810 pcu/h,直行车道饱和流率设为1850 pcu/h ...

2003

0.0

... 根据德国交通信号控制规范^[10],取 gmin=10s ...

2008

0.0

... 根据文献^[11],令 l=3s、h-=2s、s-=6m ...

2014

0.0

... 0软件建立交通仿真模型^[12],机动车期望速度取48~58 km/h ...

... 45^[12] ...