城市群综合运输通道布局优化双层模型

引用本文

姜攀, 杨家其, 房瑞伟. 城市群综合运输通道布局优化双层模型. 2017, 47(4): 1061-1067
JIANG Pan, YANG Jia-qi, FANG Rui-wei. Bi-level programming model for optimization of urban agglomeration comprehensive transportation corridor layout. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1061-1067 复制到剪切板

Permissions

城市群综合运输通道布局优化双层模型

姜攀, 杨家其, 房瑞伟

武汉理工大学交通学院,武汉 430063

通讯作者：杨家其(1964-),男,教授,博士生导师.研究方向:交通运输规划与管理.E-mail:styjq@whut.edu.cn

作者简介:姜攀(1982-),男,讲师,博士研究生.研究方向:综合交通规划.E-mail:20173105@qq.com

基金:国家自然科学基金项目(51279153); 吉林省交通运输厅交通运输科技计划项目(2012-1-17).

摘要

从两个层面对城市群综合运输通道进行分析和建模,一是建设管理的决策部门,二是利用通道出行的个体。决策部门的目标是使通道的社会效益最大化,而个体的目标是广义费用最少,由此本文建立了一个双层规划模型,并提出利用改进型混合编码-多种群遗传算法进行计算求解。长吉图实例分析表明,其优化结果基本符合区域内城市的发展路径,表明本文模型有一定的现实参考意义。

关键词: 交通运输系统工程; 城市群; 双层规划模型; 综合运输; 通道; 布局优化

中图分类号:U491,U113 文献标志码:A 文章编号:1671-5497(2017)04-1061-07

Bi-level programming model for optimization of urban agglomeration comprehensive transportation corridor layout

JIANG Pan, YANG Jia-qi, FANG Rui-wei

School of Transportation, Wuhan University of Technology, Wuhan 430063,China

Abstract

The integrated transport corridor of urban agglomeration is analyzed and modeled from two aspects, the decision-making department of the construction and management, and the individual corridor users. The decision-making department must consider the investment cost, ecological environment, natural resources, energy consumption, economical development, political and national defense as well as construction of the appropriate advance, with the goal to maximize the social benefits of the corridor. The individuals are concerned with the least cost in a broader sense. Considering the concerns of the two aspects, a bi-level programming model is proposed to solve the problem using the improved hybrid coding and Multi-Population Genetic (MPG) algorithm. A case study of Chang-Ji-Tu region is conducted to verify the proposed model. The optimal results are basically in accordance with the development path of these cities in the region, indicating that the proposed model has reference significance.

Keyword: engineering of communication and transportation system; urban agglomeration; bi-level programming model; comprehensive transportation; corridor; layout optimization

Show Figures

0 引言

现有运输通道布局优化研究中, 常见的是以城市交通为对象进行网络优化设计, 或是将各种运输方式和客货运单独分析^{[1, 2, 3, 4]}。以城市群为研究对象的综合运输通道研究并不多见。刘强等^[5]和李艳红等^[6]分别用三层规划模型和多目标决策优化方法对区域综合运输通道进行了研究, 前者未说明模型中的运价与现实中运价制订的关系, 后者并未考虑交通流改变下的网络优化问题。本文首先分析城市群的交通特点, 从综合运输的角度把通道布局优化分成两个层面, 即通道建设管理的决策层和通道使用的运行层, 通过各层的内在要素建立各自模型, 并以客货运流量作为两个模型的联系参数构建了一个双层规划模型。最后采用一种改进型混合编码的多种群遗传算法求解得出通道布局优化的方案, 为合理建设各运输方式下的通道提供理论支持。

1 运输通道布局优化的框架

1.1 城市群综合运输通道

目前, 大多数学者是以城市为对象来研究通道布局, 对于城市群的综合运输通道布局, 应区分两者之间的不同要素, 本文从交通小区划分、路径选择方式、出行时间构成及其交通流特征等3个主要方面进行比较。

(1)交通小区划分。城市范围内的路网小区划分, 是按照一定参照指标分成若干个交通小区, 每个小区作为交通量发生和吸引的出发地和目的地, 在这种交通分配模型中, 所有交通量均认为从一个交通小区的质心点到另一个交通小区的质心点^[7]。但是在进行城市群交通研究时, 为便于数据收集一般按照行政区划分交通小区, 此时交通小区划分时对城市群的小区划分, 其小区面积较大, 导致出发点可能与假设的质心点相隔距离比较远, 从而导致个体在路径选择时, 可能按照拟定好的路径进行, 此时不再适合现有交通分配原则。

(2)路径选择与实际交通量。对城市群运输通道中的公路干道而言, 一方面通道周边可能存在条件比较好的非通道(县道、村村通公路)路径, 出行者有可能会暂时离开通道, 也就是说非通道路线在局部范围内也可分担一部分交通流; 另一方面, 城市群内众多由低等级公路与较高等级公路组成的交通网, 在分析由通道组成的综合运输网络交通分配时, 现实中会很难统计完全可靠的交通流数据。

(3)出行时间构成及其交通流特征。传统的运输配流是在考虑拥挤对出行时间影响的基础上, 以城市道路为研究对象, 而不同时间段内, 上下班高峰小时段的城市交通量与非高峰小时段的交通量差异非常大。而以城市群作为研究对象, 一方面在市际交通通道上没有上下班高峰时段出行引起的大规模道路拥挤现象, 因此可看做匀速行驶计算得出交通量; 另一方面, 城市交通通道上的出行时间则按照实际情况具体分析计算或调研得出。

城市群的交通出行时间以公路、铁路两种客运方式进行说明, 客运方式的交通流并不能直接进入通道, 需要在城区消耗一定的时间(如乘坐长途客车包含出发到客运站的时间、候车时间、客车出城时间), 才能进入通道, 这段市内出行时间长短会影响到通道选择从而改变运输配流结果。

1.2 通道布局优化的流程框架

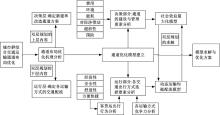
在分析了城市群和城市综合运输通道之间不同的要素后, 本文将通道分为建设管理和使用两个部分, 即通道的决策和运行。决策部门关心的是投资费用、生态环境、自然资源、能源消耗、对经济带动、政治国防以及建设适当超前性等要素。运行部分则关系到个体出行交通方式选择。把通道布局优化从定性分析转化为定量分析, 则需要找出两部分的内在联系要素, 然后构建一个双层规划模型进行计算求解, 根据结果来提供优化方案, 具体的流程如图1所示, 一方面, 个体出行方式选择的改变会导致通道上交通流量的变化, 从而影响决策层的通道布局方案实施; 另一方面, 通道布局优化阶段性完成后反过来又会影响出行方式的选择。出行方式与通道布局之间是通过交通流量来建立关系的。

	Figure Option View Download New Window
	图1 城市群综合运输通道布局优化流程框架Fig.1 Framework for optimization of urban agglomeration comprehensive transportation corridor layout

2 通道布局优化双层规划模型

2.1 模型建立的条件分析

在构建量化模型时, 要素太多往往导致计算量大, 使得求解困难或无法进行。为了解决该问题, 通常采用近似计算, 把一些对求解结果影响不大的要素简化或单独考虑计算。

(1)如表1、表2所示(资料来源于中国统计局《中国统计年鉴》(2015)), 各年客货运量中, 公路、铁路两种运输方式所占比例总和将近98%, 这样在建立模型时, 为了方便求解, 将其他运输方式单独计算优化, 而双层规划中, 只考虑公路和铁路两种运输方式。

表1 2010~2014年各运输方式客运量比较 Table 1 Passenger volume of each transports for years 2010-2014 万人

表2 2010~2014年各运输方式货运量比较 Table 2 Freight volume of each transports for years 2010-2014 万吨

(2)有些通道交通量不大, 但对于国防与防灾具有重要作用, 这部分内容可配合现有通道单列分析。

(3)对于通道改扩建的超前性, 目前无明确指标定义, 本文拟定一个交通量超前系数并指定每隔5年做一次调整, 远景年设为2030年。

(4)机动车噪音和尾气对环境的影响, 政府职能部门并无对应定量拨款治理, 依据噪音和尾气排放来计算环境环保费用并无科学依据。

2.2 模型假设

运输通道的布局优化是个复杂的系统工程, 很多要素错综复杂的叠加在一起, 为此, 本文基于以下假设条件完成对模型的梳理。

(1)在综合运输通道技术等级改造中, 不考虑车道数不同而导致的单位平均改造费用不同。

(2)通道上个体出行符合整体用户出行的广义费用最小。

(3)以技术等级路线作为指标定义公路、铁路通道中各运输方式构成。铁路分为客运专线和一、二级干线; 公路分为高速和一、二级公路。

2.3 模型的建立

上层模型1:本层分析的是通道优化的决策问题。政府决策部门通过分析投资费用、生态环境、自然资源、能源消耗、对经济带动、政治国防以及建设适当超前性等要素, 使得运输系统的社会效益最大。这些要素可分为两类:一种是固定投资; 另一种是随着交通流量改变的总成本(生态环境、自然资源、能源消耗、对经济带动), 后者可归纳为交通运输可持续化发展的广义费用最低。

$minF = \sum_{s \in S} \overset{m}{\sum_{i = 1}} (δ_{s}^{i} L_{s}^{i} x_{s}^{i} X_{s}^{i} + L_{s}^{i} g_{s}^{i} G_{s}^{i}) + \sum_{s \in S} \overset{m}{\sum_{i = 1}} λ_{i} (1 + δ_{s}^{i} X_{s}^{i}) L_{s}^{i} q_{s}^{i} t_{s}^{i} c_{s}^{i} (1)$

$δ_{s}^{i} L_{s}^{i} x_{s}^{i} X_{s}^{i} + L_{s}^{i} g_{s}^{i} G_{s}^{i} \leq C (2)$

$\sum_{s \in S} \overset{m}{\sum_{i = 1}} (1 + δ_{s}^{i} X_{s}^{i}) L_{s}^{i} \leq L (3)$

$s.t. X_{s}^{i}, G_{s}^{i} \in \{0, 1\} (4)$

$\overset{m}{\sum_{i = 1}} q_{s}^{i} = Q_{s} (5)$

$q_{s}^{i} \geq 0 (6)$

式中: $\begin{matrix} s \end{matrix}$ 表示城市群OD内任意一段; $\begin{matrix} i \end{matrix}$ 表示运输方式( $\begin{matrix} i = 1 \end{matrix}$ 为客运专线, $\begin{matrix} i = 2 \end{matrix}$ 为一级干线铁路, $\begin{matrix} i = 3 \end{matrix}$ 为二级干线铁路; $\begin{matrix} i = 4 \end{matrix}$ 为高速公路, $\begin{matrix} i = 5 \end{matrix}$ 为一级公路, $\begin{matrix} i = 6 \end{matrix}$ 为二级公路); $\begin{matrix} λ_{i} \end{matrix}$ 表示运输方式 $\begin{matrix} i \end{matrix}$ 可持续发展的成本系数; $\begin{matrix} \sum_{s \in S} \end{matrix}$ $\begin{matrix} \overset{m}{\sum_{i = 1}} \end{matrix}$ λ _i(1+ $\begin{matrix} δ_{s}^{i} \end{matrix} \begin{matrix} X_{s}^{i} \end{matrix}$ ) $\begin{matrix} L_{s}^{i} \end{matrix} \begin{matrix} q_{s}^{i} \end{matrix} \begin{matrix} t_{s}^{i} \end{matrix} \begin{matrix} c_{s}^{i} \end{matrix}$ 表示综合运输通道下的广义费用; $\begin{matrix} x_{s}^{i} 、 g_{s}^{i} \end{matrix}$ 分别表示OD对 $\begin{matrix} s \end{matrix}$ 间新建和改建成等运输方式 $\begin{matrix} i \end{matrix}$ 的单位费用(未考虑车道数对等级改变的影响, 下同); $\begin{matrix} t_{s}^{i} 、 c_{s}^{i} \end{matrix}$ 分别表示OD对 $\begin{matrix} s \end{matrix}$ 间运输方式 $\begin{matrix} i \end{matrix}$ 的旅行时间和单位平均价格; $\begin{matrix} L_{s}^{i} \end{matrix}$ 为OD对 $\begin{matrix} s \end{matrix}$ 间运输方式 $\begin{matrix} i \end{matrix}$ 原路线的里程; $\begin{matrix} δ_{s}^{i} \end{matrix}$ 为路网的形变系数, OD对 $\begin{matrix} s \end{matrix}$ 间运输方式 $\begin{matrix} i \end{matrix}$ 新建路线与原路线 $\begin{matrix} L_{s}^{i} \end{matrix}$ 的里程比值; $\begin{matrix} X_{s}^{i} \end{matrix}$ 为0-1变量, 在OD对 $\begin{matrix} s \end{matrix}$ 间新建运输方式 $\begin{matrix} i \end{matrix}$ 时, $\begin{matrix} X_{s}^{i} = 1 \end{matrix}$ 表示新建, 不新建则为0; $\begin{matrix} G_{s}^{i} \end{matrix}$ 为0-1变量, 在OD对 $\begin{matrix} s \end{matrix}$ 间改造运输方式 $\begin{matrix} i \end{matrix}$ 时, $\begin{matrix} G_{s}^{i} = 1 \end{matrix}$ 表示改造, 不改造则为0; (对公路通道而言, 本文改造仅指二级升一级, 高速公路无改建, 铁路同理)。

式(1)表达投资费用和综合运输通道可持续发展成本两者之和最小; 约束条件(2)确保投资费用不超过投资总额 $\begin{matrix} C; \end{matrix}$ 约束条件(3)表明优化后的通道总里程不大于规划的总里程; 约束条件(5)保证OD对 $\begin{matrix} s \end{matrix}$ 间的客货流量等于总流量。

下层模型2:本层模型分析的是个体在通道上的出行情况。个体出行路径的选择从整个运输网络上看符合广义费用最小。交通需求会随着运输网络的变化而变化, 研究此类问题时宜使用弹性需求的用户平衡(User equilibrium, UE)模型和随机用户平衡(Stochastic user equilibrium, SUE)模型^{[8, 9]}。个体出行成本是随机的, 且与路径上流量相关时, 路径选择概率则是与流量相关的函数。从综合运输通道的角度分析, 也就是各运输方式分担率随着通道流量的变化而变化。综合交通网络随机配流模型^[5]描述通道内用户的交通选择过程见式(7)。

$minZ (q_{s}^{i}) = \frac{1}{θ} \sum_{s} \overset{m}{\sum_{i = 1}} q_{s}^{i} \ln q_{s}^{i} + \sum_{s \in S} \overset{m}{\sum_{i = 1}} \int_{0}^{q_{s}^{i}} f (w) dw (7)$

$\begin{matrix} \begin{matrix} s . t . \overset{m}{\sum_{i = 1}} q_{s}^{i} = Q_{s}, q_{s}^{i} \geq 0 (8) \\ \forall i = 1, 2, \dots, m, s \in S \end{matrix} \end{matrix}$

式中: $\begin{matrix} θ \end{matrix}$ 是非负校正参数; 函数 $\begin{matrix} f \end{matrix}$ 是以客货流量为自变量关于各运输方式的广义费用函数, 若考虑准点率、安全性、运费、运输时间和发车频率等要素, 其表达如下:

$\begin{matrix} f = P_{i} S_{i} (θ_{1} E_{i} + θ_{2} t_{i} + θ_{3} M_{i}) (9) \end{matrix}$

式中: $\begin{matrix} P_{i} 、 S_{i} 、 E_{i} 、 t_{i} 、 M_{i} \end{matrix}$ 分别为运输方式 $\begin{matrix} i \end{matrix}$ 的准点率、安全性、运费、运输时间、发车频率; $\begin{matrix} θ_{1} 、 θ_{2} 、 θ_{3} \end{matrix}$ 为特性参数。

对于铁路网运输, 出行时间 $\begin{matrix} t \end{matrix}$ 在可依据调查数据给出。对于公路网中通道, 依据美国道路局开发的BPR函数^[10], 运输时间与交通交通量的数学形式为:

$\begin{matrix} t = t_{a} (0) [1 + α {(\frac{q_{s}}{C_{s}})}^{β}] (10) \end{matrix}$

式中: $\begin{matrix} t_{a} (0) \end{matrix}$ 为路段 $\begin{matrix} s \end{matrix}$ 的自由行走时间; $\begin{matrix} C_{s} \end{matrix}$ 为路段 $\begin{matrix} s \end{matrix}$ 的交通容量; $\begin{matrix} q_{s} \end{matrix}$ 为路段 $\begin{matrix} s \end{matrix}$ 的交通量; $\begin{matrix} α 、 β \end{matrix}$ 为参数。

2.4 模型参数设定

路网变形系数:由平原向山区过度取值1.10~1.30, 具体数值。参考中国图们江区域合作开发规划和长吉图开发开放先导区《公路交通发展规划报告》。

可持续发展成本系数 $\begin{matrix} λ : \end{matrix}$ 在交通量一定时, 不同运输方式下的交通量比例构成总成本最小, 通过多目标决策灰色关联度评价法^[11]来确定。

特性参数 $\begin{matrix} θ \end{matrix}$ 的标定:特性参数 $\begin{matrix} θ \end{matrix}$ 表示对运输方式 $\begin{matrix} i \end{matrix}$ 服务属性权重的评价, $\begin{matrix} θ_{1} \end{matrix}$ 表示运输费用的权重, $\begin{matrix} θ_{2} \end{matrix}$ 表示时间快速性的权重, $\begin{matrix} θ_{3} \end{matrix}$ 表示运输方便性的权重, 此类问题的求解可用极大似然法。

运输时间与交通量函数: $\begin{matrix} α = 0.15, β = 4, \end{matrix}$ 均为美国道路局前期的推荐赋值^[10]。

3 模型的算法与求解

城市群综合运输通道布局优化问题中既有针对新建与改建路线等参数设定的0-1型离散整数变量, 又有投资费用、能耗、环境保护成本等构成的连续性变量, 对于此类混合变量类的交通布局组合优化问题, 本文首次提出用改进型混合编码遗传算法进行求解。

改进算法的关键是:在生成初始种群时, 将不同类型的变量进行分类, 将相同类型的变量放在同一元胞内, 这样在操作基因重组(交叉)或变异时, 将不同类型的变量分开进行, 根据需求选择概率, 以便合理控制子代的变化差异范围; 其次, 对于城市群综合运输通道布局优化模型中变量较多, 可行解空间大, 使用传统遗传算法时可能存在未成熟收敛的现象^[12], 本文使用多种群遗传算法。算法的步骤流程如下:

Step1 模型数据初始化。给出初始年中各OD对 $\begin{matrix} s \end{matrix}$ 间的客货运量 $\begin{matrix} q_{s}^{i} \end{matrix}$ 以及 $\begin{matrix} X_{s}^{i} 、 G_{s}^{i} \end{matrix}$ 的初始值, 令迭代次数 $\begin{matrix} j \end{matrix}$ =0。

Step2 求解下层模型。得到最优解 $\begin{matrix} q_{s}^{i} \end{matrix}$ , 计迭代次数 $\begin{matrix} j \end{matrix}$ +1。

Step3 超前性判定。设置通道布局优化超前量μ 。若j=5n, n∈ {1, 2, …}, 赋值 $\begin{matrix} q_{s}^{i} = (1 + μ) q_{s}^{i}; \end{matrix}$ 否则, 直接执行Step4。

Step4 求解上层模型。将客货运流量 $\begin{matrix} q_{s}^{i} \end{matrix}$ 换算为标准客(货)流量后代入上层模型, 得到新的最优解 $\begin{matrix} X_{s}^{i} 、 G_{s}^{i} 。 \end{matrix}$

Step5 循环计算。重复上述步骤。

Step6 收敛判定。设定精度 $\begin{matrix} σ, \end{matrix}$ 当上层模型中 $\begin{matrix} |F^{{j + 1}} - F^{j}| \leq σ \end{matrix}$ 时, 停止循环。

4 长吉图综合运输通道实例分析

本文以武汉理工大学交通学院承担的吉林省交通运输厅《长吉图综合交通运输网评估及优化布局技术》的调研数据为基础, 结合现有通道的抽样调查数据, 进行模型参数的标定。根据经济先进省份运输通道发展模式, 根据国土系数法确定长吉图区域运输网规模, 根据通道在运输网所占比例, 确定未来年的投资总额。

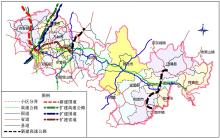
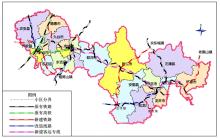
通过将模型分别设定为2015、2020和2030年, 得到不同的建设顺序, 结合未来年的流量分布确定长吉图综合运输通道布局优化的实施方案, 如表3及图2、图3所示。如前文所述, 航空与水运在客货运中运量占比小, 其通道的优化方案是结合吉林省综合交通发展规划后单独考虑各自运输方式下优化得到的, 优化过程从略。

表3 长吉图综合运输网通道优化方案 Table 3 Chang-Ji-Tu optimization scheme of comprehensive transportation corridor

	Figure Option View Download New Window
	图2 公路网通道优化方案(2020~2030年)Fig.2 Optimization scheme of highway corridor

	Figure Option View Download New Window
	图3 铁路网通道优化方案(2020~2030年)Fig.3 Optimization scheme of railway corridor

由优化方案可看出, 通道布局优化集中在经济发展较好的地方, 符合城市发展的特征。通道未来年新建和扩建速度与长吉图近十年发展规模相比较, 明显放慢, 这可能主要与运输结构日益合理且运输通道的通达性越来越好相关。

5 结束语

本文以城市群为对象, 从交通小区划分、路径选择方式、出行时间构成及其交通流特征等3方面分析了出行方式选择的特点, 通过研究城市群综合运输通道布局优化的决策和运行使用两大部分, 建立了一个双层规划模型并提出利用改进型混合编码-多种群遗传算法求解具有复杂的交通布局组合优化问题, 优化过程中结合实际给出了路网变形参数和交通量超前的调节参数, 为现实中的通道优化方案的框架提供了辅助决策依据。长吉图综合运输通道的实例优化结果基本符合区域内城市的发展路径, 表明本文研究结果有一定的现实参考意义。为了让求解模型简单易行, 对部分要素进行了简化并将一些参数设为定量, 如单位建设成本, 单位能耗, 此外维护保养也未考虑。现实中, 由于调研的局限性, 并未对国防通道和重要产业下的通道建设进行分析。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Kashani H R, Saridis G N. Intelligent control for urban traffic systems[J]. Automatic, 1983, 19(2): 191-197. [本文引用:1]
[2]	李友好, 刘晓佳, 施其洲. 基于网络的运输通道客运流量分配模型[J]. 交通运输工程与信息学报, 2005, 3(2): 57-62. Li You-hao, Liu Xiao-jia, Shi Qi-zhou. Trip assignment model for transportation corridor based on network equilibrium[J]. Journal of Transportation Engineering and Information, 2005, 3(2): 57-62. [本文引用:1]
[3]	Guida Michele, Maria Funaro. Topology of the Italian airport network: a scale-free small-world network with a fractal structure[J]. Chaos, Solitons and Fractals, 2007, 31: 527-536. [本文引用:1]
[4]	LeBlanc L J, Boyce D E. A bi-level programming algorithm for exact solution of the network design problem with use optimal flows[J]. Transportation Research, 1986, 20B(3): 259-265. [本文引用:1]
[5]	刘强, 陆化普, 王庆云. 区域运输通道布局优化三层规划模型[J]. 清华大学学报: 自然科学版, 2010, 50(6) : 815-819. Liu Qiang, Lu Hua-pu, Wang Qing-yun. Tri-level programming model for optimization of regional transportation corridor layout[J]. Journal of Tsinghua University (Science and Technology), 2010, 50(6): 815-819. [本文引用:2]
[6]	李艳红, 袁振洲, 陈静云, 等. 基于多目标决策的综合运输通道组合运能优化[J]. 吉林大学学报: 工学报, 2009, 39(6): 1481-1485. Li Yan-hong, Yuan Zhen-zhou, Chen Jing-yun, et al. Combined capacity optimization of comprehensive transportation corridor based on multi-objective decision making[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(6): 1481-1485. [本文引用:1]
[7]	闫小勇, 刘博航. 交通规划软件实验教程[M]. 北京: 机械工业出版社, 2010: 68-71. [本文引用:1]
[8]	Lo H K, Chang E, Chan Y C. Dynamic network traffic control[J]. Transportation Research, 2001, 35A(1): 721-744. [本文引用:1]
[9]	高自友, 张好智, 孙会君. 城市交通网络设计问题中双层规划模型、方法及应用系统工程理论与方法[J]. 系统工程理论与方法, 2004, 4(1): 35-42. Gao Zi-you, Zhang Hao-zhi, Sun Hui-jun. Bi-level programm ing models, approaches and applications in urban transportation network design problems[J]. Journal of Transportation System Engineering and Information Technology, 2004, 4(1): 35-42. [本文引用:1]
[10]	陆化普. 交通规划理论与方法[M]. 2版. 北京: 清华大学出版社, 2006: 146-147. [本文引用:2]
[11]	刘晓佳, 兰培真, 郑高哲. 可持续发展的综合交通运输系统构成模型研究[J]. 武汉理工大学学报: 交通科学与工程版, 2011, 35(1): 122-125. Liu Xiao-jia, Lan Pei-zhen, Zheng Gao-zhe. Research on sustainable comprehensive transportation system composition model[J]. Journal of Wuhan University of Technology (Transportation Science and Engineering Edition), 2011, 35(1): 122-125. [本文引用:1]
[12]	史峰, 王辉, 郁磊, 等. 智能算法[M]. 北京: 北京航空航天大学出版社, 2011: 69-70. [本文引用:1]

1983

0.0

... 0 引言现有运输通道布局优化研究中,常见的是以城市交通为对象进行网络优化设计,或是将各种运输方式和客货运单独分析^[1,2,3,4] ...

2005

0.0

. 2005, 3(2):57-62 DOI:doi:10.3969/j.issn.1672-4747.2005.02.010

Trip assignment model for transportation corridor based on network equilibrium

基于网络的运输通道客运流量分配模型

Li You-hao , Liu Xiao-jia , Shi Qi-zhou.

李友好, 刘晓佳, 施其洲

根据各运输方式的经济技术特征,构建了运输通道的时空运营网络来表示各运输方式的竞争性。认为旅客的时间价值(VOT)分布的概率密度函数服从对数正态分布,旅客的广义出行费用取票价和时间两个参数,运用城市交通分配网络均衡思想,提出基于网络的区域运输通道多交通模式客流分配模型,建立了用户最优和系统最优两个目标函数,并给出了模型的求解方法。用一数值示例验证了模型的有效,分析了模型对政府和运输经营企业决策的指导意义。

... 0 引言现有运输通道布局优化研究中,常见的是以城市交通为对象进行网络优化设计,或是将各种运输方式和客货运单独分析^[1,2,3,4] ...

2007

0.0

... 0 引言现有运输通道布局优化研究中,常见的是以城市交通为对象进行网络优化设计,或是将各种运输方式和客货运单独分析^[1,2,3,4] ...

1986

0.0

... 0 引言现有运输通道布局优化研究中,常见的是以城市交通为对象进行网络优化设计,或是将各种运输方式和客货运单独分析^[1,2,3,4] ...

2010

0.0

. 2010, 50(6):815-819

Tri-level programming model for optimization of regional transportation corridor layout

区域运输通道布局优化三层规划模型

Liu Qiang , Lu Hua-pu , Wang Qing-yun.

刘强, 陆化普, 王庆云

... 刘强等^[5]和李艳红等^[6]分别用三层规划模型和多目标决策优化方法对区域综合运输通道进行了研究,前者未说明模型中的运价与现实中运价制订的关系,后者并未考虑交通流改变下的网络优化问题 ...

... 综合交通网络随机配流模型^[5]描述通道内用户的交通选择过程见式(7) ...

2009

0.0

. 2009, 39(6):1481-1485

Combined capacity optimization of comprehensive transportation corridor based on multi-objective decision making

基于多目标决策的综合运输通道组合运能优化

Li Yan-hong , Yuan Zhen-zhou , Chen Jing-yun

李艳红, 袁振洲, 陈静云

2010

0.0

... 城市范围内的路网小区划分,是按照一定参照指标分成若干个交通小区,每个小区作为交通量发生和吸引的出发地和目的地,在这种交通分配模型中,所有交通量均认为从一个交通小区的质心点到另一个交通小区的质心点^[7] ...

2001

0.0

... 交通需求会随着运输网络的变化而变化,研究此类问题时宜使用弹性需求的用户平衡(User equilibrium,UE)模型和随机用户平衡(Stochastic user equilibrium,SUE)模型^[8,9] ...

2004

0.0

2006

0.0

... 对于公路网中通道,依据美国道路局开发的BPR函数^[10],运输时间与交通交通量的数学形式为: ...

... 15,β=4,均为美国道路局前期的推荐赋值^[10] ...

2011

0.0

. 2011, 35(1):122-125 DOI:doi:10.3963/j.issn.1006-2823.2011.01.029

Research on sustainable comprehensive transportation system composition model

可持续发展的综合交通运输系统构成模型研究

Liu Xiao-jia , Lan Pei-zhen , Zheng Gao-zhe.

刘晓佳, 兰培真, 郑高哲

在确立各种运输方式可持续发展评价指标体系的基础上,设计出信息熵法与灰色关联度评价法相结合的组合评价模型,运用该模型对各种运输方式的可持续发展能力进行评价,并据此建立可持续发展的综合交通系统构成模型,为创建可持续发展的综合交通运输提供定量化的指导方案,实现交通与环境、能源、社会、经济的和谐发展.

... 可持续发展成本系数 λ:在交通量一定时,不同运输方式下的交通量比例构成总成本最小,通过多目标决策灰色关联度评价法^[11]来确定 ...

2011

0.0

... 其次,对于城市群综合运输通道布局优化模型中变量较多,可行解空间大,使用传统遗传算法时可能存在未成熟收敛的现象^[12],本文使用多种群遗传算法 ...