舰载直升机复杂舰面上的动力学分析

引用本文

王倩, 赵丁选, 赵颖, 陈娜. 舰载直升机复杂舰面上的动力学分析. 2017, 47(4): 1109-1113
WANG Qian, ZHAO Ding-xuan, ZHAO Ying, CHEN Na. Dynamic analysis of carrier helicopter on complex deck. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1109-1113 复制到剪切板

Permissions

舰载直升机复杂舰面上的动力学分析

王倩, 赵丁选, 赵颖, 陈娜

吉林大学机械科学与工程学院,长春 130022

通讯作者：赵丁选(1965-),男,教授,博士生导师.研究方向:工程机械,机械动力学,可靠性工程.E-mail:zdx@jlu.edu.cn

作者简介:王倩(1989-),女,博士研究生.研究方向:工程机械动力学.E-mail:wangqianqianer@126.com

基金:高等学校博士生学科点专项科研基金项目(2012061110023); 吉林大学“985工程”项目.

摘要

对舰载直升机着舰后的运动动力学进行了研究。首先针对海浪信号的随机不确定性,根据海浪波理论,提出了海浪信号的数学模型,然后利用海浪谱描述海浪的统计特性,运用MATLAB仿真平台仿真出不规则海浪并对其进行谱分析。最后基于拉格朗日方程,建立了着舰的机身动力学模型,对摇摆舰艇上的舰载机进行了动力学仿真并采用龙格库塔法对动力学模型进行实时解算。

关键词: 工程机械; 舰载直升机; 海浪模型; 动力学模型; 实时仿真

中图分类号:TP18;TH17 文献标志码:A 文章编号:1671-5497(2017)04-1109-05

Dynamic analysis of carrier helicopter on complex deck

WANG Qian, ZHAO Ding-xuan, ZHAO Ying, CHEN Na

College of Mechanical Science and Engineering, Jilin University,Changchun 130022, China

Abstract

The landing dynamics of the carrier helicopter on complex deck was studied. First, the random uncertainty of sea wave signal was considered, and the mathematical model of the sea wave signals was proposed according to the wave theory. The statistic characteristics of the sea wave were described by the way of sea wave spectrum. The irregular approximate progressing waves were simulated on MATLAB simulation platform, and the spectral estimation of the sea waves was conducted. Then, the landing dynamic model of the fuselage was established based on Lagrange equation. Finally, the dynamics simulation of the carrier helicopter on the complex deck was carried out and the Runge-Kutta method was used for the real-time calculation of the dynamic model.

Keyword: construction machinery; carrier helicopter; sea waves; dynamics model; real-time calculation

Show Figures

0 引言

由于舰载直升机具有许多其他飞行器难以达到或者不可能达到的优势从而被广泛地应用于军事和非军事行动中。它能以多批次的战斗群起降于中、小型舰艇上执行作战任务^{[1, 2]}。可是海况复杂, 瞬息万变, 若遇上风浪, 船体大幅度横摇升沉, 给舰载机着舰带来了一定危险。为了能进一步了解舰艇摆动对舰载机的影响, 本文对舰载机着舰后的运动动力学^{[3, 4]}进行了研究。将舰载机在甲板上的运动视为在舰体连体坐标系中的相对运动, 根据动力学原理^[2]推导出舰载机在舰体连体坐标系中的动力学方程, 并结合推导出的舰艇在波浪中的摇摆方程, 对在摇摆舰艇上的舰载机进行了动力学仿真。本文方法可以对舰载机着舰的结果进行预判, 大大降低了舰载机着舰的危险系数。

1 波浪模型

1.1 规则波模型

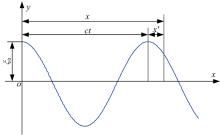
根据流体力学知识可假设流体不可压缩, 波浪以速度 $\begin{matrix} c 沿 x \end{matrix}$ 轴正方向前进。在波浪坐标系内余弦曲线如图1所示。

	Figure Option View Download New Window
	图1 规则波浪示意图Fig.1 Schematic diagram of regular waves

根据图1波浪的余弦曲线方程为

$\begin{matrix} Y = ξ_{a} \cos (2 π \cdot \frac{x'}{λ}) (1) \end{matrix}$

式中: $\begin{matrix} Y \end{matrix}$ 为波面与静水面的高度; $\begin{matrix} ξ_{a} \end{matrix}$ 为波浪振幅; $\begin{matrix} λ \end{matrix}$ 为波长, 其中

$\begin{matrix} x' = x - ct (2) \end{matrix}$

式中: t为时间; x为考察点在波浪传播方向与原点的距离。

1.2 不规则波模型

实际应用中的不规则浪常用统计特性来描述, 其中对数据做谱分析, 进行无因次与数学拟合得到波浪在不同频率的能量分布— — 浪谱^[5]。根据流体力学理论可知, 单位面积内的单个谐波能量为:

$\begin{matrix} U = \frac{1}{2} ρg {(ξ_{ai})}^{2} (3) \end{matrix}$

根据叠加理论, 在频率从 $\begin{matrix} ω_{i} \end{matrix}$ 变化到 $\begin{matrix} ω_{i} + Δω \end{matrix}$ 的波的能量为:

$\begin{matrix} U = \frac{1}{2} ρg \underset{Δω}{Σ} {(ξ_{ai})}^{2} (4) \end{matrix}$

定义函数 $\begin{matrix} S (ω) \end{matrix}$ 使得U= $\begin{matrix} \frac{1}{2} \end{matrix}$ ρ g $\begin{matrix} \sum_{Δω} \end{matrix} \begin{matrix} {(ξ_{ai})}^{2} \end{matrix}$ =ρ gS(ω )Δ ω 成立。若使 $\begin{matrix} Δω \end{matrix}$ 趋近于0且谐波数目无穷多时, 随机波浪在单位面积内的能量可以表示为:

$\begin{matrix} U = \frac{1}{2} ρg \overset{\infty}{\sum_{i \to 1}} {(ξ_{ai})}^{2} = ρg \int_{0}^{\infty} S (ω) dω (5) \end{matrix}$

式中: $\begin{matrix} S (ω) \end{matrix}$ 称为浪谱, 根据上式可由浪谱求得谐波的振幅为:

$\begin{matrix} ξ_{ai} = \sqrt[]{2 S (ω) Δω} (6) \end{matrix}$

皮尔逊-莫斯柯维奇谱简称P-M谱, 由学者Pierson和Moscowitz对大西洋风浪的观察资料整理分类并进行谱分析后得到, P-M谱仅由风速决定, 能很好地替代实际的随机海浪谱, 广泛应用于工程中^[6]。其表达式为:

$\begin{matrix} \begin{matrix} S (ω) = \frac{8.1 \times 10^{- 3} g^{2}}{ω^{5}} \exp [- 0.74 {(\frac{g}{vω})}^{4}] \\ (7) \end{matrix} \end{matrix}$

式中: $\begin{matrix} v \end{matrix}$ 为海面上19.5 m高处的平均风速; $\begin{matrix} ω \end{matrix}$ 为波浪角速度; $\begin{matrix} g \end{matrix}$ 为重力加速度。

2 舰艇在不规则海浪下的摇摆分析

由于海况复杂多变, 基本把海浪视为不规则浪, 而不规则海浪可以视为规则海浪的叠加, 因此舰艇在不规则海浪作用下的摆动可以看做是舰艇在不同规则海浪作用下摆动的叠加^{[6, 7, 8]}。

若舰艇以 $\begin{matrix} v_{0} \end{matrix}$ 速度前进, 前进方向与主波方向的夹角为 $\begin{matrix} δ, \end{matrix}$ 则舰艇摆动位移方程式表示如下:

$\begin{matrix} \begin{matrix} η_{i} (t) = \sum_{m} \sum_{n} RAO \times ζ_{mn} \times \cos {ε_{mn} - (ω_{ε})_{mn} \\ + σ_{i} [{(ω_{ε})}_{mn}]} (8) \end{matrix} \end{matrix}$

式中: $\begin{matrix} ζ_{mn} \end{matrix}$ 为浪高, 由 $\begin{matrix} ζ_{mn} = \sqrt[]{2 S (ω_{e}, χ) Δω} \end{matrix}$ 求出; m与n分别为按波浪分量的频率和波浪分量的方向叠加; $\begin{matrix} ε_{mn} \end{matrix}$ 为当前波浪分量相位的随机初值; $\begin{matrix} ω_{e} \end{matrix}$ 为遭遇频率, 由 $\begin{matrix} ω_{e} = |ω - \frac{ω^{2} υ_{0}}{g} cosδ| \end{matrix}$ 求出; RAO为振幅响应算子, 是遭遇频率、船速以及舰艇结构参数的函数, 通常由切片理论 $\begin{matrix} RAO = |\bar{η_{i}} [(ω_{e})_{mn}, δ, v_{0}]| \end{matrix}$ 求出; $\begin{matrix} δ_{i} [{(ω_{e})}_{mn}] \end{matrix}$ 为相位响应算子, 由 $\begin{matrix} δ_{i} [{(ω_{e})}_{mn}] = ta n^{- 1} (\frac{RA O_{虚部}}{RA O_{实部}}) \end{matrix}$ 求出。

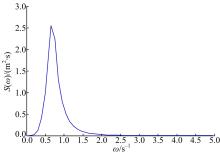
假设风速为14 m/s, 舰艇在4级海况下根据式(8)可得出海浪谱函和海浪摆动的图像如图2所示。

	Figure Option View Download New Window
	图2 4级海况下的浪谱函数图Fig.2 Spectrum map of state 4 wave

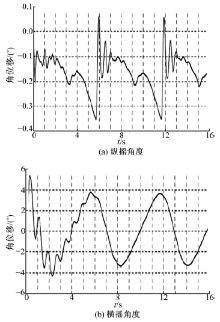
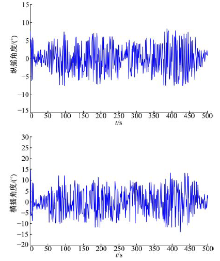根据图2可知浪谱函数主要区域为 $\begin{matrix} ω = 0.4 ~ 1.0 \end{matrix}$ 的区域中, 假设舰艇速度为零, 舰艇朝向与波浪方向夹角为135° , 可由式(8)求出舰艇各运动自由度的响应。计算出各自由度的振幅响应算子和相位响应算子带入式(8), 即可求出舰艇运动幅度与时间的关系, 如图3和图4所示。

	Figure Option View Download New Window
	图3 4级海况时的舰艇的纵摇和横摇角度随时间变化曲线Fig.3 Variation curves of time versus angle when ship pitching and rolling

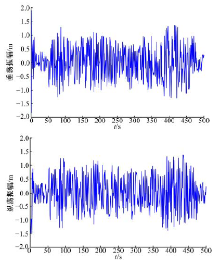	Figure Option View Download New Window
	图4 4级海况时的舰艇的垂荡和纵荡振幅随时间变化曲线Fig.4 Variation curves of time versus amplitude when ship heaving and pitching

由图4可以看出:在第205~240 s、420~440区间为运动平稳期, 下文的仿真实验最初给定了航向与航速的运动数据, 并用该方法计算了480 s内的舰载运动记录成数据文件, 为下文仿真时实时调用。

3 舰载机几何关系分析

设初始时刻固定坐标系位置与舰载机连体坐标系位置重合, 瞬时舰载机相对固定坐标系的方位以横倾角 $\begin{matrix} λ 、 \end{matrix}$ 偏航角 $\begin{matrix} φ 、 \end{matrix}$ 纵倾角 $\begin{matrix} θ \end{matrix}$ (单位均为弧度)表示, 从该瞬时舰载机连体坐标向下一瞬时舰载机连体坐标转换用N表示, α 、β 、γ 分别为横倾角、偏航角、纵倾角, 而舰艇坐标系到舰载机坐标系转换用N_s表示:

$N = [\begin{matrix} 1 & - γ & β \\ γ & 1 & - α \\ - β & α & 1 \end{matrix}] (9)$

$\begin{matrix} \begin{matrix} N_{s} = [\begin{matrix} n_{11} & n_{12} & sinλsinφ & x \\ n_{21} & n_{22} & - cosλsinφ & y \\ sinφsinθ & sinφcosθ & cosφ & z \\ 0 & 0 & 0 & 1 \end{matrix}] (10) \end{matrix} \end{matrix}$

式中:n₁₁=cosλ cosθ -sinλ cosφ sinθ ; n₁₂=-cosλ sinθ -sinλ cosφ cosθ ; n₁₃=sinλ sinφ ; n₂₁=sinλ cosθ +cosλ cosφ sinθ ; n₂₂=-sinλ sinθ +cosλ cosφ cosθ ; n₂₃=-cosλ sinφ 。

舰载机质心在固定坐标系中新坐标分量可根据转换矩阵与连体坐标系中直升机质心坐标求得, 公式如下:

$\begin{matrix} [\begin{matrix} x_{MC} \\ y_{MC} \\ z_{MC} \end{matrix}] = [\begin{matrix} {(\vec{{r^{H}}_{MC}})}_{x} + {(\vec{{r^{H}}_{MC}})}_{z} β - {(\vec{{r^{H}}_{MC}})}_{y} γ \\ {(\vec{{r^{H}}_{MC}})}_{y} + {(\vec{{r^{H}}_{MC}})}_{x} γ - {(\vec{{r^{H}}_{MC}})}_{z} α \\ {(\vec{{r^{H}}_{MC}})}_{z} + {(\vec{{r^{H}}_{MC}})}_{y} α - {(\vec{{r^{H}}_{MC}})}_{x} β \end{matrix}] (11) \end{matrix}$

4 建立动力学方程

根据拉格朗日方程, 建立动力学方程如下:

$\begin{matrix} \begin{matrix} \frac{d}{dt} (\frac{\partial T}{\partial {\overset{\cdot \cdot}{q}}_{j}}) - \frac{\partial T}{\partial q_{j}} + \frac{\partial V}{\partial q_{j}} - \frac{\partial F}{\partial {\overset{\cdot}{q}}_{j}} = Q_{j} (12) \\ i = 1, 2, \dots, n \end{matrix} \end{matrix}$

式中:T为动能; V为势能; F为耗散能; Q为广义力。

4.1 系统动能表达式

根据6自由度刚体动能的计算方式^[9]和模型中提出的假设, 舰载机平面被视为是对称的, 故转动惯量与惯性积 $\begin{matrix} J_{HX} 、 J_{HY} 、 J_{HXY} 、 J_{HYZ} \end{matrix}$ 为零(直升机主要技术参数见文献^[10]), 则此时的动能表达式如下:

$\begin{matrix} \begin{matrix} T = \frac{1}{2} m_{H} ({\overset{\cdot}{x}}_{MC}^{2} + {\overset{\cdot}{y}}_{MC}^{2} + {\overset{\cdot}{z}}_{MC}^{2}) + \frac{1}{2} J_{HX} {\overset{\cdot}{α}}^{2} + \\ \frac{1}{2} J_{HY} {\overset{\cdot}{β}}^{2} + \frac{1}{2} J_{HZ} {\overset{\cdot}{γ}}^{2} - J_{HXY} \overset{\cdot}{α} \overset{\cdot}{β} - J_{HYZ} \overset{\cdot}{β} \overset{\cdot}{γ} \\ - J_{HXZ} \overset{\cdot}{α} \overset{\cdot}{γ} (13) \end{matrix} \end{matrix}$

式中: $\begin{matrix} m_{H} \end{matrix}$ 为舰载机质量; $\begin{matrix} J_{HX} 、 J_{HY} 、 J_{HZ} \end{matrix}$ 为转动惯量; J_HXY 、J_HXZ 、J_HYZ为惯性积。

4.2 系统重力势能表达式

设世界坐标系先绕舰艇连体坐标系Z_s轴旋转h, 再绕新生成舰艇连体坐标系X_s轴旋转ρ , 最后绕新生成的连体坐标系Y_s轴旋转κ , 经过三次旋转后生成新舰艇连体坐标系。根据式(10)可得从舰艇坐标系到舰载机连体坐标系的转换矩阵N_s, 设G_HX 、G_HY 、G_HZ是重力方向向量在直升机连体坐标系中的3个分量, 其表达式如下:

$\begin{matrix} [\begin{matrix} G_{HX} \\ G_{HY} \\ G_{HZ} \end{matrix}] = {(N_{s})}^{- 1} \times [\begin{matrix} cosρsinκ \\ sinρ \\ cosρcosκ \end{matrix}] (14) \end{matrix}$

则直升机重力势能表达式如下:

$\begin{matrix} U = mgsinλs inφ G_{HX} - mgcosλsinφ G_{HY} + cosφ G_{HZ} (15) \end{matrix}$

4.3 广义力的计算

根据广义坐标的选取, 舰载机在飞机或着舰过程中, 有旋翼升力 $\begin{matrix} T_{S} \end{matrix}$ 可参见文献^[10], 尾浆侧向力 $\begin{matrix} T_{TR} \end{matrix}$ 可参见文献^[11], 空气阻力 $\begin{matrix} Q_{F} 、 \end{matrix}$ 旋翼的反扭矩 $\begin{matrix} M_{K}, \end{matrix}$ 可参见文献^[12], 空气阻力 $\begin{matrix} M_{x} \end{matrix}$ 和阻力矩 $\begin{matrix} M_{z} \end{matrix}$ 对直升机机身做功, 将以上力和力矩代入式(12)中得广义力矩阵表达式为:

$\begin{matrix} {[Q_{i}]}_{6 \times 1} = {[Q_{x}, Q_{y}, Q_{z}, Q_{α}, Q_{β}, Q_{λ}]}^{T} (16) \end{matrix}$

4.4 动力学方程

将式(13)~(16)代入式(12), 得到集飞行与着陆于一身的直升机动力学方程, 其表达式如下:

$\begin{matrix} {[A]}_{6 \times 6} [\overset{\cdot \cdot}{q}] + {[B]}_{6 \times 6} [\overset{\cdot}{q}] + {[C]}_{6 \times 6} [q] = {[Q]}_{6 \times 1} (17) \end{matrix}$

式中: $\begin{matrix} {[q]}_{6 \times 6} \end{matrix}$ 为广义坐标矩阵, 即 $\begin{matrix} {[q]}_{6 \times 6} = {[x, y, z, α, β, γ]}^{T}; {[Q]}_{6 \times 6} \end{matrix}$ 为广义力矩阵。

5 动力学模型的解算及其结果

对于高阶微分方程组本文选用在工程上应用广泛的高精度单步算法— — 四阶龙格库塔方法。本文首先用中间变量 $\begin{matrix} [\overset{\cdot}{q}] \end{matrix}$ 将二阶微分方程组降阶为一阶微分方程组, 并赋予 $\begin{matrix} [\overset{\cdot}{q}] \end{matrix}$ 和 $\begin{matrix} [q] \end{matrix}$ 初始值, 然后根据精度四阶龙格库塔公式进行求解。给定直升机处于舰艇连体坐标中的位置和舰艇摇摆的相关数值, 为了尽量缩小视景程序对动力学解算的拖慢效应, 故将龙格库塔算法的步长增大到0.02 s。按以上设定对直升机动力学方程进行求解, 结果如图5和图6所示。

	Figure Option View Download New Window
	图5 舰载机质心位移随时间变化曲线Fig.5 Variation curve of time versus displacement of helicopter centroid

	Figure Option View Download New Window
	图6 舰载机摇动角度随时间变化曲线Fig.6 Time variation curve of helicopter swing

由图5(a)可以看出, 舰载机在横向方向的振动是自身固有频率振动与受海浪冲击的受迫振动的合成。由图5(b)可以看出, 随着船舰的摇动, 当纵摇摆角度变大时, 直升机开始沿舰面滑动。

图6反映出舰艇在海浪作用下的摆动情况, 舰载机纵摇与纵向位移的趋势相同。舰载机的横摇的固有振动衰减后, 直升机随海浪频率横摇。

6 结束语

本文分析了舰载机与舰艇系统的模型, 并推导出其动力学方程。运用该模型能够预测出舰艇的摇摆对舰面上直升机的影响。根据本文仿真结果得出, 当海浪运动幅值较大时, 舰载机在舰面上处于危险状态。运用该方法能够比较准确地反映出舰载机在摇摆舰艇面上的运动状态, 为预测直升机在摇摆舰艇平面上的运动提供了一种新方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	赵丁选, 王倩, 张祝新. 基于层次分析法的可拓学理论对舰载直升机可靠性的评估[J]. 吉林大学学报: 工学版, 2016, 46(5): 1528-1531. Zhao Ding-xuan, Wang Qian, Zhang Zhu-xin . Extenics theory for reliability assessment of carrier helicopter based on analytic hierarchy process[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(5): 1528-1531. [本文引用:1]
[2]	Yavrucuk L, Kubali E, Tarimci O, et al. A low cost flight simulatou using virtual reality tools[J]. IEEE Aerospace and Electronic Systems Magazine, 2011, 26(4): 10-14. [本文引用:2]
[3]	栗英杰, 赵丁选, 李保中, 等. 基于IDRA法的直升机动力学建模[J]. 华中科技大学学报: 自然科学版, 2014, 42(1): 98-102. Li Ying-jie, Zhao Ding-xuan, Li Bao-zhong, et al. Dynamics modeling for helicopter based on IDRA approach[J]. Journal of Huazhong University of Science & Technology(Natural Science Edition), 2014, 42(1): 98-102. [本文引用:1]
[4]	Konstant K, Carsten D. Mechanical model and control of an autonmous small sized helicopter with a stiff main rotor[C]//Proceedings of 2004 IEEE/RSJ International Conefemce on Intelliegnt Robots Systems, Tokyo, 2004: 2469-2474. [本文引用:1]
[5]	陈虹丽, 李爱军, 贾红宇. 海浪信号的实时仿真和谱估计[J]. 电机与控制学报, 2007, 11(1): 93-96. Chen Hong-li, Li Ai-jun, Jia Hong-yu. Real time simulation and spectral analysis of sea wave signal[J]. Electric Machines and Control, 2007, 11(1): 93-96. [本文引用:1]
[6]	Fang M C, Luo J H, Lee M L. A nonlinear mathematical model for ship turning circle simulation in wave[J]. Journal of Ship Research, 2005, 49(2): 69-79. [本文引用:2]
[7]	Claes Johanson. Real-time water rendering introducing the projected grid concept[D]. Sweden: Department of Computer Science, Lund University, 2004. [本文引用:1]
[8]	Tristan Perez, Mogens Blanke. Simulation of ship motion in seaway[R]. Orsted DTU, Denmark: Technical University of Denmark, 2002: 1-15. [本文引用:1]
[9]	Cai G W, Chen B M, Lee T H. An overview on development of miniature unmanned rotorcraft systems[J]. Front Electr Eng China, 2010, 5(1): 1-14. [本文引用:1]
[10]	普劳蒂R W. 直升机性能及稳定性和操纵性[M]. 高正, 译, 北京: 航空工业出版社, 1990. [本文引用:2]
[11]	Dzul A, Lozano R, Castillo P. Adaptive control for a radio-controlled helicopter in a vertical flying stand [J]. International Journal of Adaptive Control and Signal Processing, 2004, 18(5): 473-485. [本文引用:1]
[12]	Hoffmann G M, Huang H M, Wasland er S L, et al. Tomlin precision flight control for a multi-vehicle quadrotor helicopter testbed[J]. Control Engineering Practice, 2011, 19(9): 1023-1036. [本文引用:1]

2016

0.0

. 2016, 46(5):1528-1531

Extenics theory for reliability assessment of carrier helicopter based on analytic hierarchy process

基于层次分析法的可拓学理论对舰载直升机可靠性的评估

Zhao Ding-xuan , Wang Qian , Zhang Zhu-xin .

赵丁选, 王倩, 张祝新

... 它能以多批次的战斗群起降于中、小型舰艇上执行作战任务^[1,2] ...

2011

0.0

... 它能以多批次的战斗群起降于中、小型舰艇上执行作战任务^[1,2] ...

... 将舰载机在甲板上的运动视为在舰体连体坐标系中的相对运动,根据动力学原理^[2]推导出舰载机在舰体连体坐标系中的动力学方程,并结合推导出的舰艇在波浪中的摇摆方程,对在摇摆舰艇上的舰载机进行了动力学仿真 ...

2014

0.0

. 2014, 42(1):98-102 DOI:doi:10.13245/j.hust.140121

Dynamics modeling for helicopter based on IDRA approach

基于IDRA法的直升机动力学建模

Li Ying-jie , Zhao Ding-xuan , Li Bao-zhong

栗英杰, 赵丁选, 李保中

摘　要：为加快直升机动力学模型的解算速度，基于拉格朗日方程，以一个仿真步长内机身的微小位移和转角（IDRA）为广义坐标，提出了直升机动力学建模的IDRA法，简化了相邻步长间机体坐标系的转化矩阵，节省了CPU计算时间。同时，将直升机轮胎视为带有黏性阻尼的三维线性弹簧，将其势能、动能和耗散能用新的广义坐标表示，建立了集飞行与着陆于一身的机身动力学模型。实验结果表明：与传统方法相比，利用IDRA 法可以节省1/3的CPU计算时间，飞行与着陆之间曲线过渡合理，从而验证了该方法的可靠性和实时性。

... 为了能进一步了解舰艇摆动对舰载机的影响,本文对舰载机着舰后的运动动力学^[3,4]进行了研究 ...

2004

0.0

... 为了能进一步了解舰艇摆动对舰载机的影响,本文对舰载机着舰后的运动动力学^[3,4]进行了研究 ...

2007

0.0

. 2007, 11(1):93-96 DOI:doi:10.3969/j.issn.1007-449X.2007.01.021

Real time simulation and spectral analysis of sea wave signal

海浪信号的实时仿真和谱估计

Chen Hong-li, Li Ai-jun, Jia Hong-yu

陈虹丽, 李爱军, 贾红宇

针对海浪信号的随机不确定性问题,依据长峰波海浪理论,给出了海浪信号的数学模型,提出了一种海浪信号的实时仿真方法.采用波能谱(海浪谱)描述海浪的统计特性,采用海浪反演的线性叠加法在Matlab仿真平台上实时仿真出不规则长峰波海浪;利用加矩形窗口的Welch谱估计法对仿真出的海浪做了谱估计,同时与真实谱进行比较.结果表明,该海浪信号的仿真方法既能满足实时仿真的要求,又具有较高的仿真精确度.船舶减摇控制的应用证明,该方法能为船舶运动控制仿真系统提供可靠的海浪扰动信号.

... 浪谱^[5] ...

2005

0.0

... 皮尔逊-莫斯柯维奇谱简称P-M谱,由学者Pierson和Moscowitz对大西洋风浪的观察资料整理分类并进行谱分析后得到,P-M谱仅由风速决定,能很好地替代实际的随机海浪谱,广泛应用于工程中^[6] ...

... 2 舰艇在不规则海浪下的摇摆分析由于海况复杂多变,基本把海浪视为不规则浪,而不规则海浪可以视为规则海浪的叠加,因此舰艇在不规则海浪作用下的摆动可以看做是舰艇在不同规则海浪作用下摆动的叠加^[6,7,8] ...

2004

0.0

2002

0.0

2010

0.0

... 1 系统动能表达式根据6自由度刚体动能的计算方式^[9]和模型中提出的假设,舰载机平面被视为是对称的,故转动惯量与惯性积 JHX、JHY、JHXY、JHYZ为零(直升机主要技术参数见文献^[10]),则此时的动能表达式如下: ...

1990

0.0

... 3 广义力的计算根据广义坐标的选取,舰载机在飞机或着舰过程中,有旋翼升力 TS可参见文献^[10],尾浆侧向力 TTR可参见文献^[11],空气阻力 QF、旋翼的反扭矩 MK,可参见文献^[12],空气阻力 Mx和阻力矩 Mz对直升机机身做功,将以上力和力矩代入式(12)中得广义力矩阵表达式为: ...

2004

0.0

2011

0.0