联合载荷下角接触球轴承静态接触特性分析

引用本文

徐涛, 赵玉洁, 邵晴, 张友鹤, 徐天爽, 于征磊. 联合载荷下角接触球轴承静态接触特性分析. 2017, 47(4): 1114-1120
XU Tao, ZHAO Yu-jie, SHAO Qing, ZHANG You-he, XU Tian-shuang, YU Zheng-lei. Analysis of static contact characteristics of angular contact ball bearing under combined loads. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1114-1120 复制到剪切板

Permissions

联合载荷下角接触球轴承静态接触特性分析

徐涛, 赵玉洁, 邵晴, 张友鹤, 徐天爽, 于征磊

吉林大学机械科学与工程学院,长春 130022

通讯作者：徐天爽(1985-),女,讲师,博士.研究方向:计算力学.E-mail:xts@jlu.edu.cn

作者简介:徐涛(1955-),女,教授,博士生导师.研究方向:计算力学.E-mail:xutao@jlu.edu.cn

基金:国家自然科学基金项目(51505181); 教育部博士学科点专项科研基金项目(20130061120035).

摘要

针对角接触球轴承结构进行静态接触特性分析,研究了联合载荷对结构接触特性的影响机制。依据赫兹接触理论,设定了求解接触应力与接触角的计算方法;利用ANSYS软件建立了角接触球轴承结构模型,并提出了加载方案及约束的设定方法;将仿真结果与赫兹理论结果进行对比,验证了本文建模方法、加载方式的正确性。最后,利用本文模型探讨了联合载荷下的接触应力、接触应变、接触角、接触椭圆的变化规律及影响,为复杂加载工况下轴承的设计及应用提供工程分析参考。

关键词: 机械设计; 角接触球轴承; 联合载荷; 接触应力; 接触角; 接触椭圆

中图分类号:TH133.3 文献标志码:A 文章编号:1671-5497(2017)04-1114-07

Analysis of static contact characteristics of angular contact ball bearing under combined loads

XU Tao, ZHAO Yu-jie, SHAO Qing, ZHANG You-he, XU Tian-shuang, YU Zheng-lei

College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China

Abstract

The static contact characteristic of the angular contact ball bearing is analyzed and the influence mechanism of load is studied when the bearing is under combined loads. The solution of the loads and contact angles is put forward in combination with Hertz contact theory. The finite element model is established in ANSYS. The distribution and transformation law of the contact parameters under combined loads are explored. The simulation results are consistent with theoretical values. It is revealed that the model and boundary conditions are correct and rational. The changes of contact stress, contact strain, contact angle and contact ellipse are investigated. This study may provide engineering analysis reference for the design and application of rolling bearing under complex loading conditions.

Keyword: mechanical design; angular contact ball bearing; combined load; contact load; contact angle; contact ellipse

Show Figures

0 引言

角接触球轴承以其能同时承受径向与轴向载荷、生产精度高等优点, 在机械传动中起着重要作用。研究轴承内部的载荷分布模式、大小及产生的应力应变影响是轴承接触分析的重要环节。

近年来, 国内外诸多学者对接触问题做了研究。Tatjana^[1]和He等^[2]通过理论计算得到外部载荷对轴承内部载荷分布的影响。方兵等^[3]采用坐标变换方法建立角接触球轴承滚动体接触变形的几何关系。Liao^[4]研究了施加单一载荷时接触应力与接触半径随着载荷变化而变化的规律。Radoslav^[5]分析了在轴承内圈上施加径向载荷对轴承应力分布的影响, 提出了相应的数学模型。Tang等^[6]基于赫兹接触理论, 建立了轴承有限元模型并对其施加径向载荷, 仿真结果与赫兹理论的计算结果基本一致。Zhao等^[7]和Ricci^[8]研究了轴承在单一轴向载荷作用下, 其接触角与内外圈的接触应力随轴向载荷的变化规律。颜诚等^[9]以受轴向载荷时轴承承载能力的算法为基础, 提出了基于联合载荷的角接触球轴承接触分析的改进算法, 仿真结果表明:轴承轴向变形与轴向载荷之间、径向变形与径向载荷之间均是线性递增关系。刘显军等^[10]的研究表明, 同一轴向载荷下, 增大径向载荷会使接触角减小, 导致轴向变形有所减小; 同一径向载荷下, 增大轴向载荷会使接触角增大, 导致径向变形增大; 但其结果为实验结果, 且未涉及对于接触椭圆长、短半轴的大小随联合载荷大小的变化规律影响。

工程实际中轴承往往会同时承受来自径向和轴向的联合载荷作用, 本文深入探讨了联合载荷对轴承结构接触特性的影响机制及接触参数的变化规律, 研究了联合载荷的变化对其接触应力、接触角、接触椭圆的影响。

1 模型建立与边界条件设定

1.1 有限元模型建立

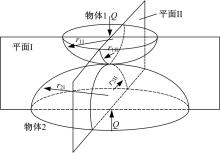
图1为7014角接触球轴承, 材料为轴承钢, 基本参数见表1。为简化计算, 模型中忽略其保持架的影响, 只考虑钢球与内外圈的相互作用。不妨取整体模型中最大承载钢球的1/2对称模型作为研究对象进行静力学分析, 如图2所示。以1/2钢球切面为工作平面, 钢球中心为坐标系原点, 利用ANSYS软件建立结构三维实体模型。单元类型选用SOLID186, 弹性模量为2.06× 10⁵ MPa, 泊松比为0.3, 摩擦因数为0.03。

	Figure Option View Download New Window
	图1 7014球轴承实物图Fig.1 7014 ball bearing

表1 轴承基本参数 Table 1 Main parameters of bearing

名称	符号	数值	名称	符号	数值
外径	R/mm	110	接触角	$\begin{matrix} α \end{matrix}$ /(° )	18
内径	$\begin{matrix} r \end{matrix}$ /mm	70	球径	$\begin{matrix} D_{w} \end{matrix}$ /mm	12
球数	$\begin{matrix} z \end{matrix}$	21	外圈沟道比	$\begin{matrix} f_{R} \end{matrix}$	0.53
宽度	L/mm	20	内圈沟道比	$\begin{matrix} f_{r} \end{matrix}$	0.52

表1 轴承基本参数 Table 1 Main parameters of bearing

	Figure Option View Download New Window
	图2 有限元模型示意图Fig.2 Sketch map of finite element model

为方便网格划分, 对整个模型扫略划分, 在钢球与内外圈沟道可能发生接触的位置细化网格以提高计算精度。接触设置采用面面接触, 选取内圈外表面与外圈内表面作为目标面, 将钢球表面设置为柔性接触面, 内、外套圈的法向接触刚度分别设为1和1.2, 穿透容差因子均为0.1。

1.2 边界条件设定

约束:①对模型的剖面施加对称约束; ②由于外圈外表面安装在轴承座上, 故施加全约束; ③在笛卡尔坐标系下耦合内圈装配面的x、y方向施加位移约束, 以此来模拟内圈在联合载荷下的倾斜; ④对滚动体中心施加切向位移约束。

加载:在内圈端面施加轴向载荷, 在内圈下半面以余弦载荷的方式施加径向载荷。

经分析计算可知, 余弦载荷的方式更加符合实际工况, 加载范围为整个轴承的下半圈, 如图3所示。余弦函数计算公式为: $\begin{matrix} P = 8 F_{r} cosθ / (3 \sqrt[]{3} rL), 其中 P \end{matrix}$ 为余弦力, $\begin{matrix} F_{r} \end{matrix}$ 为施加的径向载荷, $\begin{matrix} θ \end{matrix}$ 为图3所示施加载荷的节点与 $\begin{matrix} X \end{matrix}$ 轴偏移的角度。

	Figure Option View Download New Window
	图3 余弦载荷分布简图Fig.3 Cosine load distribution

1.3 求解设置

求解方式设置为几何非线性, 分析类型为静态分析。收敛准则采用力的收敛, 收敛精度可放宽至5%, 以提高收敛速度。求解时需开启大变形选项, 载荷步设置为80, 最大载荷步为100, 最小载荷步为60。

2 赫兹接触分析

通过赫兹接触分析理论, 可以推出联合加载的接触角及接触应力的计算方法。

2.1 联合载荷下接触角的计算

假定轴承只承受轴向载荷 $\begin{matrix} F_{a}, \end{matrix}$ 根据下式^[11]:

$\begin{matrix} (\frac{cosα}{cosα'} - 1) si n^{\frac{2}{3}} α' = \frac{c}{2 f_{m} - 1} (\frac{F_{a}}{Z D_{W}^{2}}) (1) \end{matrix}$

可计算加载轴向力后的接触角α ', 其中c为由接触尺寸决定的系数, 查表可得; $\begin{matrix} f_{m} \end{matrix}$ 为内、外圈平均沟道曲率半径比; $\begin{matrix} F_{a} \end{matrix}$ 代表轴向力。

利用 $\begin{matrix} α' \end{matrix}$ 计算 $\begin{matrix} tanα' / F_{a}, \end{matrix}$ 计算得出与 $\begin{matrix} F_{r} tanα' / F_{a} \end{matrix}$ 相对应的 $\begin{matrix} ε \end{matrix}$ 与 $\begin{matrix} J_{α} \end{matrix}$ 的大小, 其中 $\begin{matrix} ε \end{matrix}$ 为表示载荷区大小的变量; $\begin{matrix} J_{α} \end{matrix}$ 为轴向积分。

将上述值代入式(1)中, 便可获得计算联合加载后的接触角 $\begin{matrix} α_{c} \end{matrix}$ 的式(2), 即:

$\begin{matrix} \frac{cosα}{cosβ} - 1 = \frac{c (1 - \frac{1}{2 εco s^{2} α_{c}}) {(\frac{F_{a}}{D_{w}^{2} Z J_{α} \sin α_{c}})}^{\frac{2}{3}}}{2 f_{m} - 1} (2) \end{matrix}$

根据 $\begin{matrix} α_{c}, \end{matrix}$ 重复上述步骤迭代计算得到 $\begin{matrix} α_{c} \end{matrix}$ 的收敛值以及 $\begin{matrix} J_{α} \end{matrix}$ 与 $\begin{matrix} ε 。 \end{matrix}$

2.2 联合载荷下接触应力的计算

由 $\begin{matrix} α_{c} \end{matrix}$ 得到最大承载钢球载荷为:

$\begin{matrix} Q = \frac{F_{a}}{iZ J_{a} \sin α_{c}} (3) \end{matrix}$

式中: $\begin{matrix} i \end{matrix}$ 为轴承列数。

根据赫兹理论^[11], 最大赫兹接触应力 $\begin{matrix} P_{\max} \end{matrix}$ 为

$\begin{matrix} P_{\max} = \frac{1.5}{π e_{a} e_{b}} \times \frac{1}{ε_{E}^{2}} \sqrt[3]{{(\sum ρ)}^{2} Q} (4) \end{matrix}$

式中: $\begin{matrix} ε_{E} \end{matrix}$ 为与接触面材料的弹性模量相关的系数, 钢与钢接触时 $\begin{matrix} ε_{E} = 1; e_{a} 、 e_{b} \end{matrix}$ 是与接触椭圆长半轴 $\begin{matrix} a \end{matrix}$ 、短半轴 $\begin{matrix} b \end{matrix}$ 相关的系数; $\begin{matrix} π e_{a} e_{b} \end{matrix}$ 之值查表^[11]可得; Q为最大承载钢球的载荷; 曲率和∑ ρ =ρ _1I+ρ ₁+ρ _2I+ρ ₂, 其中ρ _1I 、ρ ₁ 、ρ _2I、ρ ₂为接触物体的主曲率, 分别是半径 $\begin{matrix} r_{1 I} 、 r_{1} 、 r_{2 I} 、 r_{2} \end{matrix}$ 的倒数, 如图4所示。

	Figure Option View Download New Window
	图4 物体与物体接触Fig.4 Object in contact with object

3 联合加载仿真分析

3.1 接触应力

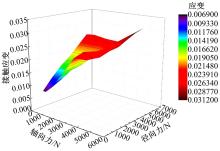
本文考虑同时施加径向力与轴向力, 研究分析轴承的应力、应变规律。为方便刻画联合加载时轴承最大接触应力与最大接触应变的变化, 从小到大均匀增大径向载荷与轴向载荷, 得到36组接触应力与接触应变值, 如表2所示。对应的应力、应变云图分别见图5和图6。

表2 加载联合载荷的接触应力应变表 Table 2 Contact parameters under combined loads

	Figure Option View Download New Window
	图5 联合加载工况下的接触应力Fig.5 Contact stress under combined loadings

	Figure Option View Download New Window
	图6 联合加载工况下的接触应变Fig.6 Contact strain under combined loading

分析表2, 再结合图5和图6可知:当施加较小的径向载荷与轴向载荷时, 随着二者的增大, 接触应力和接触应变的最大值基本呈现增大趋势; 当轴向载荷不变、径向载荷增大时, 接触应力与应变增大; 当径向载荷不变、轴向载荷增大时, 接触应力和应变增大。当轴向载荷增大到一定数值时, 应力和应变均会出现一个幅值变小的趋势, 即三维云图5和6中的凹陷处, 且随着径向载荷的持续增大, 这个趋势仍出现在较大的轴向载荷处。分析得知, 此现象的产生是由于施加径向载荷会引起附加的轴向载荷。同时, 轴向载荷也起到相应大小的预压紧力的作用, 限制轴承的移动与变形, 故接触应力与接触应变变小。

不仅如此, 一般情况下随着接触角的增大, 接触应力与应变也呈现增大趋势。而接触角的变化规律并非呈线性, 需要靠迭代计算获得。这也是本文在施加2000 N到3000 N、再到4000 N的轴向载荷的过程中, 接触应力与接触应变陡然变化的原因。

当径向载荷消失, 只存在轴向载荷时, 图7(a)(b)分别为加载100 N轴向载荷时的接触应力与接触应变图。最大接触应力为421 MPa, 最大应变为2.504× 10^-3 , 均出现在外圈滚道与滚动体的接触线上。

	Figure Option View Download New Window
	图7 施加100 N轴向载荷时的结果云图Fig.7 von Mises stress and strain diagrams under axial force 100 N

为了研究接触应力与应变随轴向载荷的变化规律, 现取不同的轴向力换算成面力加载, 得到接触参数与变化规律曲线图, 分别见表3与图8。

表3 加载轴向力接触参数 Table 3 Contact parameters under axial loads

	Figure Option View Download New Window
	图8 接触应力应变随轴向力变化曲线图Fig.8 Curves of von Mises stress and strain underaxial forces

表3给出了不同轴向载荷作用下的最大接触应力与最大接触应变, 指出了最大应力应变点出现的位置。可见, 只有施加较小轴向载荷时(≤ 500 N), 最大应力应变点才出现在外圈与滚动体接触处, 其余都出现在内圈与滚动体接触处。因此得出结论:对同一轴承结构而言, 当所受轴向载荷小于轴承极限推力载荷时, 内圈滚道与滚动体之间最大接触应力大于外圈滚道与滚动体之间的最大接触应力; 为载荷超过某一值时, 外圈滚道与滚动体之间最大接触应力大于内圈滚道与滚动体之间的最大接触应力。

图8揭示了接触应力与接触应变随轴向载荷增大的变化规律。随着轴向载荷的增大, 最大接触应力与最大接触应变值不断增大, 增大的趋势逐渐减缓。理论值与仿真结果误差较小, 验证了本文的建模方法、加载方式及求解流程的正确性与有效性。

3.2 接触角

由于接触角的变化无法直接从仿真结果获得, 因此依据本文所述赫兹接触计算, 得到对应结果, 见表4。表4揭示了联合载荷下接触角的变化规律, $\begin{matrix} A = (F_{r} tanα') / F_{a} \end{matrix}$ , 当A≥ 1时, 接触角无解, 可归为单向载荷去求解。从变化趋势可以看出:同一轴向力下随着径向力增加, 接触角大小逐渐增加; 同一径向力下随着轴向力的增加, 接触角大小逐渐减小。减小的幅度较小, 因此, 更进一步验证了前文结论, 即轴向力起到了附加的预压紧力的作用限制了轴承的变形与接触角的变化。

表4 联合载荷下接触角的变化 Table 4 Contact angle under combined loads

轴向力 /N	不同径向力下接触角/(° )
轴向力 /N	1000 N	2000 N	3000 N	4000 N	5000 N	6000 N
1000	18.619	19.946	20.167	20.734	21.210	21.629
2000	$\begin{matrix} A \geq 1 \end{matrix}$	19.359	20.087	20.659	21.164	21.583
3000	$\begin{matrix} A \geq 1 \end{matrix}$	—	19.961	20.539	21.055	21.529
4000	$\begin{matrix} A \geq 1 \end{matrix}$	$\begin{matrix} A \geq 1 \end{matrix}$	—	20.459	20.981	21.457
5000	$\begin{matrix} A \geq 1 \end{matrix}$	$\begin{matrix} A \geq 1 \end{matrix}$	$\begin{matrix} A \geq 1 \end{matrix}$	20.350	20.889	21.376
6000	$\begin{matrix} A \geq 1 \end{matrix}$	$\begin{matrix} A \geq 1 \end{matrix}$	$\begin{matrix} A \geq 1 \end{matrix}$	20.218	20.769	21.273

注:“ -” 代表求解过程无交点。

表4 联合载荷下接触角的变化 Table 4 Contact angle under combined loads

3.3 接触椭圆

滚动体与内外圈滚道的接触区域呈椭圆形, 称之为接触椭圆, 长半轴a与短半轴b之比可通过查表^[11]得到。

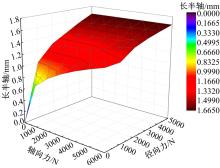
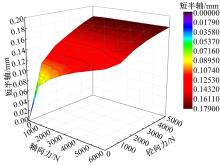
对接触面的应力图中接触椭圆测距, 得到接触椭圆的长半轴a与短半轴b的长度, 见表5。结合表5与图9、图10分析可知:随着径向力与轴向力的增大接触椭圆长半轴和短半轴都呈增大的趋势; 在径向力较小时, 轴向力的变化引起的接触椭圆的变化较大, 当径向力较大时, 轴向力的变化对接触椭圆大小的变化影响较小; 短半轴的长度约为长半轴的1/9。

表5 联合载荷下接触椭圆的变化 Table 5 Contact oval under combined loads

轴向力 /N	不同径向力下长半轴长度 $\begin{matrix} a \end{matrix}$ /mm						不同径向力下短半轴长度 $\begin{matrix} b \end{matrix}$ /mm
轴向力 /N	1000 N	2000 N	3000 N	4000 N	5000 N	6000 N	1000 N	2000 N	3000 N	4000 N	5000 N	6000 N
0	0	1.002	1.262	1.402	1.543	1.662	0	0.107	0.135	0.151	0.166	0.178
1000	0.716	1.045	1.269	1.409	1.560	1.663	0.077	0.111	0.136	0.152	0.168	0.179
2000	0.902	1.072	1.272	1.415	1.571	1.663	0.097	0.115	0.136	0.153	0.169	0.179
3000	1.032	1.091	1.276	1.423	1.581	1.663	0.111	0.117	0.137	0.155	0.170	0.179
4000	1.137	1.172	1.351	1.429	1.590	1.664	0.122	0.126	0.145	0.156	0.171	0.179
5000	1.224	1.242	1.417	1.490	1.599	1.664	0.131	0.134	0.153	0.160	0.172	0.179
6000	1.301	1.306	1.462	1.545	1.607	1.664	0.140	0.141	0.156	0.166	0.173	0.179

表5 联合载荷下接触椭圆的变化 Table 5 Contact oval under combined loads

	Figure Option View Download New Window
	图9 联合加载工况下的接触椭圆长半轴aFig.9 Contact ellipse semi-major axis a under combined loads

	Figure Option View Download New Window
	图10 联合加载工况下的接触椭圆短半轴bFig.10 Contact ellipse semi-minor axis b under combined loads

4 结论

(1)同时施加径向载荷与轴向载荷, 更贴近角接触球轴承的实际运转工况。这种联合加载产生的应力、应变, 虽然总体呈现随载荷增大而增大的趋势, 但在加大载荷过程中, 会产生应力应变不仅不会上升, 而且还会出现小幅下降的现象, 这是由施加径向载荷所引起附加的轴向载荷及接触角变化造成的, 在一定意义上, 轴向力也会起到相应大小预紧力的作用, 限制轴承的移动与变形, 使得接触应力与接触应变变小。当径向载荷消失, 仅轴向加载产生的应力、应变随载荷增大而增大, 增长速度由快变慢。当轴向载荷较小时, 最大接触应力点出现在滚动体与外圈滚道接触处; 随着轴向载荷增加, 该点出现在内圈与滚动体接触处。这个规律可在轴承参数化设计中得到应用。

(2)联合载荷下轴承滚动体与内、外圈的接触角随径向载荷的增大而增大, 随轴向载荷的增大而减小。滚动体与内外套圈的接触椭圆的长半轴与短半轴的长度随着径向载荷与轴向载荷的增大而增大。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Tatjana Lazovic, Mileta Ristivojevic, Radivoje Mitrovic. Mathematical model of load distribution in rolling bearing[J]. FME Transactions, 2008, 36(4): 189-196. [本文引用:1]
[2]	He Wei, Chen Yang, He Jun-chao, et al. Spherical contact mechanical analysis of roller cone drill bits journal bearing[J]. Petroleum, 2016, 2(2): 208-214. [本文引用:1]
[3]	方兵, 张雷, 曲兴田, 等. 角接触球轴承刚度理论计算与实验[J]. 吉林大学学报: 工学版, 2012, 42(4): 840-844. Fang Bing, Zhang Lei, Qu Xing-tian, et al. Theoretical and experimental research of stiffness of angular contact ball bearing[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(4): 840-844. [本文引用:1]
[4]	Liao Neng Tung, Bin Jen Fin. Ball bearing skidding under radial and axial loads[J]. Mechanism and Machine Theory, 2002, 37: 91-113. [本文引用:1]
[5]	Radoslav Tomovic. Calculation of the necessary level of external radial load for inner ring support on q rolling elements in a radial bearing with internal radial clearance[J]. International Journal of Mechanical Sciences, 2012, 60: 23-33. [本文引用:1]
[6]	Tang Zhao-ping, Sun Jian-ping. The contact analysis for deep groove ball bearing based on ANSYS[J]. Procedia Engineering, 2011, 23: 423-428. [本文引用:1]
[7]	Zhao Chun-jiang, Yu Xiao-kai, Huang Qing-xue, et al. Analysis on the load characteristics and coefficient of friction of angular contact ball bearing at high speed[J]. Tribology International, 2015, 87: 50-56. [本文引用:1]
[8]	Ricci Mario. Static load distribution in ball bearings including the effects of temperature and fit[J]. Tribology & Design, 2010, 66: 223-234. [本文引用:1]
[9]	颜诚, 张跃春, 王文, 等. 基于联合载荷的角接触球轴承轴向承载能力研究[J]. 机械强度, 2015, 37(6): 1124-1129. Yan Cheng, Zhang Yue-chun, Wang Wen, et al. Research on the axial carrying capacity of angular contact ball bearings based on combined loads[J]. Journal of Mechanical Strength, 2015, 37(6): 1124-1129. [本文引用:1]
[10]	刘显军, 洪军, 王军, 等. 联合外载荷作用下角接触球轴承内部载荷分布和变形的数值迭代计算[J]. 机床与液压, 2012, 40(3): 1-4. Liu Xian-jun, Hong Jun, Wang Jun, et al. Numerical iterative computation method for solving the internal load distribution and deformation of ball bearing under the condition of combined external load[J]. Machine Tool & Hydraulics, 2012, 40(3): 1-4. [本文引用:1]
[11]	冈本纯三. 球轴承的设计计算[M]. 北京: 机械工业出版社, 2003. [本文引用:4]

2008

0.0

... Tatjana^[1]和He等^[2]通过理论计算得到外部载荷对轴承内部载荷分布的影响 ...

2016

0.0

... Tatjana^[1]和He等^[2]通过理论计算得到外部载荷对轴承内部载荷分布的影响 ...

2012

0.0

. 2012, 42(4):840-844

Theoretical and experimental research of stiffness of angular contact ball bearing

角接触球轴承刚度理论计算与实验

Fang Bing , Zhang Lei , Qu Xing-tian

方兵, 张雷, 曲兴田

The geometry of contact deformation for the rolling elements of angular contact ball bearing was described by coordinate transformation method. The analytical expression for the stiffness of angular contact ball bearing was derived according to the Hertzian elastic contact theory. The influences of preload, contact angle, etc. on the bearing stiffness were analyzed theoretically. A test bench was developed to measure the bearing stiffness. The comparison was carried out between the theoretical analysis and the experimental results.The results show that the discrepancy between the theoretical calculation and test data was less than 10%, meeting the requirement of engineering calculation.

采用坐标变换方法建立角接触球轴承滚动体接触变形的几何关系,根据Hertz弹性体接触理论推导了角接触球轴承刚度的解析表达式。理论分析了预紧力、接触角等对轴承刚度的影响。研制了轴承刚度测试实验台,将理论分析与实验结果进行了对比,结果表明:理论计算方法与实验结果的相对误差在10%以内,能够满足工程计算的需要。

... 方兵等^[3]采用坐标变换方法建立角接触球轴承滚动体接触变形的几何关系 ...

2002

0.0

... Liao^[4]研究了施加单一载荷时接触应力与接触半径随着载荷变化而变化的规律 ...

2012

0.0

... Radoslav^[5]分析了在轴承内圈上施加径向载荷对轴承应力分布的影响,提出了相应的数学模型 ...

2011

0.0

... Tang等^[6]基于赫兹接触理论,建立了轴承有限元模型并对其施加径向载荷,仿真结果与赫兹理论的计算结果基本一致 ...

2015

0.0

... Zhao等^[7]和Ricci^[8]研究了轴承在单一轴向载荷作用下,其接触角与内外圈的接触应力随轴向载荷的变化规律 ...

2010

0.0

... Zhao等^[7]和Ricci^[8]研究了轴承在单一轴向载荷作用下,其接触角与内外圈的接触应力随轴向载荷的变化规律 ...

2015

0.0

. 2015, 37(6):1124-1129

Research on the axial carrying capacity of angular contact ball bearings based on combined loads

基于联合载荷的角接触球轴承轴向承载能力研究

Yan Cheng , Zhang Yue-chun , Wang Wen

颜诚, 张跃春, 王文

... 颜诚等^[9]以受轴向载荷时轴承承载能力的算法为基础,提出了基于联合载荷的角接触球轴承接触分析的改进算法,仿真结果表明:轴承轴向变形与轴向载荷之间、径向变形与径向载荷之间均是线性递增关系 ...

2012

0.0

. 2012, 40(3):1-4 DOI:doi:10.3969/j.issn.1001-3881.2012.03.001

Numerical iterative computation method for solving the internal load distribution and deformation of ball bearing under the condition of combined external load

联合外载荷作用下角接触球轴承内部载荷分布和变形的数值迭代计算

Liu Xian-jun , Hong Jun , Wang Jun

刘显军, 洪军, 王军

为了研究联合外载荷作用下球轴承的内部载荷分布和变形特性,提出一种基于赫兹接触理论的数值迭代计算方法。以角接触球轴承为对象,考虑在预紧力、轴向力、径向力等联合外载荷工况条件下内外圈滚道接触角的变化,以及滚珠载荷分布、载荷大小随接触角的变化,利用滚道接触角与滚珠载荷之间的关系式进行数值迭代求解,来寻找轴承受载后内部的平衡状态。通过与典型有限元分析结果的比较可以看出:所提方法不仅详细计算出了轴承内部的载荷情况,而且更为准确地分析了联合载荷对轴承变形的影响机制。搭建了模拟联合外载荷工况的轴承试验台,测量了轴承的变形,验证了该方法的正确性。

... 刘显军等^[10]的研究表明,同一轴向载荷下,增大径向载荷会使接触角减小,导致轴向变形有所减小 ...

2003

0.0

... 1 联合载荷下接触角的计算假定轴承只承受轴向载荷 Fa,根据下式^[11]: ...

... 根据赫兹理论^[11],最大赫兹接触应力 Pmax为 ...

... πeaeb之值查表^[11]可得 ...

... 3 接触椭圆滚动体与内外圈滚道的接触区域呈椭圆形,称之为接触椭圆,长半轴a与短半轴b之比可通过查表^[11]得到 ...