基于代理模型的中空轴式大型静压轴承多目标优化

引用本文

刘颖, 张凯, 于向军. 基于代理模型的中空轴式大型静压轴承多目标优化. 2017, 47(4): 1130-1137
LIU Ying, ZHANG Kai, YU Xiang-jun. Multi-objective optimization of hydrostatic bearing of hollow shaft based on surrogate model. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1130-1137 复制到剪切板

Permissions

基于代理模型的中空轴式大型静压轴承多目标优化

刘颖¹, 张凯¹, 于向军²

1.吉林大学机械科学与工程学院, 长春 130022

2.昆明学院自动控制与机械工程学院,昆明 650214

作者简介:刘颖(1976-),女,副教授.研究方向:现代机械设计及理论.E-mail:liuying99@jlu.edu.cn

基金:国家自然科学基金项目(51265020).

摘要

建立了中空轴式静压轴承的油膜仿真模型,分析了油腔包角、偏位角、油腔宽等设计参数对其承载力和液压功耗的影响规律。以主电机功率为8000 kW的大型球磨机静压轴承的承载力和液压功耗为优化目标,以静压轴承所需提供的最小载荷和轴瓦的许用应力为约束条件,提出了基于RBF(径向基函数)代理模型和多目标粒子群优化算法相结合的多目标优化设计方法,得到了Pareto最优解集,应用基于灰色关联度的TOPSIS方法选取出了最优妥协解。优化结果表明:优化后的静压轴承承载力提升了2.99 %,液压功耗降低了3.87 %,所承受工作介质重力提升了8.74 %。

关键词: 机械设计; 中空轴式静压轴承; 代理模型; 多目标优化; TOPSIS; 粒子群优化算法

中图分类号:TD453 文献标志码:A 文章编号:1671-5497(2017)04-1130-08

Multi-objective optimization of hydrostatic bearing of hollow shaft based on surrogate model

LIU Ying¹, ZHANG Kai¹, YU Xiang-jun²

1.School of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

2.School of Automatic control and Mechanical Engineering, Kunming University, Kunming 650214, China

Abstract

A simulation model of oil film of hollow shaft hydrostatic bearing is established. Simulations are carried out to analyze the effects of the oil cavity angle, deflection angle and oil cavity width on the bearing capacity and hydraulic power consumption of the hydrostatic bearing. The bearing capacity and hydraulic power consumption of a large-scale ball mill with motor power of 8000 kW are taken as the optimization objects. The constraint conditions are the minimum load provided by the hydrostatic bearing and the allowable stress of the bearing bush. A multi-objective optimization design method of the hydrostatic bearing is proposed based on the radial basis function(RBF) surrogate model and the multi-objective Particle Swarm Optimization (PSO) algorithm. The Pareto optimal solution set is obtained, and the optimal compromise solution is selected using TOPSIS method based on grey relational degree. Optimization results show that the optimized capacity of the hydrostatic bearing is increased by 2.99%, the hydraulic power consumption is reduced by 3.87%, and the weight of the working medium in the shell of the ball mill is reduced by 8.74%.

Keyword: mechanical design; hollow shaft hydrostatic bearing; surrogate model; multi-objective optimization; technique for order preference by similarity to an ideal solution(TOPSIS); particle swarm optimization(PSO) algorithm

Show Figures

0 引言

球磨机广泛用于选矿、建材及化工等行业。为了提高生产效率, 球磨机大型化成为发展趋势。球磨机的大型化发展对支撑其安全运行静压轴承提出了更高的要求。

针对静压轴承的设计和优化问题, 邵俊鹏等^[1]利用有限体积法, 分析了在转速、腔深及有效承载面积相同时, 扇形腔和椭圆形腔重型静压轴承油膜的压力场和温度场, 并对轴瓦和油腔结构进行了优化设计。朱希玲^{[2, 3]}分别以承载能力最大和油泵功率消耗最小为目标函数, 对球磨机静压轴承的油腔结构及轴瓦结构进行了优化设计。Kumar等^[4]和Dwivedi^[5]利用有限差分法分析了阻尼系数、油膜刚度与节流器设计参数的关系, 研究了油腔长度、宽度和油腔数量变化对静压轴承承载能力和流体流动系数的影响。Sharma等^{[6, 7]}采用有限元法对静压推力轴承特性做了计算, 分析了油腔形状对轴承性能的影响, 结果表明油腔形状对该静压轴承的刚度、承载等性能有很大的影响。

本文以主电机功率为8000 kW的大型球磨机静压轴承为研究对象, 建立了静压轴承油膜仿真模型, 通过缩比球磨机的静压轴承试验验证了静压轴承油膜仿真的准确性。分析了油腔结构对静压轴承承载力和液压功耗的影响规律。在兼顾计算精度和效率的同时, 以承载力和液压功耗为目标函数, 利用油膜的流体动力学仿真结果建立了RBF代理模型, 提出了基于粒子群优化(Particle swarm optimization, PSO)算法的大型球磨机静压轴承的多目标优化方法。

1 静压轴承仿真模型

1.1 模型简化

中空轴式静压轴承主要由中空轴、轴瓦、腰鼓形轴承衬体组成。静压轴承通过一个专用的液压泵站将具有一定压力的润滑油压进轴承的油腔内, 润滑油沿轴向及周向封油边流出, 形成具有压力分布的润滑油膜, 使中空轴浮升以承受外载荷, 形成液体静压轴承的承载力, 简化模型如图1所示。

	Figure Option View Download New Window
	图1 中空轴式静压轴承的简化模型Fig.1 Simplified model of hollow shaft hydrostatic bearing

模型中的中空轴外径为3000 mm, 内径为2520 mm, 轴承衬体厚度为260 mm, 油膜最小厚度取0.2 mm, 偏心率为ε 为0.5, 轴承包角取120° , 主轴承宽度为750 mm。

轴承内部流场中的润滑油视为定常流动的不可压缩层流流体, 油膜的质量力忽略不计, 不考虑因摩擦引起的润滑油黏度变化。

为了使供油系统获得所需的压力和流量, 油泵的输入功率N_p可由下式计算:

$\begin{matrix} N_{p} = 10^{- 7} P_{o} Q_{p} / (6 η) (1) \end{matrix}$

式中:P_o为油泵的额定输出压力, Pa; Q_p为油泵的额定输出流量, L/min; η 为油泵的效率。

静压轴承的轴瓦材料为高铅青铜IBz-34, 轴瓦的屈服极限为135 MPa, 安全系数为3.0, 因此轴瓦的许用应力为45 MPa。

1.2 边界条件

润滑油型号为N220, 动力黏度η ₄₀_°为0.195 Pa· s。为求解计算而设置的边界条件为:静压轴承进油口设为压力入口(P_inlet=P₀), 出油口设为压力出口(P_outlet=0), 中空轴表面油膜设为旋转面, 角速度ω =1.3188 rad/s, 轴瓦表面油膜设为无滑移边界。

由于静压轴承油膜网格长径比非常大, 利用几何实体进行网格划分会导致网格随着实体变形而产生错误。因此, 油膜的有限元模型需要使用旋转面网格和拉伸面网格的方法直接建立, 油膜有限元模型如图2所示。

	Figure Option View Download New Window
	图2 油膜有限元模型Fig.2 Finite element model of oil film

1.3 静压轴承仿真方法验证

由于所研究的球磨机整体尺寸巨大, 中空轴直径达3000 mm。因此, 利用小型球磨机试验台完成了静压轴承的承载试验, 试验台的静压轴承轴瓦宽150 mm, 中空轴半径为300 mm, 如图3所示。

	Figure Option View Download New Window
	图3 球磨机试验台Fig.3 Ball mill test bench

根据静压轴承的结构尺寸建立油膜的仿真模型, 通过对油膜仿真模型的简化和边界条件的设定, 利用流体计算软件得到静压轴承油膜压力仿真结果。空载静止和满载静止工况下, 静压轴承油膜压力的仿真结果与试验对比如表1所示。

表1 静压轴承油膜压力仿真结果与试验结果对比 Table 1 Comparison of simulation results and test results of hydrostatic bearing

从表1中可见, 静压轴承油腔部分油膜压力的仿真结果与试验结果基本一致, 这说明静压轴承模型简化方法和仿真方法是准确的。

2 油腔结构对静压轴承影响规律分析

2.1 油腔结构对静压轴承承载力影响规律分析

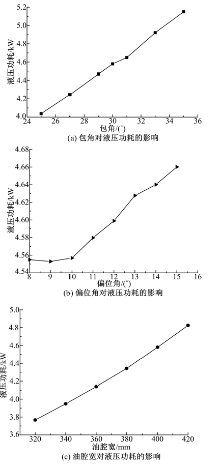
静压轴承油腔结构对其承载能力、液压功耗有很大影响。本文针对油腔包角、油腔偏位角以及油腔宽3方面对静压轴承的承载力和液压功耗采用流体计算软件(FLUENT)进行了仿真, 其中包角、偏位角和油腔宽的选取通过企业调研得到。油腔包角、偏位角及宽度对静压轴承承载力的影响规律如图4所示。

	Figure Option View Download New Window
	图4 油腔结构对承载力影响Fig.4 Effect of oil cavity structure on bearing capacity

由图4(a)可见, 静压轴承的承载力随油腔包角的增大而增大; 由图4(b)可见, 油腔偏位角为8° ~10° , 承载力变化较小, 偏位角大于10° 后, 承载力开始显著地变小; 由图4(c)可见, 静压轴承的承载力随油腔宽的增大而增大。

2.2 油腔结构对静压轴承液压功耗影响规律分析

油腔结构对静压轴承液压功耗的影响规律如图5所示。由图5(a)可见, 静压轴承的液压功耗随油腔包角的增大而增大; 由图5(b)可见, 油腔偏位角为8° ~10° , 液压功耗变化较小, 偏位角大于10° 后, 液压功耗开始显著变大; 由图5(c)可见, 静压轴承的液压功耗随油腔宽的增大而增大。

	Figure Option View Download New Window
	图5 油腔结构对液压功耗的影响Fig.5 Effect of oil cavity structure on hydraulic power consumption

3 静压轴承优化设计

通过油腔结构对静压轴承影响规律进行分析发现, 静压轴承的轴承承载性能和液压功耗是相互制约的关系, 因此为了能够在原设计的基础上在提高轴承承载性能的同时使得液压功耗得到最大限度的降低, 需要对轴承结构进行优化设计。油腔结构对静压轴承影响规律是优化变量的选取以及RBF代理模型确定的基础。

3.1 优化目标

选取静压轴承的承载力和液压功耗为优化目标。实际工程中可以用承载力、液压功耗或二者折中为评价静压轴承性能的准则, 考虑到这种评估准则的不确定性, 应用以下优化方案来提高静压轴承优化设计的鲁棒性^[8]。

方案1 静压轴承的承载能力F_f最大。

$\begin{matrix} \{\begin{matrix} \min - F_{f} (x) \\ s . t . F_{c} (x) \leq F_{c 0} = 45 \\ x_{L} \leq x \leq x_{U} \end{matrix} (2) \end{matrix}$

方案2 静压轴承的液压功耗F_p最小。

$\begin{matrix} \{\begin{matrix} \min F_{p} (x) \\ s . t . F_{f} (x) \geq F_{f 0} = 6287 \\ F_{c} (x) \leq F_{c 0} = 45 \\ x_{L} \leq x \leq x_{U} \end{matrix} (3) \end{matrix}$

方案3 静压轴承的承载力F_f和液压功耗F_p达到相对最优。

$\begin{matrix} \{\begin{matrix} \min \{- F_{f} (x), F_{p} (x)\} \\ s . t . F_{f} (x) \geq F_{f 0} = 6287 \\ F_{c} (x) \leq F_{c 0} = 45 \\ x_{L} \leq x \leq x_{U} \end{matrix} (4) \end{matrix}$

式中:F_c0为轴瓦许用应力; F_c(x)为轴瓦所受的最大应力; x_L、x_U分别为静压轴承设计变量的下边界和上边界; F_f0为静压需要承受的最大载荷; x为设计变量 (包角、偏位角、油腔宽)。

3.2 静压轴承最优妥协解

多目标优化问题中各个目标之间没有统一的量纲和度量标准, 无法找出所有目标函数都是最优的解, 因此, 只能找出相对最优的解。本文利用基于灰色关联度的TOPSIS^[9](Technique for order preference by similarity to ideal solution)方法, 从Pareto最优解集中挑选静压轴承优化的最优妥协解。挑选最优妥协解方法如下:

设初始决策矩阵X= $\begin{matrix} [x_{ij}]_{m \times n} \end{matrix}$ , 其中x_ij为在第i个Pareto解的第j个目标函数值, i∈ m, j∈ n, 本文中目标函数有两个, 即n=2。ω _j为第j个目标函数的权向量, 满足 $\begin{matrix} \overset{2}{\sum_{j = 1}} \end{matrix}$ ω _j=1, ω _j≥ 0。

用向量规范化法构造规范化决策矩阵Y= $\begin{matrix} [y_{ij}]_{m \times n} \end{matrix}$ , 如式(5)所示:

$\begin{matrix} y_{ij} = x_{ij} / \sqrt[]{\overset{m}{\sum_{i = 1}} x_{ij}^{2}} (5) \end{matrix}$

建立加权规范化决策矩Z= $\begin{matrix} [z_{ij}]_{m \times n} \end{matrix}$ , 其中z_ij=ω _jy_ij。

分别建立静压轴承多目标优化的正理想解z⁺和负理想解z^-, 如式(6)所示:

$\begin{matrix} \{\begin{matrix} z^{+} = (\min_{\forall i} z_{i 1}, \min_{\forall i} z_{i 2}) \\ z^{-} = (\max_{\forall i} z_{i 1}, \max_{\forall i} z_{i 2}) \end{matrix} (6) \end{matrix}$

分别计算各方案与正理想解的灰色关联系数矩阵R⁺= $\begin{matrix} [r_{ij}^{+}]_{m \times n} \end{matrix}$ , 与负理想解的灰色关联系数矩阵R^-= $\begin{matrix} [r_{ij}^{-}]_{m \times n} \end{matrix}$ ; 则灰色关联系数 $\begin{matrix} r_{ij}^{+} \end{matrix}$ 和 $\begin{matrix} r_{ij}^{-} \end{matrix}$ 如式(7)所示:

$\begin{matrix} \{\begin{matrix} r (z_{j}^{+}, z_{ij}) = \\ \frac{\min_{\forall i} \min_{\forall j} |z_{j}^{+} - z_{ij}| + ε \max_{\forall i} \max_{\forall j} |z_{j}^{+} - z_{ij}|}{|z_{j}^{+} - z_{ij}| + ε \max_{\forall i} \max_{\forall j} |z_{j}^{+} - z_{ij}|} \\ r (z_{j}^{-}, z_{ij}) = \\ \frac{\min_{\forall i} \min_{\forall j} |z_{j}^{-} - z_{ij}| + ε \max_{\forall i} \max_{\forall j} |z_{j}^{-} - z_{ij}|}{|z_{j}^{-} - z_{ij}| + ε \max_{\forall i} \max_{\forall j} |z_{j}^{-} - z_{ij}|} \end{matrix} (7) \end{matrix}$

式中:ε ∈ (0, 1)为分辨系数, 本文中取为0.5。

计算正理想解和负理想解与各方案的灰色关联度 $\begin{matrix} r_{i}^{+} \end{matrix}$ 和 $\begin{matrix} r_{i}^{-} \end{matrix}$ , 如下所示:

$\begin{matrix} r_{i}^{+} = \frac{1}{2} \overset{2}{\sum_{j = 1}} r_{ij}^{+}, r_{i}^{-} = \frac{1}{2} \overset{2}{\sum_{j = 1}} r_{ij}^{-} (8) \end{matrix}$

构造方案的灰色关联相对贴近度C_i, 如下式所示:

$\begin{matrix} C_{i} = \frac{r_{i}^{+}}{r_{i}^{+} + r_{i}^{-}} (9) \end{matrix}$

式中:0< $\begin{matrix} r_{i}^{+} \end{matrix}$ < 1, 0< $\begin{matrix} r_{i}^{-} \end{matrix}$ < 1。因此, 灰色关联相对贴近度0< C_i< 1。

按照C_i的大小对静压轴承多目标优化方案进行排序, 其中C_i越大, 方案越优; 反之, 方案越差。

3.3 试验设计

建立代理模型^[10]必须先确定优化设计变量及取值范围。本文选取的3个优化变量初值及范围如表2所示。其中x₁为静压轴承油腔的包角, x₂为静压轴承油腔的偏位角, x₃为静压轴承油腔的宽度。

表2 优化变量初值及取值范围 Table 2 Initial value and range of optimization variables

利用优化的拉丁超立方法(Optimal latin hypercube design-OLHD)设计RBF模型的试验方案。构建RBF模型所需最少样本点为2n+1个, n为3个设计变量。综合考虑RBF模型所需样本点要求和计算成本, 本文采用OLHD方法设计的20组试验数据作为构建RBF模型的初始样本点, 10组试验数据作为RBF模型的检验样本点。试验方案及试验结果如表3所示。

表3 OLHD试验方案及试验结果 Table 3 OLHD test scheme and test results

3.4 RBF模型的建立和误差分析

RBF模型能够很好地平衡非线性近似精度和计算效率问题, 其基本形式如下。

$\begin{matrix} \begin{matrix} f (x) = \overset{n}{\sum_{i = 1}} [α_{i} ψ_{i} (x)] + α_{n + 1} (10) \\ i = 1, 2, \dots, n \end{matrix} \end{matrix}$

式中:α _i为线性叠加权系数; n为样本点个数; ψ _i(x)为径向函数, 其形式如下:

$\begin{matrix} ψ_{i} (x) = ‖ x - x_{i} ‖^{c} (11) \end{matrix}$

式中:c是形状参数, c∈ (0.2, 3.0)。再给定一个限制方程 $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ α _i=0, 进而可求出该插值函数系数矩阵。

代理模型是一种设计变量与响应函数之间的近似关系式, 替代真实模型之前需要对代理模型进行精度检验。本文选用均方根误差法(Root mean square error, RMSE)对RBF模型进行精度检验, RMSE检验方法定义如下:

$\begin{matrix} RMSE = \sqrt[]{\frac{\overset{k}{\sum_{i = 1}} (y_{i} - {\hat{y}}_{i})}{k}} (12) \end{matrix}$

式中:k是样本点数量; $\begin{matrix} {\hat{y}}_{i} \end{matrix}$ 是y_i的预测值。RMSE的值小于0.2即符合精度检验要求, 其值越趋近于0说明代理模型的精度越高。

经检验RBF模型的承载能力、液压功耗和轴瓦最大应力的均方根误差分别为:0.00664、0.01642和0.03114。符合精度检验要求, RBF模型可以做为静压轴承的代理模型。

3.5 优化结果

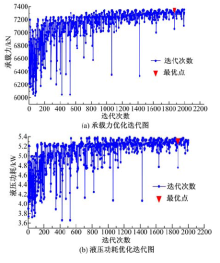
方案1以静压轴承的承载力为目标函数, 应用多岛遗传算法得到的承载力和液压功耗迭代过程如图6(a)和图6(b)所示。

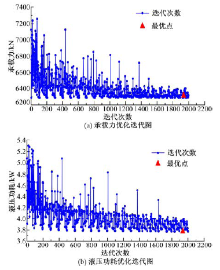
	Figure Option View Download New Window
	图6 方案一优化迭代图Fig.6 Iteration graph of optimization process for scheme 1

方案2以静压轴承的液压功耗为目标函数, 应用多岛遗传算法得到的承载力和液压功耗迭代过程如图7(a)和图7(b)所示。

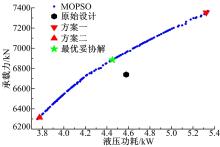
	Figure Option View Download New Window
	图7 方案二优化迭代图Fig.7 Iteration graph of optimization process for scheme 2

利用MOPSO多目标优化算法^{[11, 12]}获得的静压轴承多目标优化Pareto最优解集如图8所示。从图8中可以看出静压轴承的单目标优化最优解值非常接近Pareto最优解集的两个端点。静压轴承优化前、后油膜压力场的对比如图9所示, 优化后的油腔比优化前的包角要大, 偏位角要小, 油腔宽度要小。优化前、后静压轴承变量及目标值的对比如表4所示, 其中N表示球磨机的工作介质重力。

	Figure Option View Download New Window
	图8 Pareto最优解集Fig.8 Pareto optimal solution set

	Figure Option View Download New Window
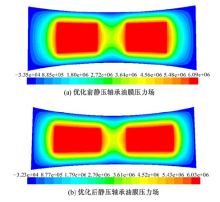	图9 优化前后静压轴承油膜压力场对比图Fig.9 Comparison of oil film pressure field of hydrostatic bearing before and after optimization

由表4可知, 虽然方案1和方案2分别得到静压轴承的承载力和液压功耗的最优解, 但是两个方案另一个目标都要比优化前的性能差。方案3优化后的轴承承载能力要比优化前提升了2.99%, 液压功耗比优化前降低了3.87%。球磨机自身重力是不变的, 所以优化后轴承提升的承载力将用于提升球磨机工作介质的重力。又由于球磨机是由两个静压轴承支撑的, 优化后球磨机的额定工作介质提升了402 kN, 原始设计中工作介质的总重力为4600 kN。因此, 优化后的静压轴承比优化前多承受8.74%的工作介质重力。

表4 优化前、后变量及目标值的对比 Table 4 Comparison of variables and optimal objects before and after optimization

4 结论

(1)以某大型球磨机静压轴承为研究对象, 建立了静压轴承油膜流体动力学仿真模型, 分析了油腔包角、油腔宽和油腔偏位角对静压轴承承载力及液压功耗的影响规律。

(2)将代理模型和多目标粒子群优化算法相结合, 对静压轴承进行了多目标优化设计, 得到了Pareto最优解集。

(3)采用基于灰色关联度的TOPSIS方法选取静压轴承多目标优化的最优妥协解, 结果表明:优化后的静压轴承承载力提升了2.99%, 液压功耗降低了3.87%, 工作介质重力提升了8.74%。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	邵俊鹏, 张艳芹, 韩桂华, 等. 重型静压轴承油腔结构优化与流场仿真[J]. 系统仿真学报, 2010, 22: 1093-1096. Shao Jun-peng, Zhang Yan-qin, Han Gui-hua, et al. Oil recess structure optimization and flow simulation for heavy hydrostatic bearing[J]. Journal of System Simulation, 2010, 22: 1093-1096. [本文引用:1]
[2]	朱希玲. 基于ANSYS的静压轴承油腔结构优化设计[J]. 轴承, 2009(7): 12-15. Zhu Xi-ling. Optimum design of oil recess used in hydrostatic bearing based on ANSYS[J]. Bearing, 2009(7): 12-15. [本文引用:1]
[3]	朱希玲. 球磨机静压轴承轴瓦结构优化设计[J]. 润滑与密封, 2009, 34(7): 88-90. Zhu Xi-ling. Optimum design of hydrostatic bearing bushing structure used in ball-grinding mil[J]. Lubrication and Seal, 2009, 34(7): 88-90. [本文引用:1]
[4]	Kumar V, Sharma S C, Jain S C. On the restrictor design parameter of hybrid journal bearing for optimum rotordynamic coefficients[J]. Tribology International, 2006, 39(4): 356-368. [本文引用:1]
[5]	Dwivedi V K, Chand S, Pand ey K N. Effect of number and size of recess on the performance of hybrid (hydrostatic/hydrodynamic) journal bearing[J]. Procedia Engineering, 2013, 51: 810-817. [本文引用:1]
[6]	Yadav S K, Sharma S C. Performance of hydrostatic tilted thrust pad bearings of various recess shapes operating with non-Newtonian lubricant[J]. Finite Elements in Analysis & Design, 2014, 87: 43-55. [本文引用:1]
[7]	Sharma S C, Rajput A K. Effect of geometric imperfections of journal on the performance of micropolar lubricated 4-pocket hybrid journal bearing[J]. Tribology International, 2013, 60(7): 156-168. [本文引用:1]
[8]	张凯. 基于代理模型的大型球磨机静压轴承结构优化[D]. 长春: 吉林大学机械科学与工程学院, 2016. Zhang Kai. Structural optimization of hydrostatic bearing of large-type ball mill based on surrogate model[D]. Changchun: College of Mechnical Science and Engineering, Jilin University, 2016. [本文引用:1]
[9]	Fang J, Gao Y, Sun G, et al. Multi-objective robust design optimization of fatigue life for a truck cab[J]. Reliability Engineering & System Safety, 2015, 135: 1-8. [本文引用:1]
[10]	左曙光, 蒋维旭, 吴旭东, 等. 基于ISIGHT的电动汽车扭杆梁悬架振动传递特性优化[J]. 吉林大学学报: 工学版, 2015, 45(5): 1381-1387. Zuo Shu-guang, Jiang Wei-xu, Wu Xu-dong, et al. Vibration transfer characteristics optimization of an electric vehicle's twist beam suspension based on ISIGHT[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(5): 1381-1387. [本文引用:1]
[11]	蒋荣超, 王登峰, 秦民, 等. 基于疲劳寿命的轿车后悬架扭转梁轻量化设计[J]. 吉林大学学报: 工学版, 2016, 46(1): 35-42. Jiang Rong-chao, Wang Deng-feng, Qin Min, et al. Lightweight design of twist beam of rear suspension of passenger car based on fatigue life[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(1): 35-42. [本文引用:1]
[12]	Cooren Y, Clerc M, Siarry P. MO-TRIBES, an adaptive multiobjective particle swarm optimization algorithm[J]. Computational Optimization & Applications, 2011, 49(2): 379-400. [本文引用:1]

2010

0.0

. 2010, 22:1093-1096

Oil recess structure optimization and flow simulation for heavy hydrostatic bearing

重型静压轴承油腔结构优化与流场仿真

Shao Jun-peng , Zhang Yan-qin , Han Gui-hua

邵俊鹏, 张艳芹, 韩桂华

针对重型静压轴承油腔结构优化问题,利用有限体积法,模拟了扇形腔和椭圆形腔间隙流体的压力场和温度场,并建立了旋转坐标系下的控制方程,探讨了在转速、腔深及有效承载面积相同时两种腔形的压力及温度分布规律,优化了油腔结构.结果表明:两种腔形润滑性能有所不同,椭圆形腔最大压力分布区域较扇形腔大,承载能力强,但由于椭圆形油腔油膜剪切面积较大导致椭圆形腔温度分布较扇形腔高.数值计算结果真实反应了轴承内部流态,仿真结果为工程实际轴承油腔结构优化设计提供了理论依据.

... 针对静压轴承的设计和优化问题,邵俊鹏等^[1]利用有限体积法,分析了在转速、腔深及有效承载面积相同时,扇形腔和椭圆形腔重型静压轴承油膜的压力场和温度场,并对轴瓦和油腔结构进行了优化设计 ...

2009

0.0

... 朱希玲^[2,3]分别以承载能力最大和油泵功率消耗最小为目标函数,对球磨机静压轴承的油腔结构及轴瓦结构进行了优化设计 ...

2009

0.0

. 2009, 34(7):88-90 DOI:doi:10.3969/j.issn.0254-0150.2009.07.022

Optimum design of hydrostatic bearing bushing structure used in ball-grinding mil

球磨机静压轴承轴瓦结构优化设计

Zhu Xi-ling.

朱希玲

基于ANSYS有限元软件对轴瓦结构进行了优化设计.在给定条件下,以油泵的功率消耗最小为目标函数,对油腔的结构参数进行优化.结果表明,采用优化后的油腔结构参数,油泵的功率消耗可以减少6.23%.在静压轴承设计中,采用ANSYS进行优化设计,可以实现柔性设计. Abstract： The structure of bushing was optimized with ANSYS software. Under given constraint conditions, by consider-ing minimum oil pump power as the objective function, optimum design on the oil recess structure parameter was done. The result indicates that oil pump power can decrease 6. 23 percent if optimized design data was used. Flexibility design is ful-filled in the optimum design of hydrostatic bearing with ANSYS software.

... 朱希玲^[2,3]分别以承载能力最大和油泵功率消耗最小为目标函数,对球磨机静压轴承的油腔结构及轴瓦结构进行了优化设计 ...

2006

0.0

... Kumar等^[4]和Dwivedi^[5]利用有限差分法分析了阻尼系数、油膜刚度与节流器设计参数的关系,研究了油腔长度、宽度和油腔数量变化对静压轴承承载能力和流体流动系数的影响 ...

2013

0.0

2014

0.0

... Sharma等^[6,7]采用有限元法对静压推力轴承特性做了计算,分析了油腔形状对轴承性能的影响,结果表明油腔形状对该静压轴承的刚度、承载等性能有很大的影响 ...

2013

0.0

2016

0.0

. 2016, :-

Structural optimization of hydrostatic bearing of large-type ball mill based on surrogate model

基于代理模型的大型球磨机静压轴承结构优化[D]

Zhang Kai.

张凯

近年来为了提高生产效率,球磨机型号不断扩大,并经常处于连续低速重载这样十分恶劣的工作环境,静压轴承的性能直接影响到球磨机安全性。因此研究静压轴承的承载性能、功率损耗和静压轴承的优化设计对保证球磨机的安全性、提高生产效率和经济性能具有重要意义。本文结合国家自然科学基金项目(51265020),通过对静压轴承油膜的研究,讨论分析了油腔形状及其结构参数对静压轴承承载性能和功率损耗的影响规律,并做了静压轴承的试验测试,最后对静压轴承的结构参数进行了优化设计。主要研究工作和结论如下:介绍大型球磨机静压轴承的结构特点与材质,并总结了静压轴承性能的影响因素。通过利用CFD仿真技术分析油腔形状、油腔包角、油腔宽和油腔偏位角对静压轴承承载能力、液压功耗及压力场的影响,为验证仿真方法的准确性,进行试验静压轴承的测试。结果表明油腔结构参数对静压轴承的性能有较大影响,并且试验结果证明仿真方法的准确性。提出构建静压轴承油膜代理模型的方法。通过使用优化的拉丁超立方设计试验方案,分别采用RSM方法、Kriging方法和RBF方法建立代理模型,并对三种代理模型做了精度检验和对比分析。结果表明RBF模型更适合做为静压轴承油膜的代理模型,为下一步静压轴承的结构优化打下基础。对大型球磨机静压轴承结构进行了优化设计。在满足轴承工作载荷的要求下,基于RBF代理模型分别应用MIGA优化算法对轴承进行单目标优化和MOPSO优化算法对轴承进行多目标优化,并通过应用基于灰色关联度的TOPSIS方法选取Pareto解集最优妥协解。最后将优化后的结果与原始设计进行对比分析。结果表明单目标优化设计只能使得轴承的一个目标优于原始设计,而多目标优化设计的静压轴承相比单目标优化设计和原始设计的静压轴承性能更好,不但可以承受更多的工作介质重量,而且有效降低了轴承的功率损耗。本文通过对大型球磨机静压轴承油膜进行CFD仿真计算,得到了静压轴承的承载力、功率损耗及油膜的压力分布规律,并基于代理模型对静压轴承结构进行了优化设计,对提高大型球磨机的安全性、生产效率和节约能耗具有重要意义。

... 实际工程中可以用承载力、液压功耗或二者折中为评价静压轴承性能的准则,考虑到这种评估准则的不确定性,应用以下优化方案来提高静压轴承优化设计的鲁棒性^[8] ...

2015

0.0

... 本文利用基于灰色关联度的TOPSIS^[9](Technique for order preference by similarity to ideal solution)方法,从Pareto最优解集中挑选静压轴承优化的最优妥协解 ...

2015

0.0

. 2015, 45(5):1381-1387 DOI:doi:10.13229/j.cnki.jdxbgxb201505001

Vibration transfer characteristics optimization of an electric vehicle's twist beam suspension based on ISIGHT

基于ISIGHT的电动汽车扭杆梁悬架振动传递特性优化

Zuo Shu-guang , Jiang Wei-xu , Wu Xu-dong

左曙光, 蒋维旭, 吴旭东

An optimization method was proposed to solve the vibration issue of suspension system in both vertical and longitude directions, which is commonly caused by torque ripple of wheel-drive motor in electric vehicle. By flexibly modeling of the twist beam and realizing the high-frequency bushing model in the ADAMS, the elastic component was accurately described, then, the high-frequency applied suspension model was built. Based on ISIGHT software, the multi-objective optimization was conducted by integrating multi-disciplinary software. The optimization results showed that the weighted area of longitudinal vibration transfer function was optimized by 17.23% with slightly reducing the weighted area of vertical vibration transfer function. Within the target spectrum, the optimizing effect of vibration transfer is significant.

针对车用驱动电机转矩波动引起悬架系统振动进而造成车内噪声的问题,提出通过改善悬架纵向和垂向振动传递特性来实现减振的优化方法。通过扭杆梁柔性化、高频衬套模型的ADAMS实现等措施保证悬架弹性元件的精确描述来建立适用于高频仿真的悬架模型,并基于此模型进行振动传递特性分析,最后基于ISIGHT集成多学科软件实现多目标全局优化。优化结果表明:在略微减小垂向振动传递函数加权面积的基础上使纵向振动传递函数加权面积减小了17.23%,且在目标频段内振动传递优化效果显著。

... 3 试验设计建立代理模型^[10]必须先确定优化设计变量及取值范围 ...

2016

0.0

. 2016, 46(1):35-42 DOI:doi:10.13229/j.cnki.jdxbgxb201601006

Lightweight design of twist beam of rear suspension of passenger car based on fatigue life

基于疲劳寿命的轿车后悬架扭转梁轻量化设计

Jiang Rong-chao , Wang Deng-feng , Qin Min

蒋荣超, 王登峰, 秦民

This paper studies the lightweight design method of the twist beam of rear suspension of a domestic passenger car. The whole vehicle's rigid-flexible coupling model with flexible twist beam was built using multi-body dynamics software. Modal test of the twist beam in a free-free configuration and vehicle road test of ride comfort were carried out to verify the validity of the proposed model. On this basis, the modal displacement time history of the twist beam was calculated from a dynamic simulation on the durability enhancement road. Then the stress time history of the twist beam was obtained based on Modal Stress Recovery (MSR). According to the nominal stress method, fatigue life of the twist beam was assessed. Furthermore, mesh morphing technology was employed to build the parametric model of the twist beam, which was used to define the design variables. Then, the Kriging approximation model and particle swarm algorithm were adopted to perform the multi-objective optimization of the twist beam. The mass and fatigue life were defined as the objective functions, while the first modal frequency and torsional stiffness were taken as the constraints. The Pareto optimal set was found and one of the optimal solutions was chosen to check the effectiveness of the optimization method. The results indicate that the weight of the optimized twist beam is reduced 20.35% while its fatigue life satisfies the design requirement.

以某国产轿车后悬架扭转梁的轻量化为研究目标,利用多体动力学软件建立考虑后悬架扭转梁柔性的整车刚柔耦合模型,并通过扭转梁自由模态试验和整车行驶平顺性实车道路试验验证了模型的正确性。在耐久性强化路面上进行整车动力学仿真分析,计算扭转梁模态位移时间历程,通过模态应力恢复得到扭转梁应力时间历程,并采用名义应力法进行疲劳寿命分析。基于网格变形技术建立扭转梁参数化模型并定义设计变量,以质量和疲劳寿命为优化目标,以一阶扭转模态频率和扭转刚度为约束条件,结合Kriging近似模型和多目标粒子群优化算法对扭转梁进行多目标优化设计,获取Pareto最优解集,并选取一个最优解验证扭转梁轻量化效果。结果表明,在使疲劳寿命满足设计要求的同时,优化后扭转梁质量减少20.35%,轻量化效果比较明显。

... 利用MOPSO多目标优化算法^[11,12]获得的静压轴承多目标优化Pareto最优解集如图8所示 ...

2011

0.0

... 利用MOPSO多目标优化算法^[11,12]获得的静压轴承多目标优化Pareto最优解集如图8所示 ...