基于波纹梁的两自由度低频振动能量收集装置

引用本文

王海, 姚刚, 邱皖群, 杨春来, 付邦晨. 基于波纹梁的两自由度低频振动能量收集装置. 2017, 47(4): 1144-1148
WANG Hai, YAO Gang, QIU Wan-qun, YANG Chun-lai, FU Bang-chen. Performance-enhanced two-degree-of-freedom energy harvester for low frequency vibration utilizing corrugated cantilever beam. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1144-1148 复制到剪切板

Permissions

基于波纹梁的两自由度低频振动能量收集装置

王海, 姚刚, 邱皖群, 杨春来, 付邦晨

安徽工程大学机械与汽车工程学院,安徽芜湖 241000

作者简介:王海(1976-),男,教授,博士.研究方向:微机械.E-mail:wanghai.20000@163.com

基金:国家自然科学基金项目(51275001,51375469).

摘要

为改善压电式振动能量收集装置固有频率高、能量收集效率低等问题,设计了一种基于波纹梁式压电振子的两自由度振动能量收集装置,并通过理论建模和数值仿真分析其能量收集特性。分析结果表明:与传统的单自由度和两自由度压电振子相比,含有波纹梁的压电振子的固有频率最低,且前五阶固有频率均为0~60 Hz;其中,第四阶固有频率为45.92 Hz,比单自由度压电振子低419.9 Hz,比传统两自由度压电振子低55.1 Hz。同时,在相同条件下波纹梁式两自由度压电振子输出的电压最大,可达到28 V。

关键词: 机械设计; 压电能量收集; 波纹梁; 低频; 两自由度

中图分类号:TH132;TN384 文献标志码:A 文章编号:1671-5497(2017)04-1144-05

Performance-enhanced two-degree-of-freedom energy harvester for low frequency vibration utilizing corrugated cantilever beam

WANG Hai, YAO Gang, QIU Wan-qun, YANG Chun-lai, FU Bang-chen

School of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu 241000, China

Abstract

Traditional Piezoelectric Energy Harvester (PEH) has high natural frequency and low electromechanical conversion efficiency. To overcome this problem a corrugate two-degree-of-freedom (2DOF) PEH is proposed. The energy harvesting characteristics are analyzed using theoretical modeling and numerical simulation. Results show that compared to 1DOF PEH and traditional 2DOF PEH, corrugate 2DOF PEH can achieve fifth order of resonance frequency in the range of 0 to 60 Hz. The fourth resonance frequency of the corrugate 2DOF PEH is 45.92 Hz, which is 419.9 Hz lower than that of 1DOF PEH, and 55.1 Hz lower than that of traditional 2DOF PEH. Meanwhile, the output voltage of the corrugate 2DOF PEH can be controlled as high as 28 V in the same condition, which is the highest voltage among the three harvesters.

Keyword: mechanical design; piezoelectric energy harvesting; corrugated cantilevered beam; low frequency; two-degree-of-freedom

Show Figures

0 引言

随着来无线传感网络的发展, 传感器节点已被应用于环境监测、农业应用、生命健康以及交通管控等领域, 而节点供能是目前亟待解决的关键问题。传统的节点供能方式存在容量小、更换难等不足, 采用环境能量获取的方式是一种有效解决途径。目前, 能量收集方式分为压电式^{[1, 2]}、电磁式^{[3, 4]}和静电式^{[5, 6]}等, 其中压电式能量收集方式因结构简单、能量密度高、环境友好、不受电磁干扰等优点而被广泛应用于振动能量收集技术。

车辆驶过的路面、工作中的机器、运动的人体等都是环境中常见的振动源^[7], 它们振动频率约为0~250 Hz^[8], 属于低频振动。因此, 用于振动能量收集的压电振子在此范围内应有多阶谐振频率或较宽的工作频带。传统的单自由度压电振子因其结构紧凑、简单而被广泛应用, 但其仍然存在固有频率高、能量收集效率低等不足。

近年来, 为了解决此类问题国内外学者做了很多相关研究。如管青春^[9]提出一种H形质量块压电回收结构, 提高了压电片的利用率和能量收集效率。Leland等^[10]通过施加轴向预应力来改变装置的固有频率。Wu等^[11]设计了一种断路器式两自由度压电收集结构, 有效拓宽了工作频带。目前的压电能量收集装置虽然在一定程度上降低了固有频率, 但最多只有两阶谐振频率可用, 且现有的技术使用的压电材料多为脆性材料PZT, 使用寿命短。

针对以上问题, 本文设计了一种基于PVDF材料的波纹梁两自由度低频振动能量收集装置。首先, 建立波纹梁两自由度压电振子的理论模型。然后, 在理论模型的基础上利用COMSOL软件对其能量获取特性进行分析。最后, 将仿真分析的结果与传统单自由度和两自由度压电振子俘能特性进行对比。

1 压电振子的结构与理论分析

1.1 波纹梁压电振子的结构

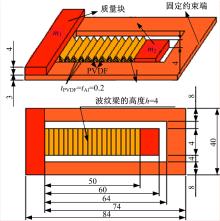
图1为波纹梁压电振子的尺寸结构图。其中, 内梁为波纹形压电双晶片梁, 由上、下两层PVDF薄膜和中间铝制基底组成; 外梁是长直的铝梁。内、外梁的自由端都附着有不同尺寸的钢块作为质量块, 且外梁的右端为固定端。

	Figure Option View Download New Window
	图1 波纹梁两自由度压电振子的结构尺寸图Fig.1 Structure of corrugated 2-DOF piezoelectric energy harvester

1.2 波纹梁压电振子的理论分析

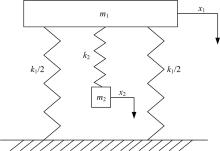
波纹梁压电振子能量收集系统可以等效为一个二阶弹簧-质量线性系统, 如图2所示, 其中, m₁ 、m₂ 分别是内、外梁上附着的钢块质量; x₁ 、x₂ 分别是m₁ 、m₂ 的位移, k₁ 、k₂表示内、外梁的刚度。

	Figure Option View Download New Window
	图2 波纹梁两自由度压电振子的简化模型Fig.2 Schematic diagram of a corrugated 2-DOF system

根据欧拉-伯努利梁理论可得波纹梁压电振子自由振动时的动力学方程如下:

$\begin{matrix} (\begin{matrix} m_{1} & 0 \\ 0 & m_{2} \end{matrix}) (\begin{matrix} {\overset{\cdot \cdot}{x}}_{1} \\ {\overset{\cdot \cdot}{x}}_{2} \end{matrix}) + (\begin{matrix} k_{1} + k_{2} & - k_{2} \\ - k_{2} & k_{2} \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix}) (1) \end{matrix}$

通过简化后可得式(1)的特征函数如下:

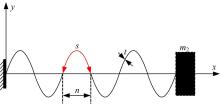
$λ^{2} - [1 + b + \frac{b}{a}] \frac{k_{1}}{m_{1}} λ + \frac{b}{a} {(\frac{k_{1}}{m_{1}})}^{2} = 0 (2)$

$\begin{matrix} \begin{matrix} k_{1} = \frac{1}{2 π} \sqrt[]{3 EI / L_{1}^{3}}, k_{2} = \frac{1}{2 π} \sqrt[]{\frac{n}{s} \frac{E t^{3}}{12 (1 - μ^{2})} \frac{3}{L_{2}^{3}}} (3) \end{matrix} \end{matrix}$

式中:无量纲参数a、b分别为m₂/m₁ 、k₂/k₁; L₁ 、L₂ 分别表示内、外梁的长度; EI表示压电振子的抗弯刚度; μ 为材料的泊松比; s为y轴正方向上的波长, 如图3所示; n是s在x轴方向上的长度, t是波纹梁的厚度。将式(3)代入式(2)中可得特征方程的根:

$\begin{matrix} \{\begin{matrix} λ_{1} = - \frac{1}{2} - \frac{\sqrt[]{{(a + ab + b)}^{2} - 4 ab}}{2 (a + ab + b)} \\ λ_{2} = - \frac{1}{2} + \frac{\sqrt[]{{(a + ab + b)}^{2} - 4 ab}}{2 (a + ab + b)} \end{matrix} (4) \end{matrix}$

最后, 可得波纹梁压电振子的固有频率为:

$\begin{matrix} ω_{1} = \sqrt[]{λ_{1}}, ω_{2} = \sqrt[]{λ_{2}} (5) \end{matrix}$

	Figure Option View Download New Window
	图3 波纹梁的简化图Fig.3 Geometry of corrugated inner beam

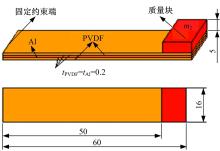
利用COMSOL软件对波纹梁压电振子进行谐响应和俘能性能分析, 验证波纹梁压电振子的低频率振动特性, 并与传统单自由度和两自由度压电振子对比。传统单自由度和两自由度压电振子的结构尺寸如图4和图5所示。

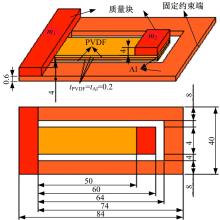	Figure Option View Download New Window
	图4 传统两自由度压电振子的结构尺寸图Fig.4 Structure and dimensions of conventional two-degree-of-freedom cantilevered beam

	Figure Option View Download New Window
	图5 传统单自由度压电振子的结构尺寸图Fig.5 Structure and dimensions of conventional single-degree-of-freedom cantilevered beam

2 数值仿真分析

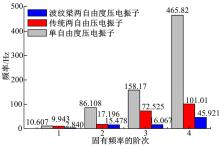
对3种结构的压电振子进行数值仿真分析, 并对比它们的固有频率值和输出电压值。首先, 在COMSOL中建立3种压电振子的仿真模型; 然后, 定义材料的属性, 具体参数如表1所示; 最后, 对模型进行网格划分并分析计算。3种压电振子谐响应分析的结果如图6所示。

表1 材料属性参数 Table 1 Parameters of material property

	Figure Option View Download New Window
	图6 3种压电振子的各阶固有频率对比图Fig.6 Resonance frequency of three piezoelectric energy harvesters

由图6可以看出, 波纹梁两自由度压电振子的固有频率最低。其中第四阶固有频率为45.92 Hz, 比传统单自由度压电振子降低419.9 Hz, 比传统两自由度压电振子降低55.1 Hz。

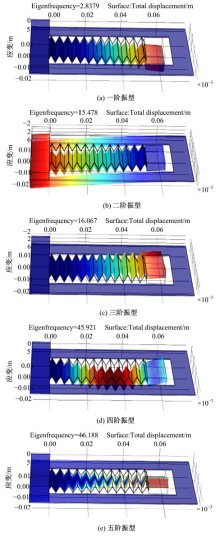
图7为波纹梁两自由度压电振子的五阶振型图。可以看出, 波纹梁压电振子的前五阶固有频率均在60 Hz以内。其中第二阶和第三阶固有频率相近, 相差0.59 Hz; 第四阶和第五阶相近, 仅相差0.27 Hz。

	Figure Option View Download New Window
	图7 波纹梁两自由度压电振子的振型图Fig.7 Modal analysis of corrugated 2-DOF PEHs

3种压电振子谐响应分析的结果表明, 波纹梁两自由度压电振子的固有频率最低, 能在0~60 Hz频段内获得五阶谐振。

图8为3种结构的压电振子末端位移随频率变化的曲线图。可以看出, 波纹梁两自由度压电振子末端位移最大, 为56 mm, 比单自由度压电振子大22 mm, 比传统两自由度压电振子大11 mm。波纹梁压电振子在0~60 Hz的频段内有3个明显的峰值, 这3个峰值对应了压电振子的五阶谐振频率。其中第一个峰值发生在一阶谐振处, 第二个峰值发生在二、三阶谐振处, 第三个峰值发生在四、五阶谐振处。

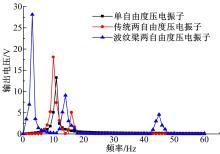
	Figure Option View Download New Window
	图8 3种压电振子末端位移随频率变化的曲线图Fig.8 Displacement curves of three PEHs versus frequency

图9为3种压电振子输出的电压值随频率变化的曲线图, 变化规律与末端位移相似。可以看出, 波纹梁压电振子在一阶谐振频率处有最大输出电压28 V, 高于单自由度压电振子15 V, 高于传统两自由度压电振子10 V。且波纹梁压电振子可以在低频段内获取多个谐振频率, 增加了能量收集的效率。

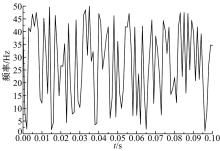
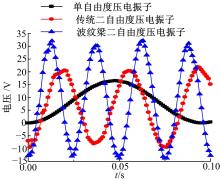
	Figure Option View Download New Window
	图9 3种压电振子的输出电压随频率变化的曲线图Fig.9 Output voltage curves of three PEHs versus frequency

为了得到3种压电振子在工作环境下的能量采集情况, 本文导入了如图10所示的随机信号来模拟工作环境下的实际振动源。图11为3种压电振子在1~50 Hz的随机振动下输出的电压值随时间的变化曲线图。可以看出, 波纹梁压电振子最大输出电压为28 V, 传统两自由度压电振子的最大输出电压为21 V, 单自由度压电振子的最大输出电压为16 V。

	Figure Option View Download New Window
	图10 随机信号的能谱图Fig.10 Energy spectrum of random signal

	Figure Option View Download New Window
	图11 3种压电振子在随机振动下输出电压随时间变化的曲线图Fig.11 Output voltage curves of three PEHs versus time

3 结束语

本文对波纹梁两自由度压电能量收集系统进行了理论和仿真分析, 并与传统单自由度和两自由度压电振子进行对比。分析结果表明, 波纹梁两自由度压电振子的固有频率最低, 一阶固有频率仅为2.8 Hz, 且能在0~60 Hz频段内获得五阶谐振。波纹梁两自由度压电振子输出的电压值最大, 为28 V。因此, 波纹梁两自由度压电振子结构可以有效降低能量收集装置的固有频率, 增加低频段谐振阶数, 优化了俘能效果, 提高了能量收集效率。后续工作将致力于设计多方向振动能量收集系统以及寻找拓宽频带的方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Anton S R, Sodano H A. A review of power harvesting using piezoelectric materials (2003-2006)[J]. Smart Material and Structures, 2007, 16(3): 1-21. [本文引用:1]
[2]	闫世伟, 杨志刚, 阚君武, 等. 压电陶瓷能量转换系统[J]. 吉林大学学报: 工学版, 2008, 38(2): 344-348. [本文引用:1]
3	Yan Shi-wei, Yang Zhi-gang, Kan Jun-wu, et al. Energy conversion system with piezoelectric ceramic[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(2): 344-348. [本文引用:1]
[3]	Elvin N G, Elvin A A. An experimentally validated electromagnetic energy harvester[J]. Journal of Sound and Vibration, 2011, 330(10): 2314-2324. [本文引用:1]
[4]	Glynne-Jones P, Tudor M J, Beeby S P, et al. An electromagnetic vibration-powered generator for intelligent sensor systems[J]. Sensors and Actuators A: Physical, 2004, 110(1-3): 344-349. [本文引用:1]
[5]	Sheu G J, Yang S M, Lee T. Development of a low frequency electrostatic comb-drive energy harvester compatible to soc design by cmos process[J]. Sensors and Actuators A: Physical, 2011, 167(1): 70-76. [本文引用:1]
[6]	Naruse Y, Matsubara N, Mabuchi K, et al. Electrostatic micropower generation from low-frequency vibration such as human motion[J]. Journal of Micromechanics and Microengineering, 2008, 19(9): 19-22. [本文引用:1]
[7]	Knight C, Joshua D, Sam B. Energy options for wireless sensor nodes[J]. Sensors, 2008, 8(12): 8037-8066. [本文引用:1]
[8]	Chen S N, Wang G J, Chien M C. Analytical modeling of piezoelectric vibration-induced micro power generator[J]. Mechatronics, 2006, 16(9): 379-387. [本文引用:1]
[9]	管青春. 悬臂梁式压电能量回收装置结构优化[D]. 合肥: 中国科学技术大学物理学院, 2011. Guan Qing-chun. Structual optimization of cantilever piezoelectric energy harvesting devices[D]. Hefei: School of Physical Sciences, University of Science and Technology of China, 2011. [本文引用:1]
[10]	Leland E S, Wright P K. Resonance tuning of piezoelectric vibration energy scavenging generators using compressive axial preload[J]. Smart Materials and Structures, 2006, 15(5): 1413-1420. [本文引用:1]
[11]	Wu Hao, Tang Li-hua, Yang Yao-wen, et al. Development of a broadband nonlinear two-degree-of-freedom piezoelectric energy harvester[J]. Journal of Intelligent Material System and Structure, 2014, 25(14): 1875-1889. [本文引用:1]

2007

0.0

... 目前,能量收集方式分为压电式^[1,2]、电磁式^[3,4]和静电式^[5,6]等,其中压电式能量收集方式因结构简单、能量密度高、环境友好、不受电磁干扰等优点而被广泛应用于振动能量收集技术 ...

2008

0.0

. 2008, 38(2):344-348

闫世伟, 杨志刚, 阚君武

College of Mechanical Science and Engineering,Jilin University,Changchun 130022,China

An energy conversion system consisting of a piezoelectric generator a circuit of storage and control was developed to convert the humanbody energy into electrical energy by means of the piezoelectric ceramic to substitute or charge automatically the battery under special conditions.The effects of the structure parameters and the supporting mode of the piezoelectric oscillator on its electrical energy generation performance were investigated experimentally.A piezoelectric generator was designed according to the experimentally optimized parameters and working mode and it was attempted to power a wireless remote controller.The measurement shows that the maximal power output of the piezoelectric generator is 58.2 mW with a 100 kΩ load.The piezoelectric generator with the circuit of storage and control system can transmit the signal to the distance of up to 10 m,satisfying the need of the wireless remote controller operation.

为实现利用压电材料收集人体能量，将其转化成电能在某些特殊应用领域替代电池或自动为电池充电的目的，设计了一个能量转换系统，该系统由压电发电装置和存储与控制电路组成。通过试验的方法研究了压电振子在结构参数、支撑方式等多种因素影响下的发电特性，根据试验取得的优化参数和工作方案设计了压电发电装置，并尝试利用其为无线遥控器供电。经过试验测试，压电发电装置在外接100 kΩ负载时最大输出功率为58.2 mW,连接存储与控制电路时可满足无线遥控器（以开关无线遥控器为例）的使用要求,信号传输距离达到10 m以上。

2008

0.0

2011

0.0

2004

0.0

2011

0.0

2008

0.0

2008

0.0

... 车辆驶过的路面、工作中的机器、运动的人体等都是环境中常见的振动源^[7],它们振动频率约为0~250 Hz^[8],属于低频振动 ...

2006

0.0

... 车辆驶过的路面、工作中的机器、运动的人体等都是环境中常见的振动源^[7],它们振动频率约为0~250 Hz^[8],属于低频振动 ...

2011

0.0

. 2011, :- DOI:doi:10.7666/d.d141975

Structual optimization of cantilever piezoelectric energy harvesting devices

悬臂梁式压电能量回收装置结构优化[D]

Guan Qing-chun.

管青春

随着低功率无线传感网络以及便携式电子设备的应用越来越广泛，电池供能凸显出诸多缺点，如寿命和能量密度有限、更换维护麻烦、污染环境等，因此回收环境能量来实现微电子设备的自主供能，有巨大的应用前景和重要的研究意义。环境中普遍存在振动，回收振动能量可采用电磁式、静电式或者压电式方法，其中，压电能量回收因结构简单、适用性广、不需额外电源而成为研究的热点。压电能量回收的两种回收模式是3-1模式和3-3模式。压电能量回收优化包括回收电路优化和回收结构优化，其中回收结构优化途径有频率匹配、改善应变分布以及提高机电耦合系数等。基于3-1模式...

... 如管青春^[9]提出一种H形质量块压电回收结构,提高了压电片的利用率和能量收集效率 ...

2006

0.0

... Leland等^[10]通过施加轴向预应力来改变装置的固有频率 ...

2014

0.0

... Wu等^[11]设计了一种断路器式两自由度压电收集结构,有效拓宽了工作频带 ...