月球次表层回转取样钻头构型设计

引用本文

赵德明, 姜生元, 唐德威, 侯绪研, 邓宗全. 月球次表层回转取样钻头构型设计. 2017, 47(4): 1149-1158
ZHAO De-ming, JIANG Sheng-yuan, TANG De-wei, HOU Xu-yan, DENG Zong-quan. Structure design of lunar subsurface sampling drill. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1149-1158 复制到剪切板

Permissions

月球次表层回转取样钻头构型设计

赵德明, 姜生元, 唐德威, 侯绪研, 邓宗全

哈尔滨工业大学宇航空间机构及控制研究中心,哈尔滨 150001

通讯作者：唐德威(1966-),男,教授,博士生导师.研究方向:机械设计,宇航空间机构.E-mail:dwtang@hit.edu.cn

作者简介:赵德明(1986-),男,博士研究生.研究方向:机械设计,宇航空间机构.E-mail:miancer@163.com

基金:中国探月工程预研项目(TY3Q20110001,TY3Q20110005); 国家自然科学基金项目(51105092,61403106); 国家国际科技合作专项项目(2014DFR50250).

摘要

以月球次表层钻进取样工程为应用背景,从功能组成角度定义了月球取样钻头的子结构,将排屑通道优化设计作为钻头构型改进重点。采用曲面基体和空间螺旋曲线包络方式设计排屑通道,并对排屑通道进行了微分几何建模,设计了一种新型曲面构型钻头。通过多种典型构型钻头在模拟月壤条件下的负载对比实验对该构型进行了测试,结果表明该新型钻头的负载约为其他构型钻头的30%~45%。最后,还从细观角度应用离散单元仿真方法验证了曲面螺旋翼钻头具有优良的大颗粒适应性。

关键词: 机械设计; 月表取样; 钻头构型设计; 排屑通道建模

中图分类号:TH122,V476.3 文献标志码:A 文章编号:1671-5497(2017)04-1149-10

Structure design of lunar subsurface sampling drill

ZHAO De-ming, JIANG Sheng-yuan, TANG De-wei, HOU Xu-yan, DENG Zong-quan

Research Center of Aerospace Mechanism and Control, Harbin Institute of Technology, Harbin 150001,China

Abstract

The sub-structures of drill bit are defined based on the function, and the optimization of the chip removing structure is taken as the key of shape-configuring design of the drill bit. A new drill shape-configuring design with spherical base and spiral blade is proposed. Experimental results show that the pay load of drill bit with the new chip removing structure is only 30% ~ 40% of the other typical drill bit forms. The gravels removing mechanism is studied using Discrete Element Method (DEM), and the results show that the new drill bit structure is more adaptable.

Keyword: mechanical design; lunar soil sampling; auger drill design; chip removing structure

Show Figures

0 引言

目前在航天工程领域, 月表刺入取样普遍采用钻取或冲击钻取方式^[1]。世界范围内已取得成功的月球取样返回活动包括美国的Apollo15、16、17以及前苏联的Luna16、20、24系列^[2]。这些探测活动中, 最大钻取深度为3 m^[3]。此外在其他地外天体次表层探测活动中, 美国的好奇号、勇气号火星探测器、罗塞塔彗星探测器等都采用了钻进取样方法^{[4, 5]}。除钻取方式外, 还有火星探测器小猎犬二号采用了锤击贯入方式, 欧洲空间局在研的仿生木蜂方式, 但以上两种方式只能实现松软对象的浅层刺入^{[6, 7]}。在现阶段, 回转及回转冲击钻进方法在刺入效率、对象适应性、取样能力方面有着不可替代的优势。

从现有的月球探测图像及地质研究资料^[8]分析, 除少数大落差月崖局部有基岩裸露外, 月球表面主要由月壤风化物覆盖, 已知覆盖深度约10~15 m, 远大于现有探测深度3 m。月表风化层的主要构成物包络直径小于1 mm, 中径在70 μ m左右, 大直径颗粒较少。本文从月表风化层与取样钻具之间比例关系将作用对象分为月壤、临界尺度月壤颗粒和月岩3类。其中月壤是钻进取样的主要对象, 通常其刺入难度较月岩低。但由于月壤颗粒形态及其形成环境条件特殊, 在距月表60 cm以下区域月壤密实度会达到90%以上, 这导致月壤的流动性较差^[9]。临界尺度颗粒是指直径与钻头尺寸相近的月壤颗粒, 在月表风化层中临界尺度颗粒数量较少, 但对钻头的排屑性能影响明显, 会导致钻进负载波动, 严重时导致卡钻或者钻具结构损坏^[10]。

在地表地质钻探取样领域, 广泛采用液态水作为排屑及冷却介质, 地质钻头构型设计主要考虑回转钻进的稳定性及排屑液导流性能^[11]。为实现取样任务, 月表次表层取样钻具应当在有限时间和能量供给条件下具备以下几个方面的能力^[12]:①不依赖排屑介质并保证顺畅排屑; ②对临界尺度颗粒具有强适应性; ③无冷却介质条件下, 具备一定的岩石刺入能力; ④保证取样率及保持样品原态信息能力。

现有月球取样钻具基体以平面、浅锥及阶梯构型为主, 排屑翼构型一般由切削刃分布决定, 以直线构型为主。比较有代表性的有Apollo系列的平面基体直线切削刃构型和Luna系列的阶梯基体线性排列柱状切削刃构型^[13]。此外在在研的火星探测钻具设计中, 也大多具有相似特征, 例如欧洲空间局的Exomars系列采用浅锥基体直线排屑翼结构, NASA(美国国家航空和宇宙航行局)和JPL(美国喷气推进实验室)合作研发的MSR系列钻具采用的平面基体直线排屑结构^{[14, 15]}。以上多个系列的近地天体取样钻具大多是以岩石破碎为首要目标进行设计的, 当钻进对象为月壤及临界尺度颗粒混合物时, 存在钻进效率低下且容易发生卡钻的问题^[16]。

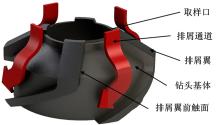
按功能结构分类, 月表取样钻具的设计元素可以分成排屑通道、取样口结构以及岩石破碎结构3个部分。其中排屑通道的设计主要影响钻具对月壤的排屑能力, 以及临界尺度颗粒的通过性。本文着重对钻具排屑构型进行设计分析, 即钻具基体和排屑翼构型。在以上所列4种能力中, 与钻头排屑构型设计直接相关的是前两种能力, 本文着重对钻头的排屑能力和临界尺度颗粒适应性进行系统研究。

1 排屑通道设计

1.1 钻进对象

钻头在目标月壤钻进区域实现钻进的过程包含两个步骤:首先破坏原位月壤/月岩的内部结合能, 使其形成碎屑; 之后通过钻具的排屑机制将碎屑运移出钻进区。在钻进过程中发生排屑不畅会导致回转转矩升高, 进给失效。在地面地质钻进中通常采用水或者空气作为排屑的辅助介质, 兼具冷却散热的作用。

由于受月球环境限制, 月球次表层取样钻具的排屑过程难以引入介质辅助。月壤或月岩碎屑只能通过钻头排屑通道和包络原位月壤的差动及挤压作用排出钻头作用区域。因此钻头的排屑通道包络设计决定了这一排屑过程的能效, 优化设计钻头的排屑通道构型是提升钻头性能的一个重要途径。

月壤中包含的尺寸与钻头尺寸相接近的岩块, 是钻头排屑的难点之一。该类岩块受自身尺度限制, 其周围原位月壤为其提供的固持力不足以保证钻头对其实现稳定切削, 在钻具钻进过程中容易发生随动。如果钻头的排屑通道设计无法疏导此类岩块, 钻具负载将产生波动冲击, 严重时可能破坏钻具机械结构, 甚至引发卡钻。本文中定义此类尺度的岩块为临界尺度月壤颗粒, 其尺度区间约为 $\begin{matrix} h < d_{p} < 0.5 D_{drill}, \end{matrix}$ 其中 $\begin{matrix} h \end{matrix}$ 为钻头排屑翼的高度, $\begin{matrix} D_{drill} \end{matrix}$ 为钻头外径。在月球次表层钻进取样活动中, 钻头遭遇此类临界尺度岩块的概率远大于分布稀疏的月岩。

1.2 排屑通道定义与组成

在本文中, 定义钻头的排屑通道由钻头基本几何体与翼状凸起共同包围构成, 图1为一种典型的浅锥基体直线排屑翼排屑通道构型。

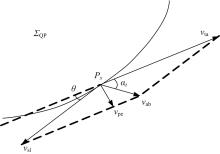
	Figure Option View Download New Window
	图1 钻头排屑构型基本要素示意图Fig.1 Diagram of drill bit basic elements

伴随钻头回转钻进, 钻头排屑翼前接触面推动排屑通道内月壤与包围原位月壤产生滑移, 从而实现排屑。图2为月壤在排屑通道内受力状态与排屑翼角度关系。

	Figure Option View Download New Window
	图2 钻头排屑区月壤受力分析示意图Fig.2 Diagram of force analysis of chip flow

图2中月壤碎屑受力的基本平衡关系可由下式表示:

$\begin{matrix} cosθF + sinθN = \cos α_{t} F_{ss} (1) \end{matrix}$

式中: $\begin{matrix} α_{t} \end{matrix}$ 为钻头的排屑角, 该角定义为实际排屑方向与钻头回转线速度方向的夹角; $\begin{matrix} θ \end{matrix}$ 为钻头排屑翼倾角, 该角定义为排屑翼所在直线与钻头回转线速度方向的夹角, 当排屑翼为曲线时, 其定义为排屑翼曲线在该处的切线方向与钻头回转线速度方向的夹角; N为螺旋翼上的正压力; F为螺旋翼对月壤碎屑的摩擦力; F_ss为月壤碎屑受钻头前端原位月壤作用的摩擦力。

通过图2中 $\begin{matrix} AB' \end{matrix}$ 排屑翼对应的对比受力分析及式(1)可以看到, 当排屑翼与钻头径向成一定角度时, 月壤受向外侧滑移力, 角度越大, 滑移分力越大。对于直线排屑翼构型, 月壤排屑翼与钻具径向之间角度随排屑位置距离钻头回转轴线距离发生变化。图2中角 $\begin{matrix} θ ‴ < θ ″, \end{matrix}$ 角度变化会导致钻具排屑通道不同区域排屑能力存在差异。

	Figure Option View Download New Window
	图3 典型钻头基体剖面结构示意图Fig.3 Diagram of cross section of drill bit base

图3为几种典型的钻头基体剖面结构示意图。由于月壤流动性较差, 排屑通道中的转折结构对排屑有较强的阻碍作用, 因此钻具基体构型采用曲面结构可以使排屑通道空间构型更加平滑。

2 排屑通道几何建模及排屑能力

计算

2.1 钻头排屑翼曲线建模

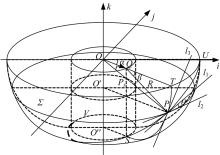
钻头作为钻具执行末端, 同时也是排屑的初始端, 其最优排屑通道构型即是与钻杆排屑螺旋实现共体设计, 即钻头排屑翼与钻杆螺旋翼共享几何参数, 同时钻头基体与钻杆基体平滑过渡, 从而实现月壤对象的低阻力排屑。为实现以上的设计设想, 钻头基体采用圆弧过渡, 钻头螺旋翼设计为依附于圆弧曲面上的空间螺旋线。圆弧过渡的优点在于可以实现小曲率与小尺寸之间的平衡。图4为钻头基体示意图, 图中曲线P_s为排屑翼曲线。图4中所示曲面 $\begin{matrix} Σ \end{matrix}$ 方程为:

$\begin{matrix} Σ = \{\begin{matrix} (r + Rcosβ) cosα, \\ (r + Rcosβ) sinα, \\ Rsinβ \end{matrix}\}, (\begin{matrix} α \in [0, 2 π], \\ β \in [- \frac{π}{2}, 0] \end{matrix}) (2) \end{matrix}$

定义螺旋翼的回转方向与螺旋翼前接触面在任意点处的切平面之间的角度为钻头螺旋升角, 取该角度值为定值, 且θ ∈ [π /18, π /6], 则该几何定义可以用参数微分方程表达:

$\begin{matrix} Rdβ = tanθ (r + Rcosβ) dα (3) \end{matrix}$

	Figure Option View Download New Window
	图4 空间螺旋曲线几何模型图Fig.4 Geometric model of spiral curve

方程求解, 把式(3)代入到式(2)中, 对方程进行积分, 当 $\begin{matrix} R \geq r \end{matrix}$ 时, 有:

$α = \frac{Ra}{tanθ (R + r)} \ln |\frac{\tan \frac{β}{2} + a}{\tan \frac{β}{2} - a}| + C (4)$

其中

$a = \sqrt[]{\frac{R + r}{R - r}} (5)$

当 $\begin{matrix} R = r \end{matrix}$ 时, 有:

$\begin{matrix} α = \frac{\tan \frac{β}{2}}{tanθ} + C (6) \end{matrix}$

当 $\begin{matrix} R \leq r \end{matrix}$ 时, 有:

$α = \frac{2 Rb}{tanθ (R + r)} \arctan (\frac{1}{b} \tan \frac{β}{2}) + C (7)$

其中

$b = \sqrt[]{\frac{r + R}{r - R}} (8)$

则可以得到曲线方程:

$\begin{matrix} P_{s} = \{\begin{matrix} (r + Rcosβ) \cos (\frac{R \sqrt[]{\frac{R + r}{R - r}}}{tanθ (R + r)} \ln |\frac{\tan \frac{β}{2} + \sqrt[]{\frac{R + r}{R - r}}}{\tan \frac{β}{2} - \sqrt[]{\frac{R + r}{R - r}}}|) i + \\ (r + Rcosβ) \sin (\frac{R \sqrt[]{\frac{R + r}{R - r}}}{tanθ (R + r)} \ln |\frac{\tan \frac{β}{2} + \sqrt[]{\frac{R + r}{R - r}}}{\tan \frac{β}{2} - \sqrt[]{\frac{R + r}{R - r}}}|) j + Rsinβk, R \geq r \\ (r + Rcosβ) \cos (\frac{\tan \frac{β}{2}}{tanθ}) i + (r + Rcosβ) \sin (\frac{\tan \frac{β}{2}}{tanθ}) j + Rsinβk, R = r \\ (r + Rcosβ) \cos (\frac{2 R \sqrt[]{\frac{r + R}{r - R}}}{tanθ (R + r)} \arctan (\sqrt[]{\frac{r - R}{r + R}} \tan \frac{β}{2})) i + \\ (r + Rcosβ) \sin (\frac{2 R \sqrt[]{\frac{r + R}{r - R}}}{tanθ (R + r)} \arctan (\sqrt[]{\frac{r - R}{r + R}} \tan \frac{β}{2})) j + Rsinβk, R \leq r \end{matrix} (9) \end{matrix}$

式中: $\begin{matrix} β \in [- \frac{π}{2}, 0] 。 \end{matrix}$

当方程参数(R=8 mm, r=7.5 mm, θ =π /12)时, 图5为Matlab软件绘制的空间曲线图。钻头螺旋翼的设计重点是其与月壤直接作用实现排屑的前触面, 该面的设计是一个以 $\begin{matrix} P_{s} \end{matrix}$ 曲线为母线与基体曲面处处垂直的空间可展曲面。在由该曲面和基体确定的排屑通道内, 月壤碎屑的排屑差动受力状态与钻杆排屑槽内相同, 同时方便加工。

	Figure Option View Download New Window
	图5 钻头排屑通道曲线Fig.5 Curve of chip removing structure

图6为基于 $\begin{matrix} P_{s} \end{matrix}$ 曲线设计的双通道曲面螺旋钻头三维模型图。

	Figure Option View Download New Window
	图6 钻头构型三维效果图Fig.6 3D model of drill bit

2.2 钻头排屑能力计算

在以该螺旋曲线为基础的排屑通道设计中, 对钻头的排屑能力进行建模计算。图7为排屑通道中月壤碎屑排屑流动的速度分解示意。图7中, $\begin{matrix} v_{ta} \end{matrix}$ 为钻头回转线速度; $\begin{matrix} v_{pe} \end{matrix}$ 为排屑流动中的有效速度部分, 该速度方向为图4中曲线 $\begin{matrix} ST \end{matrix}$ 的切线方向; $\begin{matrix} v_{ab} \end{matrix}$ 为以地面静止坐标系为参考系的月壤碎屑排屑流动绝对速度; $\begin{matrix} v_{sl} \end{matrix}$ 为排屑流动相对钻头螺旋翼前接触面的滑移速度。

	Figure Option View Download New Window
	图7 钻头排屑通道中排屑流动速度分解示意图Fig.7 Velocity resolution of chip flow

对于钻头区域, 不同位置的排屑需求可以表达为:

$\begin{matrix} Φ_{re} = V^{*} π [{(Rcosβ + dcosβ + r)}^{2} - r^{2} K_{sample}] (10) \end{matrix}$

式中: $\begin{matrix} d \end{matrix}$ 为螺旋翼高度; $\begin{matrix} K_{sample} \end{matrix}$ 为钻头的均值取样率; $\begin{matrix} V^{*} \end{matrix}$ 为钻头的理论极限进给速率。

钻头在不同位置上的排屑能力可以表达为:

$\begin{matrix} Φ = 2 πKdω {[(R + d) cosβ + r]}^{2} Γ (11) \end{matrix}$

式中: $\begin{matrix} ω \end{matrix}$ 为钻具的回转速率; $\begin{matrix} K \end{matrix}$ 为修正系数, 该系数包含因为钻头进给速度、月壤碎屑排屑速率分布不均等因数产生的计算误差的修正^[18]; $\begin{matrix} Γ \end{matrix}$ 为钻头的排屑能力系数, 其物理定义为v_pe/v_ta, 该系数与钻头的螺旋角有关, 又联立式(10)(11)有:

$\begin{matrix} V^{*} = \frac{2 Kdω {[(R + d) cosβ + r]}^{2} Γ}{{(Rcosβ + r + dcosβ)}^{2} - r^{2} K_{sample}} (12) \end{matrix}$

式中:关键参数 $\begin{matrix} Γ \end{matrix}$ 可由图7所示的速度分析得到:

$\begin{matrix} Γ = \frac{v_{pe}}{v_{ta}} = \frac{tanθtan α_{t}}{tanθ + \tan α_{t}} (13) \end{matrix}$

式中: $\begin{matrix} α_{t} \end{matrix}$ 为月壤碎屑排屑角, 该角度定义为月壤碎屑流动方向与钻头回转线速度方向间的夹角^[17]。设 $\begin{matrix} σ_{*} \end{matrix}$ 为钻头排屑槽内土体围压, 式(1)可以改写为:

$\begin{matrix} \begin{matrix} \tan φ_{s} \cos (α_{t} + θ) (h_{0} σ_{*} + h_{0} dρ g_{e} sinβ) = \\ \tan φ_{m} (h_{0} σ_{*} - h_{0} dρ g_{e} sinβ) + 2 \tan φ_{m} d σ_{*} + \\ h_{0} dρ g_{e} sinθcosβ (14) \end{matrix} \end{matrix}$

式中: $\begin{matrix} \tan φ_{s} \end{matrix}$ 为排屑区月壤碎屑与包围原位月壤间的当量摩擦因数; $\begin{matrix} \tan φ_{m} \end{matrix}$ 为排屑区月壤碎屑与钻头基体间的当量摩擦因数; $\begin{matrix} h_{0} \end{matrix}$ 为排屑槽宽度基值; $\begin{matrix} g_{e} \end{matrix}$ 为重力加速度, 这里的角标e是为了强调在计算中为了与实验相对应采用了地面加速度, 而不是月面加速度。

将式(12)(13)(14)联立, 可以得到关于 $\begin{matrix} Γ \end{matrix}$ 的隐式方程, 设 $\begin{matrix} θ \end{matrix}$ 为π /12, 且定义:

$\begin{matrix} E_{t} = \frac{\tan φ_{m}}{\tan φ_{s}} (15) \end{matrix}$

为排屑环境系数, 该数值可以通过月壤的摩擦实验测试获取, 对于本文中所使用的HIT-LS1模拟月壤, 其测定值为0.49~0.54, 取 $\begin{matrix} E_{t} = 0.52, 对 Γ \end{matrix}$ 进行求解, 可得 $\begin{matrix} Γ \end{matrix}$ 在钻头排屑区不同位置的分布, 如图8所示。

	Figure Option View Download New Window
	图8 Γ 在钻头排屑区不同位置的数值分布Fig.8 Distribution of Γ on drill

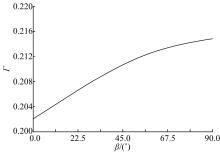
由以上建模计算可知, 该螺旋构型钻头靠近取样口区域的计算排屑能力系数要略大于其与钻杆连接区域。由于钻头与钻杆一体化设计, 连接区排屑能力即为钻杆的排屑能力。钻头的排屑能力系数极值约高于钻杆7%, 这种差异是由重力与排屑方向的夹角变化产生的。当 $\begin{matrix} θ \end{matrix}$ 取值变化时, 该趋势变化很小。

鉴于在钻头区域排屑流动存在的平衡关系, 钻头前端的排屑需求远低于钻杆区, 因此在具体设计中, 钻头顶端螺旋翼可以进行加厚, 通过缩小排屑通道与钻杆排屑相协调, 并以此进行取样结构和岩石钻进结构设计。

以上关于月壤排屑的建模计算属于准静力学范畴, 在计算中关注月壤碎屑的整体运动, 忽略了月壤作为颗粒材料的本构性质对其一体流动的影响。在仿真实验观察中月壤本构对其流动速度分布影响有限, 且相关建模复杂, 在当前的计算中并未详细讨论。

另外, 为验证曲面螺旋构型钻具设计在月壤钻取中的优势, 进行了两个系列的实验和仿真。第一部分实验对象为均质月壤, 测试了多种构型钻头在大进给条件下的负载特性。第二部分实验将实验对象扩展到临界尺度混合模拟月壤对象。在实验中采用了放大尺度钻具来提高负载辨识性。第二部分实验辅以离散元仿真, 从细观角度分析钻具构型对其排屑能力的影响机理。

3 排屑通道构型的对比实验及仿真

3.1 实验简介

钻头的排屑能力直接影响钻具负载, 此外, 降低钻具负载也是钻具设计优化的显性目标。因此, 本文选取钻具负载作为实验评价指标。

本文中钻头负载是指在一定的进给参数及钻进对象条件下钻头的钻压力及回转扭矩。钻具在进行月壤物质钻进时, 其钻进扭矩主要由以下3部分组成:①钻头机械结构与月壤的摩擦力; ②钻头区月壤碎屑堆积压导致的其与原位月壤间摩擦力; ③钻头切削刃或磨削刃破碎原位月壤结合能时做功扭矩, 这部分负载在月壤钻进中处于可以忽略的次要部分, 但在岩石钻进中占主要部分。钻头的进给力主要由以下两个部分组成:①钻头排屑区月壤堆积压产生的支反力; ②钻头切削刃或磨削刃压入原位月壤时所需的压力, 这部分进给力在岩石钻进中占主要部分。

在月壤钻削过程中, 如果发生钻头前端排屑不畅的情况, 钻头的扭矩和钻压力会随月壤碎屑内压升高而迅速上升, 甚至发生堵钻现象。这也是钻头排屑通道构型优化设计所要避免的状态。在月壤钻进中为破坏原位月壤结合能所产生的负载比重很小。

本实验的目标即是测试钻具构型变化对其负载的影响, 进而间接评价不同钻具排屑通道构型的排屑能力。为了提高构型因素对钻具负载影响的分辨率, 在钻具构型验证实验中引入了放大尺度钻具, 相比于工程中钻具尺寸, 钻具放大率为8/3。在实验对象为月壤类物质时, 钻具负载中切削项占比很小。

对于负载中的积屑项, 该负载主要由摩擦产生, 负载大小与接触截面面积成正比, 当钻具尺寸放大率为8/3时, 负载放大率为尺寸放大率的平方约为7/1。这个估计数值与实验结果相吻合。放大钻具钻进规程为(60 r/min, 80 mm/min)、常尺寸钻具钻进规程为(100 r/min, 100 mm/min)时, 两者的均值扭矩分别为5~8、1~1.5 N· m, 均值钻压力分别为60~90、10~20 N。

多构型放大钻头负载比对实验介质为采用震动压实方法制备的模拟月壤, 该模拟月壤相对密实度为97%。这与距离月球表面600 mm以下的原位月壤密实度相接近。图9为实验用模拟月壤及进行钻头测试的实验平台。

	Figure Option View Download New Window
	图9 模拟月壤钻进平台、实验钻具及月壤桶Fig.9 Drilling platform, drill stem, and lunar soil simulant bucket

3.2 均质月壤钻进实验

多构型钻头负载比对实验中设计三系列钻头构型, 分别测试了排屑翼角度及基体形状对其排屑能力的影响。表2为钻头编号与钻头构型的对应关系。

表2 钻头编号 Table 2 Serial number of drill bit

在第1系列实验中, 采用了平面基体构型的一系列放大钻具, 各钻具排屑翼与径向方向夹角分别为0° 、30° 、60° 、90° , 另外还引入了一组平面螺旋排屑翼钻具进行比对, 如图10所示。

	Figure Option View Download New Window
	图10 平面构型钻头系列Fig.10 Series of flat base drill

在第2系列实验中, 采用了不同基体结构的直排屑翼构型钻具, 基体形状包含平面结构, 锥面结构, 阶梯结构和球环结构。由于钻头构型是一个复杂参数系统, 这里的构型比对实验以定性研究为主。在具有代表性的结构参数下, 测试钻头基体形状对其排屑负载影响的一般规律。图11为实验中引入的几种钻头。

	Figure Option View Download New Window
	图11 变基体构型直排屑翼钻头系列Fig.11 Series of various base drill with straight wings

	Figure Option View Download New Window
	图12 变基体构型螺旋排屑翼钻头系列Fig.12 Series of various base drill with spiral wings

在第3系列实验中, 对前两组实验构型进行了整合。采用的钻具构型为螺旋翼附加不同基体的构型组合, 如图12所示。

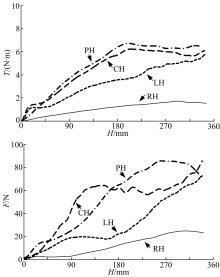
	Figure Option View Download New Window
	图13 平面构型钻头系列实验负载曲线Fig.13 Load curve of plat base drills

3个系列钻进实验统一采用回转速率60 r/min、进给速率100 mm/min的钻进规程。在第1系列实验中, 钻具负载情况如图13所示, 可以看到钻头负载总体上随排屑翼角度的增加而逐渐降低。当螺旋翼采用平面螺旋结构时其负载有明显降低。为对比方便, 图13中还额外增加了RH构型钻头的负载曲线。

当排屑结构为螺旋形时其负载对比图见图14, 负载表现为曲面直翼钻头≈ 锥形直翼钻头< 阶梯螺旋翼≈ 平面螺旋翼钻头。当排屑结构为螺旋形时其负载对比图如图15所示, 负载表现为曲面螺旋翼钻头< 阶梯螺旋翼< 锥形螺旋翼钻头≈ 平面螺旋翼钻头。并且负载低于平面排屑结构, 曲面螺旋结构在负载降低上优势明显。

	Figure Option View Download New Window
	图14 变基体构型直排屑翼钻头系列实验负载曲线Fig.14 Load curve of various base drill with straight wings

	Figure Option View Download New Window
	图15 变基体构型螺旋排屑翼钻头系列实验负载曲线Fig.15 Load curve of various base drill with spiral wings

从以上几组实验结果可以看到, 曲面螺旋钻具平均负载分别约为其他构型钻具的30%~45%。

3.3 临界尺度模拟月壤钻进实验

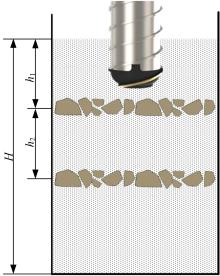
在进一步的实验中, 测试验证了在均质月壤负载测试中表现较优的几种钻具构型。含临界尺度颗粒模拟月壤中的负载实验如图16所示。图中H=360 mm为月壤桶月壤填深, h₁=h₂=130 mm处为临界颗粒层, 颗粒层厚度约为30 mm。实验通过记录分析钻头在通过临界颗粒层时的负载特性来评价不同钻头排屑通道构型对钻头临界尺度颗粒适应性的影响。这里提出的负载特性主要包含两个方面, 一方面是钻具负载峰值; 另一方面是钻具在通过颗粒层之后的卸载速度。

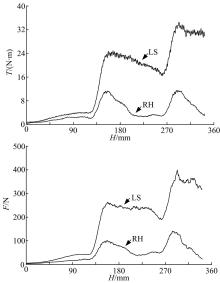
	Figure Option View Download New Window
	图16 含临界尺度颗粒层模拟月壤制备示意图Fig.16 Diagram of lunar soil simulant with critical size gravels

图17为阶梯直刃构型(LS)钻头与曲面螺旋构型(RH)钻头在含颗粒层模拟月壤中的钻进负载。从图17可以看到两者负载区别明显, LS构型钻头峰值负载更高, 而且无法实现有效卸载, 在面对较厚的颗粒层时容易发生过载, 导致钻具卡死。RH构型钻头的峰值负载控制在LS构型钻头的1/3~1/2之间, 同时通过颗粒层后可以实现有效卸载, 顺利通过颗粒层, 不会产生明显的负载积累。

	Figure Option View Download New Window
	图17 RH及LS两种构型钻头在突破临界尺度颗粒层时的负载曲线Fig.17 Load curve of RH and LS drill bit penetrating gravel layers

	Figure Option View Download New Window
	图18 含临界尺度颗粒的离散元数值模拟月壤建模Fig.18 DEM Model of lunar soil simulant with critical size gravels

3.4 临界尺度模拟月壤钻进仿真

本文应用离散元仿真方法对大颗粒在钻具排屑结构中的流动进行了模拟。使用的离散元仿真软件为EDEM(版本号为2.5), 颗粒间基本作用模型为Hertz-Mindlin模型, 仿真月壤的中径为1 mm, 仿真中颗粒弹性模量为10⁸Pa, 颗粒间摩擦因数为0.8, 颗粒及钻具间摩擦因数为0.3。

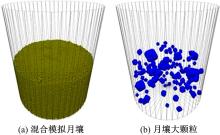
图18(a)为通过离散元方法生成的混合模拟月壤, 图18(b)为混合模拟月壤中包含的月壤大颗粒。仿真中所采用的两种钻头分别是曲面螺旋构型(RH)钻头和前苏联Luna24钻具采用的相似构型钻头, 该钻头是一种典型的阶梯直刃构型(LS)钻头。

图19为临界尺度颗粒在钻头排屑槽内的流线及流速分布状态。

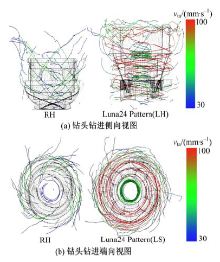	Figure Option View Download New Window
	图19 RH及LS两种构型钻头钻进时临界尺度颗粒流线图Fig.19 Flow line chart of critical size gravels around RH and LS drill bit

图19中流线高速部分颗粒流速在100 mm/s附近, 该速度与钻头平均回转线速度相接近。从图19可以看到, 临界尺度颗粒在RH构型钻头中的排屑曲线更加规律, 与图19中所示的理论排屑方向相一致, 同时颗粒并没有同钻头发生明显地随动, 这表现为颗粒流速控制在40~50 mm/s以内。而LH构型钻具的颗粒排屑流线则显得杂乱, 颗粒流速快, 大量颗粒同钻头共体回转, 并没有实现有效排屑。

4 结论

(1)在钻取月壤对象时钻头的排屑通道构型设计是钻头设计的关键, 作者应用空间几何建模方法设计了一种新型曲面螺旋构型钻头。通过螺旋排屑模型, 计算了该钻头的理论排屑能力, 计算结果表明, 曲面螺旋构型钻头的排屑能力优于其他几种典型钻头构型的排屑能力。

(2)对模拟月壤的钻进实验结果表明, 在相同钻进规程条件下, 曲面螺旋构型钻头负载明显低于平面基体、锥形基体、阶梯基体等构型钻头, 其中曲面螺旋构型钻头回转扭矩约为平面钻头和锥形基体钻头的30%, 约为阶梯基体钻头的50%。实验结果还表明, 在平面基体构型钻头中, 排屑翼构型对钻进负载有一定影响, 表现为翼倾角越大, 负载越低。同时, 在基体构型影响实验结果表明, 球形基体和阶梯基体构型钻头的负载表现优于锥形基体和平面基体钻头。

(3)测试了曲面螺旋构型钻头在临界尺度月壤中的负载表现, 并用阶梯直刃构型钻头做了对比实验。曲面螺旋钻头在通过临界尺度颗粒层的峰值负载为阶梯构型钻头的1/3~1/2, 且曲面螺旋钻头在通过颗粒层之后的卸载效率优于阶梯基体钻头, 不会产生负载积累。

(4)为了从细观角度解释以上负载差别, 应用离散元方法建立了临界尺度月壤混合模型, 并对曲面螺旋构型和阶梯直刃构型钻头的临界尺度颗粒排屑过程进行了仿真。仿真结果显示临界尺度颗粒在曲面螺旋构型钻头排屑结构中流动与预期排屑方向一致, 没有产生卡滞和随动, 而阶梯直刃钻头出现大颗粒随动现象。仿真结果进一步证实所设计的曲面螺旋钻头具有优良的颗粒尺寸适应性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zacny K, Bar-Cohen Y. Drilling in Extreme Environments: Penetration and Sampling on Earth and other Planets[M]. London: Wiley, 2008. [本文引用:1]
[2]	Zheng Y, Ouyang Z, Li C, et al. China's Lunar exploration program: present and future[J]. Planetary and Space Science, 2008, 56: 881-886. [本文引用:1]
[3]	Anttila M. Concept evaluation of mars drilling and sampling instrument[D]. Helsinki: Helsinki University of Technology, 2005. [本文引用:1]
[4]	Duffard R, Kumar K. A multiple-rendezvous, sample-return mission to two near-earth asteroids[J]. Advances in Space Research, 2011, 48: 120-132. [本文引用:1]
[5]	Ulamec S, Biele J, Fantinati C, et al. Rosetta land er after seven years of cruise, prepared for hibernation[J]. Acta Astronautica, 2012, 84: 151-159. [本文引用:1]
[6]	Richter L, Coste P. Development and testing of subsurface sampling devices for the beagle 2 land er[J]. Planetary and Space Science, 2012, 50: 903-913. [本文引用:1]
[7]	Pitcher C, Gao Y. Analysis of drill head designs for dual-reciprocating drilling technique in planetary regoliths[J]. Advance in Space Research, 2015, 56(8): 1765-1776. [本文引用:1]
[8]	Carrier W, Olhoeft G R, Mendell W. Lunar Sourcebook: A User's Guide to the Moon[M]. Cambridge: Cambridge University Press, 1991: 475-594. [本文引用:1]
[9]	Fu X, Huck D. Effect of particle shape and size on ow properties of lactose powders[J]. Particuology, 2012, 10: 203-208. [本文引用:1]
[10]	Mckay D S, Fruland R M. Grain size and the evolution of lunar soils[C]//Proceedings of the Fifth Lunar Conference, Houston, Texas, 1974: 887-906. [本文引用:1]
[11]	李大佛. 金刚石、PDC钻头与工艺学[M]. 北京: 北京地质出版社, 2008. [本文引用:1]
[12]	欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005. [本文引用:1]
[13]	Zacny K, Bar-Cohen Y. Drilling systems for extraterrestrial subsurface exploration[J]. Astrobiology, 2008, 8(3): 665-706. [本文引用:1]
[14]	Magnani P G, Re E, Ylikorpi T, et al. Deep drill (DeeDri) for Mars application[J]. Planetary and Space Science, 2004, 52: 79-82. [本文引用:1]
[15]	Magnani E, Izzo P, Rizzi M. 2 ExoMars multi rod drill development and testing[C]//The 10th Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk, Netherland s, 2008. [本文引用:1]
[16]	Tian Y, Tang D, Deng Z, et al. Drilling power consumption and soil conveying volume performance of lunar sampling auger[J]. Chinese Journal of Mechanical Engineering, 2015, 28: 451-459. [本文引用:1]
[17]	Zhao D, Tang D, Hou X, et al. Soil chip convey of lunar subsurface auger drill[J]. Advance in Space Research, 2016, 57(10): 2196-2203. [本文引用:1]

2008

0.0

... 0 引言目前在航天工程领域,月表刺入取样普遍采用钻取或冲击钻取方式^[1] ...

2008

0.0

... 世界范围内已取得成功的月球取样返回活动包括美国的Apollo15、16、17以及前苏联的Luna16、20、24系列^[2] ...

2005

0.0

... 这些探测活动中,最大钻取深度为3 m^[3] ...

2011

0.0

... 此外在其他地外天体次表层探测活动中,美国的好奇号、勇气号火星探测器、罗塞塔彗星探测器等都采用了钻进取样方法^[4,5] ...

2012

0.0

... 此外在其他地外天体次表层探测活动中,美国的好奇号、勇气号火星探测器、罗塞塔彗星探测器等都采用了钻进取样方法^[4,5] ...

2012

0.0

... 除钻取方式外,还有火星探测器小猎犬二号采用了锤击贯入方式,欧洲空间局在研的仿生木蜂方式,但以上两种方式只能实现松软对象的浅层刺入^[6,7] ...

2015

0.0

... 除钻取方式外,还有火星探测器小猎犬二号采用了锤击贯入方式,欧洲空间局在研的仿生木蜂方式,但以上两种方式只能实现松软对象的浅层刺入^[6,7] ...

1991

0.0

... 从现有的月球探测图像及地质研究资料^[8]分析,除少数大落差月崖局部有基岩裸露外,月球表面主要由月壤风化物覆盖,已知覆盖深度约10~15 m,远大于现有探测深度3 m ...

2012

0.0

... 但由于月壤颗粒形态及其形成环境条件特殊,在距月表60 cm以下区域月壤密实度会达到90%以上,这导致月壤的流动性较差^[9] ...

1974

0.0

... 临界尺度颗粒是指直径与钻头尺寸相近的月壤颗粒,在月表风化层中临界尺度颗粒数量较少,但对钻头的排屑性能影响明显,会导致钻进负载波动,严重时导致卡钻或者钻具结构损坏^[10] ...

2008

0.0

... 在地表地质钻探取样领域,广泛采用液态水作为排屑及冷却介质,地质钻头构型设计主要考虑回转钻进的稳定性及排屑液导流性能^[11] ...

2005

0.0

... 为实现取样任务,月表次表层取样钻具应当在有限时间和能量供给条件下具备以下几个方面的能力^[12]:①不依赖排屑介质并保证顺畅排屑 ...

2008

0.0

... 比较有代表性的有Apollo系列的平面基体直线切削刃构型和Luna系列的阶梯基体线性排列柱状切削刃构型^[13] ...

2004

0.0

... 此外在在研的火星探测钻具设计中,也大多具有相似特征,例如欧洲空间局的Exomars系列采用浅锥基体直线排屑翼结构,NASA(美国国家航空和宇宙航行局)和JPL(美国喷气推进实验室)合作研发的MSR系列钻具采用的平面基体直线排屑结构^[14,15] ...

2008

0.0

2015

0.0

... 以上多个系列的近地天体取样钻具大多是以岩石破碎为首要目标进行设计的,当钻进对象为月壤及临界尺度颗粒混合物时,存在钻进效率低下且容易发生卡钻的问题^[16] ...

2016

0.0

... 式中: αt为月壤碎屑排屑角,该角度定义为月壤碎屑流动方向与钻头回转线速度方向间的夹角^[17] ...