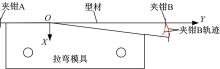
某轨道车辆车身立柱构件如图1所示, 材料为SUS301L-HT不锈钢, 厚度为1.5 mm。可以看出, 该构件尺寸大, 截面呈U型, 且一侧翼边宽度明显大于另一侧。生产中发现该类构件经常出现截面畸变缺陷(见图2), 且轮廓精度差, 导致车身装配精度难以保证。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 宽翼边U型截面不锈钢型材构件几何特征Fig.1 Geometry structure of the U-section stainless steel profile part with wide flange

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 宽翼边U型截面不锈钢构件常见截面畸变缺陷Fig.2 Common section distortion defects of U-section stainless steel parts with wide flange

基于零件特征, 构建如图3所示的不锈钢型材拉弯成形有限元模型。模型包括拉弯模具、夹钳和型材几部分。其中, 型材为可变形壳体, 采用S4R网格类型进行划分, 全局网格尺寸为15 mm, 局部采用1 mm网格进行细化; 夹钳和拉弯模具为不可变形刚体, 采用H3D4网格类型进行划分, 全局网格尺寸为25 mm, 局部采用1 mm网格进行细化。材料模型选取Krupkowsky准则, 屈服准则为Mises准则。摩擦模型选取Coulomb模型, 摩擦因数设置为0.1。材料性能数据如下:密度ρ 为7850 kg/m³; 弹性模量E为188.8 GPa; 泊松比ν 为0.33; 屈服强度σ _s为781.5 MPa; 硬化系数K为1.504 GPa; 应变强化系数n为0.1743。模型中夹钳简化为平面, 型材端部与夹钳绑定。拉弯过程中, 拉弯模具固定不动, 夹钳的转动和移动带动型材包绕拉弯模具完成成形。型材初始立边高度取理论件立边高度, 拉伸量取10%型材长度。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不锈钢型材拉弯成形有限元模型Fig.3 Simulation model for stretch bending of stainless steel profile

拉弯过程中, 型材依靠夹钳的运动包绕拉弯模具弯曲成形。因此, 夹钳的运动轨迹是拉弯成形数值模拟的关键。假设弯曲过程中型材内侧与拉弯模具型面充分接触, 则接触点亦是拉弯模具型面曲线的切点, 于是可基于拉弯模型几何特征构建拉弯过程中夹钳轨迹, 计算公式如下:

XJ=1000sinθ+L+Δl-1000θcosθYJ=10001-cosθ+L+Δl-1000θsinθ1

式中:(X_J, Y_J)为夹钳坐标; L为型材长度; Δ l和θ 分别为型材弯曲过程中的伸长量和转角。

当型材拉伸量为10%型材长度时, 夹钳的运动轨迹如图4所示。图4中, 实线表示夹钳拉弯过程中实际运动轨迹, 虚线表示型材纯弯曲条件下的轨迹, 实线与虚线之前的间隙则为型材的伸长量。此外, 需注意的是, 该夹钳轨迹为图3中夹钳B的轨迹。由于夹钳A侧的型材只伸长不弯曲, 故夹钳A仅横向移动, 不转动。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 夹钳轨迹Fig.4 Jig trajectory

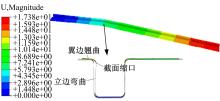
初始模型模拟结果如图5所示。可以看出, 拉弯件立边弯曲, 翼边翘曲, 截面缩口, 发生了明显的截面畸变, 且窄翼边一侧畸变程度明显大于宽翼边一侧。拉弯过程中, 型材轴向伸长。根据体积不变准则, 型材截面收缩。其中, 型材立边的收缩使型材立边高度小于拉弯胎翼边高度, 导致立边弯曲、翼边翘曲, 而立边的向内弯曲导致截面缩口。宽翼边一侧相对窄翼边一侧与模具接触更充分, 由于摩擦力等外力作用更不易变形, 故截面畸变程度相对较小。此外, 拉弯件回弹显著, 最大回弹量达到17.38 mm(要求1 mm以内), 轮廓精度超差。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 拉弯成形模拟结果Fig.5 Simulation results of stretch bending

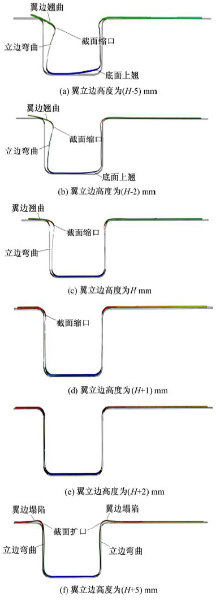
由上述分析可知, 型材立边高度是影响型材拉弯成形截面变形的重要因素。因此, 本文通过补偿型材立边高度的方法对拉弯成形截面畸变缺陷进行控制。拉伸量为10%时, 不同型材立边高度条件下拉弯件的截面变形情况如图6所示, 其中 H为理论件立边高度。由图6(a)(b)可知, 当型材立边高度小于理论件立边高度时, 拉弯件翼边翘曲和截面缩口程度更大, 且出现了底面上翘缺陷, 截面畸变更严重。由图6(d)(e)可知, 随着立边高度补偿量的增加, 截面畸变程度逐渐缩小; 当型材立边高度为(H+2) mm时, 拉弯件截面变形情况良好, 无畸变。然而, 当立边高度补偿量过大时, 会出现翼边塌陷和截面扩口等新的截面畸变缺陷(见图6(f))。因此, 当拉伸量为10%型材长度时, 合理的型材立边高度补偿量为2 mm。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同立边高度时拉弯件截面变形情况Fig.6 Section deformation of bent parts for different profile sidewall heights

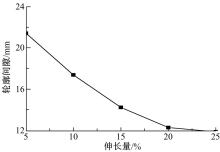
通常采取改善工艺参数或对模具型面进行回弹补偿的方法控制弯曲件的轮廓精度。本文利用数值模拟技术, 对增大拉伸量和基于回弹对模具型面进行修正两种轮廓精度控制方法的效果分别进行分析, 结果如图7和图8所示。可以看出, 一定范围内, 随着拉伸量的增大,

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 轮廓精度随拉伸量的变化Fig.7 Variation of contour accuracy with elongations

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 轮廓精度随模具型面修正量的变化Fig.8 Variation of contour accuracy with die surface modification amounts

拉弯件回弹量有所减小, 轮廓精度有所提高, 但仍然超差; 当拉伸量增大至20%以上时, 继续增大拉伸量轮廓精度改善效果不显著。此外, 增大拉伸量会使型材截面收缩更严重, 截面变形情况更加难以控制。基于回弹修正模具型面对轮廓精度的控制效果显著; 当模具型面修正量为1.3倍回弹量时, 拉弯件轮廓精度良好, 但修正量过大同样会导致成形件轮廓精度超差。因此, 建议使用模具型面修正的方法进行轮廓精度的控制。对本文构件而言, 拉伸量为10%时, 合理的模具型面修正量为1.3倍回弹量。