为了研究不同试验土壤上着陆器足垫冲击特性, 吉林大学工程仿生教育部重点实验室研制了着陆器足垫模型垂直冲击试验系统, 如图1所示。该试验系统主要由土槽、冲击装置和控制采集系统3部分组成。该系统可实现足垫从不同高度沿导轨垂直冲击土槽中试验土壤。土槽尺寸长、宽和高分别为300、300和400 mm; 最大冲击高度和载荷分别为1.5 m和500 N; 最大理论垂直冲击速度约为5 m/s。

冲击装置主要由导轨、起吊平台、电磁铁、冲击平台、足垫模型、标尺、吊索和手轮等组成。起吊平台通过电磁铁将冲击平台吸附, 通过吊索和手轮起吊至预定试验高度后, 电磁铁控制开关关闭电磁铁电源, 启动冲击平台, 足垫模型从静止悬停状态迅速转变为自由落体运动, 沿垂直导向立柱自由下落冲击土槽中土体。

控制采集系统包括加速度传感器(型号为CA-YD-180C, 灵敏度为0.509 mV/(m· s^-2))、移动数据采集器(型号为MDR-81)和控制PC, 其中, 足垫冲击加速度信号通过安装在足垫上方的压电式加速度传感器和移动数据采集器记录, 控制PC用于试验控制、数据采集和存储。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 着陆器足垫冲击试验系统Fig.1 Lander footpad impact test system

本文试验介质共有6种, 如图2所示, 包括:吉林大学研制的面向月面巡视探测器的模拟月壤TYII-1(粗大颗粒)和TYII-2(细小颗粒); 面向火星探测器的JLU Mars-1型模拟火星壤^{[9, 10]}; 采集自敦煌戈壁滩(巡视器试验外场)的戈壁砂壤; 国内外普遍采用的成本较低的石英砂; 同济大学研制的面向月球着陆器的CE-3型模拟月壤^[5]。6种试验土壤中, 模拟月壤和模拟火星壤均以火山灰和火山岩为原料, 通过去除杂质、研磨、筛分、配比加工而成^[9]。石英砂颗粒粒径分布范围较窄, 属于均匀材质, 主要用于对比试验。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 试验土壤Fig.2 Test soils

试验土壤的主要力学性能参数如表1所示, 含水率均不超过1%, 属于干性砂壤。容重范围为土壤自然和密实状态下的上限和下限值, 其中两种状态下CE-3和JLU Mars-1的容重变化较大。中值粒径D₅₀为土壤的累计粒度分布百分数达到50%时所对应的粒径; 不均匀系数C_u用来衡量土壤中颗粒的均匀程度, 若C_u< 5, 则土壤颗粒分布均匀; 曲率系数C_c用来衡量土壤中粒度分配范围形状的指标, 其数值为1~3, 认为土壤的级配是合适的。由表1可知, TYII-2的中值粒径最小, 颗粒总体较细, 石英砂的其次, TYII-1、JLU Mars-1的在200 μ m左右, 戈壁砂壤和CE-3的较大; 4种模拟星壤不均匀系数C_u均大于5, 说明土壤颗粒分布不均匀, 而戈壁砂壤和石英砂则属于相对均匀介质; 6种土壤中仅模拟月壤TYII-2的曲率系数C_c为1~3, 表明其级配较其他土壤的好。

表1

Table 1

表1(Table 1)

表1 试验土壤参数 Table 1 Parameters of test soils 土壤类型 含水率 /% 容重γ /(g· cm-3) 中值粒径 D50/μ m 不均匀系 数Cu 曲率系数 Cc 戈壁砂壤 0.78 1.32~1.47 217 2.85 0.76 石英砂 0.17 1.42~1.49 140 1.79 0.96 TYⅡ -1 0.25 1.29~1.35 202 12.9 0.58 TYⅡ -2 0.32 1.36~1.45 45 6.68 1.56 CE-3 0.22 1.02~1.64 260 21.5 0.92 JLU Mars-1 0.19 0.95~1.13 194.5 5.16 0.94

表1 试验土壤参数 Table 1 Parameters of test soils

(1)足垫直径:考虑到土槽尺寸和足垫边界效应, 基于相似理论足垫采用了缩尺寸模型^[5], 足垫模型采用高度为10 mm的圆板代替, 直径为60~140 mm, 采用等间距5水平。

(2)冲击高度:着陆器在星球表面降落过程中分为减速、悬停和自由下落3个阶段, 其中自由下落阶段为垂直冲击过程, 其初始速度约4 m/s, 对应冲击高度约为800 mm, 因此为考察冲击高度对足垫冲击特性影响, 试验中冲击高度水平还包括600 mm和1000 mm。

(3)土壤状态:土壤在不同密实度下呈现的物理力学特性会对试验产生不同的结果^[11], 综合考虑试验需要以及整备方法的稳定性和效率, 选择2种整备方法, 使得土壤达到自然状态和密实状态2种不同状态, 分别对应表1容重数值的最小值和最大值。

综上所述, 试验因素水平表如表2所示, 试验方案中将土壤种类和状态作为单独考虑的试验因素。6种土壤2种不同状态下对每个试验点进行3次重复试验, 试验总次数为540次。

表2

Table 2

表2(Table 2)

表2 试验因素水平表 Table 2 Levels of factors for soil bin test 因 素 水 平 1 2 3 4 5 足垫模型直径/mm 60 80 100 120 140 冲击高度/mm 600 800 1000 - -

表2 试验因素水平表 Table 2 Levels of factors for soil bin test

为获取足垫冲击深度, 试验前, 降落冲击平台, 使得足垫下表面与土壤平面刚接触, 记录标尺读数; 冲击过程结束后, 再次记下标尺读数, 二者差值则为冲击深度。

为提高测量精度, 冲击加速度信号由对称安装在足垫上方的2个加速度传感器测量, 采样频率为256 Hz, 采集时间为8 s。通过DDP动态信号处理软件(见图3)提取加速度峰值, 取2个加速度传感器均值作为足垫的加速度数值。冲击力峰值则通过瞬时加速度和相互作用时间计算得到。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 加速度数据处理软件Fig.3 Data processing software for acceleration

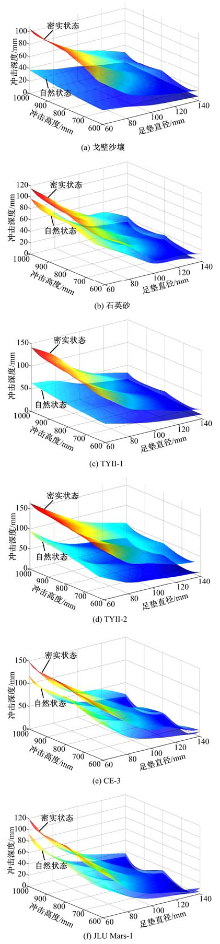
6种土壤试验条件下, 冲击深度随冲击高度和足垫直径变化如图4所示。由图4可知, TYⅡ -1、TYⅡ -2和CE-3型模拟月壤的冲击深度明显较大, JLU Mars-1型模拟火星壤和石英砂的其次, 戈壁砂壤的最小。相同试验条件下, 对比6种土壤冲击深度最大差值达61 mm(自然状态)和79.3 mm(密实状态), 最大值较最小值平均提高了1.49倍(自然状态)和1.09倍(密实状态)。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同土壤条件下冲击深度Fig.4 Impact depth under different testing soil condition

(1)土壤状态对冲击深度的影响

自然状态下, TYⅡ -1、TYⅡ -2和CE-3型模拟月壤的足垫冲击深度最大值明显较其他3种土壤的大, 石英砂和JLU Mars-1型模拟火星壤的其次, 戈壁砂壤的最小; 密实状态下, 最大冲击深度从大到小排序依次为:CE-3、TYⅡ -2、石英砂、JLU Mars-1、TYⅡ -1和戈壁砂壤, 其中戈壁砂壤冲击深度仍为最小。

土壤由自然状态变为密实状态时, 冲击深度的变化率如表3所示。对比发现, 戈壁砂壤、TYⅡ -1和TYⅡ -2的变化率较为明显, 均值达到50%以上, 而CE-3、JLU Mars-1和石英砂的平均变化率约为35%。由于戈壁砂壤为自然条件下形成, 颗粒粒径分布较广, 同样, TYⅡ -1和TYⅡ -2的粒径分布范围较CE-3和JLU Mars-1的大, 而石英砂的颗粒粒径相同属于匀质材料, 因此, 粒径分布较广的土壤, 其冲击深度对土壤状态的变化更为敏感。

表3

Table 3

表3(Table 3)

表3 不同土壤密实度下冲击深度变化率 Table 3 Change rate of impact depth under different soil compactness % 变化率 戈壁砂壤 石英砂 TYⅡ -1 TYⅡ -2 CE-3 JLU Mars-1 最大值 69.42 54.40 59.42 71.93 61.52 46.67 最小值 52.94 15.28 42.22 41.90 17.23 22.84 平均值 60.35 32.27 51.27 61.31 35.69 37.01

表3 不同土壤密实度下冲击深度变化率 Table 3 Change rate of impact depth under different soil compactness %

(2)足垫直径对冲击深度的影响

不同土壤条件下, 冲击深度随着足垫直径的增大逐渐减小。足垫直径的改变主要引起足垫与土壤的接触压强的变化, 试验中足垫直径平均变化率为23.75%, 对应的接触压强平均变化率为34.21%。不同足垫直径条件下, 冲击深度变化率最值和均值如表4所示。6种土壤条件下冲击深度的变化率均值分别为31.28%(自然状态)和33.5%(密实状态), 由此可知, 自然和密实土壤状态下足垫直径的影响不明显。对比表3发现, 足垫直径对冲击深度的影响较土壤状态的小。

表4

Table 4

表4(Table 4)

表4 冲击深度随足垫直径的变化率 Table 4 Change rate of impact depth with footpad diameter % 土壤 状态 戈壁 砂壤 石英砂 TYⅡ -1 TYⅡ -2 CE-3 JLU Mars-1 自然 27.76 34.00 30.07 22.66 36.04 37.16 密实 27.16 40.91 27.16 30.44 35.50 39.84

表4 冲击深度随足垫直径的变化率 Table 4 Change rate of impact depth with footpad diameter %

(3)冲击高度对冲击深度的影响

不同土壤条件下, 冲击深度随着冲击高度的增大而增大。冲击深度随着冲击高度条件变化率最值和均值如表5所示。6种土壤条件下冲击深度的变化率均值为25.40%(自然状态)和30.73%(密实状态), 自然状态下冲击高度的影响更明显。对比表4发现, 足垫直径对冲击深度的影响较冲击高度的大, 平均变化率分别为32.4%和28.1%。

表5

Table 5

表5(Table 5)

表5 冲击深度随足垫直径的变化率 Table 5 Change rate of impact depth with footpad diameter % 土壤 状态 戈壁 砂壤 石英砂 TYⅡ -1 TYⅡ -2 CE-3 JLU Mars-1 自然 27.76 34.00 30.07 22.66 36.04 37.16 密实 27.16 40.91 27.16 30.44 35.50 39.84

表5 冲击深度随足垫直径的变化率 Table 5 Change rate of impact depth with footpad diameter %

综上所述, 相同试验条件下, 6种土壤冲击深度差异明显, TYⅡ -1、TYⅡ -2和CE-3型模拟月壤的冲击深度明显较大; JLU Mars-1型模拟火星壤和石英砂其次; 戈壁砂壤的最小。土壤状态对冲击深度的影响最大, 其次为足垫直径, 冲击高度的影响最小。

冲击高度的改变使得冲击能量发生变化, 本文重点研究冲击高度对足垫冲击加速度的影响。在6种土壤条件下, 足垫直径为100 mm, 冲击高度分别为600、800和1000 mm时, 对足垫冲击的动态加速度数据进行采集。试验中, 足垫冲击能平均变化率为29.17%。

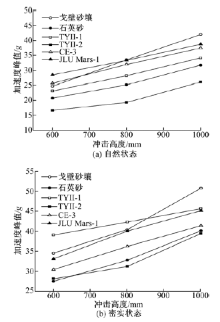
图5为不同土壤条件下加速度峰值随冲击高度的变化规律, 由图5可知, 试验条件下, 加速度峰值为16.7~42g(自然状态)和27.5~50.8g(密实状态), 其中g=9.8 m²/s。不同土壤条件下, 自然和密实状态下加速度峰值均值如表6所示, 土壤由自然状态变为密实状态时, 加速度峰值平均增加率为33.3%。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 加速度峰值随冲击高度变化规律Fig.5 Mean peak acceleration versus with impact height

由表6可知, 自然状态下, TYⅡ -2的加速度峰值最小, 其次为石英砂和TYⅡ -1, JLU Mars-1、戈壁砂壤和CE-3相接近; 密实状态下, 石英砂和YⅡ -2的加速度峰值较小, 其次为CE-3, JLU Mars-1、戈壁砂壤和YⅡ -1的则较大。

表6

Table 6

表6(Table 6)

表6 不同土壤条件下加速度峰值均值 Table 6 Mean peak acceleration under different soil state g 土壤 状态 戈壁 砂壤 石英砂 TYⅡ -1 TYⅡ -2 CE-3 JLU Mars-1 自然 33.4 25.9 28.5 20.7 31.7 33.5 密实 41.9 33.5 42.3 32.9 36.0 39.4

表6 不同土壤条件下加速度峰值均值 Table 6 Mean peak acceleration under different soil state g

试验条件下, 冲击力峰值随冲击高度的变化规律与加速度峰值变化趋势保持一致, 足垫垂直冲击力峰值为1.73~4.22 kN(自然状态)和2.80~5.08 kN(密实状态), 相较于土壤自然状态, 密实状态下冲击力峰值平均提高了32.1%。不同土壤条件下, 冲击力峰值平均值如表7所示。自然和密实状态下, TYⅡ -1和TYⅡ -2的冲击力峰值差异较明显, 而CE-3的则较小。不同土壤状态下, 戈壁砂壤的冲击力峰值始终最大, 主要原因是戈壁砂壤颗粒分布较广, 且存在较大粒径的石块, 在与足垫相冲击的过程中冲击力峰值较大; TYⅡ -2模拟月壤的冲击力峰值始终最小, 原因是由于其颗粒较细, 流动性明显, 能较好的“ 缓冲” 吸收足垫的冲击能。

表7

Table 7

表7(Table 7)

表7 不同土壤条件下冲击力峰值均值 Table 7 Mean peak acceleration under different soil state kN 土壤 状态 戈壁 砂壤 石英砂 TYⅡ -1 TYⅡ -2 CE-3 JLU Mars-1 自然 3.39 2.64 2.89 2.13 3.21 3.38 密实 4.25 3.38 4.21 3.33 3.63 3.97

表7 不同土壤条件下冲击力峰值均值 Table 7 Mean peak acceleration under different soil state kN

基于美国在2013年公开了Apollo探月计划中着陆器着陆时的部分数据, George^[12]给出了月球着陆器足垫受到的垂直力模型如下:

Fv=Kv×A×Zp1

式中: Fv是月壤对足垫的垂直反作用力, N; Kv为承载强度系数, Pa/m; A为足垫面积, m²; Zp为垫的冲击深度, m。参照土体静态承压模型, 引入冲击深度指数 n对模型(1)进行修正:

Fv=K'v×A×Zpn2

式中: K'v为修正的承载强度系数, 与土壤类型和密实度相关, MPa/mm; n为足垫的冲击深度指数, 无量纲。

结合试验数据, 不同试验条件下的模型拟合系数值如表8所示, 相关系数R²均达到0.9以上, 表明修正的冲击力模型能较好地预测足垫冲击力峰值。由表8可知, 承载强度修正系数 K'v范围为1.30~18.32 MPa/mm, 足垫的冲击深度指数 n的范围为0.24~1.33。不同的土壤类型和状态, K'v值变化明显, 与土壤类型和状态对加速度峰值影响规律一致。

表8

Table 8

表8(Table 8)

表8 模型系数值 Table 8 Value of model coefficients 土壤 状态 模型 系数 戈壁 砂壤 石英砂 TYⅡ -1 TYⅡ -2 CE-3 JLU Mars-1 自然 K'v 5.66 2.55 18.32 6.33 12.74 3.35 n 0.58 0.80 0.60 1.33 1.22 1.13 密实 K'v 4.31 5.67 1.30 6.11 6.69 3.94 n 0.52 0.69 0.24 0.74 0.75 0.51

表8 模型系数值 Table 8 Value of model coefficients