基于跟踪微分器的加速度反馈控制

引用本文

申帅, 张葆, 李贤涛, 朱枫, 晋超琼. 基于跟踪微分器的加速度反馈控制. 2017, 47(4): 1217-1224
SHEN Shuai, ZHANG Bao, LI Xian-tao, ZHU Feng, JIN Chao-qiong. Acceleration feedback control based on tracking differentiator. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1217-1224 复制到剪切板

Permissions

基于跟踪微分器的加速度反馈控制

申帅^1,², 张葆¹, 李贤涛¹, 朱枫^1,², 晋超琼^1,²

1.中国科学院长春光学精密机械与物理研究所中国科学院航空光学成像与测量重点实验室,长春 130033

2.中国科学院大学,北京 100049

通讯作者：张葆(1966-),男,研究员,博士.研究方向:航空光电成像技术.E-mail:zcleresky@vip.sina.com

作者简介:申帅(1991-),男,博士研究生.研究方向:航空光电稳定平台视轴稳定.E-mail:shenshuaiharry@163.com

基金:“863”国家高技术研究发展计划重点项目(2013AA122102).

摘要

为了提高航空光电稳定平台的抗扰性的同时不增加平台成本,本文在传统平台的电流反馈、速度反馈、位置反馈系统的基础上增加基于跟踪微分器的高增益加速度反馈环节,相对于传统基于差分的加速度反馈系统,基于跟踪微分器的加速度反馈系统改善了其对噪声干扰敏感等问题。通过模拟转台,对平台进行1°、0~2.5 Hz正弦扰动测试,结果表明:相对于传统速度反馈平台系统,基于跟踪微分器的加速度反馈系统,超调量减小了约4.9%,视轴稳定精度提高了至少63.4%,平台的过渡过程加快;且该伺服系统结构简单,有较好通用性和实用价值。

关键词: 自动控制技术; 抗扰性; 加速度反馈; 跟踪微分器; 视轴稳定精度

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2017)04-1217-08

Acceleration feedback control based on tracking differentiator

SHEN Shuai^1,², ZHANG Bao¹, LI Xian-tao¹, ZHU Feng^1,², JIN Chao-qiong^1,²

1.Key Laboratory of Airborne Optical Imaging and Measurement, Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

2.University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

In order to improve the noise immunity of airborne optoelectronic stabilization platform and save cost, high-gain acceleration feedback by utilizing the tracking differentiator is studied based on current feedback, speed feedback and position feedback on a traditional platform. Compared with the traditional differential acceleration feedback system, the acceleration feedback system based on the tracking differentiator reduces the sensitivity to noise interference. The stabilization platform is tested with one degree, 0~2.5 Hz sinusoidal interference on a flight simulator. Results show that, compared with the traditional speed platform feedback system, the acceleration feedback system based on the tracking differentiator can reduce the overshoot by 4.9%, increase LOS stabilization accuracy at least by 63.4% and improve the transition process of the platform greatly. Besides, the servo system has simple structure, better generality and higher practical value.

Keyword: automatic control technology; noise immunity; acceleration feedback; tracking differentiator; LOS stabilization accuracy

Show Figures

0 引言

航空光电稳定平台主要挂载于直升侦察机底部的吊舱中, 其作用是实现恶劣环境条件下对目标的精确瞄准和稳定跟踪。直升机侦查过程中的振动、载体姿态的变化以及大气紊流等因素都将直接导致光电载荷平台的视轴指向不稳定, 而平台工作过程中的启动、制动都要求其超调量尽量不超过目标值的20%^[1], 因而平台需要较强的抗扰性, 来提高平台的视轴稳定精度。

目前国内外的航空光电稳定平台主要采用传统电流反馈、速度反馈、位置反馈的三闭环控制模式^[2], 没有从根本上, 即从力矩作用角度对扰动进行衰减; 一些利用加速度反馈的平台大都利用差分陀螺速度或直接用线加速度计组合的方式来获取加速度, 以达到直接衰减扰动力矩的目的, 但是差分陀螺速度所获得加速度信号受噪声的影响相对较大, 而高精度加速度计造价昂贵^[3], 一些小型平台负担不起这样的成本。

通过将基于跟踪微分器的加速度反馈环节引入到传统电流反馈、速度反馈、位置反馈调节的平台系统中可以使平台的扰动抑制能力大幅上升。文中航空光电稳定平台系统利用增加开关区域线性区宽度的最速控制跟踪微分器来获取加速度信号, 以搭建加速度反馈环节, 兼顾了加速度信号的快速性和抗扰性, 并以较低成本基本达到了与基于加速度计的加速度反馈系统的同等抗扰水平。从而实现了在不增加平台成本的基础上提高平台抗扰性的目的。

1 加速度反馈优势、原理及抗扰性分析

1.1 加入加速度反馈的优势

传统航空光电稳定平台采用电流反馈、速度反馈、位置反馈的三闭环控制模式, 其中电流反馈的目的主要是为了给外环带来足够的相位裕度, 提高系统的响应速度, 同时使得电机不再受到电子噪声即反电动势的影响, 从而使得力矩和电机呈线性关系^[4]。如果没有高带宽的电流环, 力矩不会很快由电流产生, 而是受到反电势的影响会慢一些。

电流反馈的引入实际上使电机在加速度反馈环节内变成一个理想的比例环节, 而如果没有加速度反馈环节, 则电流环会使电机在速度环内变成一个理想的积分环节^[5]。从物理学的角度, 根据力矩和加速度的关系可知, 当平台各部件确定后其质量是一定的, 因而力矩与加速度是线性关系, 对加速度进行操作相当于直接从力矩的角度对干扰进行衰减。而如果没有加速度环, 只用对速度环进行调控, 则相当于对加速度的积分进行操作。在扰动抑制方面, 相对于直接对加速度进行操作已经有了一定时间的延迟和误差积累, 由此可见采用加速度反馈的优越性。

1.2 加速度反馈的基本原理

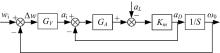
带有加速度反馈的航空光电稳定平台系统闭环原理图(在这里没有画出位置环)如图1所示。

	Figure Option View Download New Window
	图1 将加速度反馈环节引入平台系统后的系统框图Fig.1 Block diagram of platform system containing acceleration feedback loop

图1中, $\begin{matrix} G_{V} \end{matrix}$ 为速度环控制器; $\begin{matrix} G_{A} \end{matrix}$ 为加速度环控制器; $\begin{matrix} a_{D} \end{matrix}$ 为电机输出力矩产生的加速度; $\begin{matrix} a_{L} \end{matrix}$ 为扰动力矩在电机轴系上产生的扰动加速度; $\begin{matrix} K_{m} \end{matrix}$ 为电流环比例系数; $\begin{matrix} w_{i} \end{matrix}$ 为输入角速率; $\begin{matrix} w_{o} \end{matrix}$ 为输出角速率; $\begin{matrix} a_{i} \end{matrix}$ 为输入角加速度。

电机正常工作时:

$\begin{matrix} T = F \times D = C \times φ \times I \times D (1) \end{matrix}$

式中: $\begin{matrix} T \end{matrix}$ 表示电机力矩; $\begin{matrix} F \end{matrix}$ 表示电磁力; $\begin{matrix} D \end{matrix}$ 表示半径; $\begin{matrix} φ \end{matrix}$ 表示电机磁通; $\begin{matrix} C \end{matrix}$ 表示电机常数; $\begin{matrix} D \end{matrix}$ 表示电机转矩。电机正常工作时 $\begin{matrix} C 、 D 、 φ \end{matrix}$ 均为常数, 设 $\begin{matrix} K \end{matrix}$ 为 $\begin{matrix} C 、 D 、 φ \end{matrix}$ 的乘积, 则有: $\begin{matrix} T = KI 。 \end{matrix}$ 再根据力矩和加速度的关系有:

$\begin{matrix} T = m \overset{\cdot}{ω} (2) \end{matrix}$

式中: $\begin{matrix} m \end{matrix}$ 表示平台质量; $\begin{matrix} \overset{\cdot}{ω} \end{matrix}$ 表示角加速度。

在加速度环内进行拉氏域变换有:

$\begin{matrix} KI = m \overset{\cdot}{ω} (s) (3) \end{matrix}$

将 $\begin{matrix} KI \end{matrix}$ 按比例与系统电压 $\begin{matrix} U (s) \end{matrix}$ 等效可知加速度输出 $\begin{matrix} \overset{\cdot}{ω} (s) \end{matrix}$ 与输入电压 $\begin{matrix} U (s) \end{matrix}$ 的关系为:

$\begin{matrix} \frac{\overset{\cdot}{ω} (s)}{U (s)} = K_{m} (4) \end{matrix}$

式中: $\begin{matrix} K_{m} \end{matrix}$ 为综合了系统的电压与力矩的比例以及 $\begin{matrix} K 、 m \end{matrix}$ 关系的电流环比例系数。

扰动本身就是一种力矩作用设为 $\begin{matrix} F \end{matrix}$ , 平台的质量 $\begin{matrix} m \end{matrix}$ 是确定的, 则在扰动力矩经过电流环后在加速度环内同样表现为一个跟随外部环境实时变化的扰动加速度 $\begin{matrix} a_{L}, \end{matrix}$ 对于稳定平台来说, 就是期望扰动力矩产生的 $\begin{matrix} a_{L} \end{matrix}$ 与输出 $\begin{matrix} w_{o} \end{matrix}$ 的比值越小越好。

1.3 加速度反馈对系统扰动抑制及稳定性的影响

1.3.1 加速度反馈对系统扰动抑制的影响

在航空光电稳定平台中引入加速度反馈后, 其对扰动的抑制能力显著提高。

传统速度反馈调节系统, 在理想情况下转台速度环简化框图如图2所示。

	Figure Option View Download New Window
	图2 传统速度反馈系统简化框图Fig.2 Simplified block diagram of classical speed feedback system

由图2知, 扰动加速度对速率的影响结果可以表示为:

$\begin{matrix} Δ w_{o} = \frac{K_{m}}{s + G_{V} K_{m}} a_{L} (5) \end{matrix}$

基于加速度反馈的闭环调节系统在理想情况下系统速度环简化框图如图1所示, 扰动加速度对速率的影响结果可以表示为:

$\begin{matrix} Δ w_{o} = \frac{K_{m}}{s [1+ G_{A} K_{m}] + G_{V} G_{A} K_{m}} a_{L} (6) \end{matrix}$

显然对于式(5)(6)满足:

$\begin{matrix} |s + G_{V} K_{m}| ≪ |s [1+ G_{A} K_{m}] + G_{V} G_{A} K_{m}| (7) \end{matrix}$

从频域角度出发, 引入加速度反馈后, 力矩干扰产生的扰动加速度 $\begin{matrix} a_{L} \end{matrix}$ 经过加速度反馈环节后的速率波动将大幅度减小。

1.3.2 加速度反馈对系统稳定性的影响

由图1可以得到带有加速度反馈闭环的速度环输出为:

$\begin{matrix} \begin{matrix} w_{o} = \frac{G_{V} G_{A} K_{T}}{s [1+ G_{A} K_{m}] + G_{V} G_{A} K_{m}} w_{i} + \\ \frac{K_{m}}{s [1+ G_{A} K_{m}] + G_{V} G_{A} K_{m}} a_{L} (8) \end{matrix} \end{matrix}$

在这里加速度闭环采用高增益控制方法^{[6, 7]}, 则系统特征方程为:

$\begin{matrix} s [1+ G_{A} K_{m}] + G_{V} G_{A} K_{m} = 0 (9) \end{matrix}$

在式(9)中加速度反馈环节采用高增益的PI控制方式, 速度环控制器同样也采用经典的PI控制方式, 则由劳斯判据可知, 引入加速度反馈的平台控制系统稳定。

1.4 加速度反馈存在的问题

1.4.1 差分速度获取加速度的弊端

在传统的电流反馈、速度反馈、位置反馈的基础上增加加速度反馈, 虽然可以在很大程度上提升系统的稳定性和抗扰性, 但是目前对于加速度信号的获取还存在一定的困扰。首先是传统差分陀螺速度获取加速度信号的方式, 对噪声信号敏感, 容易造成原始信号失真。这样当被测信号不能连续被系统接收时, 或者被测信号在接收过程中受到严重的噪声污染时, 通过差分方式所得到的加速度信号一般都不能被工程应用。这时如果想利用这个加速度信号的最直接办法就是使接收到的信号再经过低通滤波器, 滤除噪声干扰。但是滤波器的加入会使原始信号在时间上有一定的延迟, 这种延迟在对跟踪性能要求较高的航空光电稳定平台系统中是难以被接受的。

1.4.2 加速度计获取加速度获的限制

如果利用加速度计获取加速度信号, 虽然加速度计安装方便、精度高, 但是造价昂贵, 一些小型的平台系统负担不起这样昂贵的成本。图3分别是常见的单轴、两轴、三轴加速度计。

	Figure Option View Download New Window
	图3 单轴、两轴、三轴加速度计Fig.3 Single axis, two axis, three axis accelerometer

加速度计的价格与其精度的高、低和测量方向的多少成正比, 其中能够满足平台需求的高精度加速度计的市场价格大约是3~4万元, 一些小型平台难以负担如此高的成本。针对以上问题, 作者提出了一种利用跟踪微分器获取加速度的方法。

2 利用跟踪微分器获取加速度信号

2.1 跟踪微分器的基本原理

由于传统获得加速度的两种方法各自存在其弊端:加速度计价格昂贵、差分速度对噪声敏感。韩京清教授^[8]于1994年, 提出了非线性跟踪微分器的全新理论。其中跟踪微分器巧妙的利用数值积分来代替传统的数值微分, 这样微分作用对噪声的敏感问题就被巧妙地回避了。根据跟踪微分器的理念就可以用对微分方程求积分的方式来求解本来要获取的微分信号, 以达到对任意信号求微分的目的。

跟踪微分器的工作流程^[9]:输入信号 $\begin{matrix} v (t) \end{matrix}$ 经过跟踪微分器后将输出两个信号 $\begin{matrix} z_{1} \end{matrix}$ 和 $\begin{matrix} z_{2}, \end{matrix}$ 其中 $\begin{matrix} z_{1} \end{matrix}$ 跟踪 $\begin{matrix} v (t), z_{2} = {\overset{\cdot}{z}}_{1}, \end{matrix}$ 从而把 $\begin{matrix} z_{2} \end{matrix}$ 作为 $\begin{matrix} v (t) \end{matrix}$ 的“ 近似微分” 。

二阶 $\begin{matrix} TD \end{matrix}$ 描述如下:若系统(10)的任意解均满足: $\begin{matrix} z_{1} (t) \to 0, z_{2} (t) \to 0 (t \to \infty), \end{matrix}$ 则对任意有界可积函数 $\begin{matrix} v (t) \end{matrix}$ 和任意常数 $\begin{matrix} T > 0, \end{matrix}$ 系统(11)的解 $\begin{matrix} x_{1} (t) \end{matrix}$ 满足式(12)。

$\{\begin{matrix} {\overset{\cdot}{z}}_{1} = z_{2} \\ {\overset{\cdot}{z}}_{2} = f (z_{1}, z_{2}) \end{matrix} (10)$

$\{\begin{matrix} {\overset{\cdot}{x}}_{1} = x_{2} \\ {\overset{\cdot}{x}}_{2} = R^{2} f (x_{1} - v, \frac{x_{2}}{R}) \end{matrix} (11)$

$\lim_{R \to \infty} \int_{0}^{T} |x_{1} (t) - v (t)| dt = 0 (12)$

式中: $\begin{matrix} R \end{matrix}$ 为跟踪速度因子; $\begin{matrix} x_{1} (t) \to v (t), x_{2} (t) \to \overset{\cdot}{v} (t) 。 \end{matrix}$

2.2 几种跟踪微分器的比较

在式(11)中的综合函数 $\begin{matrix} f \end{matrix}$ 的基础上, 跟踪微分器得到了广泛的发展。为了更好地了解跟踪微分器的性能, 下面对几种常用的跟踪微分器进行分析对比。

(1)开关型跟踪微分器^[8]

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = x_{2} \\ {\overset{\cdot}{x}}_{2} = - Rsign (x_{1} - v (t) + \frac{|x_{2}| x_{2}}{2 R}) \end{matrix} (13) \end{matrix}$

此类跟踪微分器结构较为简单、参数设置少、调节也比较方便, 但由于符号函数sign(· )的存在, 在原点附近会存在颤振现象。

(2)快速非线性跟踪微分器^[10]

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = x_{2} \\ {\overset{\cdot}{x}}_{2} = [\frac{}{} - R^{2} (a_{0} (x_{1} - v) - \\ a_{1} (x_{1} {- v)}^{m / n} - b_{0} \frac{x_{2}}{R} - b_{1} {(\frac{x_{2}}{R})}^{m / n}] \end{matrix} (14) \end{matrix}$

式中: $\begin{matrix} a_{0} 、 a_{1} 、 b_{0} 、 b_{1} \end{matrix}$ 均大于0, $\begin{matrix} m 、 n \end{matrix}$ 为大于0的奇数, 且 $\begin{matrix} m < n \end{matrix}$ 时, 系统在原点处是渐进稳定的。此类跟踪微分器在远离平衡点处, 引入的线性环节起主导作用; 在接近平衡点附近时, 引入的非线性环节起主导作用, 从而使系统状态始终保持快速收敛状态。但参数选取比较困难, 一旦选取不当就会出现发散现象。

(3)离散线性跟踪微分器^[11]

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = x_{2} \\ {\overset{\cdot}{x}}_{2} = - R^{2} [a_{1} (x_{1} - v) - a_{2} \frac{x_{2}}{R}] \end{matrix} (15) \end{matrix}$

式中: $\begin{matrix} a_{1} 、 a_{2} \end{matrix}$ 均大于0, 且 $\begin{matrix} a_{2} = 2 a_{1} \end{matrix}$ 时, 离散线性跟踪微分器是收敛和稳定的, 但失去了由非线性效应带来的快速性, 其跟踪效率较低, $\begin{matrix} R \end{matrix}$ 为决定跟踪快慢的参数, 可适当取大 $\begin{matrix} R \end{matrix}$ 值, 以缩短跟踪过渡过程。

(4)离散最速型跟踪微分器^[12]

$\begin{matrix} \{\begin{matrix} x_{1} (k + 1) = x_{1} (k) + h \times x_{2} (k) \\ x_{2} (k + 1) = x_{2} (k) + h \times fs t_{2} (x_{1} (k) - \\ v (k), x_{2} (k), R, h) \end{matrix} (16) \end{matrix}$

式中: $\begin{matrix} h \end{matrix}$ 为采样周期; $\begin{matrix} v (k) \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 时刻的输入信号。 $\begin{matrix} fs t_{2} (\cdot) \end{matrix}$ 函数为最速控制函数, 描述如下:

$fs t_{2} (x_{1}, x_{2}, R, h) = \{\begin{matrix} - Rsign (a), |a| > d \\ - R \frac{a}{d}, |a| \leq d \end{matrix} (17)$

$\begin{matrix} \begin{matrix} a = \{\begin{matrix} x_{2} + \frac{a_{0} - d}{2} sign (y), |y| > d_{0} \\ x_{2} + y / h, |y| \leq d_{0} \end{matrix} (18) \end{matrix} \end{matrix}$

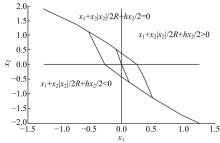
式中:d=Rh, d₀=hd, y=x₁+hx₂, $\begin{matrix} a_{0} = \sqrt[]{d^{2} + 8 R |y|}, \end{matrix}$ 如图4所示。

	Figure Option View Download New Window
	图4 最速函数分布图Fig.4 Distribution map of the most velocity function

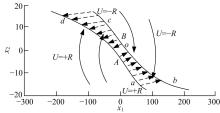
此类跟踪微分器是在二阶系统最速控制的基础上, 采用“ 等时区法” 推导得到的, 其线性区间的大小可直接确定, 它能够快速无超调地对输入信号进行跟踪, 在微分品质、消颤现象等方面也有很好的效果, 只是在形式上稍显复杂。在输入信号受噪声污染或 $\begin{matrix} R \end{matrix}$ 较大时, 输出的微分信号容易被污染。

2.3 利用跟踪微分器获取加速度信号的实现

比较以上4种跟踪微分器可得出, 跟踪微分器设计所追求的目标是:简洁、快速、无振荡、具备滤波功能且调参方便。根据文献[8]可知, 最速控制结构可以有效地解决大多数跟踪微分器微分信号获取速度慢以及参数调节复杂的问题; 如果在跟踪微分器的开关线附近, 加大线性区的宽度可以有效地减小系统震荡, 而且根据线性区边界形状的不同, 跟踪微分器所表现出的性能也会有很大的不同^{[13, 14]}。

综上所述, 如果在一定范围内合理增加控制函数线性区的宽度, 线性区的运动速度就会降低, 而且会使得跟踪微分器对输入信号的滤波作用增强, 从而使得即使输入信号受到严重的噪声污染, 在经过跟踪微分器后, 所获得的微分信号依然能很好地复现原始信号。因此本文选取一个线性区宽度可变的控制函数:

$\begin{matrix} \begin{matrix} f (x_{1}, x_{2}, R, h, n) = \\ x_{2} + s \sqrt[]{\frac{n^{2} h^{2} R^{2}}{4} + |Ry|} - s \frac{n h R}{2} (19) \end{matrix} \end{matrix}$

式中: $\begin{matrix} y = (n + 1) h x_{2} + 2 x_{1}, s = sign (y), \end{matrix}$ 使得线性区上边界满足 $\begin{matrix} f (x_{1}, x_{2}, R, h, n) = n h R, \end{matrix}$ 上边界以上区域的点满足 $\begin{matrix} f (x_{1}, x_{2}, R, h, n) > n h R, \end{matrix}$ 下边界上的点满足 $\begin{matrix} f (x_{1}, x_{2}, R, h, n) = - n h R, \end{matrix}$ 在下边界以下的区域满足 $\begin{matrix} f (x_{1}, x_{2}, R, h, n) < - n h R, \end{matrix}$ 如图5所示。

	Figure Option View Download New Window
	图5 新设计的线性区Fig.5 Newly designed linear region

根据开关系统的特点可取控制综合函数为: $\begin{matrix} u = - R \times sat (f (x_{1}, x_{2}, R, h, n), n h R), \end{matrix}$ 在函数线性区域的内部取 $\begin{matrix} u = f (x_{1}, x_{2}, R, h, n); \end{matrix}$ 在函数线性区域下边界以外的区域, 取 $\begin{matrix} u = + R; \end{matrix}$ 在函数线性区域上边界以外的区域, 取 $\begin{matrix} u = - R 。 \end{matrix}$

由控制综合函数构造出的跟踪微分器如下:

$\{\begin{matrix} x_{1} (k + 1) = x_{1} (k) + h \times x_{2} (k) \\ x_{2} (k + 1) = x_{2} (k) + h \times R \times sa t_{2} (z (k), nhR) \end{matrix} (20)$

$z (k) = x_{2} (k) + s \sqrt[]{\frac{n^{2} h^{2} R^{2}}{4} + |Ry|} - s \frac{nhR}{2} (21)$

$\{\begin{matrix} s = sign (y (k)) \\ y (k) = (n + 1) h x_{2} (k) + 2 x_{1} (k) - v (k) \end{matrix} (22)$

式中: $\begin{matrix} n \end{matrix}$ 为调节线性区宽度的参数。可以看出离散跟踪微分器具有更加简洁的形式, 而且调节参数 $\begin{matrix} n \end{matrix}$ 可以实现对输入信号的滤波。

陀螺速度信号经过此跟踪微分器可以获得品质较好的加速度信号, 在一定程度上克服了传统差分获取加速度存在的对噪声敏感的问题, 但当 $\begin{matrix} R \end{matrix}$ 取较大数值时会出现一定程度相位延时, 因此在合理选取 $\begin{matrix} R \end{matrix}$ 值的情况下, 所获得的加速度品质基本达到了与利用加速度计获取加速度的同一水准, 大大节约了平台的成本。

将利用跟踪微分器获得的加速度作为加速度反馈环节中反馈回路的加速度, 再结合上文提到的对加速度反馈的设计方案, 实现了对扰动力矩产生的加速度的衰减, 也相当于直接对扰动力矩进行了衰减, 这样扰动力矩在经加速度反馈环节时就能被大幅衰减, 再经过外层速度环以及位置环对扰动进行衰减, 最后输出的速度信号或者位置信号所受到的干扰基本可以忽略不计。

3 实验验证

为了验证将基于跟踪微分器的加速度反馈环节引入传统平台控制系统后的伺服性能及效果, 将航空光电稳定平台安装在模拟直升机运动的摇摆台上进行实验, 摇摆台如图6所示。

	Figure Option View Download New Window
	图6 模拟飞机姿态变化的摇摆台Fig.6 Swing table simulation on aircraft attitude change

3.1 与传统速度反馈系统的对比

为了比较基于跟踪微分器的加速度反馈系统和传统的速度反馈系统对扰动的抑制能力, 在1° 、0~2.5 Hz的正弦干扰下, 对系统进行抗扰对比实验, 如表1所示。

表1 视轴稳定精度的提高程度 Table 1 Improvement of LOS stabilization accuracy

如果用LSAD表示基于跟踪微分器的加速度反馈系统的视轴稳定精度, LSAS表示传统速度反馈系统的视轴稳定精度, 则:

$\begin{matrix} LSADS = \frac{LSAS - LSAD}{LSAS} \times 100 % (23) \end{matrix}$

在1° 、2 Hz的正弦干扰下, 视轴波动曲线如图7所示。为了更清楚地比较两系统对扰动的抑制能力, 对图7做频谱分析, 结果如图8所示。

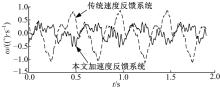	Figure Option View Download New Window
	图7 传统速度反馈系统与本文加速度反馈系统的抗扰曲线Fig.7 Disturbance rejection curve of traditional speed feedback system and proposed acceleration feedback system

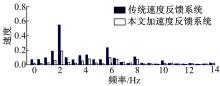	Figure Option View Download New Window
	图8 传统速度反馈系统与本文加速度反馈系统的抗扰曲线频谱分析Fig.8 Frequency spectrum analysis of disturbance rejection curve drawn by traditional speed feedback system and proposed acceleration feedback system

从表1及图7、图8中可以看出:相对于传统速度反馈系统, 基于跟踪微分器的加速度反馈系统在各个频率对扰动均有很好的抑制作用, 扰动抑制能力明显优于传统速度反馈系统。图9是在1° 、2 Hz的正弦干扰下, 给定10° /s的阶跃响应曲线。

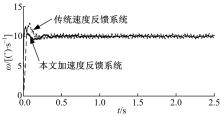	Figure Option View Download New Window
	图9 传统速度反馈系统与本文加速度反馈系统的阶跃曲线Fig.9 Step curve of traditional speed feedback system and proposed acceleration feedback system

从图9中可看出, 相对于传统速度反馈系统, 基于跟踪微分器的加速度反馈系统的超调量从22.5%减小到了16.7%, 过渡过程提速约0.1 s, 从而使相位裕度变大, 提高了系统的稳定性。

3.2 与基于差分的加速度反馈系统的对比

图10是平台以ω =10sin(6π t)角速度转动时的加速度信号曲线。

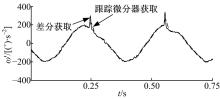	Figure Option View Download New Window
	图10 基于差分与跟踪微分器的加速度反馈的加速度信号Fig.10 Acceleration signal based on differential acceleration feedback system and acceleration feedback system based on tracking differentiator

从图10可以看出:两种获取加速度的方式在相位上基本上相同, 但是差分获取的加速度有较大的尖峰和比较多的毛刺信号, 这对于调节系统是很不利的, 而跟踪微分器获取的加速度信号相对来说尖峰小、曲线平滑、对噪声有较好的抑制能力。

表2是在1° 、0~2.5 Hz的正弦干扰下, 基于跟踪微分器与基于差分的加速度反馈系统抗扰性能的对比实验。

表2 视轴稳定精度的提高程度 Table 2 Improvement of LOS stabilization accuracy

如果用LSAC表示基于差分的加速度反馈系统的视轴稳定精度, 则:

$\begin{matrix} LSADC = \frac{LSAC - LSAD}{LSAC} \times 100 % (24) \end{matrix}$

图11是在1° 、2 Hz的正弦干扰下, 视轴的波动曲线。

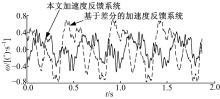	Figure Option View Download New Window
	图11 基于差分与跟踪微分器的加速度反馈系统的抗扰曲线Fig.11 Disturbance rejection curve of differential acceleration feedback system and acceleration feedback system based on tracking differentiator

表2和图11表明基于跟踪微分器的加速度反馈系统的抗扰性明显优于基于差分的加速度反馈系统。

3.3 与基于加速度计的加速度反馈系统的对比

在1° 、0~2.5 Hz的正弦干扰下, 相对于基于跟踪微分器的加速度反馈系统, 基于加速度计的加速度反馈系统视轴稳定精度的提高程度如表3所示。

表3 视轴稳定精度的差值 Table 3 Difference of LOS stabilization accuracy

如果用LSAA表示基于加速度计的加速度反馈系统的视轴稳定精度, 则:

$\begin{matrix} LSAAD = \frac{LSAD - LSAA}{LSAD} \times 100 % (25) \end{matrix}$

根据上述数据知, 相对基于加速度计的加速度反馈系统, 基于跟踪微分器的加速度反馈系统的视轴稳定精度虽稍差, 但其差值都保持在10%左右, 是可接受的。

图12是在1° 、2 Hz的正弦干扰下, 基于跟踪微分器与基于加速度计的加速度反馈系统抗扰实验图。

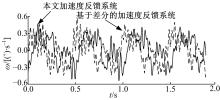	Figure Option View Download New Window
	图12 基于加速度计与跟踪微分器的加速度反馈系统的抗扰曲线Fig.12 Disturbance rejection curve of acceleration feedback system based on accelerometer and acceleration feedback system based on tracking differentiator

表3和图12表明两者的视轴稳定精度相对于传统速度反馈系统基本达到同一水平。图13是在1° 、2 Hz的正弦干扰下, 给定角速度为ω =10sin(6π t)时的对比实验曲线。

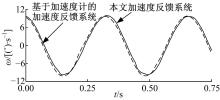	Figure Option View Download New Window
	图13 基于加速度计与跟踪微分器的加速度反馈系统的正弦曲线Fig.13 Sine curve of acceleration feedback system based on accelerometer and acceleration feedback system based on tracking differentiator

从图13中可以看出, 基于跟踪微分器的加速度反馈系统相对于基于加速度计的反馈系统约有2.5 ms滞后, 但相位裕度的减小量可忽略不计, 对于平台跟踪的目标信号, 这种滞后在允许范围内。抗干扰能力虽不如基于加速度计的加速度反馈系统, 但在允许范围内两者基本处于同一水平。在工程实践中利用跟踪微分器来获取加速度信号, 将大大降低以往利用加速度计获取加速度信号的成本。

4 结束语

基于跟踪微分器的加速度反馈控制摒弃了传统基于差分和加速度计获取加速度的方法, 而是以跟踪微分器获取加速度作为反馈。实验结果表明, 将基于跟踪微分器的加速度反馈环节引入到传统航空光电稳定平台系统后, 相对于传统速度反馈系统, 基于跟踪微分器的加速度反馈系统超调量减小了约4.9%, 视轴稳定精度提高了至少63.4%, 平台的过渡过程加快。新的伺服系统结构简单、性能优越, 具有较好的通用性和实用价值。在传统平台系统中引入基于跟踪微分器的加速度反馈环节后, 对外层速度环、位置环等反馈环节的影响基本可以忽略不计, 且新的航空光电稳定平台系统的扰动抑制能力大幅提升, 从而平台的视轴能更好地稳定在惯性空间内。而且基于跟踪微分器的加速度反馈控制系统的性能基本达到了与基于加速度计的加速度反馈系统的同等水准, 可在工程应用中利用跟踪微分器代替加速度计获取加速度信号, 从而大大降低实际平台系统的使用成本, 使小型平台拥有更广阔的发展前景。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	胡松涛. 自动控制原理[M]. 5版. 北京: 科学出版社, 2007: 76-93. [本文引用:1]
[2]	魏伟, 戴明, 李嘉全, 等. 航空光电稳定平台的自抗扰控制系统[J]. 光学精密工程, 2015, 23(8): 2296-2305. Wei Wei, Dai Ming, Li Jia-quan, et al. ADRC control system for airborne opto-electronic platform[J]. Optics and Precision Engineering, 2015, 23(8): 2296-2305. [本文引用:1]
[3]	吴校生, 陈文元. 角加速度计发展综述[J]. 中国惯性技术学报, 2007, 15(4): 458-463. Wu Xiao-sheng, Chen Wen-yuan. Review on angular accelerometer development[J]. Journal of Chinese Inertial Technology, 2007, 15(4): 458-463. [本文引用:1]
[4]	李贤涛, 张葆, 赵春蕾, 等. 基于自适应的自抗扰控制技术提高扰动隔离度[J]. 吉林大学学报: 工学版, 2015, 45(1): 202-208. Li Xian-tao, Zhang bao, Zhao Chun-lei, et al. Improve isolation degree based on adaptive active disturbance rejection controller[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(1): 202-208. [本文引用:1]
[5]	申帅, 张葆, 李贤涛, 等. 航空光电稳定平台质量不平衡力矩的前馈补偿[J]. 光学精密工程, 2017, 25(5): 1281-1290. Shen Shuai, Zhang Bao, Li Xian-tao, et al. Feedforward compensation of mass unbalance moment for airborne photoelectric stabilized platform[J]. Optics and Precision Engineering, 2017, 25(5): 1281-1290. [本文引用:1]
[6]	De Jager B. Acceleration assisted tracking control[J]. IEEE Control Systems, 1994, 14(5): 20-27. [本文引用:1]
[7]	Zhu W H, Tryggvason B, Piedboeuf J C. On active acceleration control of vibration isolation systems[J]. Control Engineering Practice, 2006, 14(8): 863-873. [本文引用:1]
[8]	韩京清. 自抗扰控制技术[J]. 前沿科学, 2007, 1(1): 24-31. Han Jing-qing. Active disturbance rejection control technique[J]. Frontier Science, 2007, 1(1): 24-31. [本文引用:2]
[9]	韩京清, 王伟. 非线性跟踪-微分器[J]. 系统科学与数学, 1994, 14(2): 177-183. Han Jing-qing, Wang Wei. Nonlinear tracking-differentiator[J]. Systems Science and Mathematical Science, 1994, 14(2): 177-183. [本文引用:1]
[10]	王新华, 陈增强, 袁著祉. 全程快速非线性跟踪-微分器[J]. 控制理论与应用, 2003, 20(6): 875-878. Wang Xin-hua, Chen Zeng-qiang, Yuan Zhu-zhi. Nonlinear tracking-differentiator with high speed in whole course[J]. Control Theory and Applications, 2003, 20(6): 875-878. [本文引用:1]
[11]	杨丽君, 卢志刚. 三阶线性跟踪-微分器的收敛性证明及仿真研究[J]. 燕山大学学报, 2006, 30(1): 44-47. Yang Li-jun, Lu Zhi-gang. Proof of a third-order tracking differentiator's convergence and simulation of its dynamic characteristics[J]. Journal of Yanshan University, 2005, 30(1): 44-47. [本文引用:1]
[12]	韩京清, 袁露林. 跟踪-微分器的离散形式[J]. 系统科学与数学, 1999, 19(3): 268-273. Han Jing-qing, Yuan Lu-lin. Discrete tracking differentiator[J]. Systems Science and Mathematical Science, 1999, 14(3): 268-273. [本文引用:1]
[13]	Tian D, Shen H, Dai M. Improving the rapidity of nonlinear tracking differentiator via feedforward[J]. IEEE Transactions on Industrial Electronics, 2014, 61(7): 3736-3743. [本文引用:1]
[14]	彭建亮, 孙秀霞, 董文瀚, 等. 利用跟踪-微分器构造增广比例导引律[J]. 应用科学学报, 2009, 27(4): 435-440. Peng Jian-liang, Sun Xiu-xia, Dong Wen-han, et al. Construction of augmented proportion navigation law with tracking differentiator[J]. Journal of Applied Science—Electronics and Information Engineering, 2009, 27(4): 435-440. [本文引用:1]

2007

0.0

... 直升机侦查过程中的振动、载体姿态的变化以及大气紊流等因素都将直接导致光电载荷平台的视轴指向不稳定,而平台工作过程中的启动、制动都要求其超调量尽量不超过目标值的20%^[1],因而平台需要较强的抗扰性,来提高平台的视轴稳定精度 ...

2015

0.0

. 2015, 23(8):2296-2305

ADRC control system for airborne opto-electronic platform

航空光电稳定平台的自抗扰控制系统

Wei Wei , Dai Ming , Li Jia-quan

魏伟, 戴明, 李嘉全

... 目前国内外的航空光电稳定平台主要采用传统电流反馈、速度反馈、位置反馈的三闭环控制模式^[2],没有从根本上,即从力矩作用角度对扰动进行衰减 ...

2007

0.0

. 2007, 15(4):458-463

Review on angular accelerometer development

角加速度计发展综述

Wu Xiao-sheng , Chen Wen-yuan.

吴校生, 陈文元

... 一些利用加速度反馈的平台大都利用差分陀螺速度或直接用线加速度计组合的方式来获取加速度,以达到直接衰减扰动力矩的目的,但是差分陀螺速度所获得加速度信号受噪声的影响相对较大,而高精度加速度计造价昂贵^[3],一些小型平台负担不起这样的成本 ...

2015

0.0

. 2015, 45(1):202-208 DOI:doi:10.13229/j.cnki.jdxbgxb201501030

Improve isolation degree based on adaptive active disturbance rejection controller

基于自适应的自抗扰控制技术提高扰动隔离度

Li Xian-tao , Zhang bao, Zhao Chun-lei

李贤涛, 张葆, 赵春蕾

In order to further improve the isolation degree of disturbance of traditional controller, a new active disturbance-rejection controller based on frequency adaptation of disturbance is proposed. It is verified in the linear inverted pendulum system. The results show that the controller can avoid phase lag when extended state observer observes the disturbance with the high-order form. It can also at least reduce the disturbance error by 7.85 dB compared with the state feedback controller when the perturbation frequency is between 0 Hz and 2 Hz. The proposed controller has strong robustness, allowing the range of system parameters to change within 15%.

针对扩张状态观测器对二阶及二阶以上系统的扰动观测值存在相位滞后的问题，提出了一种基于扰动频率自适应的自抗扰控制的新方法，并在直线型倒立摆装置中进行了实验验证。实验结果表明:本文方法解决了扩张状态观测器对二阶及二阶以上系统的扰动观测值存在相位滞后的问题;在2 Hz以内随机扰动的作用下，对比传统状态反馈控制器，它将扰动隔离度至少提高了7.85 dB，同时，自抗扰控制器具有很强的鲁棒性，允许被控对象参数在15%的范围内浮动。

... 1 加入加速度反馈的优势传统航空光电稳定平台采用电流反馈、速度反馈、位置反馈的三闭环控制模式,其中电流反馈的目的主要是为了给外环带来足够的相位裕度,提高系统的响应速度,同时使得电机不再受到电子噪声即反电动势的影响,从而使得力矩和电机呈线性关系^[4] ...

2017

0.0

. 2017, 25(5):1281-1290

Feedforward compensation of mass unbalance moment for airborne photoelectric stabilized platform

航空光电稳定平台质量不平衡力矩的前馈补偿

Shen Shuai , Zhang Bao , Li Xian-tao

申帅, 张葆, 李贤涛

The effect of mass unbalanced moment under high-frequency vibration of a helicopter on the performance of a photoelectrical stabilized platform was discussed. A system model based feedforward compensation method for mass unbalanced moment was proposed on the basis of a three closed-loop control system with current feedback, velocity feedback and position feedback on the traditional photoelectrical stabilized platform. By calibrating the mass eccentricity of the platform, the acceleration signals of the platform were obtained by a acceleration sensor to perform the feedforward compensation to suppress the mass unbalanced moment of the platform. The experiment results show that the disturbance isolation increases at least 6.4 dB after inducing the feedforward compensation system as compared with that of the traditional three closed-loop control system. Moreover, as compared with that of compensation scheme using a disturbance observer, the proposed photoelectrical stabilized platform system with the feedforward compensation not only increases its compensation ability about 12.9 dB at low-frequency, but also overcomes the problems that disturbance observer can not compensate mass unbalanced moment at high-frequency. It increases greatly the disturbance isolation at full frequencies, allows the visual axis to better keep in an inertial space and shows high practical values.

... 电流反馈的引入实际上使电机在加速度反馈环节内变成一个理想的比例环节,而如果没有加速度反馈环节,则电流环会使电机在速度环内变成一个理想的积分环节^[5] ...

1994

0.0

... 在这里加速度闭环采用高增益控制方法^[6,7],则系统特征方程为: ...

2006

0.0

... 在这里加速度闭环采用高增益控制方法^[6,7],则系统特征方程为: ...

2007

0.0

. 2007, 1(1):24-31 DOI:doi:10.3969/j.issn.1673-8128.2007.01.004

Active disturbance rejection control technique

自抗扰控制技术

Han Jing-qing.

韩京清

摘　要：本文提出了解决控制问题的新思路:"解决控制问题是在系统运行过程中施加控制力来达到控制目的的过程的控制"的思想;介绍了如何从"发扬经典PID技术的精髓,吸取现代控制理论成果,开发利用非线性特性,通过计算机平台上的仿真研究"中产生自抗扰控制技术的全过程:并介绍组成自抗扰控制技术主要子技术:跟踪微分器、扩张状态观测器、非线性反馈效应和几个有用的非线性函数.

... 韩京清教授^[8]于1994年,提出了非线性跟踪微分器的全新理论 ...

... (1)开关型跟踪微分器^[8] ...

1994

0.0

. 1994, 14(2):177-183

Nonlinear tracking-differentiator

非线性跟踪-微分器

Han Jing-qing , Wang Wei.

韩京清, 王伟

... 跟踪微分器的工作流程^[9]:输入信号 v(t)经过跟踪微分器后将输出两个信号 z1和 z2,其中 z1跟踪 v(t),z2=z·1,从而把 z2作为 v(t)的#cod#x0201c ...

2003

0.0

. 2003, 20(6):875-878

Nonlinear tracking-differentiator with high speed in whole course

全程快速非线性跟踪-微分器

Wang Xin-hua , Chen Zeng-qiang , Yuan Zhu-zhi.

王新华, 陈增强, 袁著祉

... (2)快速非线性跟踪微分器^[10] ...

2006

0.0

... (3)离散线性跟踪微分器^[11] ...

1999

0.0

... (4)离散最速型跟踪微分器^[12] ...

2014

0.0

... 如果在跟踪微分器的开关线附近,加大线性区的宽度可以有效地减小系统震荡,而且根据线性区边界形状的不同,跟踪微分器所表现出的性能也会有很大的不同^[13,14] ...

2009

0.0

. 2009, 27(4):435-440

Construction of augmented proportion navigation law with tracking differentiator

利用跟踪-微分器构造增广比例导引律

Peng Jian-liang , Sun Xiu-xia , Dong Wen-han

彭建亮, 孙秀霞, 董文瀚

Engineering College, Air Force Engineering University, Xi’an 710038, China

A new approach of constructing augmented proportion navigation (APN) is investigated. Light of sight (LOS) angle velocity and acceleration are estimated using a tracking differentiator (TD) with filtering function. A coupler is constructed with a delay section and command softening sector to eliminate the bad effects of TD’s transient process on guidance performance. Some typical applications of TDs are given. A new terse fast TD without chattering is designed based on the merits and drawbacks of typical TDs. Simulation results show that APN with TD has good guidance performance, and is simple to implement.

研究了一种构造增广比例导引律的方法. 采用具有较强滤波功能的跟踪–微分器来估计视线角速度和视线角加速度，并将信号延迟环节和指令“软化”环节构成导引耦合器来消除跟踪–微分器过渡过程对导引性能的不利影响. 给出了几种典型跟踪–微分器构造增广比例律时的应用方法，针对典型跟踪–微分器的优缺点，提出了一种简洁快速无振荡跟踪–微分器，并将其用于增广比例导引. 仿真实验表明，具有跟踪–微分器结构的增广比例导引方案有良好的导引性能，且简单可行.