作者简介:邵克勇(1970-),男,教授,博士.研究方向:鲁棒控制,智能控制.E-mail:1127073951@qq.com
针对一类无平衡点的分数阶混沌系统,首先通过分数阶微分变换方法(FDTM)得到它的解序列。然后,研究了系统的Kaplan-Yorke维数和耗散性,基于系统的离散映射通过QR分解得到最大Lyapunov特征指数,通过该特征指数可以判断系统是否保持混沌。最后,给出一种全状态自适应控制方法,使系统的状态变量追踪期望轨迹,并通过数值模拟验证了本文算法的可行性。
For a class of chaotic system without equilibrium point, its solution series is obtained by the Fractional Differential Transformation Method (FDTM). Then, the Kaplan-Yorke dimension and the dissipativity of the system are investigated. The Lyapunov characteristic exponents are calculated based on the discrete map of the system through QR factorization algorithm, and the largest Lyapunov characteristic exponent is applied to judge whether the system keeps chaos or not. Finally, a full state based adaptive controller for the fractional order chaotic system is designed, which allows the states of the system to track the desired constant. The feasibility of the proposed algorithm is verified by numerical simulation.
分数阶系统是包含分数阶积分与微分的动态系统, 它可以有效地应用于物理系统建模[1, 2, 3]。在整数阶微积分的意义下, Poincare-Bendixon定理指出:连续自治系统出现混沌现象的微分阶次必须大于等于3[4, 5]。但是, 人们在研究中发现, 在分数阶微积分的意义下, 在许多阶次低于3的分数阶非线性系统中, 仍然存在混沌现象[6]。由于分数阶混沌系统相比于整数阶具有更好的发展前景, 它的理论研究及实际应用受到国内外学者的普遍关注。然而该领域内的研究成果仍然偏少, 其中一个主要原因是分析非线性分数阶系统稳定性的理论工具具有局限性。文献[7]提出了基于线性分数阶系统稳定性理论的混沌控制方法, 然而这种方法只验证了局部的稳定性。文献[8]提出了主动控制的方法, 这种方法利用非线性控制律来消除控制系统中的非线性项, 再根据线性分数阶系统稳定性理论, 设计一个线性控制律来稳定此系统, 但当系统中的参数未知时, 不能用主动控制方法来设计控制器。文献[9]研究了一类整数阶新型金融系统的自适应控制。文献[10, 11]研究了分数阶混沌系统的自适应控制, 其中控制变量存在于局部系统方程中。
本文针对一类无平衡点的分数阶混沌系统, 设计了一种全状态自适应控制器, 在不消除非线性项的情况下来追踪期望轨迹。最后通过数值模拟, 验证了该算法的可行性。
本节给出了分数阶微积分和微分变换方法的一些定义和性质[12]。
Riemann-Liouville定义[13], 表示如下:
式中:
根据方程(1)(2), 分数阶微分和积分算子的阶次为
由此, 可以得到
选择Caputo求解分数阶微分方程的重要原因是它对常数求导结果为0, 然而Riemann-Liouville分数阶微分对常数求导结果不恒为0。
函数
式中:
式中: 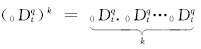
近似函数
以下是Caputo分数阶微分变换的基本性质[14]:①如果f(t)=g(t)± h(t), 则F(k)=g(k)± H(k); ②如果f(t)=g(t)h(t), 则F(k)=
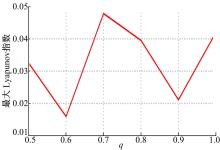
对于分数阶系统来说, 最常用的方法是用时间序列重构相空间, 计算最大Lyapunov指数[15], 这种做法仍有很多缺点, 如难以选择嵌入维数以及相空间重构的固有延迟参数[16]。本文利用FDTM得到一组分数阶微分方程的解, 用于计算分数阶系统中的Lyapunov特征指数。
引理1[17] 设
式中:
假设存在一个Lyapunov函数
式中:
提出一个分数阶系统方程:
式中:
2.1.1 平衡点
由于系统方程(9)在
2.1.2 分数阶Lyapunov维数和耗散性
选择参数:c1=1; c2=1; c3=1; c4=0.75; q=0.95。这个系统的差分变换为:
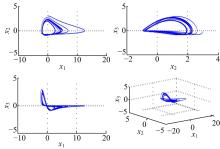
选取时间间隔Δ t=0.01、N=4, 混沌吸引子的相图如图1所示。
利用文献[20]中提到的方法, 令L1=0.012, L2=-0.0124, L3=-3.6386, L1+L2+L3=-3.6390< 0。根据Kaplan Yorke猜想, 定义系统(9)的分数阶Lyapunov维数[21]如下:
式中:
受控的分数阶混沌系统为:
式中:
假设:
式中:
研究了使得系统的状态x1 、x2 、x3 达到常数r1 、r2 、r3 的控制器u1 (x)、u2 (x)、u3 (x)设计问题。
设控制误差为:
则动态误差为:
式中:
为了简便, 假设
定理2 设计一个自适应控制器为:
式中:
如果满足以下条件:
则系统(12)是渐近稳定的。
证明 误差动态方程为:
参数估计误差定义为
根据分数阶的性质, 可以得到:
因此, 构造Lyapunov函数为:
根据引理1, 得:
由式(19)和(20)可以得到:
根据定理1, 可得系统(12)渐近稳定。
需要指出的是, 在本文方法中, 控制器包含所有状态信息, 它使控制器更加灵活。
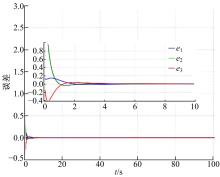
对于含有不确定参数ci 的系统(12), (i=1, 2, 3, 4), q=0.95, r1=r2=r3=0, 并且:
其中, 初始状态
当
本文设计了一种自适应控制器, 使系统状态变量追踪期望轨迹, 但追踪变量轨迹仍有待研究。
研究了一类无平衡点的混沌系统, 通过FDTM得到它的解集, 并分析了该系统的特点。通过判断最大Lyapunov特征指数, 给出了保持系统混沌的阶次范围。针对分数阶混沌系统设计出一种全状态自适应控制器, 可以用于追踪期望轨迹。最后, 通过数值模拟验证了本文方法的可行性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|