OPRA方向关系网络的时空推理

引用本文

王生生, 王创峰, 谷方明. OPRA方向关系网络的时空推理. 2017, 47(4): 1238-1243
WANG Sheng-sheng, WANG Chuang-feng, GU Fang-ming. Spatio-temporal reasoning for OPRA direction relation network. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1238-1243 复制到剪切板

Permissions

OPRA方向关系网络的时空推理

王生生¹, 王创峰², 谷方明¹

1.吉林大学计算机科学与技术学院,长春 130012

2.吉林大学软件学院,长春 130012

通讯作者：谷方明(1978-),男,讲师,博士.研究方向:人工智能.E-mail:gufm@jlu.edu.cn

作者简介:王生生(1974-),男,教授,博士生导师.研究方向:机器视觉,时空推理.E-mail:wss@jlu.edu.cn

基金:国家自然科学基金项目(61472161,61133011,61402195,61502198,61303132,61202308); 吉林省科技发展计划项目(20140101201JC).

摘要

由于目前的有向点方向代数(OPRA)推理只关注3个空间对象的静态关系推理,本文针对n个对象的方向关系定义了OPRA方向关系网络的时空推理问题。基于约束传播和概念领域理论,利用OPRA关系之间的空间约束和时间演变规律,给出了OPRA方向关系网络时空推理算法,解决了n个对象间动态OPRA关系的推理问题。本文算法可以应用于机器人导航、无人机导航、舰艇导航、战场分析等领域。

关键词: 人工智能; 时空推理; 有向点关系代数; 约束传播; 概念邻域

中图分类号:TP18 文献标志码:A 文章编号:1671-5497(2017)04-1238-06

Spatio-temporal reasoning for OPRA direction relation network

WANG Sheng-sheng¹, WANG Chuang-feng², GU Fang-ming¹

1.College of Computer Science and Technology, Jilin University, Changchun 130012, China

2.College of Software, Jilin University, Changchun 130012, China

Abstract

Oriented Point Algebra (OPRA) is one of hot topics in qualitative spatial reasoning. Previous researches were mainly focused on spatial reasoning with at most three static objects. However, many scenarios involve more objects and the scenarios may be dynamic. To deal with these problems, the spatio-temporal reasoning of OPRA direction relation network is defined, which is a dynamic reasoning framework for large number of objects. The constraint propagation theory is used to handle the problem of large number, and the conceptual neighborhoods theory is used to handle the dynamic reasoning. An algorithm is proposed to fuse the two issues, which is a solution for the OPRA reasoning problem of n dynamic objects. The method can used in robot navigation, unmanned aerial vehicle navigation, ship navigation and battlefield analysis and so on.

Keyword: artificial intelligence; spatio-temporal reasoning; oriented point relation algebra(OPRA); constraint propagation; conceptual neighborhoods

Show Figures

0 引言

定性空间推理是人工智能的重要组成部分^{[1, 2, 3, 4]}, 在基于内容的图像检索^[5]、生物信息^[6]、地理信息系统(GIS)^[7]、机器人^[8]、空间数据库^[9]等领域有广泛的应用。方向关系推理是空间推理的一个重要方面^{[10, 11]}。有向点关系代数(Oriented point relation algebra, OPRA)是著名的基于点对象(Point-based)的方向关系模型^[4]。它把空间对象建模为带方向的点, 称为有向点。通过两个有向点之间的连线与有向点自身方向之间的夹角来表示方向关系。

OPRA方向关系推理在GIS、无线传感器网络、机器人导航等领域都有着重要应用意义^{[7, 12]}, 但也是人工智能领域比较困难的问题之一^[11]。2012年, Mossakowski等^[13]研究了OPRA方向关系的复合运算。2014年, Wang等^[14]研究了OPRA方向关系的多粒度复合推理, 使得OPRA推理可以应用于任意混合粒度之间。上述工作只涉及了3个空间对象之间的静态OPRA方向关系。

在实际应用中, 场景是动态变化的, 涉及的空间对象也是众多的。关于多空间对象的、动态的OPRA方向关系推理鲜有报道, 本文称这一主题为OPRA方向关系网络时空推理。OPRA网络时空推理在机器人导航、无人机导航、舰艇导航、战场分析等领域有广阔的应用前景。

本文应用约束传播^[15]思想解决 $\begin{matrix} n \end{matrix}$ 个对象单一时刻OPRA方向关系推理问题; 通过概念邻域理论^[16]解决多时刻OPRA方向关系推理。然后融合这两种方法, 提出OPRA方向关系网络时空推理算法, 它可以处理多时刻、多对象间的OPRA方向关系推理问题。

1 OPRA理论

为便于理解, 在给出OPRA方向关系网络时空推理的定义之前先给出OPRA理论的几个基本概念。然后将依次给出OPRA方向关系网络的空间、时间和时空推理算法。

1.1 OPRA概述

OPRA将对象建模为无大小、有方向的点。这样的模型可以方便地对应于有方向的或运动的物体。

定义1 有向点(o-point)

有向点有两个基本属性:位置和方向。一个有向点 $\begin{matrix} S \end{matrix}$ 记为:

$\begin{matrix} S = (P_{S}, ϕ_{S}) (1) \end{matrix}$

式中: $\begin{matrix} P_{S} \end{matrix}$ 表示点的位置, 用该点的坐标表示, 即 $\begin{matrix} P_{S} = (x_{S}, y_{S}); ϕ_{S} \end{matrix}$ 表示点的方向, 用取值于[0, 2π )的角度表示, 这是从 $\begin{matrix} x \end{matrix}$ 轴正方向旋转到 $\begin{matrix} S \end{matrix}$ 的方向所成的旋转角, 并认为该旋转角取值区间是[0, 2π )上的循环群, 例如, 认为-π /3等于5π /3。

定义2 OPRA关系(OPRA_m)

给定粒度参数m(m是一个正整数), 对于有向点A、B, 它们的OPRA关系OPRA_m(A, B)定义为:

$\begin{matrix} \begin{matrix} OPR A_{m} (A, B) = \\ \{\begin{matrix} ∠_{i}^{j}, |\begin{matrix} i = Q_{m} (φ_{AB} - ϕ_{A}) \\ j = Q_{m} (φ_{BA} - ϕ_{B}) \end{matrix}, if P_{A} \neq P_{B} \\ ∠ k, |k = Q_{m} (γ = ϕ_{B} - ϕ_{A}), if P_{A} = P_{B} \end{matrix} (2) \end{matrix} \end{matrix}$

式中:φ _AB=atan2(y_B-y_A, x_B-x_A), atan2(y, x)是从x轴正向到向量(x, y)所成的旋转角, 规定其取值范围为[0, 2π )。Q_m(δ )是一个粒度化操作, 把一个定量的角度映射为定性标号, 定义为:

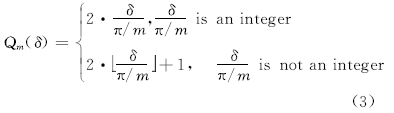
这里, 规定所有标号(即式(2)中的i、j、k, 或者说Q_m(δ )的值)都定义在4m的循环群上。每一个OPRA_m (A, B)的取值称为一个基本OPRA关系。对给定的m, 基本OPRA关系的取值集合称为OPRA_m关系全集, 记为 $\begin{matrix} U_{m}^{OPRA} 。 \end{matrix}$ 图1、图2是两个OPRA₃的例子。显然, 如果OPRA_m (A, B)= $∠_{i}^{j}$ , 则OPRA_m(B, A)= $∠_{j}^{i}$ , 如果OPRA_m (A, B)=∠k, 则OPRA_m (B, A)=∠(-k)。即OPRA逆关系具有这样的计算规则:

$\begin{matrix} ~ ∠_{i}^{j} = ∠_{j}^{i}, ~∠ k = ∠ (- k) (4) \end{matrix}$

	Figure Option View Download New Window
	图1 OPRA₃(A, B)= $\begin{matrix} ∠_{4}^{9} \end{matrix}$ Fig.1 OPRA₃(A, B)= $\begin{matrix} ∠_{4}^{9} \end{matrix}$

定义3 OPRA复合运算

对于OPRA_m的基本关系r₁、r₂它们的复合运算定义为:

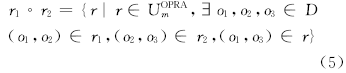
式中:D是有向点的集合。OPRA复合运算是弱复合, 证明参见文献^[13]。

	Figure Option View Download New Window
	图2 OPRA₃(A, B)=∠5Fig.2 OPRA₃(A, B)=∠5

2012年, Mossakowski^[13]用3个约束(turn, sign, triangle)给出了判定OPRA复合表项的方法, 并给出了完整的证明。通过该方法可以构造出OPRA复合表, 进而通过查表完成OPRA复合运算。

1.2 OPRA网络时空推理

OPRA方向关系网络是为了建模任意多个(数量固定)对象之间的方向关系。

定义4 OPRA关系网络

给定粒度参数m, 对于n个有向点P₁, P₂, …, P_n 构成的集合D, 在时刻t, D上的OPRA关系网络定义为 $\begin{matrix} n \times n \end{matrix}$ 的矩阵:

$\begin{matrix} Θ_{D}^{t} = [\begin{matrix} R_{1, 1}^{t} & R_{1, 2}^{t} & \dots & R_{1, n}^{t} \\ R_{2, 1}^{t} & R_{2, 2}^{t} & \dots & R_{2, n}^{t} \\ : & : & : \\ R_{n, 1}^{t} & R_{n, 2}^{t} & \dots & R_{n, n}^{t} \end{matrix}] (6) \end{matrix}$

式中: $\begin{matrix} R_{i, j}^{t} \end{matrix}$ 是已确知的 $\begin{matrix} OPR A_{m} (P_{i}, P_{j}) \end{matrix}$ 的取值集合。例如, 如果已确知 $\begin{matrix} OPR A_{m} (P_{i}, P_{j}) = ∠_{1}^{2}, \end{matrix}$ 则 $\begin{matrix} R_{i, j}^{t} = {∠_{1}^{2}}; \end{matrix}$ 如果完全不知道 $\begin{matrix} OPR A_{m} (P_{i}, P_{j}) \end{matrix}$ 的取值, 则认为 $\begin{matrix} R_{i, j}^{t} = U_{m}^{OPRA}, \end{matrix}$ 即可能取任意可能的取值; 如果确知 $\begin{matrix} OPR A_{m} (P_{i}, P_{j}) \end{matrix}$ 只可能在某些OPRA关系中取值, 则 $\begin{matrix} R_{i, j}^{t} \end{matrix}$ 即为这些取值构成的集合。对一个精确化了的 $\begin{matrix} Θ_{D}^{t}, 显然有 R_{i, i}^{t} = {∠ 0}, R_{i, j}^{t} = ~ R_{j, i}^{t}, ~ R_{j, i}^{t} \end{matrix}$ 表示对 $\begin{matrix} R_{i, j}^{t} \end{matrix}$ 中每一个关系取逆的结果集合。这两个性质可以加速 $\begin{matrix} Θ_{D}^{t} \end{matrix}$ 的精确化过程。OPRA方向关系网络简称OPRA网络, 下文同。

OPRA网络的空间、时间、时空推理致力于确定OPRA网络或网络序列中的未知元素。

定义5 OPRA方向关系网络的空间推理

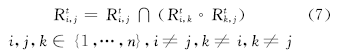
对于由n个有向点构成的集合D, 在时刻t有OPRA关系网络 $\begin{matrix} Θ_{D}^{t} 。 \end{matrix}$ 对 $\begin{matrix} Θ_{D}^{t} \end{matrix}$ 中的元素应用规则如下:

直到所有 $\begin{matrix} R_{i, j}^{t} (i, j \in {1, 2, \dots, n}, i \neq j) \end{matrix}$ 不再变化为止。这一得到新 $\begin{matrix} Θ_{D}^{t} \end{matrix}$ 的过程称为对OPRA关系网络 $\begin{matrix} Θ_{D}^{t} \end{matrix}$ 的空间推理。

使用概念邻域进行时间维度上的推理由来已久。概念邻域由Freksa^[17]于1992年为解决事件的时间关系而提出。2007年, Dylla等^[16]研究了OPRA的概念邻域。

定义6 OPRA概念邻域

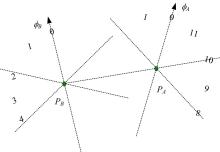
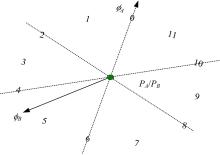
有向点A、B做连续运动, 给定粒度参数m, 在时刻t有OPRA_m(A, B)=r。在时刻t', 有OPRA_m(A, B)=r'(r'与r可能相同), 如果|t'-t|足够小, 以至于在时间段[t', t]或[t, t']内, OPRA_m(A, B)无法取得r与r'之外的其他值, 则称r'是r的邻域, r'的取值集合称为r的概念邻域。r的概念邻域记作adj(r)。

在实际应用中, 由于物理因素, 两个物体位置重合的情况很难遇到, 这意味着在OPRA关系中, 形式 $\begin{matrix} ∠ i \end{matrix}$ 比较罕见。为此, 本文仅讨论位置不重合的OPRA关系, 即具有形式 $\begin{matrix} ∠_{i}^{j} \end{matrix}$ 的情况。显然, OPRA的概念邻域具有如下计算规则:

$\begin{matrix} \begin{matrix} adj (∠_{i}^{j}) = {∠_{i - 1}^{j - 1}, ∠_{i - 1}^{j}, ∠_{i - 1}^{j + 1}, ∠_{i}^{j - 1}, \\ ∠_{i}^{j}, ∠_{i}^{j + 1}, ∠_{i + 1}^{j - 1}, ∠_{i + 1}^{j}, ∠_{i + 1}^{j + 1}} (8) \end{matrix} \end{matrix}$

定义7 OPRA方向关系网络时间推理

在时间序列 $\begin{matrix} t_{1}, t_{2}, \dots, t_{s} \end{matrix}$ 上, 有OPRA网络 $\begin{matrix} Θ_{_{D}}^{t_{1}}, Θ_{_{D}}^{t_{2}}, \dots, Θ_{_{D}}^{t_{s}}, \end{matrix}$ 如果o-point集合 $\begin{matrix} D \end{matrix}$ 中的有向点做连续运动, 对 $\begin{matrix} Θ_{_{D}}^{t_{1}}, Θ_{_{D}}^{t_{2}}, \dots, Θ_{_{D}}^{t_{s}} \end{matrix}$ 应用如下规则:

$R_{i, j}^{t_{u + 1}} = R_{i, j}^{t_{u + 1}} ⋂ adj (R_{i, j}^{t_{u}}), u \in {t_{1}, t_{2}, \dots, t_{s - 1}} (9)$

$\begin{matrix} \begin{matrix} R_{i, j}^{t_{v - 1}} = R_{i, j}^{t_{v - 1}} ⋂ adj (R_{i, j}^{t_{v}}), v \in {t_{2}, t_{3}, \dots, t_{s}} (10) \end{matrix} \end{matrix}$

直到所有 $\begin{matrix} R_{i, j}^{t} (t \in {t_{1}, t_{2}, \dots, t_{s}}, i, j \in {1, 2, \dots, n}) \end{matrix}$ 不再变化为止。这一计算新 $\begin{matrix} Θ_{_{D}}^{t_{1}}, Θ_{_{D}}^{t_{2}}, \dots, Θ_{_{D}}^{t_{s}} \end{matrix}$ 的过程称为对OPRA网络 $\begin{matrix} Θ_{_{D}}^{t_{1}}, Θ_{_{D}}^{t_{2}}, \dots, Θ_{_{D}}^{t_{s}} \end{matrix}$ 的时间推理。

定义8 OPRA方向关系网络的时空推理

在时间序列 $\begin{matrix} t_{1}, t_{2}, \dots, t_{s} \end{matrix}$ 上, 有OPRA网络 $\begin{matrix} Θ_{_{D}}^{t_{1}}, Θ_{_{D}}^{t_{2}}, \dots, Θ_{_{D}}^{t_{s}}, \end{matrix}$ 如果o-point集合D中的有向点做连续运动, 对 $\begin{matrix} D Θ_{_{D}}^{t_{1}}, Θ_{_{D}}^{t_{2}}, \dots, Θ_{_{D}}^{t_{s}} \end{matrix}$ 应用如下规则:

OPRA网络时空推理可以应用于众多领域, 下面举例说明。在某复杂环境中, 有多个对象协同执行任务。例如, 在海上多艘渔船协同捕鱼或多艘打捞船协同作业; 在战场上, 多辆战车协同作战; 在室内, 多个智能机器人协同执行任务。在环境复杂且具有严重干扰的情况下, 难以实现空间对象的精确定位。而OPRA方向关系虽然表达简单, 但容易获得, 并且语义丰富, 非常适合在这些情况下做空间建模。然而, 由于视线或电磁波被障碍物、烟雾或人为干扰等因素阻碍, 部分对象间的OPRA方向关系在某些时刻也无法直接获得。在这种情况下, 可以应用OPRA网络时空推理算法推断出缺失的OPRA方向关系, 从而降低所采集历史信息中的不确定性, 以便于后续智能决策。

2 OPRA方向关系网络空间推理算法

OPRA方向关系网络空间推理(简称OPRA网络空间推理)可以在一个时刻上, 利用多个对象间的OPRA关系进行推理, 从而降低未知关系的不确定性。约束传播是空间推理领域被广泛讨论的主题, 它利用一系列巧妙安排的复合推理, 把对象之间隐含的约束尽可能地发掘出来, 这些发掘出来的隐含约束事实上提供了未知关系的信息。这一节借鉴约束传播理论, 给出OPRA网络空间推理的算法实现。

算法:OPRA-NET-SPATIAL-REASON

输入:OPRA网络Θ _D。o-point对象是x₁, x₂, …, x_n, R_{i, j}是(x_i, x_j)之间的OPRA关系。

输出:如果检测到Θ _D中的关系存在矛盾, 输出fail; 否则, 输出精化后的关系网络Θ _D。

Q¬ { (i, j)|i< j };

while Q¹ Ø do{

select and delete an pair (i, j) from Q;

for k¹ i, k¹ j (kÎ {1, 2, …, n}) do{

if REVISION(i, j, k) then

if R_{i, j}=Ø then return fail;

else if (i, j) (not in) Q add (i, j) to Q;

if REVISION(k, i, j) then

if R_{k, i}=Ø then return fail;

else if (k, i) (not in) Q add (k, i) to Q.

}

REVISION(i, j, k){

t:=R_{i, j};

R_{i, j}:=R_{i, j}∩ (R_{i, k}º R_{k, j});

if (t = R_{i, j}) then return false;

R_{j, i}:=Converse(R_{i, j});

return true;

}

上述算法中, Q是容器, 例如可以是FIFO(先进先出)队列; 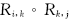是OPRA复合运算; Converse(R_{i, j})是R_{i, j}的逆。

下面分析该算法需要的复合运算的上界。对于给定的粒度参数 $\begin{matrix} m, \end{matrix}$ OPRA基本关系数是有限的, 为4m× (4m+1)。因此, 任意R_{i, j} 必收敛于某个 $\begin{matrix} U_{m}^{OPRA} \end{matrix}$ 的子集, 从而整个算法是收敛的。考虑最坏情况, 每个 $\begin{matrix} R_{i, j} \end{matrix}$ 每次执行REVISION只会约去一个基本OPRA关系, 而它最多可能有4m× (4m+1)个关系。Θ _D 共有n× n个R_{i, j}, 每次REVISION需要一次复合操作, 故该算法具有时间复杂度 $\begin{matrix} O (n^{2} m^{2}), \end{matrix}$ 这里以复合运算的次数计算。

3 OPRA方向关系网络时间推理算法

OPRA方向关系网络时间推理(简称OPRA网络时间推理)在时间维度上将未知的关系精确化。这一部分将给出通过概念邻域进行OPRA关系网络时间推理的算法。

算法:OPRA-NET-TIME-REASON

输入:在时间序列t₁, t₂, …, t_s上的OPRA网络序列 $\begin{matrix} Θ_{_{D}}^{^{t_{1}}} \end{matrix}$ , $\begin{matrix} Θ_{_{D}}^{^{t_{2}}} \end{matrix}$ , …, $\begin{matrix} Θ_{_{D}}^{^{t_{s}}} \end{matrix}$ 。D={x₁, x₂, …, x_n}是o-point集合, $\begin{matrix} R_{i, j}^{t} \end{matrix}$ 是 $\begin{matrix} Θ_{D}^{t} \end{matrix}$ 的i行j列的元素, 表示(x_i, x_j)在时刻t的OPRA关系。

输出:预测的关系网络序列 $\begin{matrix} Θ_{D}^{t_{1}} \end{matrix}$ , $\begin{matrix} Θ_{D}^{t_{2}} \end{matrix}$ , …, $\begin{matrix} Θ_{D}^{t_{s}} \end{matrix}$ 。

for v=2 to s do{

for every $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ in $\begin{matrix} Θ_{D}^{t_{v}} \end{matrix}$ do{

$\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ = $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ ∩ adj( $\begin{matrix} R_{i, j}^{t_{v - 1}} \end{matrix}$ )

}

for v=s-1 to 1 by -1 do{

for every $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ in $\begin{matrix} Θ_{D}^{t_{v}} \end{matrix}$ do{

$\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ = $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ ∩ adj( $\begin{matrix} R_{i, j}^{t_{v + 1}} \end{matrix}$ )

}

4 本文算法

OPRA网络空间推理考虑了关系之间的制约因素, 却没有处理关系在时间维度上的演变现象。OPRA网络时间推理算法考虑了关系在时间维度上的演变规律, 却忽略了关系之间的制约规则。融合二者, 可以得到一个兼具双方优势的算法, 即OPRA方向关系网络时空推理算法。该算法可以大大提升OPRA网络序列中未知关系的确定性。

算法:OPRA-NET-SPATIO-TEMPORAL-REASON

输入:在时间序列t₁, t₂, …, t_s上的OPRA网络序列 $\begin{matrix} Θ_{_{D}}^{t_{1}} \end{matrix}$ , $\begin{matrix} Θ_{_{D}}^{t_{2}} \end{matrix}$ , …, $\begin{matrix} Θ_{_{D}}^{t_{s}} \end{matrix}$ 。D={x₁, x₂, …, x_n}是o-point集合, $\begin{matrix} R_{i, j}^{t} \end{matrix}$ 是 $\begin{matrix} Θ_{D}^{t} \end{matrix}$ 的i行j列的元素, 表示(x_i, x_j)在时刻t的OPRA关系。

输出:如果检测到 $\begin{matrix} Θ_{_{D}}^{t_{1}} \end{matrix}$ , $\begin{matrix} Θ_{_{D}}^{t_{2}} \end{matrix}$ , …, $\begin{matrix} Θ_{_{D}}^{t_{s}} \end{matrix}$ 中的关系存在矛盾, 输出fail; 否则输出预测的关系网络 $\begin{matrix} Θ_{_{D}}^{t_{1}} \end{matrix}$ , $\begin{matrix} Θ_{_{D}}^{t_{2}} \end{matrix}$ , …, $\begin{matrix} Θ_{_{D}}^{t_{s}} \end{matrix}$ 。

$\begin{matrix} Θ_{_{D}}^{t_{1}} \end{matrix}$ =OPRA-NET-SPATIAL-REASON( $\begin{matrix} Θ_{_{D}}^{t_{1}} \end{matrix}$ )

if $\begin{matrix} Θ_{_{D}}^{t_{1}} \end{matrix}$ =fail then return fail.

for v=2 to s do{

for every $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ in $\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ do{

$\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ = $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ ∩ adj( $\begin{matrix} R_{i, j}^{t_{v - 1}} \end{matrix}$ )

}

$\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ =OPRA-NET-SPATIAL-REASON( $\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ )

if $\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ =fail then return fail.

}

for v=s-1 to 1 by -1 do{

for every $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ in $\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ do{

$\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ = $\begin{matrix} R_{i, j}^{t_{v}} \end{matrix}$ ∩ adj( $\begin{matrix} R_{i, j}^{t_{v + 1}} \end{matrix}$ )

}

$\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ =OPRA-NET-SPATIAL-REASON( $\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ )

if $\begin{matrix} Θ_{_{D}}^{t_{v}} \end{matrix}$ =fail then return fail.

}

5 实验验证

通过模拟实验演示OPRA网络时空推理算法对提高系统方向关系的确定性的效果。

实验在运行于Windows8.1上的Matlab环境中进行。它模拟30个对象执行协同任务。对象做方向和速度(0~1之间的随机数)都随机变化的连续运动。对象之间的方向关系构成一个OPRA网络。在整个任务执行过程中, 所有采样时刻形成的OPRA网络构成一个OPRA网络序列。这里, 取12个连续的采样时刻。由于某些干扰因素, 这个序列中包含很多无法直接检测的方向关系。这里为方便起见, 设定当o-point距离大于场景边长的30%时, OPRA关系无法检测。其他的相关参数如下:粒度参数m=2, 场景范围为100× 100。

为最大程度地提高整个关系网络序列的确定性, 应用OPRA网络时空推理算法对这个关系网络序列进行精化。在时刻 $\begin{matrix} t, 对象 i 、 j \end{matrix}$ 之间的OPRA关系记为 $\begin{matrix} R_{i, j}^{t}, \end{matrix}$ 定义它的精确度为:

$\begin{matrix} d = 1 - (| R_{i, j}^{t} | - 1) / (4 m \times (4 m + 1) - 1) (14) \end{matrix}$

它保证当 $\begin{matrix} | R_{i, j}^{t} | = 1 \end{matrix}$ 时, 精确度为1, 当 $\begin{matrix} | R_{i, j}^{t} | = 4 m \times (4 m + 1) \end{matrix}$ 时, 精确度为0。对于OPRA网络 $\begin{matrix} Θ_{_{D}}^{t} \end{matrix}$ , 精确度d定义为所有 $\begin{matrix} R_{i, j}^{t} \end{matrix}$ 精确度的平均值。

在一次实验中, 进行OPRA网络时空推理, 各采样时刻的精确度如表1所示。表中, n_S是OPRA网络中的精确关系的数量, n_U是完全未知关系的数量, $\begin{matrix} d \end{matrix}$ 是关系网络的精确度。在10次试验中, 统计了整个网络序列的精确度平均值, 结果见表2。可以看到, 无论是单一时刻还是整个时间采样区间, 方向关系的精确度都得到了有效的提升。

表1 一次实验中OPRA网络时空推理之前、后的精确度 Table 1 Accuracy of OPRA relation net before and after OPRA net spatio-temporal reasoning in one experiment

表2 OPRA网络时空推理前后的精确度 Table 2 Accuracy of OPRA relation net before and after OPRA net spatio-temporal reasoning

6 结束语

定性空间推理是人工智能领域的主要研究方向之一, OPRA方向关系模型是近年定性空间推理的一个热点问题。然而, 此前对OPRA方向关系的推理问题研究仅限于复合推理, 它只能解决3个空间对象的静态关系推理问题。本文基于约束传播和概念领域理论, 提出了OPRA方向关系网络时空推理算法, 解决了 $\begin{matrix} n \end{matrix}$ 个空间对象、多时刻的推理问题。该算法可以应用于机器人导航、无人机导航、舰艇导航、战场分析等领域。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Duboisset M, Pinet F, Kang M A, et al. A general framework to implement topological relations on composite regions[C]//International Conference on Database and Expert Systems Applications, Berlin, 2007: 823-833. [本文引用:1]
[2]	Shen J, Wu M, Lv G, et al. Topological relationships calculation for 3D curves data set based on monotone chains[C]//The 18th International Conference on Geoinformatics, Beijing, China, 2010: 1-5. [本文引用:1]
[3]	Cohn A G. Qualitative spatial representation and reasoning techniques[C]//Annual Conference on Artificial Intelligence, Berlin, 1997: 1-30. [本文引用:1]
[4]	Moratz R. Representing relative direction as a binary relation of oriented points[C]//ECAI, 2006: 407-411. [本文引用:2]
[5]	Wang S, Liu D, Zhang C, et al. Representation, reasoning and similar matching for detailed topological relations with DTString[J]. Information Sciences, 2014, 276(1): 255-277. [本文引用:1]
[6]	Park S H, Ryu K H. Fast similarity search for protein 3D structure databases using spatial topological patterns[C]//International Conference on Database and Expert Systems Applications, Berlin, 2004: 771-780. [本文引用:1]
[7]	Vahidnia M H, Alesheikh A A, Alavipanah S K. A multi-agent architecture for geosimulation of moving agents[J]. Journal of Geographical Systems, 2015, 17(4): 353-390. [本文引用:2]
[8]	Cifuentes S, Girón-Sierra J M, Jiménez J. Virtual fields and behaviour blending for the coordinated navigation of robot teams: Some experimental results[J]. Expert Systems with Applications, 2015, 42(10): 4778-4796. [本文引用:1]
[9]	Batsakis S, Antoniou G, Tachmazidis I. Reasoning over Spatial Orientation Relations Using Rules[M]. Berlin: Springer, 2015: 123-134. [本文引用:1]
[10]	Chen J, Cohn A G, Liu D, et al. A survey of qualitative spatial representations[J]. The Knowledge Engineering Review, 2015, 30(1): 106-136. [本文引用:1]
[11]	Mossakowski T, Moratz R. Relations between spatial calculi about directions and orientations[J]. Journal of Artificial Intelligence Research, 2015, 54(1): 277-308. [本文引用:2]
[12]	欧阳继红, 祝东红, 富倩, 等. 基于 OPRA_ m的三维相对方位关系模型[J]. 吉林大学学报: 工学版, 2015, 45(5): 1535-1540. Ouyang Ji-hong, Zhu Dong-hong, Fu Qian, et al. Model for three-directional relative directions based on OPRA_ m[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(5): 1535-1540. [本文引用:1]
[13]	Mossakowski T, Moratz R. Qualitative reasoning about relative direction of oriented points[J]. Artificial Intelligence, 2012, 180(1): 34-45. [本文引用:3]
[14]	Wang S, Liu Y, Liu D, et al. Multi-granularity and metric spatial reasoning[J]. Expert Systems with Applications, 2014, 41(6): 3116-3133. [本文引用:1]
[15]	Li S, Liu W, Wang S. Qualitative constraint satisfaction problems: an extended framework with land marks[J]. Artificial Intelligence, 2013, 201(1): 32-58. [本文引用:1]
[16]	Dylla F, Wallgrün J O. Qualitative spatial reasoning with conceptual neighborhoods for agent control[J]. Journal of Intelligent and Robotic Systems, 2007, 48(1): 55-78. [本文引用:2]
[17]	Freksa C. Temporal reasoning based on semi-intervals[J]. Artificial Intelligence, 1992, 54(1/2): 199-227. [本文引用:1]

2007

0.0

... 0 引言定性空间推理是人工智能的重要组成部分^[1,2,3,4],在基于内容的图像检索^[5]、生物信息^[6]、地理信息系统(GIS)^[7]、机器人^[8]、空间数据库^[9]等领域有广泛的应用 ...

2010

0.0

1997

0.0

2006

0.0

... 有向点关系代数(Oriented point relation algebra,OPRA)是著名的基于点对象(Point-based)的方向关系模型^[4] ...

2014

0.0

2004

0.0

2015

0.0

... OPRA方向关系推理在GIS、无线传感器网络、机器人导航等领域都有着重要应用意义^[7,12],但也是人工智能领域比较困难的问题之一^[11] ...

2015

0.0

2015

0.0

2015

0.0

... 方向关系推理是空间推理的一个重要方面^[10,11] ...

2015

0.0

... 方向关系推理是空间推理的一个重要方面^[10,11] ...

... OPRA方向关系推理在GIS、无线传感器网络、机器人导航等领域都有着重要应用意义^[7,12],但也是人工智能领域比较困难的问题之一^[11] ...

2015

0.0

. 2015, 45(5):1535-1540 DOI:10.13229/j.cnki.jdxbgxb201505023

Model for three-directional relative directions based on OPRA_m

OPRA_ m 的三维相对方位关系模型

Ouyang Ji-hong , Zhu Dong-hong , Fu Qian

欧阳继红, 祝东红, 富倩, . 基于

1.College of Computer Science and Technology,Jilin University,Changchun 130012, China; 2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012,China

OPRA m is the classical model in the study of two-dimensional direction relationship. However, to solve practical problems, the multi-directional space relationship should be considered. In order to express the relative direction in three-dimensional space, the relative direction of the xoy plane is combined with the relative direction of the z -axis. A three-dimensional relative direction model, 3DOPRA m , is proposed by extending the model OPRA m for two-dimensional direction relationship, and two new relative angles are defined. Moreover, the formal definition of 3DOPRA m multi-granularity, its reverse relationship and the conceptual neighborhood of 3DOPRA m are given. Finally, the conceptual neighborhood based on the action of 3DOPRA m model is applied to describe the car navigation problems. Results show that, compared with existing two-dimensional model, the proposed model is more expressive and can describe more relative directions in three-dimensional space, which has great potential for practical applications.

OPRA m 是研究二维相对方位关系的经典模型之一,但解决实际问题通常需要考虑多维空间中的方位关系,为了表达三维空间中点对象间相对方位关系,将 xoy 平面相对方位和 z 轴相对方位相结合;通过定义与之相对应的能表达相对方位信息的两个相对角得到3DOPRA m 模型,并给出其在多粒度下的形式化定义及逆关系。给出了3DOPRA m 模型的概念邻域。最后用其基于动作的邻域关系描述汽车导航问题。结果表明,本文提出的模型能够细致、合理地表达三维空间中点对象间的相对方位关系,在实际中有广泛的应用前景。

... OPRA方向关系推理在GIS、无线传感器网络、机器人导航等领域都有着重要应用意义^[7,12],但也是人工智能领域比较困难的问题之一^[11] ...

2012

0.0

... 2012年,Mossakowski等^[13]研究了OPRA方向关系的复合运算 ...

... OPRA复合运算是弱复合,证明参见文献^[13] ...

... 2012年,Mossakowski^[13]用3个约束(turn,sign,triangle)给出了判定OPRA复合表项的方法,并给出了完整的证明 ...

2014

0.0

... 2014年,Wang等^[14]研究了OPRA方向关系的多粒度复合推理,使得OPRA推理可以应用于任意混合粒度之间 ...

2013

0.0

... 本文应用约束传播^[15]思想解决 n个对象单一时刻OPRA方向关系推理问题 ...

2007

0.0

... 通过概念邻域理论^[16]解决多时刻OPRA方向关系推理 ...

... 2007年,Dylla等^[16]研究了OPRA的概念邻域 ...

1992

0.0

... 概念邻域由Freksa^[17]于1992年为解决事件的时间关系而提出 ...