作者简介:周炳海(1965-),男,教授,博士生导师.研究方向:离散系统建模、调度与仿真.E-mail:bhzhou@tongji.edu.cn
针对混流装配线的准时化物料配送问题,综合考虑搬运设备的运载能力和装配线不允许缺货约束,构建了车辆装载与路径规划的联合优化模型。首先,进行了问题域的描述,并以最小化物料搬运期间所有工位中的最大加权库存水平为目标建立了数学规划模型。其次,结合该调度问题的两条基本性质,提出了回溯搜索算法以获得小规模问题的精确解。此外,为了有效地应对中大规模问题的爆炸搜索空间,构建了改进型离散人工蜂群算法。该算法通过在邻域变换中融入局部搜索和差分进化操作以提升其收敛性能。最后进行了仿真实验,结果验证了准时化配送模型及调度算法的可行性、有效性。
For Just-in-Time (JIT) part distribution problem in Mixed-Model Assembly Lines (MMALs), an integrated vehicle filling and routing scheduling model is presented with consideration of loading capacities and no sock-outs constraints of assembly lines. First, a scheduling problem domain is described and then the mathematical programming model is developed with an objective to minimize the maximum weighted inventory level in all stations and production cycles. Second, the backtracking method is established to optimally solve small-scale instances based on two properties of the proposed scheduling model. Third, a Modified Discrete Artificial Bee Colony (MDABC) algorithm is introduced to cope with the exploding search space of medium- and large-scale instances. Both local search and differential evolution operations are employed for neighbor search, which improves the convergence performance of the modified metaheuristic effectively. Finally, simulations are carried out and the experiment results verify the feasibility and effectiveness of the proposed JIT distribution model and methods.
随着产品多样化、客户化定制的不断发展, 混流装配模式已成为生产企业快速响应客户个性化需求的重要手段[1]。多种类型产品共线生产导致混装流水线所需物料的种类及其需求波动性显著增加, 而有限的线边库存容量使得准时化物料配送调度成为混流制造业面临的重大挑战。为此, 企业逐步采用基于超市系统的物料配送模式以保障装配线生产的顺畅运转[2]。该模式通过在作业车间设置多个物料超市以暂存和分拣来自中心仓库的物料, 并实现对临近工位多批次、小批量的准时化物料配送活动, 进而避免了占用大量的线边空间。据此可知, 进行混流装配线准时化物料配送问题的研究对提升企业的生产效率具有重要意义。
依据配送方式的不同, 混流装配线准时化物料配送研究大致分为循环配送(Milk-run delivery)和点对点配送(Point-to-point delivery)两类[3]。循环配送方式依据固定的行车线路, 利用Tow train等搬运设备对生产线子区段中各工位进行周期性补货; 点对点配送则利用AGV、Hoist搬运设备等对装配工位进行物料更新作业, 每次配送选择一个装配工位进行补货。近年来, 诸多国内外学者针对混流装配线的准时化物料配送调度问题行了较深入的研究[4, 5, 6, 7, 8]。这些文献大多针对循环配送方式的调度问题进行研究, 仅有文献[8]研究了点对点配送方式的准时化配送问题, 该模型考虑了Hoist的配送路径规划问题, 并未提及Hoist的装载问题。然而, 车辆装载问题与路径规划问题相互耦合, 共同构成了混装流水线准时化物料配送的重要环节, 不合理的车辆装载调度将导致装配线缺货或产生大量的线边库存, 这些都与准时化配送思想相违背。此外, 点对点配送问题与传统的AGV调度研究[9]、车辆路径问题(Vehicle routing problem, VRP)[10]及库存路径问题(Inventory routing problem, IRP)[11]存在一定相似性。然而, 传统的AGV调度研究主要集中在路径规化方面, 通常不考虑末端物料消耗; VRP、IRP问题通常假设末端需求为常数或者服从某一分布, 而混流装配线的末端工位需求通常为一时间序列。
本文以混流汽车生产线为例, 构建了车辆装载与路径规划的联合优化模型以解决混流装配线中点对点配送方式的准时化物料配送问题。给出了该问题的精确算法和启发式算法, 最后进行了仿真分析以验证算法和模型的可行性、有效性。
在混流汽车生产车间, 待装配车辆依次通过各装配工位进行装配。物料超市暂存来自中心仓库的各类物料, 并通过AGV对所负责的生产线子区段进行多批次、小批量的点对点物料配送作业。每个AGV各自负责多个相连工位的准时化物料更新作业, 本文研究单个AGV的准时化物料配送调度问题, 如图1所示。
为了更加清晰地描述混流装配线准时化物料配送问题, 本文作如下假设:①物料配送系统选用节拍时间作为基本时间单位; ②各装配工位仅包含一类零件的装配作业; ③AGV所负责物料配送作业的目标工位集合和各工位的初始库存量已知; ④装配顺序已知, 待装配车辆在各工位的零件需求量依据装配车型而定; ⑤AGV采用无等待搬运策略, 完成前一次配送作业后立刻开始下一次配送; ⑥每次物料配送量不得超过AGV装载能力; ⑦物料超市到各工位间的行车时间已知(包含装、卸载作业耗时); ⑧装配线不允许缺货; ⑨各工位装配耗时均为节拍时间, 装配开始时刻所需零件即刻消耗。
基于上述问题描述, 建立混流装配线准时化物料配送问题的数学模型。为了方便形式化描述, 定义以下数学符号。
问题参数:ψ 为待装配车辆集合(标号p); M为工位集合(标号m); T为生产节拍总数(标号t); ξ p, m为集合ψ 中第p辆待装配车辆在工位m进行装配作业所需消耗的零件数量; τ p, m为第p辆待装配车辆在工位m开始装配的时间; dm为超市与工位m间的行车时间; Am为工位m的初始库存量; Km为AGV装载工位m所需零件的装载能力; Dm, t为t时刻工位m的零件的累积需求量; Γ m, t为t时刻工位m线边零件的累积到达量; Lm, t为t时刻工位m的线边库存水平; ω m为工位m的库存水平权重系数。
决策变量:Υ ={(mi, ni)}表示配送方案, 其中mi和ni分别为第i次配送作业的到达工位和配送量;
此外, 辅助函数μ 1(u, v)、μ 2(u, v)、μ 3(x)定义如下:
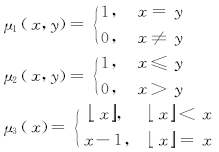
根据上述问题描述、模型假设及符号规定, 对混流装配线准时化物料配送问题建模如下:
目标函数:Minimize Z(Υ )=
约束条件:
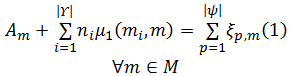
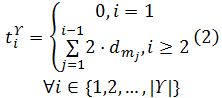
其中:
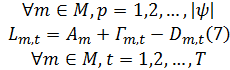
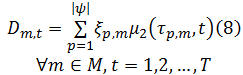
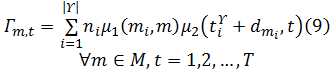
目标函数为最小化物料搬运期间所有工位中的最大加权库存水平, 约束(1)为配送总量约束; 约束(2)为发车时间约束; 约束(3)为装配线不允许缺货约束; 约束(4)为AGV装载能力约束。由式(5)可得生产节拍总数T; 由式(6)可得待装配集合中第p辆待装配车辆在工位m进行装配作业的开始时间τ p, m; 由式(7)可得t时刻工位m的线边库存水平Lm, t, 式(7)中t时刻工位m的物料需求量Dm, t和t时刻工位m的物料累积到达量Γ m, t分别由式(8)和式(9)可得。
为了有效地求解该模型, 给出了该调度问题的两条基本性质。
性质1 给定完整调度方案Υ ={(si, ni)}, ∀ β ≤
通过在部分方案π 后添加其他配送作业以构建完整调度方案从而生成Υ 的邻域Υ ', 若存在
利用性质1, 可在后续的算法设计中进行有效的剪枝操作, 进而减少问题的搜索空间。
性质2 装配线各工位线边库存在进行物料更新时达到局部最大, 在物料更新前一刻达到局部最低, 故给定完整调度方案Υ ={(si, ni)}, 构建局部最低库存量集合Ω , 定义如下:
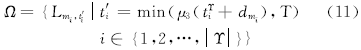
若∃θ < 0(θ ∈ Ω ), 则装配线发生缺货, 该Υ 为不可行解; 否则, Υ 满足装配线不允许缺货约束。
同理, ∀ β ≤
利用性质2, 可判断完整调度方案Υ 及部分方案π 是否满足装配线不允许缺货这一约束; 同时, 若π 导致装配线缺货, 则可进行剪枝操作以减少问题的搜索空间。
为了有效地解决混流装配线准时化物料配送问题, 结合性质1和2, 给出了该问题的回溯法以获得小规模问题的最优解, 具体步骤如下:
Step1 令Υ ← ⌀, χ =(mχ , nχ )← (1, 1), Z* ← +¥ , 转Step2。
Step2 若Υ =⌀且χ =(|M|+1, 1), 转Step8; 否则, 转Step3。
Step3 若χ =(|M|+1, 1), 转Step7; 若nχ +
Step4 记
Step5 若nχ < 1, 令χ ← (1, 1), 转Step2; 若nχ <
Step6 若Υ 不是一个完整的调度方案, 转Step2; 否则, Υ * ← Υ , Z* ← Z(π ), 转Step7。
Step7 若|Υ |> 0, 令去掉Υ 中最后一项搬运作业, 令χ 为当前Υ 中的最后一项搬运作业, ℓ← χ , 转Step5; 否则, 令χ ← (0, 0), ℓ← χ , 转Step5。
Step8 输出Υ * 、Z* , 并结束搜索过程。
以上步骤中, Υ * 、Z* 分别记录当前的最优方案和对应的目标函数值。Step4中设置有两个回溯点, 若当前部分方案通过增加后续一项配送作业所构建的配送方案无法同时满足性质1和2, 则去掉该项搬运作业, 返回前一状态并进行剪枝操作。
为了进一步说明该问题回溯法求解过程, 给出了工位集合M为{1, 2}、装配顺序为车型{1, 2, 3, 1, 2, 3}的算例分析。表1中给出了该算例参数, 包括各车型在每个工位的物料需求量、AGV装载能力Km、物料超市与各工位间的行车耗时dm、各工位的初始水平Am。此外, ω m=1(∀ m∈ M), 图2给出了该算例的搜索过程。
| 表1 算例参数 Table 1 Parameters of proposed example |
由图2可知, 最优方案由{(1, 3), (2, 3), (2, 2), (2, 1)}更新为{(2, 3), (1, 3), (2, 2), (2, 1)}, 最优解由5更新为3; 部分方案{(1, 3), (2, 3), (2, 3)}满足装配线不允许缺货约束, 但由于其Z* 值为5且当前最优解的目标函数值{(1, 3), (2, 3)}为5, 故依据性质1回溯至前一状态 并进行剪枝操作。
通过结合性质1和2设置回溯点并进行剪枝操作, 有效地减少了问题的搜索空间, 并获得了该问题的全局最优解。然而, 随着问题规模的扩大, 搜索空间将会急剧增长, 为此本文构建了改进型离散人工蜂群算法以求解中大规模问题的满意解。
作为近年来兴起的一种新型智能群体算法, 人工蜂群算法(Artificial bee colony, ABC)在连续空间问题优化上得到了有效运用[12]。然而其位置更新策略在离散问题的研究上并不适用, 且在大规模离散问题求解过程中存在局部搜索能力较弱、易早熟收敛等问题。因而, ABC算法在离散化问题的优化上仍具有很大的研究空间。
为了获得混流装配线准时化物配送问题在大规模情形下的满意解, 构建了改进型离散人工蜂群算法(MDABC)算法。应用混沌映射和反向学习技术进行初始化, 以提高初始解的质量; 在邻域搜索阶段引入融合局部搜索和差分进化操作以提升算法的收敛性能, 具体流程如下:
Step1 初始化算法参数, 包括种群规模Ne、迭代次数Sout、停滞代数Pout、调节参数Limit等; 运用混沌映射和反向学习技术初始化蜜源。
Step2 雇佣蜂阶段:采用局部搜索优化当前最优解; 剩余蜜源采用差分进化操作进行优化。
Step3 观察蜂阶段:基于选择蒙特卡罗法, 通过差分进化操作优化当前蜜源。
Step4 侦查蜂阶段:针对当前蜜源中Limit步没有更新的个体进行重新初始化操作。
Step5 若满足算法终止条件, 则终止算法, 并输出最优解; 否则, 转Step2。
蜜源Υ 1, Υ 2, …, Υ Ne采用变长双层整数编码方式, Ne为蜜源(也即雇佣蜂)数量。编码长度
上述编码方式并未考虑装配线不允许缺货这一约束, 考虑到非可行解的存在, 向目标函数Z(Υ )中引入惩罚项, 进而构建函数
式中:σ m(σ m> 0, m∈ M)表示与各工位发生缺货相关的惩罚系数。
蜜源的初始化操作对算法的全局收敛速度和解的质量有着重要影响, 采用随机初始化操作, 一定程度上限制了传统的ABC算法的求解效率。为此, 本文通过融合混沌映射和反向学习技术进行蜜源的初始化操作, 给定种群规模Ne和混沌迭代参数CI, 方案Υ 、
①令Υ ← ⌀, 令i=j=1, r'1=rand(0, 1),
r″1=rand(0, 1)
②repeat
③ for j=1:CI
④ r'j+1=sin(π * r'j), r″j+1=sin(π * r″j)
⑤ end for
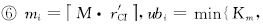
⑦until
⑧
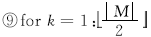
⑩∀ i∈
⑪ end for
基于上述步骤生成{Υ 1, Υ 2, …, Υ Ne}及{
为了克服传统人工蜂群算法搜索深度不足的缺陷, 考虑到当前最优解对算法收敛性能的重要影响, 采用局部搜索操作对当前雇佣蜂群中的最佳个体进行深度搜索, 以强化算法的收敛性能。
给定物料搬运方案Υ , 基于如下约束, 求得方案Υ 的参数(m* , t* , i* )
给定蜜源中的最佳个体Υ best, 令Υ ← Υ best, 求得方案Υ 的参数(m* , t* , i* ); 依据性质1和2, 通过保留前i* -1项配送作业并重构剩余配送作业项生成Υ 的邻域以进行局部搜索, 令Ω =⌀, 给定控制参数∂ , 局部搜索操作如下:
Step1 已知Υ 和i* , Υ '← {(mj, nj)|(mj, nj)∈ Υ , ∀ j< i* }, 构建集合π , 令π ← {Υ '}并转Step2。
Step2 令J(Υ ')={(m, n)|m∈ M, 1≤ n≤ G(Υ ', m)}, 其中G(Υ ', m)=min
Step3 ∀ Λ j∈ π 及ak∈
Step4 令π ←
Step5 若
其中, Ω 用于记录搜索过程中的优秀解(优于当前最优解); 控制参数∂ 用于控制搜索空间, 且与问题规模ψ 正相关, ∂ 越大, 局部搜索所探索的局部解空间越大, 但算法的CPU耗时也越长。
考虑到差分进化算法在求解NP-Hard问题的有效性, 针对当前雇佣蜂种群中的非最优个体, 构建差分进化操作以获得优秀解, 该操作包含变异、交叉、选择三部分, 具体流程如下:
变异操作:已知配送方案Υ , 给定变异概率MR和参数v1< v2< v3(v1> 0, v3< 1), 若rand(0, 1)< MR, 进行如下操作:
Step1 r=rand(0, 1), 若r< v1, 转Step2; 若v1≤ r< v2, 转Step3; 若v2≤ r< v3, 转Step4; 否则, 转Step5。
Step2 任给j1≠ j2(j1、j2∈ {1, 2, …,
Step3 依据
Step4 若∃j1≠ j2( j1、j2∈ {1, 2, …,
Step5 方案Υ 变异结束。
交叉操作:交叉操作采用部分匹配交叉算子, 给定方案Υ 和交叉概率CR, 随机选择当前蜜源中的个体Υ '(Υ '≠ Υ ), 若rand(0, 1)< CR, 进行如下操作:
Step1 随机生成mc∈ M。
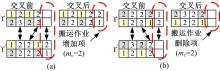
Step2 依次交换Υ 、Υ '中包含工位mc的搬运项, 若Υ 中的含工位mc的搬运项数目少于Υ ', 如图4(a)所示, 将剩余项置于Υ 末尾; 同理, 若Υ 中的含工位mc的搬运项数目多于Υ ', 则取消相应的搬运项, 如图4(b)所示。
Step3 方案Υ 交叉结束。
选择操作:应用贪婪规则, 选取方案Υ 及其经过变异、交叉后的新个体中适应度较优者作为后代个体。
实验部分引用文献[8]中混流装配线准时化物料配送研究的相关参数, 考虑工位数目|M|=5物料配送问题, 表2分别给出了3类车型(A、B、C)在各工位m装配作业的物料消耗量、行车时间dm、初始库存量参数Am、AGV装载能力参数Km, ∀ m∈ M, ω m=1。此外, 车型装配顺序为:A、B、C、A、B、…。
| 表2 仿真实验参数 Table 2 Parameters of simulation experiments |
所有算法均在主频为2.4 GHz、内存4 GB、Intel(R) Core(TM) i5-2430M CPU的便携式计算机上进行仿真实验, 编程环境为Matlab(2013a)。
首先, 进行小规模问题的仿真实验以验证回溯法和MDABC算法的有效性, 问题规模|ψ |(即待装配的车辆的数目)分别设为10、15、20、25。针对各个算例, 回溯法的最大计算时间设为24 h, MDABC算法运行30次, 统计结果如表3所示。
| 表3 小规模算例实验结果 Table 3 Experimental results of small-scale instances |
其3中, 最大偏差表示MDABC算法获得的最劣解与回溯法获得的最优解之差, 最优解百分比为表示MDABC算法获得的最优解次数与实验次数之比。由表3可知, 回溯法能够在给定的计算时间内获得小规模算例的最优解; 同时, MDABC算法的最优解百分比达到90%, 且在问题规模为25时优化结果的最大偏差为1。这两方面分别验证了回溯法和MDABC算法的有效性。
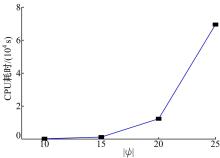
此外, 给出了回溯法求解该问题的CPU耗时, 如图5所示。随着问题规模的扩大, 回溯法的搜索时间急剧增加, 在|ψ |=25的情形下, CPU耗时达到19.3 h。因而, 本文有必要提出改进型智能优化算法以应对中大规模问题的爆炸搜索空间。
令问题规模|ψ |∈ {30, 40, …, 100}, 进行中、大规模问题的仿真实验以验证MDABC算法的有效性。由于本文所研究的调度问题尚无标准算例库, 考虑到该问题与VRP问题具有一定相似性, 故将文献[13, 14]中求解VRP问题相关的遗传算法(Genetic algorithm, GA)和模拟退火算法(Simulated annealing, SA)运用到本文的大规模算例中, 表4对比了MDABC算法的优化结果与GA、SA算法的优化结果。其中, 目标函数值Z取20次试验结果的平均值, PR(Percentage error)表示GA、SA算法优化结果与MDABC算法优化结果的相对误差。
由表4可知, 随着问题规模
| 表4 中大规模算例实验结果 Table 4 Experimental results of small instances of medium and large-scale instances |
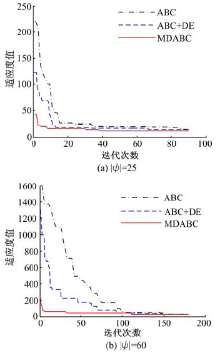
为了验证MDABC算法的收敛性能, 给出了问题规模|ψ |分别为25、60情形下基本人工蜂群算法(ABC)、融合差分进化操作的人工蜂群算法(ABC+DE)以及改进型离散人工蜂群算法(MDABC)的收敛曲线, 如图6所示。
图6中, 3条曲线的初始位置表征了3种算法初始解的质量, 由于MDABC算法融合了混沌映射和反向学习初始化方法, 其初始解的质量要显著优于采用随机初始化方法的其他两种算法。此外, 在小规模情形下, 3种算法都能快速搜索到问题的最优解, 如图6(a)所示; 然而, 随着问题规模的扩大, 本文所提出的差分进化和局部搜索操作的嵌入一定程度上提高了算法的搜索深度, 提高了ABC算法的收敛速度, 使得MDABC能够快速搜索到问题的满意解, 如图6(b)所示。实验结果有效地验证了MDABC算法的收敛性能。
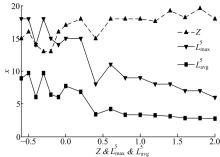
令问题规模|ψ |=30, ∀ m≤ 4, 保持ω m不变, 给定
由图7可知, 当ω 5较小时, 工位5库存的库存水平(最高库存水平和平均库存水平)随ω 5变化趋势不明显; 随着ω 5增大至一定值时, 工位5库存的库存水平与ω 5呈负相关。此外, 随着ω 5值的增加, 当x≥ 1时有等式Z=ω 5·
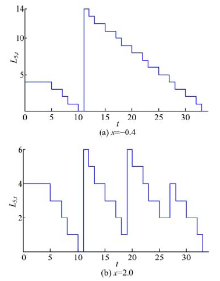
如图8所示, 给出工位5线边库存状况L5, t变化的阶梯图, 图8(a)(b)分别表示x取值为-0.4、2.0情形下的算例。由图8(a)可知, x=-0.4时, 采用接近AGV装载能力K5的搬运量进行工位5的物料更新作业, 以尽可能提高其他工位准时化程度; 由图8(b)可知, x=2.0时, 工位5的物料更新作业成为整个物料搬运系统的瓶颈, 故每次物料配送量远小于AGV装载能力K5, 准时化程度高, 这在一定程度验证了本文准时化配送模型的有效性。
本文以混流装配线的物料配送问题为背景, 基于搬运设备的装载能力及装配线的不允许缺货约束, 充分考虑车辆装载问题和路径规划问题, 从而构建了准时化物料配送模型。在算法部分, 构建了回溯搜索算法以获得小规模问题的满意解; 同时为了应对中大规模问题搜索空间的组合爆炸特性, 提出了MDABC算法, 在邻域搜索部分融入了局部搜索和差分进化操作以改善基本ABC算法的收敛性能。仿真实验结果表明:回溯法和MDABC算法能够有效地解决装配线准时化物料配送问题, 并将混流生产线的线边库存量控制在较低水平。后续研究考虑多台搬运车的联合调度问题以及包含停机等不确定因素的动态调度问题。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|