基于时间衰减的协同过滤推荐算法

引用本文

董立岩, 王越群, 贺嘉楠, 孙铭会, 李永丽. 基于时间衰减的协同过滤推荐算法. 2017, 47(4): 1268-1272
DONG Li-yan, WANG Yue-qun, HE Jia-nan, SUN Ming-hui, LI Yong-li. Collaborative filtering recommendation algorithm based on time decay. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1268-1272 复制到剪切板

Permissions

基于时间衰减的协同过滤推荐算法

董立岩^1,², 王越群¹, 贺嘉楠¹, 孙铭会^1,², 李永丽³

1.吉林大学计算机科学与技术学院,长春 130012

2.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

3.东北师范大学信息科学与技术学院,长春 130117

通讯作者：孙铭会(1983-),男,讲师,博士.研究方向:人机交互,数据挖掘.E-mail:smh@jlu.edu.cn

作者简介:董立岩(1966-),男,教授,博士生导师.研究方向:数据挖掘.E-mail:dongly@jlu.edu.cn

基金:国家自然科学基金项目(61272209,61300145).

摘要

针对传统的协同过滤算法在计算相似度时未考虑时间因素的影响,导致推荐结果不准确的问题,本文提出将时间因素融入用户项目评分矩阵中,以解决兴趣衰减的问题。首先将遗忘曲线和记忆周期作为时间因素融入算法之中,将艾宾浩斯遗忘曲线用于指数函数拟合,从而获得时间与兴趣衰减的函数关系,以此用于优化用户项目的评分。并将改进的评分矩阵应用到基于项目的协同过滤推荐算法中进行推荐。在评分中加入记忆周期的影响,让目标用户对待预测的项目评分预测更为准确。实验结果表明,改进后的基于时间衰减协同过滤算法在准确性方面有显著的提高。

关键词: 计算机系统结构; 协同过滤; 推荐算法; 时间衰减曲线; 相似度

中图分类号:TP393 文献标志码:A 文章编号:1671-5497(2017)04-1268-05

Collaborative filtering recommendation algorithm based on time decay

DONG Li-yan^1,², WANG Yue-qun¹, HE Jia-nan¹, SUN Ming-hui^1,², LI Yong-li³

1.College of Computer Science and Technology,Jilin University,Changchun 130012,China

2.Key Laboratory of Symbol Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun 130012

3.School of Computer Science and Information Technology,Northeast Normal University,Changchun 130117,China

Abstract

Since time factor is not considered in calculating score matrix in traditional collaborative filtering, the accuracy for recommendation is limited. In order to solve this problem, we propose a method, which integrates the time factor into the user score matrix. In this method, first the forgetting curve and the memory period are incorporated into the algorithm as the time factor. Then Ebbinghaus forgetting curve is fitted with potential function. This way can get more correct correlation function between time and interest decay. Finally all the results are imported into the user score matrix, and then the matrix is applied in collaborative filtering recommendation algorithm. The factors, which add the memory cycle to the score, make the target user predict the predicted project score more accurately. The experiments show that the results obtained with the proposed method are much more accurate than that of the original one.

Keyword: computer systems organization; collaborative filtering(CF); recommendation algorithm; time decay curve; accuracy

Show Figures

0 引言

推荐系统在电子商务领域占据着十分重要的角色, 它能够很好地处理信息过载的问题。目前, 推荐系统已经被不同程度的应用在各个大型的电商系统中^[1]。推荐系统的应用价值很高, 好的推荐系统能够为商家带来高额的商业利润, 而推荐系统的核心便是推荐算法。推荐算法涉及到数学、人工智能、市场营销、认知、管理等多个学科的知识, 推荐算法已经成为计算机领域具有挑战性的研究课题之一^[2]。

协同过滤的推荐算法主要是通过相似度计算, 寻找与目标用户相似度最高的用户, 将用户感兴趣的内容或相似度较高的其他内容推荐给最终用户^[3]。基于协同过滤的推荐方法忽略了用户和项目自身的很多特征, 基于内容的推荐算法通过对用户和项目自身特征的充分分析和合理利用来获得更加理想的推荐效果。基于图结构的推荐算法是将用户-项目矩阵抽象为一个二部图, 将用户和项目分别用节点表示, 用户对项目的评分用图中的边表示, 结合资源分配的思想, 通过对该图的计算来为目标用户做推荐。混合推荐算法则是对以上几种推荐算法的组合。

汪静等^[4]提出了融入共同评分及相似性权重的推荐算法。Choi等^[5]提出在对项目的评分时, 将共同评分及待预测物品的相似性作为权重融入协同过滤推荐算法。朱思丞等^[6]提出将时间因素作为影响因子融入算法中, 使用户的兴趣具有时效性。

本文在传统协同过滤算法基础上, 引入时间影响因素, 将艾宾浩斯遗忘曲线作为时间函数融入改进的算法之中, 并增加记忆周期影响因子, 使得项目的评分预测更为精确。

1 基于时间衰减的协同过滤算法

由于传统的算法没有考虑用户的兴趣与时间的关系, 这样会导致推荐系统的推荐结果有很大的偏差^[7]。因为人们的兴趣会随着年龄的增长, 环境的转变而有所变化, 兴趣并不是一成不变, 影响兴趣的因素过多, 时间是最重要的影响因素之一。在文献[8, 9]中, 把时间作为因变量融合到算法中。

本文把反映人们遗忘规律的艾宾浩斯遗忘曲线融入到算法当中, 进而改善协同规律算法。遗忘曲线表示人们的爱好或者记忆随着时间节点会慢慢减弱^[10]。本文对算法的改进加入了记忆周期^[11], 在遗忘过程中, 如果重复某个记忆, 则会加深这个记忆并达到很久都不能遗忘的状态。

1.1 艾宾浩斯遗忘曲线拟合

本文通过Python的matplotlib包, 对艾宾浩斯遗忘曲线进行拟合, 输入曲线数据, 即天数和记忆量, 观察形状, 可以用指数函数进行拟合, 结果如图1所示。

	Figure Option View Download New Window
	图1 Python曲线拟合图Fig.1 Python curve fitting

最终的艾宾浩斯遗忘曲线的拟合公式为:

$\begin{matrix} Wt = 68.2 e^{- 0.0445 x} + 33.2 e^{- 0.12 \times 10^{- 4} x} (1) \end{matrix}$

式(1)为时间x与兴趣程度Wt的一个映射关系。

$\begin{matrix} X = \frac{T_{\max} - T_{ui}}{60} (2) \end{matrix}$

式中: T_ui表示了用户u对项目i评分的时间, 因为在拟合的艾宾浩斯指数曲线中, 单位min。

结合式(1)(2), 获得用户兴趣随时间变化的函数:

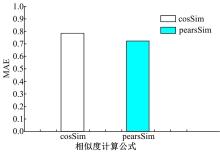
$\begin{matrix} Wt = 68.2 e^{- 0.0445 \times \frac{T_{\max} - T_{ui}}{60}} + 33.2 e^{- 0.12 \times 10^{- 4} \times \frac{T_{\max} - T_{ui}}{60}} (3) \end{matrix}$

1.2 相似度计算

本文采用余弦相似性及皮尔森相关系数来判断两个项目之间的相似度, 采用传统算法计算相似度的平均绝对偏差如图2所示。

	Figure Option View Download New Window
	图2 传统算法下不同相似度算法的比较Fig.2 Comparing the different similarity algorithm under the traditional method

通过以上实验对比结果可知, 采用皮尔森相关系数方法计算平均绝对偏差更理想, 相似度的计算结果更好。

皮尔森相关系数的改进公式为:

$\begin{matrix} \begin{matrix} sim (x, y) = \\ \frac{\sum_{S \in Sx, y} (R_{x, s} * Wt - \bar{R_{x}}) \times (R_{y, s} \times Wt - \bar{R_{y}})}{\sqrt[]{\sum_{S \in Sx, y} (R_{x, s} {\times Wt - \bar{R_{x}})}^{2}} \sqrt[]{\sum_{S \in Sx, y} (R_{y, s} {\times Wt - \bar{R_{y}})}^{2}}} (4) \end{matrix} \end{matrix}$

1.3 记忆周期因子

记忆周期表示用户对当前项目的熟悉程度。若记忆已经转换为长久记忆, 即使长时间没有接触, 记忆也不会有所衰减^{[12, 13]}。通过加入记忆周期因子, 可对时间衰减进行修正。

设用户集U={U₁, U₂, …, U_n}, 项目集合M={M₁, M₂, …, M_n}。

记忆周期因子的表达式如式(7)所示:

$\begin{matrix} α = \overset{Grade}{\sum_{M_{k} \in M (J, i . type)}} \times \frac{M (J, i . type)}{M (J)} \times 10^{- 2} (5) \end{matrix}$

式中:Grade(M_i)表示目标用户对项目M_i 的评分, M(J, i.type)表示用户J参的项目, 其类型与项目i的类型相同。M(J, i.type)M(J)。本文将 $\begin{matrix} α \end{matrix}$ 的值定义在10^-2的级别上。

最终的评分预测公式为:

$\begin{matrix} g_{r, s} = \frac{\sum_{u_{i} \in U} Sim (u, u_{i}) g_{ui, s}}{N} + α (6) \end{matrix}$

式中:Sim(u, u_i)表示目标用户u和用户u_i 的相似度; N为用户u及用户u_i 共同参与的项目数; g_{ui, s} 为用户u_i 赋予项目s的分值。

1.4 算法描述

基于时间衰减的协同过滤算法如下:

基于时间衰减的CF算法

输入:数据集S

输出:推荐影片的评分矩阵并选出Top20

1 for M=Movie(U_i)∩ Movie(U_j)

//遍历数据集S中的用户

2 φ _t= $\begin{matrix} \frac{T_{\max} - T_{ui}}{60} \end{matrix}$

//计算用户每个项目的评分时间项

3 根据式(3), 计算Wt, 即每个用户对于已经评分的项目的遗忘值

4 end for //遍历结束

5 for U_i, U_j∈ S

//遍历数据集中的用户

6 M=Movie(U_i)∩ Movie(U_j)

//找到用户i和用户j共同评分过的项目

7 for M_a∈ M

//遍历项目集中共同评分过的项目

8 通过式(4)计算用户间相似度

9 end for

10 end for

11 选出每个用户相似度最高的10个用户, 获得相似用户矩阵USER

12 for U_i∈ USER

//遍历相似用户

13 Mnew=Movie(U_i)∩ !Movie(U_j)

//找到相似用户接触过但是目标用户没接触的项目, 获取项目集合Mnew

14 通过式(6)预测目标用户对Mnew的评分, 获取评分最高的N个MnewTopN

15 end for

16 return MnewTopN

2 实验分析

2.1 实验数据

实验所用数据集为MovieLens ml-1M版本数据集, 由984个用户, 2000个电影, 以及10万条评分组成。

根据数据集计算出每个用户评论每个项目的时间段, 形成用户行为的时间表, 如表1所示。

表1 用户对项目的评分时间Time表 Table 1 User ratings for item time table

2.2 实验评测标准

本文实验采用平均绝对偏差(MAE)和命中率^[9]两种方案来进行改进后算法优劣的结果评定。

平均绝对误差计算公式为:

$\begin{matrix} MAE = \frac{\sum u, iT | r_{u, i} - P_{u, i} |}{| T |} (7) \end{matrix}$

式中:r_{u, i}为用户u的实际评分值; P_{u, i}为用户u的预测评分值。

命中率的计算即判断为用户推荐的 $\begin{matrix} TopN \end{matrix}$ 个项目中, 目标用户已经为其打分的项目所占的比例, 比例越高, 说明推荐的结果越优^{[14, 15]}。

$\begin{matrix} precision = \frac{testing ⋂ TopN}{N} = \frac{Mits}{N} (8) \end{matrix}$

由式(7)和(8)可以判定出, MAE与推荐效果成负相关, 即MAE值越小, 推荐效果越良好。命中率与推荐效果成正相关, 命中率越高, 推荐效果越良好。

2.3 实验结果与分析

本文改进的算法与传统的算法相比, 实验结果如图3所示。

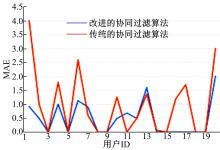
	Figure Option View Download New Window
	图3 时间衰减项对协同过滤的影响Fig.3 The influence of time decay terms on CF

图3是对所有用户的MAE取出并进行均值计算获得的最终结果, 现随机取出20个用户, 用折线图来表示其MAE的一个趋势, 如图4所示更直观地看出新算法的MAE值

	Figure Option View Download New Window
	图4 抽样用户的MAEFig.4 Sampling the user's MAE

在总体上普遍小于传统CF算法。

由图3和图4可以看出, 把艾宾浩斯曲线引入作为时间曲线后以及加入记忆周期影响因子后, 其结果无论是对平均值还是对随机抽样的个体都有很好的改进, MAE值小了很多, 说明推荐结果优秀了很多。因此, 可以看出在协同过滤推荐中, 加入时间因素会使推荐结果更理想。

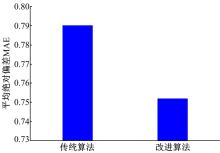
本文的改进算法与传统的算法相比, 在推荐准确度方面有所提高, 实验结果如图5所示。

由图5可以看出, 基于改进的协同过滤算法比传统的协同过滤算法在条件相同的情况下, 命中率更高。

	Figure Option View Download New Window
	图5 时间衰减项对协同过滤推荐结果命中率的影响Fig.5 The influence of time decay on the hit rate of CF

3 结束语

本文将兴趣的时效性以艾宾浩斯曲线的形式融合到算法之中, 将时间衰减因素融合到皮尔森系数中。在后期评分预测时, 融入了记忆周期的影响因子。实验结果表明, 融合时间衰减因素的协同过滤算法在其他条件一致的情况下, 其推荐结果要优于未考虑时间因素的协同过滤算法, 在一定程度上可以为目标用户更好的推荐结果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lyu L, Medo M, Yeung C H, et al. Recommender systems[J]. Physics Reports, 2012, 519(1): 1-49. [本文引用:1]
[2]	景民昌. 从ACM RecSys'2014国际会议看推荐系统的热点和发展[J]. 现代情报, 2015, 35(4): 41-45. Jing Min-chang. Hot topics and trends of recommender system research: areview on ACM RecSys'2014 annual meeting[J]. Journal of Modern Information, 2015, 35(4): 41-45. [本文引用:1]
[3]	冷亚军, 陆青, 梁昌勇. 基于结构相似性的协同过滤推荐算法[J]. 小型微型计算机系统, 2015, 36(10): 2266-2269. Leng Ya-jun, Lu Qing, Liang Chang-yong. Collaborative filtering recommendation algorithm based on structure similarity[J]. Journal of Chinese Computer Systems, 2015, 36(10): 2266-2269. [本文引用:1]
[4]	汪静, 印鉴, 郑利荣, 等. 基于共同评分和相似性权重的协同过滤推荐算法[J]. 计算机科学, 2010, 37(2): 99-104. Wang Jing, Yin Jian, Zheng Li-rong, et al. Collaborative filtering recommendation algorithm based on co-ratings and similarity weight[J]. Computer Science, 2010, 37(2): 99-104. [本文引用:1]
[5]	Choi K, Suh Y. A new similarity function for selecting neighbors for each target item in collaborative filtering[J]. Knowledge-Based Systems, 2013, 37(1): 146-153. [本文引用:1]
[6]	朱思丞, 黄瑛, 孙志锋. 推荐算法时间动态特性研究进展[J]. 工业控制计算, 2015, 28(8): 99-100. Zhu Si-cheng, Huang Ying, Sun Zhi-feng. Research on progress of time-based dynamic recommender system[J]. Industrial Control Computer, 2015, 28(8): 99-100. [本文引用:1]
[7]	Seminario C E, Wilson D C. Attacking item-based recommender systems with power items[C]//Proceedings of the 8th ACM Conference on Recommender Systems, New York, 2014: 57-64. [本文引用:1]
[8]	Zhang Xiang-liang, Lee T, Pitsilis G. Securing recommender systems against shilling attacks using social-based clustering[J]. Journal of Computer Science and Technology, 2013, 28(4): 616-624. [本文引用:1]
[9]	Zhang L, Xu J, Li C. A rand om-walk based recommendation algorithm considering item categories[J]. Neurocomputing, 2013, 120(10): 391-396. [本文引用:1]
[10]	Bobadilla J, Ortega F, Hernand o A, et al. Recommender systems survey[J]. Knowledge-Based Systems , 2013, 46: 109-132. [本文引用:1]
[11]	Qian X, Feng H, Zhao G, et al. Personalized recommendation combining user interest and social circle[J]. IEEE transactions on Knowledge and Data Engineering, 2014, 26(7): 1763-1777. [本文引用:1]
[12]	Zeng L, Lin L. An Interactive vocabulary learning system based on word frequency lists and ebbinghaus' curve of forgetting[C]//Digital Media and Digital Content Management(DMDCM), NJ: IEEE Computer Society Press, 2011: 313-317. [本文引用:1]
[13]	Wang J, Hu X, Li Z, et al. Learning to recommend questions based on public interest[C]//ACM International Conference on Information and Knowledge Management, NY: ACM Press, 2011: 2029-2032. [本文引用:1]
[14]	Guo Y, Huang M, Sun L. A collaborative filtering algorithm of selecting neighbors for each target item[C]//Web Information System and Application Conference, NJ: IEEE Computer Society Press, 2014: 139-143. [本文引用:1]
[15]	Li Z, Lin J. An analysis of the subscription in user-generated content video systems[C]//International Conference on Computer Communications and Networks, Washington: IEEE Computer Society Press, 2012: 1-7. [本文引用:1]

2012

0.0

... 目前,推荐系统已经被不同程度的应用在各个大型的电商系统中^[1] ...

2015

0.0

. 2015, 35(4):41-45 DOI:doi:10.3969/j.issn.1008-0821.2015.04.009

Hot topics and trends of recommender system research:areview on ACM RecSys'2014 annual meeting

从ACM RecSys'2014国际会议看推荐系统的热点和发展

Jing Min-chang.

景民昌

摘　要：美国计算机学会每年举办的RecSys年会是最重要的推荐系统国际会议之一,其内容体现了当前推荐系统研究的热点和发展趋势。本文分析RecSys’2014年会的论文内容和主题,从推荐系统的新应用、情景敏感推荐、冷启动和混合推荐、安全和用户隐私、推荐系统评估、多样性和新颖性、推荐理论和方法、排序和Top-N推荐、矩阵分解等9个方面对会议进行综述,总结当前推荐系统研究的特点,认为混合推荐是未来推荐系统研究的主要方向。

... 推荐算法涉及到数学、人工智能、市场营销、认知、管理等多个学科的知识,推荐算法已经成为计算机领域具有挑战性的研究课题之一^[2] ...

2015

0.0

. 2015, 36(10):2266-2269

Collaborative filtering recommendation algorithm based on structure similarity

基于结构相似性的协同过滤推荐算法

Leng Ya-jun , Lu Qing , Liang Chang-yong.

冷亚军, 陆青, 梁昌勇

Due to highdimensional and sparse preference vectors,the accuracy of traditional similarity methods is low.In this paper,we propose a novel similarity method:twophase similarity computation algorithm.Definitions of rating difference and difference certainty are given,and preference similarity is obtained.Based on the preference similarity,the structure similarity is computed.Structure similarity is used to modify the initial relationships between users,which makes the similarity computation more accurate.The proposed method is applied to collaborative filtering recommendation,experiments are carried out on the MovieLens dataset.The results show that,compared to the traditional similarity methods,the proposed method is more accurate and can improve recommendation quality of collaborative filtering significantly.

评分向量的高维、稀疏,使得传统相似性度量方法的准确性较差.提出一种新的相似性计算方法—两阶段相似性计算算法.首先定义评分差异和差异确定度,得到用户偏好相似性;然后根据偏好相似性计算用户间的结构相似性,使用结构相似性对用户初始相似关系进行修正,使相似性计算结果更加合理.将本文方法应用于协同过滤推荐,在MovieLens数据集上进行了实验.实验结果表明,与传统的相似性度量方法相比,新方法具有更高的准确性,可以显著提高协同过滤算法的推荐质量.

... 协同过滤的推荐算法主要是通过相似度计算,寻找与目标用户相似度最高的用户,将用户感兴趣的内容或相似度较高的其他内容推荐给最终用户^[3] ...

2010

0.0

. 2010, 37(2):99-104

Collaborative filtering recommendation algorithm based on co-ratings and similarity weight

基于共同评分和相似性权重的协同过滤推荐算法

Wang Jing , Yin Jian , Zheng Li-rong

汪静, 印鉴, 郑利荣

... 汪静等^[4]提出了融入共同评分及相似性权重的推荐算法 ...

2013

0.0

... Choi等^[5]提出在对项目的评分时,将共同评分及待预测物品的相似性作为权重融入协同过滤推荐算法 ...

2015

0.0

. 2015, 28(8):99-100

Research on progress of time-based dynamic recommender system

推荐算法时间动态特性研究进展

Zhu Si-cheng , Huang Ying , Sun Zhi-feng.

朱思丞, 黄瑛, 孙志锋

传统推荐算法没有考虑时间效应的影响,而随着用户兴趣、产品流行度等变化,会使得推荐效果受到影响。近年来,越来越多的研究者开始关注推荐系统动态特性,时间信息对推荐系统有重要的作用,将回顾推荐系统主要算法,研究静态模型存在的问题,详细介绍近年来国内外动态推荐算法的研究进展,为后续研究提供参考。

... 朱思丞等^[6]提出将时间因素作为影响因子融入算法中,使用户的兴趣具有时效性 ...

2014

0.0

... 1 基于时间衰减的协同过滤算法由于传统的算法没有考虑用户的兴趣与时间的关系,这样会导致推荐系统的推荐结果有很大的偏差^[7] ...

2013

0.0

2013

0.0

... 2 实验评测标准本文实验采用平均绝对偏差(MAE)和命中率^[9]两种方案来进行改进后算法优劣的结果评定 ...

2013

0.0

... 遗忘曲线表示人们的爱好或者记忆随着时间节点会慢慢减弱^[10] ...

2014

0.0

... 本文对算法的改进加入了记忆周期^[11],在遗忘过程中,如果重复某个记忆,则会加深这个记忆并达到很久都不能遗忘的状态 ...

2011

0.0

... 若记忆已经转换为长久记忆,即使长时间没有接触,记忆也不会有所衰减^[12,13] ...

2011

0.0

... 若记忆已经转换为长久记忆,即使长时间没有接触,记忆也不会有所衰减^[12,13] ...

2014

0.0

... 命中率的计算即判断为用户推荐的 TopN个项目中,目标用户已经为其打分的项目所占的比例,比例越高,说明推荐的结果越优^[14,15] ...

2012

0.0

... 命中率的计算即判断为用户推荐的 TopN个项目中,目标用户已经为其打分的项目所占的比例,比例越高,说明推荐的结果越优^[14,15] ...