几何约束求解的扩展C-树分解法

引用本文

李文辉, 孙明玉, 曹春红. 几何约束求解的扩展C-树分解法. 2017, 47(4): 1273-1279
LI Wen-hui, SUN Ming-yu, CAO Chun-hong. Extension C-tree decomposition method for geometric constraint solving. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1273-1279 复制到剪切板

Permissions

几何约束求解的扩展C-树分解法

李文辉¹, 孙明玉¹, 曹春红²

1.吉林大学计算机科学与技术学院,长春30012

2.东北大学计算机科学与工程学院,沈阳110819

通讯作者：孙明玉(1978-),男,讲师,博士.研究方向:计算机辅助设计,计算机图形学.E-mail:sunmingyu370@sohu.com

作者简介:李文辉(1961-)男,教授,博士生导师.研究方向:计算机辅助设计,计算机图形学.E-mail:liwh@jlu.edu.cn

基金:国家自然科学基金项目(61300096); 吉林省科技厅发展计划项目(20140101181JC).

摘要

为了有效分解几何约束系统,本文提出了一种基于增量LMA(ILMA)算法的扩展C-树分解法,该方法将几何约束系统分解为一棵扩展C-树。与C-树分解法相比,该方法能够保证以任意装配几何约束的方式构造的扩展C-树是几何约束系统的最大化分解。实例分解结果表明:将本文方法应用于几何约束求解是行之有效的。

关键词: 计算机应用; 几何约束求解; 扩展C-树; 增量LMA算法; 广义构造序列

中图分类号:TP391.7 文献标志码:A 文章编号:1671-5497(2017)04-1273-07

Extension C-tree decomposition method for geometric constraint solving

LI Wen-hui¹, SUN Ming-yu¹, CAO Chun-hong²

1.College of Computer Science and Technology, Jilin University,Changchun 130012, China

2.College of Computer Science and Engineering, Northeastern University, Shenyang 110819, China

Abstract

A decomposition method of the extended C-Tree based on the increment LMA (ILMA) algorithm was proposed. The method decomposes a geometric constraint system into an extended C-Tree. In comparison with the C-Tree decomposition method, the proposed method can ensure that an extended C-Tree is inevitably the maximum decomposition of the geometric constraint system when constructing it in any way of assembling geometric constraints. Research results show that the proposed method is effective when it is applied to GCS.

Keyword: computer application; geometric constraint solving(GCS); extended C-Tree; incremental LMA algorithm; generalize construction sequence

Show Figures

0 引言

几何约束求解(Geometric constraint solving, GCS)可理解为几何造型(如:企业产品模型、分子结构造型、工程设计用图等)设计的自动化。它作为现代参数化、变量化设计的核心体系和人工智能领域的重要研究分支被广泛应用于各类产品造型、装配设计、虚拟现实、运动学分析、化学分子建模、机器人动力学和教学几何等诸多应用领域, 是现代计算机辅助设计(Computer aided design, CAD)和计算机辅助制造(Computer aided manufacture, CAM)的重要标志之一。

经过国内外研究人员30余年的不懈努力, 几何约束求解已经取得了较多具有针对性的突破, 能够有效解决设计时所面临的相当一部分问题。但距离适合所有几何约束系统求解的一般化方法仍然存在差距, 实现完整、有效和稳定的几何约束求解技术仍须做进一步深入研究。目前, 几何约束求解方法主要包括:数值方法^{[1, 2, 3]}、符号代数法^[4]、基于规则的方法^[5]和基于图论的方法^[6]4类。求解通常采用“ 分而治之” 的策略将一个复杂几何约束系统分解为一系列独立可解的子域, 再采用代数的或几何的方法分别求解这些子域, 最后将各个独立的解合并来获得原有几何约束系统的解。实际应用中, 往往是几种方法混合使用才能达到更好的效果。基于图论的几何约束方法求解效率高、稳定性好, 在各类方法中占据主导地位。

Owen针对具有循环约束的几何约束系统提出第一个经典分解算法— — 三角分解法^{[7, 8]}。该方法基于关节点、双连通和三连通概念, 将几何约束系统分解为三角形结构的子域集合, 并结合深度和广度优先搜索策略, 自顶向下地分割几何约束图。Fudos和Hoffmann等^{[9, 10, 11]}提出了基于簇合并的分解方法。这里, 簇指包含三角形结构的良约束子域, 对簇进行合并, 能够获得规模更大的簇。

Owen和Hoffmann方法的本质是用三角形结构的子域作为求解的基本构型。为克服这种只能求解包含三角形结构子域的限制, Hoffmann等^[12]又使用改进的最大流算法来发现几何约束系统中最小的可解刚体。在此基础之上, 提出改进的边界前沿算法(MFA)^{[13, 14]}, 是几何约束系统分解的一个更一般的方法。Samy等^[15]也在最大流算法基础上提出了一种较MFA算法简化的核构架规约分解法。

文献^[16]基于连通度分析, 提出了一种LMA算法, 该方法由最大B-匹配将几何约束系统分解为一般的广义构造序列, 是第一个处理几何约束系统的一般化方法。它能够分解任意结构的良约束几何约束系统, 准确判断几何约束系统的约束属性(良约束、欠约束和过约束), 相比于一些几何约束求解方法, 它适用范围广、概念简单。广义构造序列在形式上依赖于初始子序列的选择且不能将算法局部地应用于每一个由显示的良约束割图所分离的子域, 往往使系统不能被最大化分解。

为此, 文献^[17]基于局部的LMA算法和启发式算法提出一种C-树分解法, 该方法将良约束几何约束系统分解为一棵C-树, 较好地使用了隐式的几何约束, 并应用启发式算法搜索已定义结构(如三角形结构)的子域作为每次分解剩余子域时LMA算法的初始子序列。C-树是否是最大化分解, 取决于将LMA算法应用于剩余子域时, 其是否包含了已定义结构的子域。

本文提出了一种基于增量LMA(ILMA)算法的几何约束系统分解法构造扩展C-树, 使获得的扩展C-树总是系统的最大化分解, 研究结果表明:将该方法应用几何约束求解是行之有效的。

1 系统分解结构

1.1 基本概念

定义1 使用几何约束图G=(V(G), E(G))表示一个几何约束系统。其中, V(G)是顶点集, 与约束系统的几何基元相对应; E(G)是边集, 与两两几何基元间的几何约束相对应。

定义2 给定几何约束图G, 几何基元顶点v∈ V(G)的自由度指确定该顶点所需要的独立参数的个数。使用DOF(v)表示该顶点v的自由度。

定义3 给定几何约束图G, 几何约束边e⊆E(G)的约束度指被该边所消除的顶点自由度数量。使用DOC(e)表示该边e的约束度。

根据定义2和定义3, 可得几何约束图G的自由度

$\begin{matrix} DOF (G) = \sum_{v \in V (G)} DOF (v) - \sum_{e \in E (G)} DOC (e) \end{matrix}$

定义4 称一个几何约束图G为结构:①良约束, 若DOF(G)=R, 并且对图G的任意导出子图G'满足DOF(G')≥ R; ②过约束, 若存在图G的至少一个导出子图G'满足DOF(G')< R; ③欠约束, 若图G不是过约束的, 并且满足DOF(G)> R。其中, R在二维和三维空间的取值分别为3和6。

若G的几何约束系统分别包含了有限解、无穷解和无解, 则G分别是几何上良约束、欠约束和过约束的。绝大多数研究认为:结构可解性与几何可解性等价。因此, 本文中的良约束、欠约束和过约束也建立在结构可解性上。

若G中的两个几何基元顶点v_i和v_j以及关联v_i和v_j的几何约束边e_ij满足DOF(v_i)=DOF(v_j)=DOC(e_ij), 则v_i和v_j作为一个几何基元v_i参与求解。此时, 称合并后的v_i为一个宏几何基元^[18]。如二维空间的点点重合约束、两平行直线的距离约束; 三维空间的点点重合约束、两平行平面间的距离约束等等。算法1描述了对图G进行合并的过程。

算法1 合并几何约束图G

步骤1 访问G的未被访问几何基元顶点v_i, 遍历与v_i连接的顶点集V_vi, 对于v_j∈ V_vi, 如果v_j满足DOF(v_i)=DOF(v_j)且关联v_i和v_j的边e_ij满足DOF(v_i)=DOC(e_ij), 则首先, 拆卸e_ij; 其次, 使其他关联v_j的边关联v_i; 最后, 拆卸v_j;

步骤2 如果G中仍包含未访问的几何基元顶点, 则转步骤1; 否则, 算法终止。

记合并后的几何约束图仍为G, 分解针对该图G进行, 其顶点集的每一元素均视为几何基元顶点。

1.2 广义构造序列

LMA算法提出了饱和顶点的概念, 指出:若连通图的一个几何约束顶点的约束度或一个几何基元顶点的自由度等于与它相关联的边的权值之和, 则称该顶点为饱和顶点; 否则为非饱和顶点。当且仅当该连通图包含了非饱和几何基元顶点时, 该约束系统是欠约束的; 当且仅当该连通图包含了非饱和几何约束顶点时, 该约束系统是过约束的。LMA方法确定了几何约束系统中几何基元的广义构造序列。

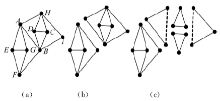
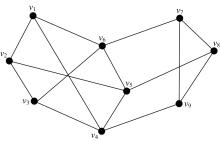
图1为使用LMA算法分解由点和距离约束构成的二维几何约束图实例, 其中(b)和(c)分别为选取AB和CD作为初始子序列时系统的分解结果。(c)是基于该方法的最优分解, 但绝非最大化分解。

	Figure Option View Download New Window
	图1 LMA算法的分解实例Fig.1 An decomposition example of LMA algorithm

定义 5几何约束系统的良约束图G_w=(V(G_w, E(G_w))的广义构造序列指具有如下表达形式的求解序:

$\begin{matrix} GC = G C_{1}, G C_{2}, \dots, G C_{n} \end{matrix}$

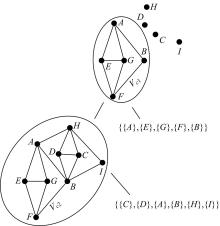
其中, GC_i为一组几何基元顶点集, 该顶点集满足:①若1≤ i≤ n, 则B_i= $\begin{matrix} \cup_{k}^{=} \end{matrix}$ GC_k为良约束子域; ②不存在满足条件①的真子集。

定义中, V(G_w)为几何基元顶点集, E(G_w))为几何约束边集。图1所示实例中, (b)和(c)的广义构造序列分别为{{A, B, E, F, G}, {C, D, H, I}}和{{C}, {D}, {B}, {H}, {A}, {I}, {E, F, G}}。求解过程中, 可依元素顺序依次装配满足约束的几何基元或几何基元组。能够看出, 应用C-树分解法时, 最大化分解的子广义构造序列集为{{{C}, {D}, {B}, {H}, {A}, {I}}, {{E}, {F}, {G}, {A}, {B}}}, 需要求解的子约束方程组中方程的最大数量仅为1, 它使求解的计算量大幅度降低。

1.3 扩展C-树

本文对文献^[17]中C-树的定义予以扩展, 在引入增量LMA(ILMA)算法基础上, 由搜索装配边的最大簇和以复合顶点的边缘顶点为界获取增广良约束子域的广义构造序列来构造扩展C-树, 该扩展C-树必是几何约束系统的最大化分解。

定义6 假设G_sw, G_bc均是几何约束图G的良约束子域, 且G_sw⊆G_bc。称G_bc为G的包含G_sw的簇。若V_-=V(G_bc)-V(G_sw)不为空, V(G_sw)先于V_-构造, 则V_-可序列化构造。

定义7 封装几何约束图G中某子域G_s的顶点对象称为复合顶点V_c。

定义8 若存在几何约束图G, G_s, G_r和G_cu满足:G_s⊂G, G_r⊆G, G=G_s∪ G_r和G_cu=G_s∩ G_r, 则称G_s为G的一个分离图, G_cu为分离G_s的割图。使用S(G_s, G)表示从G分离G_s的剩余子图。

假设G(N)为二叉树中节点N的不必是连通的几何约束图, 同时指出:仅由单一几何基元顶点构成的几何约束图是几何约束图的特例。

定义9 良约束几何约束图G的扩展C-树恰好指一棵二叉树T, 其中:①T的根节点N_T满足:G(N_T)⊆G并且V(G(N_T))=V(G), G(N_T)仅包含一个可由LMA算法实现最大化分解的良约束子域G'的复合顶点V'_c; ②若T中任意节点N_F的左子树不为空, 且N_F和该左子树的根节点N_LT满足:G(N_F)⊆G, G(N_LT)⊆G, V(G(N_F))=V(G(N_LT))=V(G), S(G(N_F), G(N_LT))仍然是可由LMA算法实现最大化分解的良约束子域。当该子域与N_F中最多的由复合顶点封装的良约束子域合并构成新的良约束子域G_s时, 由复合顶点封装G_s; 否则, 仅S(G(N_F), G(N_LT))由复合顶点所封装; ③若T中任意节点的右子树不为空, 则该右子树为叶节点N_R, 且N_R为N_T的叶节点时, N_R为G'的广义构造序列; 否则N_R为S(G(N_F), G(N_LT))的广义构造序列。

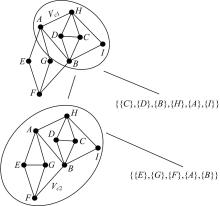
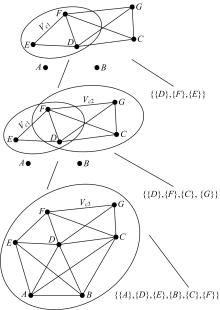
根据上述定义, 扩展C-树是将一个几何约束系统分解为可分别使用LMA算法实现最大化分解的子域的准确描述。因此, 扩展C-树必然是系统的最大化分解树。如:图2和图3分别为图1中几何约束系统的两棵扩展C-树, 其中V_ci为封装良约束子域的复合顶点。可以看出, 两棵C-树均是该几何约束系统的最大化分解。

	Figure Option View Download New Window
	图2 图1所示几何约束系统的扩展C-树1Fig.2 Extension C-Tree of the geometric constraint system showed in Fig.1

	Figure Option View Download New Window
	图3 图1所示几何约束系统的扩展C-树2Fig.3 Extonsion C-Tree of the geometric constraint system showed in Fig.2

2 扩展C-树的构造

由ILMA算法构造扩展C-树的核心思想是:首先, 将几何约束图G的顶点集V(G)作为扩展C-树的根节点N_T; 其次, 对于包括N_T在内的每一个左叶节点N_L_i, 增量地向N_L_i装配G的边并关联与G相对应的顶点, 每装配一条边e_i时, 以e_i关联的顶点为初始子序列在其连通域内执行LMA算法, 并将包括算法获得的增量良约束子域在内的最大基本簇的广义构造序列作为N_L_i右叶节点; 同时, 由复合顶点封装包括算法获得的广义构造序列子域在内的最大基本簇; 最后, 复制N_L_i作为N_L_i的左叶节点, 并以同样方式构造该左叶节点的子节点, 直至所有几何约束边装配完毕。

算法2 搜索包含良约束子域G_ws的最大簇G_MC

步骤1 将G_ws赋值给G_MC, 置G_MC中所有顶点的访问标记为未访问;

步骤2 访问G_MC中尚未访问的顶点v_i。遍历v_i连接的顶点v_j, 如果v_j∉G_MC并且v_j关联的一组边E'满足:E'的任意一条边也关联G_MC的顶点, 同时∑ _e_∈_E'DOC(e)=DOF(v_j), 则加入v_j和E'到G_MC, 置v_j的访问标记为未访问。置v_i的访问标记为已访问。

步骤3 若G_MC中仍包含尚未访问的顶点, 则转步骤2; 否则, 算法终止。

定义10 若复合顶点V_c或子几何约束图G_s的几何基元顶点v连接V_c或G_s外的几何基元顶点, 则称v为V_c或G_s的边缘顶点。

定义11 子约束图G_s=(v₁, e₁₂, v₂, e₂₃, …, v_n-₁, e_n-_1,_n, v_n)称为约束链。其中v_i和e_i_,_i+₁分别为几何基元顶点和几何约束边。

定义12 在几何约束图G中, 如果良约束域G_w⊆G满足:G_w⊄G'_w, 其中G'_w⊆G为任意一个不等于G_w的良约束域, 则称G_w为G的饱和良约束域。

定理1 当在一个右叶节点装配边e_i时, 从e_i关联的顶点执行LMA算法获得的广义构造序列GC中, 由包含于复合顶点的边缘顶点以及复合顶点外的顶点的导出子图必为增量良约束子域。

证明装配e_i前, 由复合顶点封装的子域必为饱和良约束域。假设:使用复合顶点封装GC的子域G_w之前G_w-e_i中由复合顶点封装的所有良约束子域为G_w₁, G_w₂, …, G_wn, 则G_sr=S(…(S(S(G_w-e_i, G_w₁), G_w₂), …), G_wn)为欠约束子域, G_sr∪ e_i为良约束子域且不包含 $\begin{matrix} {G_{w}}_{i} \end{matrix}$ (i=1, 2, …, n)的非边缘顶点。因此, 定理成立。

算法3 搜索增量良约束子域的广义构造序列GC'

步骤1 置GC'为空集;

步骤2 按照GC中的元素顺序访问GC_i, 遍历GC_i的每一个几何基元顶点v_i, 如果v_i是包含于复合顶点的边缘顶点, 则加入v_i到GC'_i;

步骤3 如果GC中仍包含未访问元素, 则转步骤2; 否则, 算法终止。

获得最大簇G_MC后, 可按算法2中几何基元顶点增加的顺序在增量良约束子域的广义构造序列中依次增加相应的几何基元顶点, 从而获得G_MC的广义构造序列。构造扩展C-树的算法如下所示。

算法4 构造扩展C-树T

步骤1 将几何约束图G的顶点集V(G)作为T的根节点N_T;

步骤2 对包括N_T在内的左叶节点N_L, 以增量方式装配一条边e_i, 使e_i关联G中对应的几何基元顶点;

步骤3 访问不被复合顶点封装且包含e_i的最小欠约束链G_L_j, 以G_L_j为初始子域在其连通域内执行LMA算法, 若获得的广义构造序列G_Cj不为空集, 则调用算法2由G获得该子域的最大簇G_MCj;

步骤4 装配边集E(G_MCj)-E(Gj)到N_L, 其中G_j为G_Cj的约束域;

步骤5 按照算法2中几何基元顶点的增加顺序在GC'中依次增加相应的顶点, 获得G_MCj的广义构造序列GC_HCj。

步骤6 调用算法3获得G_MCj中增量良约束子域的广义构造序列GC'_MCj;

步骤7 将GC_MC作为N_L右叶节点;

步骤8 删除封装GCj子域内良约束子域的复合顶点标记, 使用新的复合顶点封装G_MCj;

步骤9 如果仍存在不被复合顶点封装且包含e_i的最小欠约束链G_L_j, 则转步骤3;

步骤10 如果N_L的几何约束图恰好是图G, 则扩展C-树构造完成, 算法终止; 否则, 复制N_L作为N_L的左叶节点, 转步骤2。

若由算法4生成一颗扩展C-树, 则可按照树的右叶节点的生成顺序构成几何约束系统的求解序列, 如:图2中, 广义构造序列{{A}, {E}, {G}, {F}, {B}}的子域被首先求解。其次, {{C}, {D}{A}, {B}, {H}, {I}}的子域被求解。使用坐标系的旋转及平移变换矩阵合并两个子域的解获得原有几何约束系统的解。图3中, 求解按照{{B}, {C}, {D}, {H}, {A}}、{{B}, {H}, {I}}和{{E}, {G}, {F}, {A}, {B}}的生成顺序进行。使用包含装配边e_i的最小欠约束链作为LMA算法初始子域的主要原因是:能够使LMA算法获得所有的包含e_i子域的广义构造序列。

3 系统分解实例

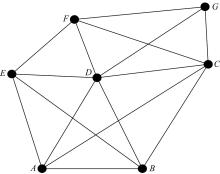
实例1 图4为由点和距离约束构成的三维几何约束图G。若使用文献[17]中的C-树分解法构造C-树, 则必须以A-E的导出子图中三角形结构的子域作为LMA算法的初始子序列, 可获得最大化分解的C-树。此时, 一棵C-树包含的广义构造序列为{{A}, {B}, {C}, {D}, {E}, {F}, {G}}; 否则C-树均不是系统的最大化分解。

	Figure Option View Download New Window
	图4 实例1的几何约束图Fig.4 The geometric constraint graph of example 1

采用本文算法构造扩展C-树, 假设边的增量装配顺序为:(E, F) (C, F) (C, D) (D, E) (D, F) (A, D)。其中, 当装配到边(D, F)时, 根节点N_T中包含(D, F)的最小欠约束链为图G_L1=(D, (D, F), F, (F, E), E)和图G_L2=(D, (D, F), F, (F, C), C), 分别以G_L1和G_L2为初始子域执行LMA算法, 能够获得广义构造序列分别为GC1={{D}, {F}, {E}}和GC2={{D}, {F}, {C}}; 通过执行算法2, 获得包含GC1和GC2子域的最大簇分别为{D, F, E}和{D, F, C, G}的导出子图G_MC₁和G_MC₂; 再执行算法3, 获得增量良约束子域的广义构造序列分别为GC1'=GC1和GC2'={{D}, {F}, {C}, {G}}; 当装配到边(A, D)时, 左叶节点N_L中包含(A, D)的最小欠约束链为图G_L3=(A, (A, D), D, (D, E), E)和图G_L4=(A, (A, D), D, (D, C), C), 以图G_L3为初始子域执行LMA算法, 可获得广义构造序列GC3={{A}, {D}, {E}}, 由算法2获得包含GC3子域的最大簇为{A, D, E, B, C, F, G}的导出子图G_MC₃; 再执行算法3, 获得增量良约束子域的广义构造序列仍为GC3'={{A}, {D}, {E}, {B}, {C}, {F}}。由于图G_L₄被复合顶点分装, 即G_L₄包含于G_MC₃, 因此不必对G_L₄再做处理。所构造的扩展C-树如图5所示。

	Figure Option View Download New Window
	图5 实例1的扩展C-树Fig.5 An extension C-Tree of example 1

	Figure Option View Download New Window
	图6 实例2的几何约束图Fig.6 The geometric constraint graph of example 1

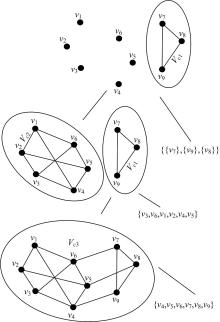
实例2 如图6所示, 为满足DOF(v_i)=2, DOC(e_i)=1的二维几何约束图。其中, e_i为任意两几何基元顶点间的几何约束边。

若采用文献^[17]的方法构造该实例的一棵C-树, 方法是以三角形结构的子系统作为LMA算法的初始子域, 因此不能获得最大化分解的C-树。采用本文算法时, 假设增量装配几何约束边的顺序为(v₇, v₈) (v₉, v₈) (v₇, v₉) (v₁, v₂) (v₂, v₃) (v₃, v₄) (v₄, v₅) (v₅, v₆) (v₆, v₁) (v₁, v₄) (v₂, v₅) (v₃, v₆) (v₆, v₇) (v₅, v₈) (v₄, v₉)。当装配到(v₇, v₉)时, 根节点N_T中包含(v₇, v₉)的最小欠约束链为图G_L1=(v₇, (v₇, v₉), v₉, (v₉, v₈), v₈), 以G_L1作为初始子域时, 能够获得LMA算法的广义构造序列为GC1={{v₇}, {v₉}, {v₈}}, 由算法2和算法3可获得增量良约束子域的广义构造序列仍然为GC1'=GC1本身; 当装配到(v₃, v₆)时, 左叶节点N_L中包含(v₃, v₆)的最小欠约束链为图G_L₂=(v₃, (v₃, v₆), v₆, (v₆, v₁), v₁)和G_L₃=(v₃, (v₃, v₆), v₆, (v₆, v₅), v₅), 以G_L₂作为初始子域执行LMA算法后, 可获得广义构造序列GC2={v₃, v₆, v₁, v₂, v₄, v₅}, 再由算法2和算法3仍可获得增量良约束子域的广义构造序列为GC2'=GC2本身; 同样, 因此时G_L₃已被复合顶点封装, 所以不对G_L₃做任何处理; 最后, 装配到(v₄, v₉)时, 可获得以最小欠约束链G_L₄=(v₄, (v₄, v₉), v₉, (v₄, v₁), v₁)为初始子域的LMA算法的广义构造序列GC3={v₄, v₉, v₁, v₂, v₃, v₅, v₆, v₇, v₈}, 通过算法2获得包含GC3子域的最大簇仍为GC3本身, 再由算法3获得增量良约束子域的广义构造序列GC3'={v₄, v₅, v₆, v₇, v₈, v₉}。扩展C-树如图7所示, 为最大化分解。

	Figure Option View Download New Window
	图7 实例2的扩展C-树Fig.7 An extension C-Tree of example 2

4 结束语

本文提了几何约束求解的扩展C-树分解法, 基于增量LMA(ILMA)算法将几何约束系统分解为一棵扩展C-树。该方法增量地装配边到几何基元顶点集, 并以包含装配边的最小欠约束链为初始子域执行LMA算法, 搜索LMA算法的广义构造序列中由除复合顶点的非边缘顶点组成的增量良约束子域的广义构造序列, 该序列是增量良约束子域的最大化分解序列。当以任意方式装配边时, 该方法均能够保证所构造的扩展C-树必是几何约束系统的最大化分解。最后, 通过实例证明了本文方法的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	He Chun-hua, Zhang Xiang-wei, Lv Wen-ge. A new approach for solving geometric constraint based on Election-Survey Algorithm[C]//International Conference on Computer, Mechatronics, Control and Electronic Engineering (CMCE), Changchun, China, 2010Hong Kong: IITA Association, 2012: 427-430. [本文引用:1]
[2]	Cao Chun-hong, Zhang Bin, Li Wen-hui. The research based on the composite particle swarm optimization algorithm in the geometric constraint solving[J]. Journal of Image and Graphics, 2007, 12(4): 713-717. [本文引用:1]
[3]	Cao Chun-hong, Tang Chuan, Zhao Da-zhe, et al. Geometric constraint solving based on geese PSO optimization[J]. Journal of Chinese Computer System, 2011, 32(11): 2299-2302. [本文引用:1]
[4]	Kondo K. Algebraic method for manipulation of dimensional relationships in geometric models[J]. Computer-Aided Design, 1992, 24(3): 141-147. [本文引用:1]
[5]	Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Journal on Computing, 1997, 26(5): 1484-1509. [本文引用:1]
[6]	Lin Qiang, Gao Xiao-shan, Liu Yuan-yuan. The complete method based on geometric constraint solving[J]. Journal of Computer- Aided Design & Computer Graphics, 2007, 19(7): 828-834. [本文引用:1]
[7]	Owen J. Algebraic solution for geometry from dimensional constra- ints[C]//Proceedings of ACM Symposiumon Solid Modeling Foundation, Austin, TX, 1991, 397-407. [本文引用:1]
[8]	Owen J. Constraints of simple geometry in two and three dimensions[J]. Intemational Journal of Computer Geometry and Its Applieations, 1996, 6(5): 421-423. [本文引用:1]
[9]	Fudos I, Hoffmann C M. A graph-constructive approach to solving systems of geometric constraints[J]. ACM Transactions on Graphics, 1997, 16(2): 179-216. [本文引用:1]
[10]	Hoffmann C M. Geometric Constraint Solving in R2 and R3[M]. In: Du D Z, Huang F, eds. Computing in Euclidean Geometry. Singapore: World Scientific, 1995. 266-298. [本文引用:1]
[11]	Hoffmann C M, Lomonosov A, Sitharam M. Finding solvable subsets of constraint graphs[C]//Principles and Practice of Constraint Programming-CP97, Third International Conference, Linz, Austria, 1997: 463-477. [本文引用:1]
[12]	Hoffmann C M, Lomonosov A, Sitharam M. Decomposition plans for geometric constraint systems: I[J]. Performance measures for CAD. J Symbolic Comput 2001; 31: 367-408. [本文引用:1]
[13]	Hoffmann C M, Lomonosov A, Sitharam M. Decomposition plans for geometric cons- traint systems. II[J]. New algorithms. J Symbolic Comput 2001; 31: 409-427. [本文引用:1]
[14]	Hoffmann C M, Lomonosov Andrew, Sitharam Meera. Decompo-sition plans for geom-etric constraint systems, Part I: Performance measures for CAD[J]. Journal of Symbolic Computation, 2001, 31(4): 367-408. [本文引用:1]
[15]	Samy Ait-Aoudia, Sebti Foufou. A 2D geometric constraint solver using a graph reduction method[J]. Advances in Engineering Software, 2010; 41: 1187-1194. [本文引用:1]
[16]	Latham R S, Middleditch A E. Connectivity analysis: a tool for processing geometric constraints[J]. Computer-Aided Design 1996, 28: 917-928. [本文引用:1]
[17]	Gao X, Lin Q, Zhang G. A C-tree decomposition algorithm for 2D and 3D geometric constraint solving[J]. Computer-Aided Design, 2006; 38(1): 1-13. [本文引用:3]
[18]	Lee J Y, Kwon O-Hwan, Lee Jae-Yeol, et al. A hybrid approach to geometric constr- aint solving with grapg analysis and reduction[J]. Advance in Engineering Software, 2003, 34(2): 103-113. [本文引用:1]

2012

0.0