引用本文
朱叶, 申铉京, 陈海鹏. 基于混合灰度序模式的图像复制-粘贴篡改盲鉴别算法. 2017, 47(4): 1280-1285
ZHU Ye, SHEN Xuan-jing, CHEN Hai-peng. Copy-move forgery detection based on mixed intensity order pattern. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1280-1285  
Permissions
Copyright©2017, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于混合灰度序模式的图像复制-粘贴篡改盲鉴别算法
朱叶1,2, 申铉京1,2, 陈海鹏1,2
1.吉林大学 计算机科学与技术学院,长春 130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012
通讯作者：陈海鹏(1978-),男,副教授,博士.研究方向:图像处理与模式识别,多媒体信息安全.E-mail:chenhp@jlu.edu.cn

作者简介:朱叶(1989-),女,博士研究生.研究方向:图像盲鉴别.E-mail:zhuye13@mails.jlu.edu.cn

基金:国家自然科学基金青年基金项目(61305046, 61602203); 吉林省自然科学基金项目(20140101193JC, 20150101055JC).
摘要

针对目前复制-粘贴篡改盲检测算法对光照变换操作鲁棒性较差的问题,提出了一种基于混合灰度序模式(Mixed Intensity Order Pattern, MIOP)的复制-粘贴篡改盲鉴别算法。首先,对待检测图像提取高斯差分区域(Difference of Gaussians, DOG)。其次,利用MIOP特征描述区域。最后,匹配特征并利用RANSAC (RANdom SAmple Consensus)去除误匹配,确定图像的复制-粘贴篡改区域。实验结果表明:本文算法不仅对几何变换和光照操作的检测率较高,且对高斯模糊、噪声和JPEG重压缩等后处理操作鲁棒性较好。

关键词: 计算机应用; 盲鉴别; 图像复制-粘贴篡改; 光照变换; 混合灰度序模式
中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2017)04-1280-06
Copy-move forgery detection based on mixed intensity order pattern
ZHU Ye1,2, SHEN Xuan-jing1,2, CHEN Hai-peng1,2
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Key Laboratory of Symbol Computation and Knowledge Engineering, Ministry of Education, Jilin University, Changchun 130012, China
Abstract

In order to solve the low robustness of copy-move forgery detection with illumination change, a novel method based on Mixed Intensity Order Pattern (MIOP) was proposed. First, the Difference of Gaussian (DOP) regions of the image to be detected are extracted. Second, the regions are described using MIOP. Third, the features are matched and the false matching is removed by RANdom SAmple Consensus (RANSAC). Finally, the copy-move forgery regions are detected. Experimental results show that the proposed method not only has high accuracy on geometric transformation and illumination change, but also has high robustness on post-processing operations, such as Gaussian blur, noise and JPEG recompression.

Keyword: computer application; blind identification; copy-move forgery; illumination change; mixed intensity order pattern
0 引 言

数字图像作为现代社会的主要信息来源, 其真实性已成为一个重要研究课题。但是, 随着图像处理软件的发展, 图像篡改已经越来越容易。其中, 复制-粘贴作为常见的图像篡改手段, 即复制一个或多个区域, 在进行旋转、缩放、光照变换等操作后粘贴到同幅图像, 以达到增加或掩盖目标的目的。

目前复制-粘贴篡改盲检测算法的基本流程大致可分为3步:①图像重叠分块或特征点提取; ②图像块或特征点进行特征描述; ③特征描述符匹配并滤除误匹配。

基于图像重叠分块的复制-粘贴检测算法, 如离散余弦变换(Discrete cosine transform, DCT)[1], 主成分分析(Principal component analysis, PCA)[2], 傅里叶-梅林变换(Fourier-Mellin transform, FMT)[3], Hu不变矩[4]、blur不变矩[5]、Zernike矩[6]和Dense-Field[7]等, 对区域平滑的篡改图像检测率较高, 旋转和缩放等几何变换鲁棒性较差, 而且对光照变换的复制-粘贴篡改完全束手无策。

基于图像特征点提取的复制-粘贴盲检测算法, 如SIFT[8], SURF[9], Daisy[10], ORB[11]等, 该类算法对旋转和缩放等几何变换检测率较高, 但是对光照变换的鲁棒性较差。

图像特征区域提取不受传感器获取图像时的视角、相机参数变化等的影响, 对旋转、缩放等几何变换有较好的鲁棒性。混合灰度序模式(Mixed intensity order pattern, MIOP)是全局灰度序信息(Overall intensity order pattern, OIOP)和局部灰度序信息(Local intensity order pattern, LIOP)的融合, 在局部特征计算中使用了与方向无关的采样策略, 因此, 具有几何旋转不变性, 并且对光照变换具有较好的鲁棒性[12]。基于此, 本文提出基于高斯差分(Different of Gaussians, DOG)区域[13]和混合灰度序模式的复制-粘贴篡改盲检测算法。

1 算法描述
1.1 图像DOG区域提取

图像区域检测是图像特征提取的重要方式, 即提取图像区域后进行特征描述。由于特征点在其尺度上的自相关矩阵可以近似刻画局部区域形状, 因此, 提取的图像区域具有尺度不变性。

设图像I(x, y)的高斯尺度空间为L(x, y; σ ), σ 为高斯平滑因子(初始 σ=2[13])。本文首先在DOG区域提取多尺度的特征点, 并记为 Pi={xi, yi; σi}。然后计算特征点的自相关矩阵, 则点Pi的椭圆方程系数矩阵C如式(1)所示:

C=G(xi, yi; σi)×Lx2LxLyLxLyLy2(x, y; σi)(1)

式中:σ i 为特征点所在的尺度; Lx 和Ly 分别为尺度空间L(x, y; σ i)在x和y方向上的微分。

1.2 混合灰度序模式特征描述

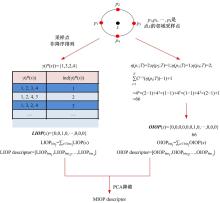
针对复杂光照变化下的复制-粘贴篡改特征较难匹配的问题, 本文采用Fan提出的基于全局灰度序信息OIOP和局部灰度序信息LIOP的混合灰度序模式MIOP特征描述方法[12]。LIOP和OIOP分别描述了特征点局部区域内每个像素点周围采样点的局部和全局灰度序列信息, 则MIOP的融合, 显著的提高了描述子的性能。

首先将图像块按灰度值排序, 并将所有灰度范围划分为 B个区间(Ordinal bin)。然后, 在每个区间内分别提取LIOP和OIOP特征描述符。设bini 区间任意点x, P(x)={p1, p2, …, pn}是点x的邻域采样点。

(1)LIOP特征描述符提取

将P(x)进行非降序排列, γ (P(x))为排列后的索引序列。设数组{1, 2, …, n}全排序是ind, LIOP(x)为第ind(γ (P(x)))个元素为1, 其余元素都为0的n!维的特征向量, 点x的LIOP特征 LIOP(x)如式(2)所示:

LIOP(x)={0, 0, 0, 0, 0, 0, 1ind(γ(P(x))), 0, …0, 0, 0}2

(2)OIOP特征描述符提取

首先将图像块中像素点量化为Q个级别, 设阈值集合T={t1, t2, …, tQ-1}, 则:

η(pi; T)=1, I(pi)≤t1k, tk-1< I(pi)≤tk, k=2, 3, …, Q-1Q, I(pi)> tQ-13

式中:I(Pi)为采样点Pi的灰度值。

OIOP(x)为第 ∑i=1nCi-1(η (pi; T)-1)+1个元素为1, 其余元素都为0的 Cn维的特征向量, 点 x的OIOP特征 OIOP(x)如式(4)所示:

OIOP(x)={0, 0, 0, 0, 0, 0, 1∑i=1nCi-1(η(pi; T)-1)+1, 0, …0, 0, 0}(4)

(3)MIOP的特征描述符提取

MIOP特征是LIOP和OIOP特征的融合, LIOP的特征维数为 n!×B, OIOP的特征维数为 Qn×B, 则MIOP的特征维数为n!× B+Qn× B。设B=4, Q=4, n=4时, MIOP的维数为1120。由于直接串联得到的MIOP维度过高, 则采用主成分分析方法进行降维到128, 并标记为MIOPi 。设Q=4, n=4时的MIOP特征提取流程如图1所示。

图1 MIOP特征描述流程(Q=4, n=4)Fig.1 The framework of MIOP description(Q=4, n=4)

1.3 篡改区域定位

特征匹配中, 欧几里德距离常用来描述特征的相似性。设DOG区域 i和j的MIOP特征MIOPi 和MIOPj 的欧几里得距离标记为dis(i, j), 则若满足式(5), 则DOG区域i和j为匹配区域。

disi, j/disi, n< th, 1< n< N5

式中: N表示DOG区域的个数。最后, 利用RANSAC算法[14]去除误匹配, 定位复制-粘贴篡改区域。

2 实验分析

由于目前复制-粘贴图像库中不包含光照变换篡改操作, 本文选择Amerini提出的MICC-F2000图像库[8]中100幅原始真实图像和100幅复制-粘贴篡改图像, 并添加粘贴区域的光照变换篡改操作。本实验的硬件环境为:主频2.60 GHz, Intel Celeron E3400处理器, 3 G内存; 软件环境为:Windows 7+Matlab R2012b+Visual Studio 2015+Opencv 3.0.0。

2.1 算法度量

为了综合性地度量算法, 本文使用Cozzolino采用F1-measure[7], 如式(6)所示:

F1=2TP2TP+FN+FP6

式中:TP(True positive)是被正确检测为篡改图像的数目; FP(False positive)是被检测为篡改图像的真实图像的数目; FN(False negative)为被检测为真实图像的篡改图像的数目。F1值越大, 算法性能越好。

2.2 算法实验结果

2.2.1 光照变换篡改实验

(1)线性光照变换

该节对图像库中篡改图像的粘贴区域分别添加两组不同程度的线性平行光, 生成200幅光照线性变换的篡改图像。Dense-Field[7], SIFT[8]和本文算法检测结果示例如图2(a~d)所示。

(2)非线性光照变换

该节对图像库中篡改图像的粘贴区域添加不同程度的非线性点光源, 生成100幅光照线性变换的篡改图像。Dense-Field[7], SIFT[8]和本文算法检测结果示例如图2(e~f)所示。

由图2实验结果可知, 本文算法较SIFT[8]能更精确地匹配复制-粘贴篡改区域, 而Dense-Field[7]则完全不能定位篡改区域。

2.2.2 几何变换篡改实验

该节对图像库中篡改图像的粘贴区域进行不同大小的旋转和尺度变换, 共生成200+200幅几何变换的篡改图像。Dense-Field[7], SIFT[8]和本文算法检测结果示例如图3所示。

图2 光照变换复制-粘贴篡改结果示例Fig.2 Exemplar results on illumination change of copy-move forgery

图3 几何变换复制-粘贴篡改结果示例Fig.3 Exemplar results on geometric transformation of copy-move forgery

由实验结果可知, 本文算法, SIFT[8]和Dense-Field[7]在简单平移的复制-粘贴篡改中都表现较好, 在篡改区域旋转和尺度变换后, 本文算法更能匹配正确的特征点, SIFT[8]特征点匹配明显减少, 而Dense-Field[7]在尺度变换性能较差。

2.2.3 光照和几何变换混合篡改实验

为了综合验证本文算法性能, 该节对图像库中篡改图像的粘贴区域进行混合操作, 共生成200幅混合操作篡改图像。Dense-Field[7], SIFT[8]和本文算法检测结果示例如图4所示。

图4 混合操作复制-粘贴篡改结果示例Fig.4 Exemplar results on mixed operation of copy-move forgery

由实验结果可知, SIFT[8]匹配的特征点过少, Dense-Field[7]在光照变换的条件下完全束手无策, 只有本文算法能准确定位复制-粘贴篡改区域。

2.2.4 后处理操作鲁棒性实验

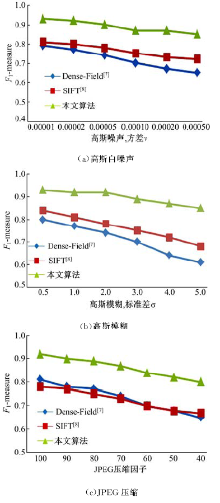
图像在传输过程中受到噪声、模糊、压缩等后处理操作影响, 增加了复制-粘贴算法的难度。因此, 检测算法对后处理操作的鲁棒性, 是衡量其性能的重要指标。

本节对数据库中图像分别添加:①高斯白噪声:利用Matlab函数imnoise, 其参数设为均值m=0, 方差v=[0.00001, 0.00002, 0.00005, 0.0001, 0.0002, 0.0005]; ②高斯模糊:利用Matlab函数imfilter添加与高斯模糊, 其窗口尺寸w=3, 标准差σ =[0.5, 1, 2, 3, 4, 5]; ③JPEG压缩:压缩因子从100至40, 以-10为间隔。Dense-Field[7], SIFT[8]和本文算法F1-measure曲线如图5所示。

图5 后处理操作F1-measure曲线图
F1-measure Curves on different post-processing

2.2.5 算法有效性实验

为了验证算法针对纹理信息丰富, 篡改区域与周围背景差异不明显的复制-粘贴篡改的有效性, 本节选择MICC-F2000图像库[8]中10幅真实和其篡改图像进行实验。本文算法检测结果示例如图6所示。

图6 纹理丰富的复制-粘贴篡改结果示例Fig.6 Exemplar results on rich texture copy-move forgery

3 结束语

针对目前复制-粘贴篡改盲检测算法对光照变换操作鲁棒性较差的问题, 本文提出了一种基于DOG区域和MIOP的复制-粘贴盲鉴别算法。通过实验证明, 本文算法与Dense-Field[7], SIFT[8]相比, 不仅对几何和光照变换的篡改图像检测率较高, 并对模糊、噪声和JPEG重压缩等后处理操作有较好的鲁棒性。

The authors have declared that no competing interests exist.

参考文献
[1] Fridrich A J, Soukal B D, Lukáš A J. Detection of copy-move forgery in digital images[C]//Proc of Digital Forensic Research Workshop, 2003. [本文引用:1]
[2] Popescu A C, Farid H. Exposing digital forgeries by detecting duplicated image regions[R]. TR 2004-515, Dartmouth College, 2004. [本文引用:1]
[3] Bayram S, Sencar H T, Memon N. An efficient and robust method for detecting copy-move forgery[C]//Proc of the 2009 IEEE Int Conf on Acoustics, Speech and Signal Processing. Piscataway, NJ, 2009: 1053-1056. [本文引用:1]
[4] Liu Guang-jie, Wang Jun-wen, Lian Shi-guo, et al. A Passive image authentication scheme for detecting region-duplication forgery with rotation[J]. Journal of Network and Computer Applications, 2011, 34(5): 1557-1565. [本文引用:1]
[5] Mahdian B, Saic S. Detection of copy-move forgery using a method based on blur moment invariants[J]. Forensic Science International, 2007, 171(2): 180-189. [本文引用:1]
[6] Ryu S J, Kirchner M, Lee M J, et al. Rotation invariant localization of duplicated image regions based on Zernike moments[J]. IEEE Transactions on Information Forensics and Security, 2013, 8(8): 1355-1370. [本文引用:1]
[7] Cozzolino D, Poggi G, Verdoliva L. Efficient dense-field copy-move forgery detection[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(11): 2284-2297. [本文引用:12]
[8] Amerini I, Ballan L, Caldelli R, et al. A sift-based forensic method for copy-move attack detection and transformation recovery[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(3): 1099-1110. [本文引用:13]
[9] Bo X, Junwen W, Guangjie L, et al. Image copy-move forgery detection based on SURF[C]//International Conference on Multimedia Information Networking and Security(MINES), 2010: 889-892. [本文引用:1]
[10] Guo J M, Liu Y F, Wu Z J. Duplication forgery detection using improved DAISY descriptor[J]. Expert Systems with Applications, 2013, 40(2): 707-714. [本文引用:1]
[11] Zhu Ye, Shen Xuan-jing, Chen Hai-peng. Copy-move forgery detection based on scaled ORB[J]. Multimedia Tools and Applications, 2016, 75(6): 3221-3233. [本文引用:1]
[12] Wang Zhen-hua, Fan Bin, Wang Gang, et al. Exploring local and overall ordinal information for robust feature description[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence (TPAMI), 2016, 38(1): 2698-2211. [本文引用:2]
[13] Lowe G D. Object recognition from local scale-invariant features[J]. Proceeding of the International Conference on Computer Vision (ICCV), 1999, 2: 1150-1157. [本文引用:2]
[14] Fischler M A, Bolles R C. Rand om sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. [本文引用:1]