基于移位协方差矩阵Otsu算法的信源数目估计

引用本文

关济实, 石要武, 单泽彪, 石屹然, 史红伟. 基于移位协方差矩阵Otsu算法的信源数目估计. 2017, 47(4): 1295-1300
GUAN Ji-shi, SHI Yao-wu, SHAN Ze-biao, SHI Yi-ran, SHI Hong-wei. Estimation of number of signals based on Otsu class variance with shift covariance matrix. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1295-1300 复制到剪切板

Permissions

基于移位协方差矩阵Otsu算法的信源数目估计

关济实^1,², 石要武¹, 单泽彪^1,³, 石屹然¹, 史红伟³

1.吉林大学通信工程学院,长春 130022

2.中广核研究院有限公司北京分公司, 北京 100086

3.长春理工大学电子信息工程学院, 长春 130022

通讯作者：单泽彪(1986-),男,讲师,博士.研究方向:雷达与阵列信号处理.E-mail:zbshan@126.com

作者简介:关济实(1977-),男,博士研究生.研究方向:阵列信号处理.E-mail:guanjishi@sina.com

基金:国家自然科学基金项目(61571462); 国防基础科研计划项目(JCKY2016411C006).

摘要

针对阵列信号处理中信号源数目估计的问题,提出了一种基于移位协方差矩阵的Otsu类间方差法。与协方差矩阵相比,移位协方差矩阵克服了噪声自相关过程中零位极大值的影响,提高了协方差矩阵的信噪比,移位协方差矩阵的信号特征值与噪声特征值差别更为明确,更有利于信源数目的估计。由于零均值且独立同分布噪声的移位协方差理论值为0,所以移位协方差矩阵针对零均值独立同分布 α稳定分布噪声同样具有较强的抑制能力。利用Otsu类间方差法对移位协方差矩阵的特征值进行分类,可以更加明确地区分信号特征值与噪声特征值。理论分析和仿真实验结果均表明,基于移位协方差矩阵的Otsu类间方差法具有比传统信源数估计方法更好的估计性能。

关键词: 信息处理技术; 信源数目估计; 移位协方差矩阵; Otsu类间方差法

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2017)04-1295-06

Estimation of number of signals based on Otsu class variance with shift covariance matrix

GUAN Ji-shi^1,², SHI Yao-wu¹, SHAN Ze-biao^1,³, SHI Yi-ran¹, SHI Hong-wei³

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.Beijing Branch, China Nuclear Power Technology Research Institute, Beijing 100086,China

3.School of Electric and Information Engineering, Changchun University of Science and Technology, Changchun 130022,China

Abstract

An estimation of the number of signals based on Otsu class variance with shift covariance matrix is proposed for array signal processing. The eigenvalues of the shift covariance matrix derived by noise are expected to be zero even with stable noise, so the eigenvalues derived by signal power are obviously smaller than those derived by noise, which is an advantage for signal number estimation. When class variance, which is used for classification in many problems, is applied to estimate the signal number, Otsu class variance can efficiently distinguish the eigenvalues derived by noise and by signal power. Combining the shift covariance matrix and Otsu class variance, an efficient method is obtained to estimate the signal number in array signal processing. Theoretical analysis and simulation experiments show that the performance of the proposed method is better than that of traditional method.

Keyword: information processing; source number estimation; shift covariance matrix; Otsu class variance method

Show Figures

0 引言

阵列信号处理是将一组传感器按一定方式布置在空间的不同位置上, 形成传感器阵列, 用传感器阵列来接收空间信号, 其在通信、雷达、声纳和地震勘探等领域有着广泛的应用^{[1, 2, 3]}。在阵列信号处理中, 空间可以有多个信号源, 传感器阵列接收到信号源发出的信号后, 根据信号在阵列不同阵元上所得到的响应不同, 可以感知信号源的数目、波达方向或频率等信息。子空间类的MUSIC^[4]和ESPRIT^[5]系列算法因具有超分辨能力而得到了广泛的关注和研究。这一类算法中, 一般要求空间信号源数目已知^{[6, 7, 8]}, 进而为信号子空间和噪声子空间的分离提供支持, 所以对空间信号源数目的准确估计是这一类算法进行波达方向等参数估计的前提。

现有的信源数目估计方法包括特征值分解方法、信息论方法、盖氏圆方法和正则相关方法等^[9], 这些方法均是针对高斯噪声下的信源数目估计问题而提出的, 都是基于“ 信号协方差矩阵的特征值可以分为信号特征值与噪声特征值, 而且信号特征值要大于噪声特征值” 这一特征来进行信号源数目的估计。但当信噪比较低时, 代表信号的特征值与代表噪声的特征值之间相差很小, 这些方法估计信源数目时会出现误差, 从而对后续参数估计产生较大的影响。

本文提出移位协方差矩阵的概念及其特征值分布的特征, 进而提出用Otsu类间方差法^[10]进行信源数目估计的方法。移位协方差矩阵可以提高信号特征值与噪声特征值之间的差距, 而Otsu方法则使用模式识别中的分类准则对特征值进行分类, 进一步提高信源数目估计的准确度。仿真实验表明, 移位协方差矩阵的信号特征值与噪声特征值之比远大于原来协方差矩阵, 而且Otsu类间方差方法的信源数目估计性能也同样优于现有的信源数目估计方法, 即使在非高斯的α 稳定分布^[11]噪声下, 本文方法同样具有良好的性能。

1 信号模型

设定阵列为均匀线阵, 其中阵元数为N, 并假设空间有P(P< N)个来自不同方位角(θ ₁, θ ₂, …, θ _P)的目标源信号, 信号的中心频率为f, 则第n个阵元的接收信号为:

$\begin{matrix} x_{n} (t) = \overset{P}{\sum_{p = 1}} s_{p} (t) e^{- j 2 πf τ_{n} (θ_{p})} + g_{n} (t) (1) \end{matrix}$

式中:s_p(t)表示第p个源信号; τ _n(θ _p)表示方位角为θ _p的信号到达该阵元时相对参考阵元的时延; g_n(t)表示加性零均值独立同分布观测噪声。

整个阵列的接收信号可表示为如下矩阵形式:

$X (t) = AS (t) + G (t) (2)$

其中：

$\begin{matrix} X (t) & = {[x_{1} (t), x_{2} (t), \dots, x_{N} (t)]}^{T} (3) \\ S (t) & = {[s_{1} (t), s_{2} (t), \dots, s_{P} (t)]}^{T} (4) \\ G (t) & = {[g_{1} (t), g_{2} (t), \dots, g_{N} (t)]}^{T} (5) \\ A & = [a (θ_{1}), a (θ_{2}), \dots, a (θ_{P})] (6) \end{matrix}$

式中:上标T表示转置运算符; a(θ _p)(p=1, 2, …, P)表示第p个信号的导向矢量。

求取X(t)的协方差矩阵R, 有

$\begin{matrix} \begin{matrix} R = E [X (t) X^{H} (t)] = \\ E [AS (t) S^{H} (t) A] + E [AS (t) G^{H} (t)] + \\ E [G (t) S^{H} (t) A] + E [G (t) G^{H} (t)] (7) \end{matrix} \end{matrix}$

式中:上标H表示共轭转置运算符; 中间两项为信号与噪声的互相关矩阵, 在信号与噪声独立及噪声零均值的假设下, 二者均为0; 最后一项为噪声向量G(t)的自相关矩阵, 所以有:

$\begin{matrix} E [G (t) G^{H} (t)] = σ^{2} I (8) \end{matrix}$

式中:σ ²表示噪声功率; I表示单位阵。因此, 式(7)又可写为:

$\begin{matrix} R = AE [S (t) S^{H} (t)] A^{H} + σ^{2} I (9) \end{matrix}$

对协方差矩阵R进行特征值分解, 可得:

$\begin{matrix} R = UΣ U^{H} = \overset{N}{\sum_{n = 1}} λ_{n} u_{n} {u^{H}}_{n} (10) \end{matrix}$

式中:Σ 为由特征值λ _n(n=1, 2, …, N)组成的对角阵; U为由正交特征向量u_n(n=1, 2, …, N)组成的酉矩阵。可以证明得到特征值服从以下排序^[8]:λ ₁≥ λ ₂≥ …≥ λ _P≥ λ _P+₁=…=λ _N=σ ²。由于较小的特征值对应噪声功率, 当噪声功率较小时, 大特征值与小特征值之间可以明确区分, 进而可以根据较大特征值的数量得到信源数目的估计, 这便是特征值分解法估计信源数目的基础^[9]。

2 移位协方差矩阵的定义及性质

由于协方差矩阵的对角线元素受到噪声的影响较为严重, 这一点也影响了协方差矩阵的特征分解过程, 所以在信噪比较低时信号特征值与噪声特征值不易区分, 进而导致信源数目估计的失败。基于这一认知并假定噪声服从独立同分布这一前提, 本文提出移位协方差矩阵(Shift covariance matrix, SCM)的定义, 分析了SCM的性质, 进而根据SCM进行信源数目估计的研究。

定义阵列信号的移位协方差矩阵为:

$\begin{matrix} R_{ε} = E [X (t) X^{H} (t - ε)] (11) \end{matrix}$

式中:ε (0< ε < 1/f)为一特定的时间延迟。

SCM的元素为两个阵列输出的相关函数在ε 处的值。显然, 当ε =0时, 移位协方差矩阵就恢复为传统协方差矩阵R。

遵循第1节中的信号模型, 下面分析移位协方差矩阵的特性。

$\begin{matrix} \begin{matrix} R_{ε} = E [X (t) X^{H} (t - ε)] = \\ E [AS (t) S^{H} (t - ε) A^{H}] + E [AS (t) G^{H} (t - ε)] + \\ E [G (t) S^{H} (t - ε) A^{H}] + E [G (t) G^{H} (t - ε)] (12) \end{matrix} \end{matrix}$

式中:由于信号与噪声相互独立, 所以中间两项仍为0, 而噪声为零均值且独立同分布, 所以最后一项同样为0。又由于信号为窄带信号, 时间延迟ε (0< ε < 1/f)前后信号包络基本不变, 仅相当于信号发生了纯相移e^j2π^fε, 所以移位协方差矩阵R_ε可表示为:

$\begin{matrix} \begin{matrix} R_{ε} = E [AS (t) S^{H} (t - ε) A^{H}] = \\ E \{AS (t) {[S (t) e^{- j 2 πfε}]}^{H} A^{H}\} = \\ e^{j 2 πfε} AE [S (t) S^{H} (t)] A^{H} (13) \end{matrix} \end{matrix}$

观测式(13)可以发现R_ε不再是H矩阵, 因为 $\begin{matrix} {R^{H}}_{ε} \end{matrix}$ =e^-j2π^fεAE[S(t)S^H(t)]A^H=e^-j4π^fεR_ε。对比移位协方差矩阵R_ε和协方差矩阵R, 可以看到, 除了有无噪声项外, 二者仅相差一个相位系数e^j2π^fε, 这个相位系数中信号频率f已知, ε 为求取时设定值, 也为已知, 所以这个相位系数是已知的。将移位协方差矩阵整体除以这个相位系数, 则可以得到移位协方差矩阵的另一种表达形式:

$\begin{matrix} R_{SCM} = e^{- j 2 πfε} R_{ε} = AE [S (t) S^{H} (t)] A^{H} (14) \end{matrix}$

由这种方式得到的协方差矩阵, 称为移位协方差矩阵, 即SCM, 以区别于直接协方差矩阵(Direct covariance matrix, DCM)。

对R_SCM进行特征值分解, 得到:

$\begin{matrix} R_{SCM} = \overset{N}{\sum_{n = 1}} β_{n} v_{n} {v^{H}}_{n} (15) \end{matrix}$

式中:v_n(n=1, 2, …, N)为正交特征向量; β _n(n=1, 2, …, N)为特征值, 且有如下关系:β ₁≥ β ₂≥ …≥ β _P≥ β _P+₁=…=β _N=0, 其中P个非零特征值的数量就是所估计的信源数目。

SCM中噪声对于所有元素的影响都会比较小, 而不只是仅对对角线元素施加比较大的影响。从定义中可以看出, SCM与DCM特性相同, 只是求取方法不同, 所以DCM所具有的性质, SCM也都具备。同时, SCM具备更高的信噪比, 即在SCM中, 信号特征值与噪声特征值之间的比值显著增大, 这是因为SCM中没有了DCM中的σ ²I这一项, 理论上噪声项形成的特征值趋于0。这一特征在特征值的分布情况中表现得尤为明显。值得注意的是, 以上讨论中对于噪声的限定为零均值且服从独立同分布, 并未规定噪声的二阶矩是否有限, 也没有规定噪声为高斯噪声, 所以上述性质对于零均值服从独立同分布的非高斯α 稳定分布噪声也同样成立。

在实际系统中, 应用的是移位采样协方差矩阵 $\begin{matrix} {\hat{R}}_{SC M} \end{matrix}$ , 即:

$\begin{matrix} {\hat{\hat{R}}}_{SCM} = e^{- j 2 πfn} \frac{1}{L} \overset{L}{\sum_{l = 1}} X (l) X^{H} (l - n) (16) \end{matrix}$

式中:L为采样快拍数; n表示延迟序列数。从式(13)(14)中可以看到ε (0< ε < 1/f)的取值不同, 并不会影响移位协方差矩阵R_SCM。

根据奈奎斯特采样定理有:

$\begin{matrix} f_{s} \geq 2 cf (17) \end{matrix}$

式中:f_s为采样频率; c∈ [1, ¥ ]表示采样频率系数。

同时根据窄带信号的定义可知频率与带宽B的关系为^[9]:

$\begin{matrix} B / f < 1 / 10 (18) \end{matrix}$

联合式(17)(18)可得到下式:

$\begin{matrix} n / f_{s} \leq 2 c / f_{s} \leq 1 / f < 1 / (10 B) (19) \end{matrix}$

则得到n的取值范围为:

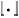
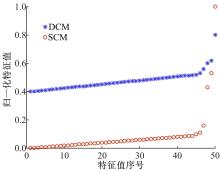
式中: 表示向下取整运算符。所以只要符合式(20)的延迟序列n均可以选取应用, 且所得结果一致。因此在本文后续的仿真实验中, 为计算方便, 取其等于一个快拍周期, 即n=1。

下面给出一个仿真实验, 实验条件为:均匀线阵; 50个阵元; 快拍数为1000; 空间有3个信号源; 噪声为高斯白噪声。在SNR为-15 dB时应用SCM和DCM的特征值分布情况如图1所示。

	Figure Option View Download New Window
	图1 DCM和SCM的特征值分布Fig.1 Eigenvalue distribution via DCE and SCM

从图1可以看出, 在SNR=-15 dB时, DCM的信号特征值与噪声特征值之间已经无法明确分辨, 而SCM的信号特征值与噪声特征值仍具有较为明确的区分。由此可知, SCM与DCM有着相同的特性, 而SCM的噪声抑制能力要高于DCM, 所以SCM可以用来提高信源数等参数估计的性能。

3 基于移位协方差矩阵的信源数目估计

由上所述, SCM的性质与DCM的完全相同, 所以现有的基于DCM的方法均可以应用于SCM。下面分别以特征值分解方法^[9]、盖氏圆法^[9]和Otsu类间方差法为例, 采用蒙特卡罗仿真实验的方法, 分别对DCM和SCM执行这3种算法, 以比较其性能。以下实验中均假设空间有4个目标, 即信源数目为4; 阵元数为50; 应用均匀线阵并且快拍数设为1000。噪声分别取高斯噪声和独立同分布α 稳定分布噪声(特征指数α =1.8), 根据不同情况, 取若干信噪比点, 进行1000次蒙特卡罗实验, 统计正确估计信源数目的比例, 绘制算法性能图。

需要特别说明的是, 在α 稳定分布噪声背景下, 理论上DCM并不存在^[12], 但是为了与SCM进行对比实验, 仍然进行了该方面的实验, 从实验结果可以看到, α 稳定分布噪声(α =1.8)背景下基于DCM的信源数目估计算法是具有一定的估计性能的, 这是因为在仿真中应用的是有限时长数据, 并不能达到理论上的无限大。

3.1 特征值分解方法

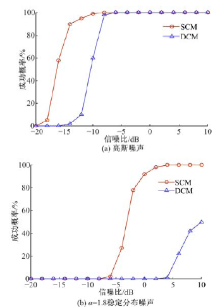
首先分析基于SCM与DCM的特征值分解方法的性能。从图2中可以看到, 在高斯噪声下, 基于DCM的特征值方法, 在信噪比高于-10 dB时才可能正确判断信源数目, 在信噪比高于-7 dB时, 才能接近信源数目估计100%的正确率。而基于SCM的特征值方法, 在信噪比高于-15 dB时即可正确估计信源数目, 而当信噪比高于-10 dB时, 估计准确率基本达到100%。而在α 稳定分布噪声下, 基于DCM的特征值法在信噪比高至10 dB时, 也只能达到50%左右的正确率, 而基于SCM的方法在5 dB时已经基本达到100%的正确率, 且在信噪比低至0 dB时, 仍有80%的成功率, 说明在应用特征值分解法的情况下, 利用SCM比利用DCM具有更好的估计性能。

	Figure Option View Download New Window
	图2 基于DCM和SCM的特征值分解法比较Fig.2 Comparison of eigenvalue decomposition method based on DCM and SCM

3.2 盖氏圆方法

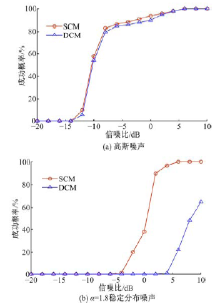
图3给出了基于SCM和DCM盖氏圆法的信源数目估计结果。从图3中可以看到, 在高斯噪声条件下, 基于SCM和基于DCM的盖氏圆方法的估计成功率基本相当, 在信噪比低至-10 dB时仍有一定的检测概率, 当信噪比达到5 dB以上时, 基本可以达到100%的准确率。而在α 稳定分布噪声下, 基于DCM的盖氏圆法在信噪比为10 dB时, 才能达到70%左右的成功率, 而基于SCM的盖氏圆方法在信噪比为5 dB时已达100%的成功率, 且在2 dB时可以达到90%的成功率。实验结果与3.1小节相类似, 即基于SCM的盖氏圆方法具有比基于DCM的盖氏圆方法更好的估计性能。

	Figure Option View Download New Window
	图3 基于DCM和SCM的盖氏圆法比较Fig.3 Comparison of Gerschgorin radii based on DCM and SCM

3.3 Otsu类间方差法

前面所述的特征值法、盖氏圆法等信号源数目估计方法, 都是基于特征值分类的, 其基本思想都是基于协方差矩阵的特征值可以分为信号特征值(大特征值)与噪声特征值(小特征值)两类这一事实的。所以信源数目估计问题本质上是一个样本的分类问题, 而在分类问题中, 模式识别中的很多方法是行之有效的, 由于本问题的特征明确, 分类数少(只有两类), 所以选取模式识别领域中的一种简单且优秀的分类识别方法— — Otsu类间方差法^[10]用于本节所研究的信源数目估计问题中。

使用Otsu类间方差法进行样本分类的基本目标是使分类结果的类间方差达到最大, 类间方差表示的是所分的两类样本重心与总样本重心之间的平均距离。假设样本的升序排列(或降序排列)为Λ =[λ ₁, λ ₂, …, λ _N], 以某一个样本值λ _P为阈值将样本分为两类, Λ ₁=[λ ₁, λ ₂, …, λ _P]和Λ ₂=[λ _P+₁, λ _P+₂, …, λ _N]。则两类的重心分别为:

$μ_{1} = \frac{1}{P} \overset{P}{\sum_{i = 1}} λ_{i} (21)$

$\begin{matrix} \begin{matrix} μ_{2} = \frac{1}{N - P} \overset{N}{\sum_{i = P + 1}} λ_{i} (22) \end{matrix} \end{matrix}$

样本集的重心定义为:

$\begin{matrix} μ = \frac{1}{N} \overset{N}{\sum_{i = 1}} λ_{i} (23) \end{matrix}$

则类间方差定义为:

$\begin{matrix} C (P) = P (μ_{1} {- μ)}^{2} + (N - P) (μ_{2} {- μ)}^{2} (24) \end{matrix}$

求取使得类间方差达到最大值的P值, 即可得到基于最大类间方差准则的分类结果, 分类结果中, 代表大特征值的一组的个数, 即为信源数目的估计值。如果样本为降序排列, 估计值为P, 反之以升序排列, 则估计值为N-P。

仿真实验:实验条件如同前面所述, 即噪声取高斯和α 稳定分布噪声两种, 每种噪声的信噪比从-20 dB到10 dB, 每个信噪比点做1000次蒙特卡罗实验, 记录正确估计信源数目的成功概率。

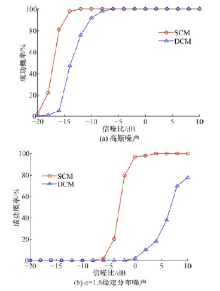
	Figure Option View Download New Window
	图4 基于DCM和SCM的Otsu类间方差法比较Fig.4 Comparison of Otsu class variance method based on DCM and SCM

图4给出高斯噪声下和α 稳定分布噪声下基于Otsu方法的信源数目估计成功概率曲线。

由图4中可以看到, 高斯噪声下, 基于SCM的Otsu类间方差法明显优于基于DCM的, 且在-15 dB时即可达到80%的成功率, 而基于DCM的Otsu类间方差法在-10 dB时才基本达到80%的成功率。在α 稳定分布噪声下, 基于SCM的Otsu方法在0 dB时即可达到接近100%的成功率, 而基于DCM的Otsu方法在信噪比高至10 dB时才能达到80%左右的成功概率。说明针对Otsu类间方差法, 利用SCM比DCM仍然可以达到更好的估计效果。另外, 在同样利用SCM或DCM时, 把本实验中Otsu类间方差法与前两个实验中的特征值法和盖氏圆法进行比较, 可以发现, 相同条件下, Otsu类间方差法具有比另外两种方法更高的估计成功率。

4 结束语

针对阵列信号处理中信源数目估计的问题, 提出了一种利用SCM的Otsu最大类间方差方法估计信源数目的方法。首先, 针对独立同分布噪声在非零延迟出相关函数为零的特性, 定义了一种移位协方差矩阵, 理论分析表明SCM的大特征值与小特征值的区别要比DCM的更加显著。然后, 在此基础上提出了一种利用Otsu最大类间方差的信源数目估计方法。仿真实验表明:相同条件下, 基于SCM的信源数目估计方法性能要明显优于基于DCM的; 而且基于SCM的Otsu最大类间方差的信源数目估计方法要比同样基于SCM的特征值方法和盖氏圆方法具有更好的估计性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Dmochowski J, Benesty J, Affes S. Direction of arrival estimation using the parameterized spatial correlation matrix[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(4): 1327-1339. [本文引用:1]
[2]	Wan F, Zhu W, Swamy M N S. Spacial extrapolation-based blind DOA estimation approach for closely spaced sources[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 569-582. [本文引用:1]
[3]	Reddy V V, Ng B P, Khong A W H. Derivative-constrained frequency-domain wideband DOA estimation[J]. Multidimensional Systems and Signal Processing, 2014, 25(1): 211-233. [本文引用:1]
[4]	Yan F G, Jin M, Liu S, et al. Real-valued MUSIC for efficient direction estimation with arbitrary array geometries[J]. IEEE Transactions on Signal Processing, 2014, 62(6): 1548-1560. [本文引用:1]
[5]	Sharma K, Santosh S. A review on ESPRIT—estimation of signal parameters via rotational invariance techniques[J]. International Journal of Engineering Research, 2013, 2(3): 243-252. [本文引用:1]
[6]	单泽彪, 石要武, 刘小松, 等. 应用人工蜂群算法的动态波达方向跟踪[J]. 光学精密工程, 2015, 23(3): 838-845. Shan Ze-biao, Shi Yao-wu, Liu Xiao-song, et al. DOA tracking of moving targets by artificial bee colony algorithm[J]. Optics and Precision Engineering, 2015, 23(3): 838-845. [本文引用:1]
[7]	单泽彪, 石要武, 刘小松, 等. 时变遗忘因子动态DOA跟踪算法[J]. 吉林大学学报: 工学版, 2016, 46(2): 632-638. Shan Ze-biao, Shi Yao-wu, Liu Xiao-song, et al. DOA tracking algorithm of moving targets with variable forgetting factor[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(2): 632-638. [本文引用:1]
[8]	石要武, 陈淼, 单泽涛, 等. 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计[J]. 吉林大学学报: 工学版, 2017, 47(1): 268-273. Shi Yao-wu, Chen Miao, Shan Ze-tao, et al. Spatial smoothing technique for coherent signals DOA estimation via eigen space MUSIC algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(1): 268-273. [本文引用:2]
[9]	张小飞, 陈华伟, 仇小锋, 等. 阵列信号处理及MATLAB实现[M]. 北京: 电子工业出版社, 2015. [本文引用:5]
[10]	张新明, 孙印杰, 郑延斌. 二维直方图准分的Otsu 图像分割及其快速实现[J]. 电子学报, 2011, 39(8), 1778-1784. Zhang Xin-ming, Sun Yin-jie, Zheng Yan-bin. Precise two-dimensional Otsu's image segmentation and its fast recursive realization[J]. Acta Electronica Sinica, 2011, 39(8): 1778-1784. [本文引用:2]
[11]	Nikias C L, Shao M. Signal Processing with Alpha Stable Distribution and Applications[M]. New York: John Wiley & Sons Inc, 1995. [本文引用:1]
[12]	Swami A, Sadler B M. On some detection and estimation problems in heavy-tailed noise[J]. Signal Processing, 2002, 82(10): 1471-1488. [本文引用:1]

2007

0.0

... 0 引言阵列信号处理是将一组传感器按一定方式布置在空间的不同位置上,形成传感器阵列,用传感器阵列来接收空间信号,其在通信、雷达、声纳和地震勘探等领域有着广泛的应用^[1,2,3] ...

2010

0.0

2014

0.0

2014

0.0

... 子空间类的MUSIC^[4]和ESPRIT^[5]系列算法因具有超分辨能力而得到了广泛的关注和研究 ...

2013

0.0

... 子空间类的MUSIC^[4]和ESPRIT^[5]系列算法因具有超分辨能力而得到了广泛的关注和研究 ...

2015

0.0

. 2015, 23(3):838-845

DOA tracking of moving targets by artificial bee colony algorithm

应用人工蜂群算法的动态波达方向跟踪

Shan Ze-biao , Shi Yao-wu , Liu Xiao-song

单泽彪, 石要武, 刘小松

... 这一类算法中,一般要求空间信号源数目已知^[6,7,8],进而为信号子空间和噪声子空间的分离提供支持,所以对空间信号源数目的准确估计是这一类算法进行波达方向等参数估计的前提 ...

2016

0.0

. 2016, 46(2):632-638 DOI:doi:10.13229/j.cnki.jdxbgxb201602044

DOA tracking algorithm of moving targets with variable forgetting factor

时变遗忘因子动态DOA跟踪算法

Shan Ze-biao , Shi Yao-wu , Liu Xiao-song

单泽彪, 石要武, 刘小松

摘　要：针对目标信号源波达方向（DOA）实时变化的情况,提出了一种时变遗忘因子的自适应样本协方差矩阵更新方法。时变遗忘因子根据DOA变化的快慢自适应调节自身的大小,从而合理地调整历史数据及当前采样数据在协方差矩阵更新过程中所占的权重。在更新协方差矩阵后,对其直接应用最大似然估计方法,并将序列二次规划（SQP）应用于似然函数的优化求解上,最终实现了DOA的动态跟踪。仿真结果表明：该算法具有解相干的能力和良好的跟踪精度,并且在小样本、低信噪比下仍能达到比较满意的跟踪效果。

2017

0.0

. 2017, 47(1):268-273 DOI:doi:10.13229/j.cnki.jdxbgxb201701039

Spatial smoothing technique for coherent signals DOA estimation via eigen space MUSIC algorithm

基于特征空间MUSIC算法的相干信号波达方向空间平滑估计

Shi Yao-wu , Chen Miao , Shan Ze-tao

石要武, 陈淼, 单泽涛

摘　要：为了高效、准确地估计相干信号的波达方向（DOA）,提出了一种基于特征空间多重信号分类（MUSIC）算法的空间平滑估计方法。首先对相干信号进行空间平滑处理,然后对其应用特征空间MUSIC算法进行DOA的精确估计,使其最大限度地利用信号子空间和噪声子空间的信息。本文方法并不影响非相关信号存在时DOA的估计,且还可以对信号源功率进行有效的估计,以提高对小能量信号的成功估计概率。与传统空间平滑算法及修正MUSIC算法相比,本文方法具有更低的信噪比门限和更高的估计精度及分辨力。最后的仿真实验验证了本文方法的有效性和鲁棒性。

... 可以证明得到特征值服从以下排序^[8]:#cod#x003bb ...

2015

0.0

... 现有的信源数目估计方法包括特征值分解方法、信息论方法、盖氏圆方法和正则相关方法等^[9],这些方法均是针对高斯噪声下的信源数目估计问题而提出的,都是基于#cod#x0201c ...

... 由于较小的特征值对应噪声功率,当噪声功率较小时,大特征值与小特征值之间可以明确区分,进而可以根据较大特征值的数量得到信源数目的估计,这便是特征值分解法估计信源数目的基础^[9] ...

... 同时根据窄带信号的定义可知频率与带宽B的关系为^[9]: ...

... 下面分别以特征值分解方法^[9]、盖氏圆法^[9]和Otsu类间方差法为例,采用蒙特卡罗仿真实验的方法,分别对DCM和SCM执行这3种算法,以比较其性能 ...

2011

0.0

. 2011, 39(8):1778-1784

Precise two-dimensional Otsu's image segmentation and its fast recursive realization

二维直方图准分的Otsu 图像分割及其快速实现

Zhang Xin-ming , Sun Yin-jie , Zheng Yan-bin.

张新明, 孙印杰, 郑延斌

传统二维Otsu法主要由于对二维直方图采用主对角线区域概率和近似为1的假设等原因,以致分割结果不够准确.针对此问题,提出了一种二维直方图准分的Otsu快速图像分割方法.(1)准确选择邻域模板构建二维直方图并将Otsu阈值法用于此直方图上以便提高分割性能;(2)对二维直方图主对角线上的目标和背景两区域的Otsu公式中对应量准确取值使阈值选取更准确;(3)对二维直方图投影进行分析得到其特性,并证明三个定理的存在,利用此特性和三个定理导出新型、快速的递推算法来降低计算复杂度.实验结果表明:与当前二维Otsu阈值法相比,本文提出的方法分割更准确和抗噪性更强,而且其运行时间少,与当前二维Otsu斜分递推算法的运行时间相近.

... 本文提出移位协方差矩阵的概念及其特征值分布的特征,进而提出用Otsu类间方差法^[10]进行信源数目估计的方法 ...

... Otsu类间方差法^[10]用于本节所研究的信源数目估计问题中 ...

1995

0.0

... 稳定分布^[11]噪声下,本文方法同样具有良好的性能 ...

2002

0.0

... 稳定分布噪声背景下,理论上DCM并不存在^[12],但是为了与SCM进行对比实验,仍然进行了该方面的实验,从实验结果可以看到,#cod#x003b1 ...