基于稀疏矩阵的谱聚类图像分割算法

引用本文

刘仲民, 李战明, 李博皓, 胡文瑾. 基于稀疏矩阵的谱聚类图像分割算法. 2017, 47(4): 1308-1313
LIU Zhong-min, LI Zhan-ming, LI Bo-hao, HU Wen-jin. Spectral clustering image segmentation based on sparse matrix. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1308-1313 复制到剪切板

Permissions

基于稀疏矩阵的谱聚类图像分割算法

刘仲民¹, 李战明¹, 李博皓¹, 胡文瑾²

1.兰州理工大学电气工程与信息工程学院,兰州 730050

2.西北民族大学数学与计算机学院,兰州 730030

通讯作者：李战明(1962-),男,教授,博士生导师.研究方向:复杂系统的建模与控制,智能信息处理与模式识别.E-mail:liuzm@lut.edu.cn

作者简介:刘仲民(1978-),男,副教授,博士研究生.研究方向:机器视觉,智能信息处理与模式识别.E-mail:liuzhmx@163.com

基金:国家自然科学基金项目(61561042); 西北民族大学引进人才基金项目(1310RJYA013).

摘要

在图像分割中谱聚类算法需要计算像素之间的相似度矩阵,构造数据量大,并且要对拉普拉斯矩阵进行特征分解,计算比较耗时。针对这一问题,提出了一种基于稀疏矩阵的谱聚类图像分割算法。算法结合图像特征信息在不同尺度上对谱聚类进行误差分析,设计了一种新的样本信息选取方案,并利用选取的图像信息直接创建稀疏相似度矩阵。理论分析以及图像分割实验结果表明,该算法能够有效降低谱聚类的计算复杂度,同时,提高了分割的准确性和鲁棒性。

关键词: 信息处理技术; 计算机应用; 图像分割; 谱聚类; 稀疏矩阵; K均值

中图分类号:TP911.1 文献标志码:A 文章编号:1671-5497(2017)04-1308-06

Spectral clustering image segmentation based on sparse matrix

LIU Zhong-min¹, LI Zhan-ming¹, LI Bo-hao¹, HU Wen-jin²

1.College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China

2.College of Mathematic and Information Technology,Northwest University for Nationalities, Lanzhou 730030, China

Abstract

Spectral clustering based on the similarity while the structure of similarity matrix is complex in image segmentation. The calculation of spectral clustering can be very time-consuming, especially in the process of Eigen-decomposition for Laplacian matrix. Sparse matrix could obtain the approximate solution of the similarity matrix by sing a small amount of sample information, thus, reducing the computational complexity effectively. An image segmentation algorithm based on the sparse matrix is proposed. First, error analysis of the spectral clustering is carried out in different scales. Then, a novel sampling method is presented. The sample information is used to create a sparse matrix, which can be used to substitute the similarity matrix. Typical experiment results and theoretical analysis show that the proposed algorithm can effectively reduce the complexity in calculating spectral clustering and improve the accuracy and robustness of the segmentation.

Keyword: information processing technology; computer application; image segmentation; spectral clustering; sparse matrix; K-means

Show Figures

0 引言

谱聚类是一种新型的聚类分析方法, 具有能够处理任意形状的数据集、易于执行等优点^[1]。近年来谱聚类算法开始应用于图像分割及其相关领域并取得了迅速发展^{[2, 3]}。该方法通过计算像素之间的相似度矩阵和拉普拉斯矩阵并对拉普拉斯矩阵进行特征分解, 通过对特征向量进行聚类完成对图像的划分。该算法基于相似度矩阵将图像划分为多个区域, 使得同一区域内部像素点相似度高, 不同区域之间相似度低, 从而可以获得较理想的分割效果。然而, 该算法在计算过程中产生的相似度矩阵规模过大, 特征值与特征向量的计算、存储使得算法计算复杂度过高。

过高的计算复杂度严重制约了谱聚类在图像分割领域中的应用。针对这一问题, 国内外学者进行了一系列的研究和改进, 其中有学者提出利用“ 稀疏矩阵” 的方法对其进行改进。稀疏矩阵指的是非零元素占全部元素的百分比很小或者非零元素占全部元素的百分比较大但是分布很有规律的矩阵。利用稀疏矩阵的结构特点可以避免储存零元素或避免对零元素进行运算从而减少内存消耗提高运算效率。代表方法有t-nearest-neighbor方法^[4], e-neighborhood方法^[5]和“ random” 方法^[6]等。其中t-nearest-neighbor方法只保留相似度矩阵中与样本点取值相关的t邻域之内的数, 其余数据都忽略为零。e-neighborhood方法设定阈值e并将相似度矩阵中小于e的值都近似为零。这两种方法虽然能够减小拉普拉斯矩阵特征分解的计算复杂度, 但仍然需要预先算出相似度矩阵中的所有元素, 计算量依旧很大。random方法是随机指定相似度矩阵中一些元素为0, 从而计算量大大减小, 但该方法没有考虑样本之间的关系, 实验结果明显劣于前两种。

针对以上问题, 本文提出了一种新的基于稀疏矩阵的谱聚类图像分割算法。该算法在不同尺度范围内对像素相似度进行误差分析, 通过最小化误差的准则分别提取边缘和区域特征信息, 利用所提取的特征信息创建稀疏矩阵并代替原相似度矩阵进行运算。经理论分析与实验仿真证明, 本文算法不仅能有效降低谱聚类的计算复杂度, 而且能够获得更加令人满意的分割结果。

1 谱聚类及其应用

1.1 谱聚类算法

谱聚类是一种基于图论的聚类算法^[7]。图由若干点及连接两点的线构成, 用点代表事物, 线表示对应两个事物间具有的某种关系, 又称为权重。将图划分为若干个子图, 各子图无交集, 划分时子图之间被“ 截断” 的线的权重和称为损失函数。谱聚类通过最小化损失函数来实现图的划分。设G(V, E)表示图, V={v₁, v₂, …, v_n}表示点集, E表示边集。w_ij 表示v_i 与v_j 之间权重。假设G(V, E)被划分成G₁ 、G₂ 两个子图, 定义q=[q₁, q₂, …, q_n]是一个n维向量, 用来表示划分方案。

$\begin{matrix} q_{i} = \{\begin{matrix} c_{1}, i \in G_{1} \\ c_{2}, i \in G_{2} \end{matrix} (1) \end{matrix}$

损失函数可定义为:

$\begin{matrix} \begin{matrix} Cut (G_{1}, G_{2}) = \sum_{i \in G_{1}, j \in G_{2}} w_{ij} = \\ \frac{\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} w_{ij} (q_{i} - q_{j})^{2}}{2 (c_{1} - c_{2})^{2}} (2) \end{matrix} \end{matrix}$

$\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} w_{ij} (q_{i} - q_{j})^{2} = 2 q^{T} (D - W) q (3)$

式中: $\begin{matrix} W 为权重矩阵; D \end{matrix}$ 为对角矩阵。

$\begin{matrix} D_{ii} = \overset{n}{\sum_{j = 1}} w_{ij} (4) \end{matrix}$

定义拉普拉斯矩阵L=D-W, 将最小化损失函数的问题转化为最小化q^T Lq的问题。

1.2 谱聚类在图像分割中的应用

谱聚类图像分割算法将图像中的像素看作图中的点V, 像素之间的相似度关系可看作图中连接各顶点的线E, 构造出基于像素相似度的加权无向图G(V, E), 并以此进行分割, 其具体步骤如下:

Step1将待分割图像映射为加权无向图G(V, E)。

Step2计算相似度矩阵W以及拉普拉斯矩阵L。

Step3对拉普拉斯矩阵 $\begin{matrix} L \end{matrix}$ 进行特征分解, 求出特征值与特征向量。

Step4对特征向量进行聚类, 完成图像分割。

利用高斯函数计算图像各像素点之间相似度^[8], 如式(5)所示:

$\begin{matrix} ω_{ij} = e^{\frac{- ‖ F (i) - F (j) ‖_{2}^{2}}{σ_{I}}} \times e^{\frac{- ‖ X (i) - X (j) ‖_{2}^{2}}{σ_{X}}} (5) \end{matrix}$

式中:F(• )表示灰度值; X(• )表示坐标; σ _I 、σ _X分别表示灰度差值与坐标距离的尺度参数。

2 图像特征信息提取

图像分割离不开对图像底层视觉信息的利用, 包括边缘与区域特性。相似度矩阵是决定谱聚类图像分割质量的最重要因素。在创建相似度矩阵时只有有效利用了边缘和区域的特征信息才能获得理想的分割效果。对相似度函数(5)进行分析可知, 随着坐标距离的变大, $\begin{matrix} σ_{X} \end{matrix}$ 值越小函数值的衰减速度则越快。但较小的 $\begin{matrix} σ_{X} \end{matrix}$ 值会导致函数值迅速衰减趋近于零, 无法正确反映不同区域之间像素的相似度。 $\begin{matrix} σ_{X} \end{matrix}$ 值较大时函数值衰减速度慢, 但较低的距离敏感性会使得所建相似度矩阵对图像边缘信息的利用不够充分。为了创建更为精确的稀疏相似度矩阵, 本文将在不同的距离尺度参数下, 分别提取边缘与区域特征信息。

2.1 边缘特征信息提取

由于在较小的距离尺度参数 $\begin{matrix} σ_{X} \end{matrix}$ 下, 像素的相似度取值在一定邻域内变化剧烈, 而相似度矩阵包含较多的边缘信息。为此假设该邻域范围为 $\begin{matrix} r, \end{matrix}$ 定义新的像素点相似度公式如下:

$\begin{matrix} \begin{matrix} ω_{ij} = e^{\frac{- ‖ F (i) - F (j) ‖_{2}^{2}}{σ_{I}}} \times \\ \{\begin{matrix} e^{\frac{- ‖ X (i) - X (j) ‖_{2}^{2}}{σ_{X}}}, ‖ X (i) - X (j) ‖_{2} < r \\ 0, ot h erwise \end{matrix} (6) \end{matrix} \end{matrix}$

在邻域r范围内式(5)(6)可以得到相等的ω _ij 值, 在r范围外式(5)中相似度取值趋近于0, 与式(6)的取值近似相等。因此用式(6)代替式(5)创建的稀疏矩阵将与原相似度矩阵有较小误差, 不仅减小了计算量, 而且可以获得理想的边缘信息。

2.2 区域特征信息提取

在较大的距离尺度参数 $\begin{matrix} σ_{X} \end{matrix}$ 下, 相似度取值随距离变化平缓, 不同区域的像素之间相似度的计算结果更为精确。本文将寻找图像各区域的特征中心, 通过计算所有像素与特征中心的相似度, 完成对区域信息的提取^[9]。

2.2.1 区域最小误差分析

对图像进行特征提取并创建稀疏矩阵, 要保证创建的稀疏矩阵S与原相似度矩阵W之间的误差最小化。对于一幅确定的图像, 相似度矩阵的‖ W‖ _F 为一大于0的常数。稀疏矩阵S由W中提取的少量元素与零组成, 因此‖ S‖ _F≤ ‖ W‖ _F 。最小化误差就要保证最大化稀疏矩阵的‖ S‖ _F 。设X={x₁…x_j…x_n}为所有像素的集合, Z={z₁…z_i…v_m}为所有特征中心的集合。

$\begin{matrix} ‖ S ‖_{F}^{2} = \overset{n}{\sum_{j = 1}} \overset{m}{\sum_{i = 1}} k {(z_{i}, x_{j})}^{2} (7) \end{matrix}$

式中:k(z_i, x_j)表示像素x_j 与特征中心z_i 之间的相似度, 本文所取相似度矩阵函数k(z_i, x_j)为高斯核函数, k(z_i, x_j)取值与x_j 、z_i 之间的距离d(z_i, x_j)负相关。即最大化‖ S‖ _F 等价于最小化D。

$\begin{matrix} D = \overset{n}{\sum_{j = 1}} \overset{m}{\sum_{i = 1}} d {(z_{i}, x_{j})}^{2} (8) \end{matrix}$

从而可以通过 $\begin{matrix} K \end{matrix}$ 均值聚类算法获得特征中心^[10]。

2.2.2 区域特征信息提取方法

通过区域误差分析, 可以利用K均值聚类算法寻找区域特征中心。然而灰度图像拥有个特征值, 分别为x坐标、y坐标灰度值I(x, y)。由于无法准确预估坐标与灰度值之间的权重关系, 因此无法直接利用K均值进行计算。K均值聚类满足迭代误差ε 最小化, 本文利用该特性寻找区域特征中心。具体步骤如下:

输入:给定图像I, 像素个数n, 特征中心个数m, 终止迭代参数σ 。

输出:特征中心 $\begin{matrix} Q 。 \end{matrix}$

Step1 按照设定的特征中心个数m, 在图像I上进行均匀采样, 并将像素分配到与之最近的采样点。

Step2 计算采样点3× 3邻域内像素点的灰度梯度值, 选取梯度值最小的点作为新的采样点。

Step3 设置步长s=(n∕ m)^1⁄2, 在2s× 2s邻域内按照距离(式(9))为每一个采样点分配像素。

$\begin{matrix} d = d_{x, y} + d_{I (x, y)} (9) \end{matrix}$

式中:d_{x, y}为坐标的欧氏距离, d_{I(x, y)}为灰度差的绝对值。

Step4 求取采样点所属像素的平均值作为新的采样点 $\begin{matrix} Q, \end{matrix}$ 计算新旧采样点误差:

$\begin{matrix} ε = ε_{x, y} + ε_{I (x, y)} (10) \end{matrix}$

式中:ε _{x, y}为坐标误差; ε _{I(x, y)}为灰度值误差。如果ε < σ 转Step5; 否则转Step3。

Step5 输出 $\begin{matrix} Q \end{matrix}$ 作为区域特征中心。

该算法在分配数据时充分利用像素点与采样中心之间的距离关系, 使得误差最小化。根据 $\begin{matrix} K \end{matrix}$ 均值聚类算法可得知, 通过Step1在空间上进行均匀采样可得到最小化的 $\begin{matrix} ε_{x, y} 。 \end{matrix}$ 利用Step2可以防止采样点落在噪音或者边界上。在此基础上, Step3和Step4计算每个采样中心拥有像素的灰度值, 并在一定范围内变化像素点所属采样中心, 并更新采样中心坐标, 利用迭代的方式最小化灰度值误差ε _{I(x, y)。}

3 创建稀疏矩阵及图像分割算法

3.1 稀疏矩阵的创建

稀疏矩阵的创建过程是稀疏矩阵谱聚类图像分割的重要步骤。为了避免对图像中所有像素进行计算, 本文对图像中所有像素进行编码, 并将提取的特征信息映射到相似度矩阵中。

创建稀疏矩阵的具体过程分为两部分。第一部分提取创建稀疏矩阵所需特征信息(Step1~Step5); 第二部分将特征信息映射到稀疏矩阵(Step6~Step10)。以边缘信息特征提取为例, 对于一幅 $\begin{matrix} m \times n \end{matrix}$ 的图像, 稀疏矩阵创建步骤如下:

Step1 计算每个像素与邻域像素的灰度差值, 得到灰度差值矩阵Q₁, Q₂, …, Q_N, 根据灰度差值矩阵计算灰度相似度矩阵W₁, W₂, …, W_N:

$\begin{matrix} \begin{matrix} W_{ij} = e^{\frac{- ‖ Q_{ij} ‖_{2}^{2}}{σ_{I}}} (11) \\ i = 1, 2, \dots, m; j = 1, 2, \dots, n \end{matrix} \end{matrix}$

Step2 将每个灰度相似度矩阵转化为一维列矩阵 $\begin{matrix} E_{1}, E_{2}, \dots, E_{N} : \end{matrix}$

$\begin{matrix} \begin{matrix} E_{i + (j - 1) \times m} = W_{ij} (12) \\ i = 1, 2, \dots, m; j = 1, 2, \dots, n \end{matrix} \end{matrix}$

合并得到灰度特征信息矩阵 $\begin{matrix} E = [E_{1}, E_{2}, \dots, E_{N}] 。 \end{matrix}$

Step3 计算每个像素与邻域像素坐标的欧氏距离, 得到坐标差值矩阵R₁, R₂, …, R_N, 根据坐标差值矩阵计算坐标相似度矩阵T₁, T₂, …, T_N:

$\begin{matrix} \begin{matrix} T_{ij} = e^{\frac{- ‖ R_{ij} ‖_{2}^{2}}{σ_{I}}} (13) \\ i = 1, 2, \dots, m; j = 1, 2, \dots, n \end{matrix} \end{matrix}$

Step4 将每个坐标相似度矩阵转化为一维列矩阵 $\begin{matrix} Y_{1}, Y_{2}, \dots, Y_{N} : \end{matrix}$

$\begin{matrix} \begin{matrix} Y_{i + (j - 1) \times m} = T_{ij} (14) \\ i = 1, 2, \dots, m; j = 1, 2, \dots, n \end{matrix} \end{matrix}$

合并得到距离特征信息矩阵Y=[Y₁, Y₂, …, Y_N]

Step5 距离特征信息矩阵与灰度特征信息矩阵对应位置相乘得到边缘特征信息矩阵 $\begin{matrix} U : \end{matrix}$

$\begin{matrix} \begin{matrix} U_{ij} = T_{ij} \times E_{ij} (15) \\ i = 1, 2, \dots, m \times n; j = 1, 2, \dots, N \end{matrix} \end{matrix}$

Step6 按照坐标对像素编码, 得到像素编码矩阵 $\begin{matrix} A : \end{matrix}$

$\begin{matrix} \begin{matrix} A_{ij} = i + (j - 1) \times m (16) \\ i = 1, 2, \dots, m; j = 1, 2, \dots, n \end{matrix} \end{matrix}$

计算邻域像素编码矩阵 $\begin{matrix} A_{1}, A_{2}, \dots, A_{N} 。 \end{matrix}$

Step7 邻域像素编码矩阵化为一维列矩阵 $\begin{matrix} S_{1}, S_{2}, \dots, S_{N} \end{matrix}$

$\begin{matrix} \begin{matrix} S_{i + (j - 1) \times m} = A_{ij} (17) \\ i = 1, 2, \dots, m; j = 1, 2, \dots, n \end{matrix} \end{matrix}$

合并形成稀疏横坐标矩阵 $\begin{matrix} S = [S_{1}, S_{2}, \dots, S_{N}] 。 \end{matrix}$

Step8 生成一维列向量 $\begin{matrix} B \end{matrix}$

$\begin{matrix} B_{i} = i, i = 1, 2, \dots, m \times n (18) \end{matrix}$

复制 $\begin{matrix} N \end{matrix}$ 次并组合生成稀疏纵坐标矩阵 $\begin{matrix} D 。 \end{matrix}$

其中:

$\begin{matrix} D = \underset{N}{\underset{︷}{[B_{1}, B_{1}, B_{1}, \dots, B_{1}]}} (19) \end{matrix}$

Step9 $\begin{matrix} S 、 D 、 U \end{matrix}$ 化为一维, 得到3个向量。前2个向量中存储的是特征信息矩阵 $\begin{matrix} U \end{matrix}$ 中的值在稀疏矩阵中的坐标。直接按照向量赋值, 创建稀疏矩阵。

利用该方法创建稀疏矩阵可以避免对原相似度矩阵中所有元素进行计算, 计算复杂度由O(n²m²)降为O(Nnm), 需要运算及存储的数据量大大减少。例如邻域像素范围为5, 则N=25, 涉及相似度的计算量由m²n² 减少为25× mn。

3.2 本文算法

改进的谱聚类算法步骤如下:

Step1 按照本文算法分别提取边缘特征信息与区域特征信息, 并建立边缘稀疏矩阵S₁, 区域稀疏矩阵S₂, 最终得到相似度稀疏矩阵W=S₁+S₂ 。

Step2 计算拉普拉斯矩阵并进行特征分解, 将特征值由大到小排序后, 选择前 $\begin{matrix} k \end{matrix}$ 最小的特征值所对应的特征向量, 用矩阵 $\begin{matrix} V \end{matrix}$ 表示。

Step3 将矩阵 $\begin{matrix} V \end{matrix}$ 进行归一化, 并记归一化的矩阵为 $\begin{matrix} Y : \end{matrix}$

$\begin{matrix} Y_{ij} = \frac{V_{ij}}{\sqrt[]{\sum_{j} V_{ij}}} (20) \end{matrix}$

Step4 矩阵 $\begin{matrix} Y \end{matrix}$ 的每行视为样本, 用 $\begin{matrix} K \end{matrix}$ 均值聚类算法将它们聚为 $\begin{matrix} k \end{matrix}$ 类。

Step5 确定原像素点类别, 完成图像分割。

4 实验验证

本文实验环境为Windows10操作系统、Intel i3处理器、4 GB内存, 实验平台为MatlabR2012a。实验图像均来自Berkeley大学的BSD300图像数据库中的训练集和测试集, 在其中选取了大量不同类型的图像进行分割, 并选取标准手工分割、FCM、Nyströ m、Ncut等分割结果与本文算法进行对比。

4.1 视觉效果及量化指标对比

本文选取幅图像进行分割实验, 其视觉分割效果如图1所示。

	Figure Option View Download New Window
	图1 图像分割实验结果Fig.1 Experimental results of image segmentation

从4幅图像分割的视觉效果来看, 本文算法有着明显的优势。为验证上述结论的可靠性, 本文将经典的性能评价指标查全率Recall和查准率Precision^[11]引入到图像分割效果的性能评价过程中。

$\begin{matrix} \begin{matrix} Recall = TP / (TP + FN) (21) \\ Precision = TP / (TP + FP) (22) \end{matrix} \end{matrix}$

式中: TP表示检索出的相关信息量; FN表示未检索出的相关信息量; FP表示检索出的无关信息量。查准率说明算法排除干扰, 减少噪声的能力, 查全率说明算法避免遗漏的能力。查准率、查全率越大说明分割效果越好, 但是一般情况下查全率高, 查准率就低, 查全率低, 查准率高。在两者都要求高的情况下, 可以用F-score来衡量。

$\begin{matrix} F - score = \frac{2 \times Recall \times Precision}{Recall + Precision} (23) \end{matrix}$

本文图像分割结果的3项分割指标如表1所示。

表1 分割评价指标 Table 1 Evaluation parameter

通过表1的计算结果以及图像分割视觉效果可以直观地看出, 本文算法要明显优于其余几种方法, 本文方法对测试库中的图像是准确可靠的。

4.2 鲁棒性分析

图像质量对图像分割效果具有重要的影响, 当图像存在一定程度的噪声或模糊干扰时, 将严重降低图像的分辨质量^[12], 从而影响到算法对最终分割结果的计算, 因此有必要对该算法在不同程度噪声下的鲁棒性进行分析和讨论。

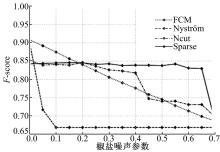
在对图1松树图像的分割当中4种算法都能获得较好的分割效果。为了对4种算法的鲁棒性进行验证, 在实验中对图像增加不同含量的椒盐噪声, 图像分割的F-score指标变化曲线如图2所示。

	Figure Option View Download New Window
	图2 F-score指标变化曲线Fig.2 F-score change curve

从图2可以看出, 在对图像施加噪声时其余3种算法的分割质量迅速变差, 而本文算法不仅有较好的分割结果, 稳定性也更强。

5 结束语

较高的计算复杂度严重限制了谱聚类算法在图像分割中的应用。为此, 提出了一种基于稀疏矩阵的谱聚类图像分割算法。该算法利用像素在不同尺度上的相似度关系, 通过最小化相似度矩阵与稀疏矩阵在边缘和区域上的误差提取特征信息创建稀疏相似度矩阵。经理论分析与实验仿真可证明:该算法不仅有效降低了谱聚类图像分割的计算量与计算复杂度, 节省了内存空间, 而且提高了图像分割质量, 提高了算法对噪声的抗干扰能力, 有更强的鲁棒性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	蔡晓妍, 戴冠中, 杨黎斌. 谱聚类算法综述[J]. 计算机科学, 2008, 35(7): 14-18. Cai Xiao-yan, Dai Guan-zhong, Yang Li-bin. Survey on spectral clustering algorithms[J]. Computer Science, 2008, 35(7): 14-18. [本文引用:1]
[2]	章毓晋. 图像分割中基于过渡区技术的统计调查[J]. 计算机辅助设计与图形学学报, 2015, 27(3): 379-381. Zhang Yu-jin. A survey on transition region-based techniques for image segmentation[J]. Journal of Computer-Aided Design and Computer Graphics, 2015, 27(3): 379-381. [本文引用:1]
[3]	Zhu Z, Wang L. Initialization approach for fuzzy C-means algorithm for color image segmentation[J]. Application Research of Computers, 2015, 32(4): 1257-1260. [本文引用:1]
[4]	Gou S, Zhuang X, Zhu H, et al. Parallel sparse spectral clustering for SAR image segmentation[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2013, 6(4): 1949-1963. [本文引用:1]
[5]	Jia H J, Ding S F. A spectral clustering algorithm based on neighborhood rough sets reduction[J]. Journal of Nanjing University, 2013, 49(5): 619-627. [本文引用:1]
[6]	Fulger D, Scalas E. Spectral properties of correlation matrices—towards enhanced spectral clustering[J]. Methods in Molecular Biology, 2011, 696: 381-411. [本文引用:1]
[7]	侯叶, 郭宝龙. 基于图论的运动对象分割[J]. 吉林大学学报: 工学版, 2008, 38(4): 902-906. Hou Ye, Guo Bao-long. Motion segmentation based on graph theory[J]. Journal of Jilin University(Engineering and Technology), 2008, 38(4): 902-906. [本文引用:1]
[8]	Shi J, Maiik J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 22(8): 888-905. [本文引用:1]
[9]	Bai X D, Cao Z G, Wang Y, et al. Image segmentation using modified SLIC and Nyström based spectral clustering[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(16): 4302-4307. [本文引用:]
[10]	Zhang K, Kwok J T. Clustered Nyström Method for large scale manifold learning and dimension reduction[J]. IEEE Transactions on Neural Networks, 2010, 21(10): 1576-1587. [本文引用:1]
[11]	Crevier D. Image segmentation algorithm development using ground truth image data sets[J]. Computer Vision & Image Understand ing, 2008, 112(2): 143-159. [本文引用:1]
[12]	宋艳涛, 纪则轩, 孙权森. 基于图像片马尔科夫随机场的脑MR图像分割算法[J]. 自动化学报, 2014(8): 1754-1763. Song Yan-Tao, Ji Ze-Xuan, Sun Quan-Sen. Brain MR image segmentation algorithm based on Markov rand om field with image patch[J]. Acta Automatica Sinica, 2014(8): 1754-1763. [本文引用:1]

2008

0.0

... 0 引言谱聚类是一种新型的聚类分析方法,具有能够处理任意形状的数据集、易于执行等优点^[1] ...

2015

0.0

. 2015, 27(3):379-381

A survey on transition region-based techniques for image segmentation

图像分割中基于过渡区技术的统计调查

Zhang Yu-jin.

章毓晋

... 近年来谱聚类算法开始应用于图像分割及其相关领域并取得了迅速发展^[2,3] ...

2015

0.0

... 近年来谱聚类算法开始应用于图像分割及其相关领域并取得了迅速发展^[2,3] ...

2013

0.0

... 代表方法有t-nearest-neighbor方法^[4],e-neighborhood方法^[5]和#cod#x0201c ...

2013

0.0

... 代表方法有t-nearest-neighbor方法^[4],e-neighborhood方法^[5]和#cod#x0201c ...

2011

0.0

... 方法^[6]等 ...

2008

0.0

. 2008, 38(4):902-906

Motion segmentation based on graph theory

基于图论的运动对象分割

Hou Ye , Guo Bao-long.

侯叶, 郭宝龙

将两种基于图论的算法图切割与随机游走应用于运动对象的分割.利用图切割,通过构造网络图、HSV空间消除阴影、建立混合模型背景及运动区域最小切割自动完成运动对象的分割;利用随机游走,通过选择种子点、建立权函数、求解Dirichlet问题及形态滤波等交互地完成运动对象的分割.通过实验对两种算法的应用进行了研究.结果表明:基于图切割算法可针对单目标快速、有效地进行分割,并获得干净、光滑的分割结果;基于随机游走算法可针对微弱物体边界或低对比度的图像分割,可在不要求实时性的情况下获取更为精确的分割结果,为后续的跟踪、自动分割等处理提供基础.

... 1 谱聚类算法谱聚类是一种基于图论的聚类算法^[7] ...

2002

0.0

... 利用高斯函数计算图像各像素点之间相似度^[8],如式(5)所示: ...

2014

2010

0.0

... 从而可以通过 K均值聚类算法获得特征中心^[10] ...

2008

0.0

... 为验证上述结论的可靠性,本文将经典的性能评价指标查全率Recall和查准率Precision^[11]引入到图像分割效果的性能评价过程中 ...

2014

0.0

... 2 鲁棒性分析图像质量对图像分割效果具有重要的影响,当图像存在一定程度的噪声或模糊干扰时,将严重降低图像的分辨质量^[12],从而影响到算法对最终分割结果的计算,因此有必要对该算法在不同程度噪声下的鲁棒性进行分析和讨论 ...