真三维显示技术主要包括集成成像技术(Integral imaging)、全息显示技术和体显示技术等^{[1, 2, 3, 4]}。全息显示技术对光源、胶片处理及成像环境等方面都有非常严格的要求, 目前多用于记录静止的物体; 体显示技术受限于它的显示空间和显示范围; 相比之下, 集成成像技术的采集和成像过程简单, 是点到点的3D空间信息, 能够重构出包含全真色彩以及连续视差的3D影像, 即可用于静态场景也可用于动态视频显示, 记录的立体图像信息以普通二维图像的形式存在, 可以利用现有的数字图像处理方法进行处理。这使得集成成像技术几乎满足了人们对理想立体显示的各项要求, 具有很强的可行性和广阔的提升空间。

理想的集成成像系统主要包括采集和显示两部分^[5], 在采集过程中, 将具有记录功能的记录媒体(如摄影胶片、电荷耦合元件(CCD)或互补金属氧化物半导体(CMOS)等)置于透镜阵列的焦平面处, 当拍摄物体发出的光线透过透镜阵列投射到记录媒体上时, 记录媒体上的对应位置便保存了拍摄物体的图像信息, 将记录媒体上得到的图像称为立体元图像阵列, 将每个透镜元覆盖范围内的图像称为立体元图像。在显示过程中, 将立体元图像阵列通过高分辨率的显示设备(如投影仪、液晶显示器(LCD)或等离子显示屏(PDP)等)投射在透镜阵列上, 根据光路可逆原理, 透镜阵列对接收到的光线进行光学解码并汇聚成空间中真实存在的立体景象。显示过程中使用的透镜阵列可以是与采集过程中相同的透镜阵列, 也可以是其经过等比缩放后的透镜阵列。

通过光学器件记录空间物体的三维信息存在制作成本高、通用性差、场景范围小等问题^[6]。因此本文提出一种采用计算机虚拟生成立体元图像阵列的方法, 并通过实验进行了验证。

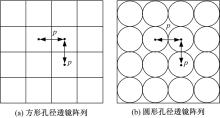
立体元图像阵列的生成方法主要包括透镜阵列采集法、计算机模拟采集法以及实景拍摄与计算机合成相结合的采集方法。如图1(a)所示, 透镜阵列采集法^{[7, 8]}是获得立体元图像阵列的最简单、直接的实景采集方法, 该方法使用透镜阵列和单一的图像记录媒体直接拍摄3D对象的立体元图像阵列, 但该方法存在很多不足, 较低的采集分辨率, 狭窄的观看视角以及较小的景深。计算机模拟采集法^{[9, 10]}利用高斯成像原理模拟真实相机的映射光路来获得立体元图像阵列。该方法无需实景采集设备, 因此避免了图像标定所带来的误差, 成本低、抗干扰能力强。图1(b)为实景拍摄与计算机合成结合的方法, 利用相机阵列模拟透镜阵列生成稀疏视点图像, 然后利用虚拟视点生成技术获得任意视点图像, 最后通过映射合成立体元图像阵列。该方法由于使用相机阵列模拟透镜阵列, 图像的标定与相机阵列的校准都会给系统带来误差, 而且成本高、采集效率低。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 立体元图像阵列生成方法Fig.1 Elemental images generation

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 本文方法整体框图Fig.2 Overall block diagram of proposed algorithm

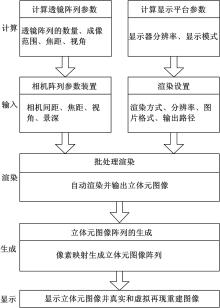
Maya是现在最为流行的顶级三维动画软件, 在国外绝大多数的视觉设计领域都在使用Maya。Maya有3种脚本语言, 用户可以根据自己的需求制作具有特定功能的Maya模型, 或者编写创建实现个性化功能的插件。如图2所示, 本文基于对立体元图像阵列生成方法的研究, 使用三维动画设计和制作软件Maya生成了可用于多种孔径透镜的立体元图像, 本文方法的整体框图见图2。

1.1 显示特性分析

首先要根据透镜阵列和显示平台的参数分析集成成像显示系统的性能, 从而设定相应参数。集成成像显示系统的性能主要由3个参数描述^[5]:立体图像的分辨率 R、视角 θ、立体图像的深度Δ Z。如图3所示, 立体图像的分辨率由显示器分辨率、透镜阵列到显示器间的距离以及透镜阵列的焦距决定, 它的大小为中心深度平面像点尺寸的倒数; 视角为可观看到无串扰和反转的立体图像的最大观测范围, 视角的大小与透镜元间距成正比, 与透镜阵列到显示器间的距离成反比; 立体图像的深度为中心深度平面两侧能够获得相同大小像点的成像范围, 距离中心深度平面越远, 像点越模糊。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 集成成像显示特性Fig.3 Viewing characteristics of integral imaging

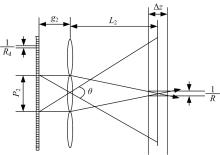
根据显示器到透镜间的距离 g2,可以将集成成像系统的显示模式分为分辨率优先 (g2> f)和深度优先 (g2=f)。两种显示模式下的分辨率 RI(分辨率优先)和 RD(深度优先)分别为:

RI=g2L2Rd1

RD=1P22

式中: Rd为显示器分辨率。当透镜元的间距 P2和透镜阵列的焦距 f确定后, 很容易可以得到组合成像系统的视角为:

θ=2arctan(P2/2g2)(3)

在考虑显示器分辨率对立体图像显示性能影响的基础上, 可以得到集成成像系统在分辨率优先和深度优先显示模式下的最大景深为:

ΔZI=minNf, d2λ4

ΔZ=2L2RIP25

式中:N为透镜元内所含像素的数量; L₂为中心深度平面与透镜阵列的距离。

由式(1)~(5)可以完成立体元图像阵列生成中各参数的设置。例如, 在深度优先的显示模式下想生成分辨率为60× 80、视角为12° 、深度为150 mm的立体图像, 则虚拟相机阵列的焦距为f=5 mm、虚拟相机间距P₂=1 mm, 虚拟相机视角12° , 渲染分辨率为30× 30。

1.2 批处理渲染

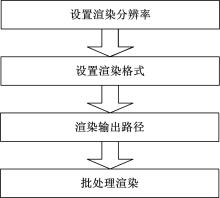
在Maya中, 通常是采用手动添加渲染相机的模式进行渲染的, 这对于庞大的相机阵列来说显然是不可能的。本文使用Maya脚本编写批处理渲染程序, 自动完成相机阵列的渲染并保存到相应路径下, 渲染进程如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 批处理渲染Fig.4 Batch render

1.3 立体元图像阵列的生成

Maya脚本渲染生成的立体元图像为单元图像, 因此要根据像素映射关系生成可用于集成成像显示的立体元图像阵列。具体方法如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 像素映射关系Fig.5 Pixel mapping relationship

相机阵列为 m×n、水平和垂直间距为 Δx, Δy)、渲染分辨率为 p×q,则第 (i, j)幅立体元图像(即单元图像)中的每个像素点与其对应的立体元图像阵列中像素的映射关系为:

E(x+p(i-1), y+q(j-1))=One(x, y)(6)

式中: One(x, y)为单元图像; E·为立体元图像阵列, 其分辨率为 mp×nq。

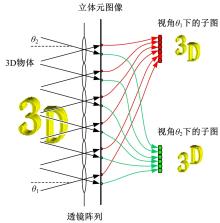
由组合成像系统中立体元图像阵列的生成过程可以看出, 每一幅立体元图像都从不同角度记录了三维物体的空间信息, 立体元图像中的每一个相同位置的像素点则代表了相同角度下的视点图像-子图^[11], 其几何分析过程见图6。

图6

Fig6

	Figure Option ViewDownloadNew Window
	图6 子图像的生成Fig6 Sub-image generation

因此, 可以根据立体元图像与子图像之间映射关系, 利用子图像之间的视差验证所生成立体元图像的正确性。

设显示器的分辨率为1920× 1080, 像素大小为0.25 mm即R_d=1/0.25=4。显示端所用的透镜阵列的孔径P₂=1 mm, 焦距f=5 mm, 显示模式为深度优先模式g₂=5 mm。如果想生成分辨率为50× 50、R_D=1 lpm、视角 θ=12°、立体图像深度Δ Z=150 mm的三维图像, 则由式(1)~(5)可以得到采集端的配置参数为:相机阵列为50× 50; 相机焦距g₁=170 mm; 相机水平和垂直间距分别为Δ x=1 mm, Δ y=1 mm; 渲染分辨率为30× 30。实验的虚拟场景由字母“ JLU” 组成, 其中“ J” 、“ L” 、“ U” 与相机矩阵的距离分别为40、80、20 mm, 如图7所示。利用本文方法可以生成多种孔径透镜阵列所需的立体元图像阵列, 本实验以圆形和方形孔径为例, 分别生成其对应的立体元图像阵列, 透镜阵列如图8所示^[12], P为透镜元间距。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 虚拟场景Fig.7 Virtual scene

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 透镜阵列Fig.8 Lenslet arrays

Maya中虚拟相机阵列与虚拟场景中心的距离为40 mm, 生成的单元图像如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 立体元图像Fig.9 Elemental images

根据像素映射关系(式(6))生成的立体元图像阵列如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 立体元图像阵列Fig.10 Elemental image arrays

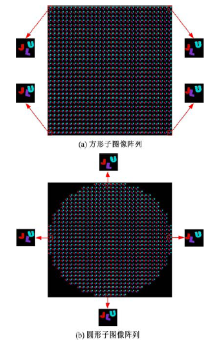
为了验证本文提出的基于Maya的立体元图像的生成方法的正确性, 根据立体元图像与子图间的映射关系, 生成的圆形孔径和方形孔径透镜阵列的子图像阵列, 其分辨率为1500× 1500, 阵列中的每个子图分别代表了不同视角的立体图像显示效果, 分辨率为50× 50, 如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 子图像阵列Fig.11 Sub-image arrays

图11(a)的4个视差图像的坐标分别为(1, 1)、(1, 30)、(30, 1)、(30, 30), 从这4幅视差图中可以看出, (1, 1)与(1, 30)及(30, 1)与(30, 30)之间存在明显的水平视差, 而(1, 1)与(30, 1)及(1, 30)与(30, 30)之间则只有垂直视差。与此同时, 图11(b)的4个视差图像的坐标分别为(15, 1)、(15, 30)、(1, 15)、 (30, 15), 也同样存在水平与垂直方向的视差, 这说明从不同视角观察立体图像, 会看到不同的子图像, 利用本文方法可以生成具有连续视差的圆形与方形孔径透镜阵列的立体元图像阵列。

最后, 为了验证本文方法的正确性, 分别采用真实和虚拟再现的方式重现立体图像。图12为利用透镜阵列直接再现字母“ JLU” , 其显示平台的分辨率为1920× 1080, 微透镜阵列焦距为5 mm, 透镜元间距为1 mm。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 真实再现立体图像Fig.12 True representation of three-dimensional image

图13为计算机虚拟重建不同深度平面下的立体图像。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 计算机虚拟重建立体图像Fig.13 Computer generated three dimensional images

在拍摄过程中, 字母“ JLU” 与相机阵列的距离依次为“ U” 最近, “ J” 居中, “ L” 最远。从计算机虚拟重现立体图像的效果中, 可以看出, 利用本文方法所生成的立体元图像阵列可以重现不同深度平面下的立体图像, 即在20 mm处字母“ U” 最清晰, 40 mm处字母“ J” 最清晰, 80 mm处字母“ L” 最清晰, 这一结果与拍摄场景一致, 因此本文方法是正确有效的。

本文提出了一种基于Maya的立体元图像阵列生成方法, 该方法可以生成多种孔径透镜阵列所需的立体元图像, 与传统利用光学器件生成立体元图像阵列的方法相比, 避免了复杂而繁琐的光学设备校准, 以及硬件设备所带来的误差, 并解决了传统集成成像技术存在空间反转和串扰的问题, 能够准确、高效地生成集成成像技术研究所需的各种图像源。