机电复合传动系统发动机模型集辨识

引用本文

温博轩, 王伟达, 项昌乐, 杨磊, 凌川. 机电复合传动系统发动机模型集辨识. 吉林大学学报（工学版）, 2017, 47(5): 1358-1366
WEN Bo-xuan, WANG Wei-da, XIANG Chang-le, YANG Lei, LING Chuan. Identification of engine model set for electro-mechanical transmission. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1358-1366 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705005
Permissions

机电复合传动系统发动机模型集辨识

温博轩^1,², 王伟达^1,², 项昌乐^1,², 杨磊³, 凌川^1,²

1.北京理工大学机械与车辆学院,北京100081

2.北京理工大学特种车辆研究所,北京100081

3.上汽集团商用车公司技术中心,上海 200438

通信作者:王伟达 (1980-),男,副教授,博士.研究方向:机电复合传动系统控制.E-mail:wangwd0430@163.com

作者简介:温博轩 (1987-),男,博士研究生.研究方向:机电复合传动系统多功率流协同控制.E-mail:wenboxuan258@126.com

基金项目:国家自然科学基金项目(51575043,U1564210)

摘要

通过时域响应试验获得了频域响应所需激励信号的重要参数,设计了频域扫频激励信号。采用扫频激励信号获取发动机的时域辨识数据之后,应用Chirp- z变换来计算对象输入输出信号的离散频谱,进而得到对象的离散频域响应。利用拉盖尔(Laguerre)正交基函数对频域响应进行拟合,利用GA神经网络算法计算对象的频域模型集,给出了柴油发动机数学模型中的不确定性范围,从而建立起发动机带有参数不确定性的动态模型。本文研究为机电复合传动系统的不确定性建模及基于模型的控制打下基础,为功率流鲁棒控制器优化设计提供了依据。

关键词: 车辆工程; 机电复合传动; 发动机模型集; 频域辨识; 扫频设计; 拉盖尔拟合

中图分类号:U469 文献标志码:A 文章编号:1671-5497(2017)05-1358-09

Identification of engine model set for electro-mechanical transmission

WEN Bo-xuan^1,², WANG Wei-da^1,², XIANG Chang-le^1,², YANG Lei³, LING Chuan^1,²

1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081,China

2.National Key Laboratory of Vehicular Transmission, Beijing Institute of Technology, Beijing 100081,China

3.Saic Commercial Vehicle Company Technology Center,Shanghai 200438,China

Abstract

The model based control strategy plays a key role in the power coordinate control. The powers from the electrical and mechanical sources are deeply coupled, and the dynamics of the engine strongly affect the coordinate control. In this paper, sweep signals are used as excitation signals to obtain a frequency domain model set of a class of plants with uncertainties. After collecting data from identification test, the Chirp- z transform is adopted to calculate the discrete frequency spectra of input and output signals. Then, discrete frequency response is obtained. With little priori knowledge of the plant and the type of uncertainties, Laguerre orthogonal basis functions are chosen to construct the nominal frequency domain model. Furthermore, a model set of the plant is determined by using a genetic algorithm, which can depict model errors and some unknown uncertainties. The results are helpful for system analysis and controller design.

Key words: vehicle engineering; electro-mechanical transmission; engine model set; frequency domain identification; sweep signal design; Laguerre fitting

Show Figures

0 引言

混联式混合动力履带车辆的机械动力源部分由发动机、用作电动作用的电机A/B组成, 电动力源则由蓄电池、可用作发电作用的电机A/B组成, 因此又可以称为机电复合传动系统。发动机与电机A/B的不同组合, 可以实现混联式混合动力系统的各种功能; 发动机与系统输出轴解耦, 实现发动机部分脱离实际运行工况单独工作的目的, 进而使得发动机在各种工况下均能保持在高效能的运转区域。为了保证系统的高效率、低消耗运行, 需要对系统进行较为精确的控制。传统的控制大多采用非基于模型的控制^{[1, 2, 3]}, 难以实现更为精确的控制并进一步提升系统性能^[4], Saijad等^{[5, 6]}提出了基于模型的鲁棒控制对系统进行较为精确的控制, 该控制方法在控制器设计时考虑到了模型的不确定性, 使控制器最大范围地适应模型的不确定性。结果表明, 该控制方法对系统性能的提升起到了明显的作用, 其设计过程是基于系统的模型集进行的。

在国内, 清华大学^[7]、东北大学^[8]分别采用基函数拟合法和差值型辨识算法对电动机的模型集进行过辨识, 经过试验验证, 分别得到了接近实际的模型集。在国外, Yoshimura等^[9]、Tadi $\begin{matrix} \overset{'}{c} \end{matrix}$ 等^[10]针对非线性离散系统建模误差以及不确定性干扰的影响, 描述不确定性的范数界, 建立带有参数不确定性及非结构不确定性的系统模型, 基于该模型设计自适应滑模控制, 得到了很好的控制效果。

本文研究对象为机电复合传动系统(EMT), 面向动态控制的过程中系统存在3个输入和3个输出, 属于MIMO系统, 辨识难度增加^[11]。系统存在相对复杂子系统与相对简单子系统, 为了简化辨识过程, 本文采用将整体系统拆分, 分别辨识各子系统的模型, 然后根据各子系统之间的耦合关系, 重新组合各子系统, 进而建立研究对象的带有不确定性的模型集。将系统分为发动机、电机A/B、耦合机构4个子系统。在这些子系统中, 发动机的响应特性对于系统的动力性能及功率流的协同调控具有显著影响, 且模型最为复杂, 因此, 本文将主要针对发动机模型集辨识过程开展研究。利用时域响应, 估计发动机频域响应的激励信号参数, 设计频域激励信号, 作用于发动机, 得到频域响应数据。利用Chirp-z变换计算信号频谱, 进而得到离散频域响应。然后, 利用拉盖尔正交基函数对频域响应进行拟合, 并利用GA神经网络算法计算对象的频域模型集, 建立起发动机带有参数不确定性的动态模型。

1 发动机模型结构确定

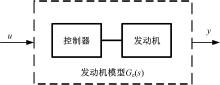
机电复合传动功率流协同调控策略的关注重点为系统的动态的协调过程, 因此需要建立发动机的动态模型集。发动机的动态模型有很多种形式, 如发动机平均值模型、曲轴转矩模型等^{[12, 13, 14, 15]}都能表述发动机的动态特性。本文的研究对象中, 发动机采用转矩控制, 其控制器结构及参数已经确定, 无需再关注发动机内部复杂的物理过程。为了与其他动力源进行协调, 可以将发动机及其控制器(全文将其简称为发动机)归结为一个传递函数形式的黑箱模型, 如图1所示。输入为发动机的目标转矩值T_{e_com}, 输出为发动机的实际转矩值T_{e_act}, 考虑到目标转矩符号的混淆问题, 将发动机控制器接收的转矩指令定义为T_{e_u}。发动机的动态转矩传递函数模型就可以表示为T_{e_act}=G_e(s)· T_{e_u}(s)。发动机的动态建模过程主要为传递函数G_e(s)的辨识过程。

	Figure Option View Download New Window
	图1 发动机黑箱Fig.1 Engine black box

2 激励信号设计与实现

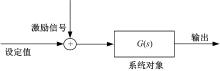
为了获取发动机的动态模型, 采用频域辨识的方法对发动机进行系统辨识, 辨识的框架如图2所示, 对系统施加特殊处理的激励信号, 采集系统的输出数据, 应用特殊算法进行输入输出的频谱分析, 再用相应的函数进行拟合, 即可得到系统的辨识模型^[16]。

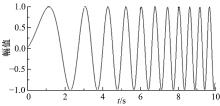
	Figure Option View Download New Window
	图2 系统频域辨识框图Fig.2 Frequency domain identification architecture

激励信号通常使用扫频信号, 它是比较常用的系统辨识输入信号, 典型的扫频信号如图3所示。控制输入决定了系统的输出特性, 即, 决定了系统参数的可辨识性和辨识精度, 所以输入信号设计就成为了系统辨识的基础。辨识混合动力发动机的模型, 需要辨识过程涵盖该发动机的低频和高频特性^[17]。扫频信号的设计主要包含3个方面:扫频信号频率范围的选取、信号调制、信号峰值因数与信号幅值的调整。扫频信号的设计关键在于信号的最小与最大频率的确定, 因此需要对机电复合传动所使用发动机的频带范围有所了解, 确保相干函数和对应的频率响应在应用范围内具有可以接受的精度。

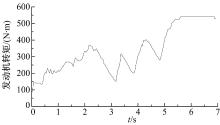
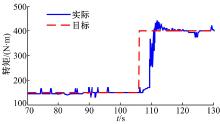
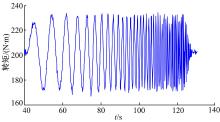
	Figure Option View Download New Window
	图3 典型扫频信号Fig.3 Typical frequency sweep signal

为了确定激励信号的频率范围, 需要估计发动机的带宽, 可以采用时域分析的方法对发动机带宽进行估计。为了更加准确地估计发动机带宽, 对发动机进行多次阶跃响应试验, 尽量广地涵盖发动机转矩波动范围。同时, 也应当联系实际, 发动机转矩值波动比较频繁的区域应当取较多的试验点进行研究。图4为实车试验中发动机的转矩观测值。从图中可以看出, 发动机的转矩在150~450 N· m变换比较频繁, 因此对发动机的阶跃响应试验主要集中在这一转矩范围进行。发动机转矩阶跃响应试验工况参数设定值如表1所示。

	Figure Option View Download New Window
	图4 实车发动机转矩值Fig.4 Engine torque of actual running condition

表1 发动机阶跃响应试验 Table 1 Experiment of engine step response

经过试验, 各组工况得到时域响应的输出结果大抵相同, 不同初始值和调节幅值的阶跃响应具有类似的动态特性。现仅以150~400 N· m的最大范围动态响应为例进行说明, 结果如图5所示。

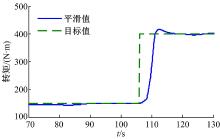
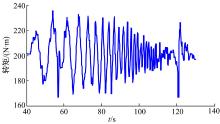
	Figure Option View Download New Window
	图5 发动机阶跃响应试验Fig.5 Step response experiment of engine

经过中值滤波以及平滑处理后, 结果如图6所示。从图6可以得出, 系统响应到达目标值95%的时间约为5.3 s, 根据时域指标与频域指标之间的关系, f(t)=L^-¹[1/(T· s+1)]=1/T· e^-t/T, 可以得出3T≈ 5.3, T≈ 1.8。一阶系统的带宽频率约为1/ω _b, 从而得出ω _b≈ 0.6 rad/s, 从而估计出发动机的带宽频率为ω _b/2π =0.095 Hz。

	Figure Option View Download New Window
	图6 发动机阶跃响应Fig.6 Step response of engine

机电复合传动所用发动机的响应时间常数大概为1.8。为了保证模型在低频段的精度, 同时避免扫频输入周期过长, 指定扫频信号的最小频率为ω _min=0.5 rad/s, 则对应的周期为T_max=2π /ω _min≈ 12 s。最大频率设定至少为带宽的2.5倍, 为了试验数据更广, 可以暂定为15 rad/s, 从而可得出, f_max=15/2π ≈ 2.4 Hz, T_min=1/f_max=0.4。然后确定激励信号包含f_min频率正弦信号的周期个数n₁, 本文取n₁=5, 则单个激励信号扫频记录总长度为T_rec=5T_max=60 s; 试验过程中, 采样时间设置为Δ t=0.01 s, 扫频信号的周期为采样时间的整数倍。f_max的个数为n₂=60/2.4=25, 为整数倍。选取激励信号所包含频率点的频率间隔为Δ f=1/T_rec, 总的频率点个数为n_f=n₂-n₁+1=48-5+1=42。扫频输入信号为:

$δ_{sweep} = Asin (θ (t))$ （1）

$θ (t) = [ω_{\min} - C_{2} (ω_{\max} - ω_{\min})] t + \frac{C_{2} T_{rec}}{C_{1}} (ω_{\max} - ω_{\min}) (e^{(C_{1} t / T_{rec})} - 1)$ （2）

其中取C₁=4, C₂=0.0187, 可满足宽频范围内实际应用的需要。再加入平稳输入与平稳输出, 即可得到本试验所需求的激励信号。幅值A最小需要取最大转矩值的10%才可满足辨识需求。根据图5, 发动机常用转矩范围为250 N· m左右, 因此, 可选择输入最大值为230 N· m, 又发动机转矩不宜过小, 因此最小值选择170 N· m。从而, 获得扫频信号的幅值为A=30。

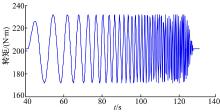
激励信号的时域表示如图7所示。

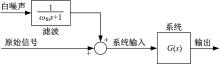
	Figure Option View Download New Window
	图7 激励信号Fig.7 Input signal

仅用上述各式生成的正弦扫频信号有时谱信息不够丰富, 因为在这种信号中不包含输入形状不规则的部分, 而此类不规则成分在人工扫频信号中却实际存在, 另外, 输出信号永远不可能反映出输入信号不包含的频谱特性, 从而导致辨识模型的不准确。因此, 可以在输入信号中加入白噪声信号:

δ _输入=δ _扫频+δ _白噪声

典型的人工噪声的均方根误差为:

δ _白噪声:σ =0.1A_δ

式中:A_δ为信号幅值, 此时信噪比为10。

扫频信号的均方根值为:

δ _扫频= $\begin{matrix} \frac{\sqrt[]{2}}{2} \end{matrix}$ A_δ≈ 0.707A_δ

下面求解白噪声信号的功率谱密度。白噪声信号的均方根值为:

δ _白噪声=0.1δ _扫频=0.0707A_δ

白噪声信号的采样周期(有时也可取为系统采样频率)为:

t_c= $\begin{matrix} \frac{2 π}{100 ω_{\max}} \end{matrix}$

则白噪声信号的功率谱密度(PSD)为:

S= $\begin{matrix} δ_{白噪声}^{2} \end{matrix}$ t_c≈ 0.005 $\begin{matrix} A_{δ}^{2} \end{matrix}$ t_c

白噪声成分应该采用低通滤波器以抑制激励信号中的高频成分, 这里滤波器带宽为:

ω _fn=ω _max

由于滤波器将会滤去部分高频信号, 因此人工噪声信号的均方根值将会减小, 此时应适当增加白噪声信号功率以确保给定的噪声均方根值。

发动机辨识试验的单输入单输出系统辨识实现如图8所示。最终扫频输入的时域信号如图9所示。

	Figure Option View Download New Window
	图8 实际系统输入框图Fig.8 Block diagram of actual system

	Figure Option View Download New Window
	图9 实际扫频输入信号Fig.9 Actual frequency sweep signal

将上述激励信号施加于实际系统, 系统如图10所示。辨识系统主体由发动机、耦合机构、电机组成。发动机与电机经过一级减速后直接相连, 电机充当发动机的负载。系统使用Rapid-ECU作为系统的综合控制单元以及信号采集单元, 通过CAN总线发送控制指令并接收传感器信号。所得试验数据如图11所示。

	Figure Option View Download New Window
	图10 发动机辨识试验台Fig.10 Identification test bench of engine

	Figure Option View Download New Window
	图11 发动机辨识输出数据Fig.11 Output of engine identification

3 采用Chirp-z变换计算对象频率特性

利用上述激励信号完成辨识测试过程并获得试验数据后, 应用Chirp-z变换能准确提取激励信号频谱对应的系统对象频率特性^[15]。与离散傅里叶变换相比, 由时域数据应用Chirp-z变换得到信号频谱时, 在选频上更加灵活。通过Chirp-z变换, 可以从采样数据中得到与激励信号包含相同频率点的信号频谱。离散傅里叶变换在整个z平面单位圆上等间隔取样, 与其相比Chirp-z变换不需要计算系统对象在整个单位圆上z变换的取样, 只需要对信号所在的一段频带进行分析, 并且可以任意选择分辨率, 而以外的部分可不考虑。

Chirp-z变换的表达式为^[7]:

$czt (x (n), N, W, A) = \overset{N - 1}{\sum_{n = 0}} X (N) A W^{- k}, 0 \leq k \leq N - 1$ （3）

式中:x(n)为有限长序列; A=A₀ $\begin{matrix} e^{J θ_{0}} \end{matrix}$ , W=W₀ $\begin{matrix} e^{- J φ_{0}} \end{matrix}$ , A₀为起始取样点在虚平面上的半径长度(通常A₀≤ 1), θ ₀为起始取样点的相角, φ ₀为两相邻点之间的等分角, W₀为螺旋线的伸展率。

辨识过程持续时间为T_rec, 采样时间为Δ t, 则数据点数为N=T_rec· Δ t+1, 变换起始的频率为f_min, A的表达式为:

$\begin{matrix} A = \exp (2 π f_{\min} \cdot Δt \cdot j) (4) \end{matrix}$

设定Chirp-z变换的频率点间隔为Δ f, 计算W的公式为:

$\begin{matrix} W = \exp (- 2 π \cdot j \cdot Δf \cdot Δt) (5) \end{matrix}$

经过Chirp-z变换后, 可以得到输入输出信号离散频谱, 进一步计算, 可以得到对象的离散频率响应为:

$\begin{matrix} H (ω_{k}) = \frac{czt (u, N, W, A)}{czt (y, N, W, A)} (6) \end{matrix}$

式中:ω _k表示对应的频率点。

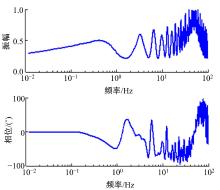
$\begin{matrix} \begin{matrix} ω_{k} = 2 π f_{\min} + (k - 1) \cdot Δf (7) \\ k = 1, 2, \dots, n_{f} \end{matrix} \end{matrix}$

对象的频率特性如图12所示。

	Figure Option View Download New Window
	图12 系统的频率响应Fig.12 Frequency response of system

4 基于拉盖尔正交基函数的辨识

在得到系统的频域响应以后, 需要对其进行已知传递函数的拟合。拟合的方式有很多, 大体都是依据最小二乘法的准则进行。本文选择比较常用的Laguerre正交基函数^[7]对系统模型进行拟合, 通过拟合系统对象的离散频率特性曲线, 并确定基函数系数的上下界参数, 从而确定对象的模型集。Laguerre正交基函数拟合最大的好处是不需要系统的先验知识。

对于任意时标因子p> 0, Laguerre函数时域形式为:

$\begin{matrix} \{\begin{matrix} l_{1} (t) = \sqrt[]{2 p} \cdot e^{- pt} \\ l_{2} (t) = \sqrt[]{2 p} \cdot (- 2 pt + 1) \cdot e^{- pt} \\ ︙ \\ l_{i} (t) = \sqrt[]{2 p} \cdot \frac{e^{pt}}{(i - 1)!} \cdot \frac{d^{i - 1}}{d t^{i - 1}} (t^{i - 1} e^{- 2 pt}) \end{matrix} \end{matrix}$ （8）

式中i=1, 2, …, ¥ ; p为常数, 称为时间比例因子, 或称时标因子; t∈ [0, ¥ )为时间变量。

对式(8)进行Laplace变换, 可得到其频域表达式:

$\begin{matrix} \{\begin{matrix} L_{1} (s) = \int_{0}^{\infty} l_{1} (t) e^{- st} dt = \frac{\sqrt[]{2 p}}{s + p} \\ L_{2} (s) = \int_{0}^{\infty} l_{2} (t) e^{- st} dt = \frac{\sqrt[]{2 p} (s - p)}{{(s + p)}^{2}} \\ ⋮ \\ L_{i} (s) = \int_{0}^{\infty} l_{i} (t) e^{- st} dt = \frac{\sqrt[]{2 p} {(s - p)}^{i - 1}}{{(s + p)}^{i}} \end{matrix} \end{matrix}$ （9）

拉盖尔函数序列构成了L²(R⁺)函数空间上一组完备的归一化正交基, 对于L²(R⁺)上的任意函数都可以展开成Laplace级数形式。假定f(t)为发动机的脉冲响应函数, 由于辨识的为带有发动机控制器的整体模型, 因此, 模型是L₂稳定的, 则有 $\begin{matrix} \int_{0}^{\infty} \end{matrix}$ f²(t)dt< ¥ , 所以, 可以用有限个正交基函数来逼近系统的脉冲响应, 即

$\begin{matrix} f (t) \approx \overset{n}{\underset{i = 1}{\sum c_{i} l_{i} (t)}} \end{matrix}$ (10)

式(10)两边进行拉式变换, 可得频域形式为:

$\begin{matrix} G (s) \approx \overset{n}{\sum_{i = 1}} c_{i} L_{i} (s) \end{matrix}$ (11)

根据对象的实际情况, 确定时标因子p和正交基函数的个数n。令标称模型为:

$\begin{matrix} \begin{matrix} {\tilde{H}}_{0} (ω_{k}) = \overset{n}{\sum_{i = 1}} c_{i} L_{i} (j ω_{k}) = C Θ_{f}^{T} (k) \\ k = 1, 2, \dots, n_{f} \end{matrix} \end{matrix}$ （12）

式中:Θ _j(k)=[L₁(jω _k), L₂(jω _k), …, L_n(jω _k)]; C=[c₁, c₂, …, c_n]。

建立优化模型, 通过优化基函数的系数来拟合真实的频率响应。拟合的目的是使拟合模型的频率响应值接近甚至等于实际系统频率响应值, 频率响应包含幅频、相频特性, 在适应度函数的设定过程中都应当包含。据此, 本文建立适应度函数为:

$f (C) = \overset{n_{f}}{\sum_{k = 1}} [real (H (ω_{k}) - C Θ_{f}^{T} {(k))]}^{2} + \overset{n_{f}}{\sum_{k = 1}} [image (H (ω_{k}) - C Θ_{f}^{T} {(k))]}^{2}$ （13）

正交基函数个数越多, 越能准确地拟合实际频率响应。但是, 大量的正交基函数会造成模型阶数过高等不利影响, 根据经验, 在电机模型中, 分母为8阶时的传递函数模型已经能较好地近似实际系统, 鉴于此, 选择n=8(此时单项基函数分母最高阶为10阶)。时标因子可根据需要拟合的数据的幅值进行选取, 本文取p=1.3。当p=1.3时, 正交基函数的系数应当适当缩小, 因为实际响应数据的幅频特性中, 最大幅值小于1.3, 为了令优化计算尽快收敛, 可取各变量的约束为:

s.t. $\begin{matrix} |C_{i}| \end{matrix}$ ≤ 1

该优化模型中约束条件都为线性, 但考虑到后续模型集的辨识过程含有大量的非线性约束, 而且本文的正交基函数拟合过程需要计算全局最优解, 传统的优化算法(枚举, 启发式等)容易陷入局部极小的误区, 从而出现死循环使迭代无法继续进行。遗传算法是以生物进化为原型, 具有很好的收敛性, 是典型的全局优化算法。同时, 遗传算法又兼具计算时间少、鲁棒性高等明显优点。因此, 本文应用遗传算法求解正交基函数的系数。

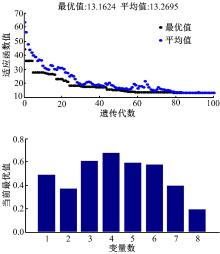
图13为计算过程的进程, 优化在100代结束, 此时适应度函数值的改变低于最小阈值。

	Figure Option View Download New Window
	图13 遗传算法进程Fig.13 Genetic algorithm process

5 计算标称模型及模型集

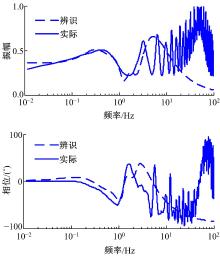
依据上述步骤, 可以得到系统标称模型的频域响应曲线如图14所示。

	Figure Option View Download New Window
	图14 辨识模型频域响应Fig.14 Frequency response of identification model

标称模型的参数值如表2所示。从图14中可以看出, 拟合的系统的幅值和相位与实际系统响应的幅值和相位在低频处十分接近; 在高频处, 系统实际响应震荡非常严重。系统输入的最大频率为15 rad/s, 即2.387 Hz, 因此, 高于此频率的输出并非输入激励所得, 其为干扰项的响应以及噪声的叠加, 不影响辨识准确性。在低频范围内, 发动机系统具有良好的拟合度。

表2 系数值 Table 2 Value of coefficient

标称模型虽然能在一定程度上反映对象的动态特性, 但由于非线性、干扰等不确定性等因素的存在, 标称模型与对象的动态特性之间必然存在不匹配, 进一步建立模型集以描述对象不确定性可能存在的范围更为准确。

利用辨识对象的频域数据, 以及标称模型参数C作为求解模型集上下届参数迭代算法的初值, 应用遗传算法, 确定基函数系数的上、下界C_h、C_l, 从而确定模型集^[7]。

上、下界参数算法分别为:

max $\begin{matrix} \overset{n_{f}}{\sum_{k = 1}} \end{matrix}$ ( $\begin{matrix} |C_{h} Θ_{f}^{T} (k)| \end{matrix}$ - $\begin{matrix} |H (ω_{k})| \end{matrix}$ +ε (k))

s.t. $\begin{matrix} \{\begin{matrix} |C_{h} Θ_{f}^{T} (k)| \geq |H (ω_{k})| + ε (k) \\ c_{i} \leq c_{i}^{h}, i = 1, 2, \dots, n \end{matrix} \end{matrix}$

min $\begin{matrix} \overset{n_{f}}{\sum_{k = 1}} \end{matrix}$ (- $\begin{matrix} |C_{l} Θ_{f}^{T} (k)| \end{matrix}$ + $\begin{matrix} |H (ω_{k})| \end{matrix}$ +ε (k))

s.t. $\begin{matrix} \{\begin{matrix} |C_{l} Θ_{f}^{T} (k)| \leq |H (ω_{k})| + ε (k) \\ c_{i} \geq c_{i}^{l}, i = 1, 2, \dots, n \end{matrix} \end{matrix}$

式中:ε (k)为松弛因子。通过调节松弛因子可以有效剔除频域数据的异常值, 并调节模型集辨识约束条件的强弱。增大松弛因子, 可以得到更小的模型集, 反之, 则获得较大的模型集。经过GA遗传算法计算可以得到模型集的上、下界参数。

6 结果及分析

使用遗传算法计算, 取值p=1.3, N=8可以得到正交基函数的系数及其上、下界的值, 如表2所示。

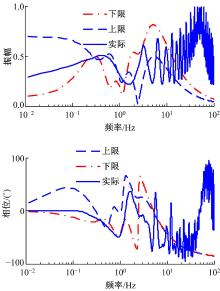
	Figure Option View Download New Window
	图15 辨识模型集响应曲线Fig.15 Frequency response of identification model set

图15为模型集的频率响应特性曲线, 图中幅频和相频特性都能几乎涵盖所有的实际响应曲线, 对系统不确定性进行了较好的描述。

从上述结果可知, 采用扫频激励信号获得辨识数据后, 应用本文给出的辨识方法得到了较好的效果, 其中只需要预先知道对象大致的工作频带, 在没有其他先验知识的情况下, 可以计算出对象的标称模型与模型集, 而无需知道对象极点分布的先验信息。

7 结束语

利用对象时域响应特性估计了系统带宽, 根据该带宽设计了频域激励信号, 给出了利用扫频信号通过台架试验获得辨识数据, 并利用拉盖尔基函数得到对象频域模型集的方法。利用频域辨识, 得到系统频域响应数据, 再利用Chirp-z变换获得对应于特定点的对象频谱信息。然后, 利用Laguerre基函数对响应特性进行拟合, 确定基函数系数的上、下界, 给出系统模型集, 为后续鲁棒控制设计提供了基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Wang Wei-da, Han Li-jin, Xiang Chang-le, et al. Synthetical efficiency-based optimization for the power distribution of power-split hybrid electric vehicles[J]. China Journal of Mechanical Engineering, 2014, 27(1): 58-68. [本文引用:1]
[2]	王伟达, 项昌乐, 韩立金, 等. 基于电池SOC保持的混联式混合动力车辆能量管理策略的研究[J]. 汽车工程, 2011(5): 373-377. Wang Wei-da, Xiang Chang-le, Han Li-jin, et al. A research on SOC retaining-based energy management strategy for PSHEV[J]. Automotive Engineering, 2011(5): 373-377. [本文引用:1]
[3]	秦大同, 杨官龙, 胡明辉, 等. 基于驾驶意图的插电式混合动力汽车能量管理策略[J]. 吉林大学学报: 工学版, 2015, 45(6): 1743-1750. Qin Da-tong, Yang Guan-long, Hu Ming-hui, et al. Energy management strategy of plug-in hybrid eldctric system based on driving intention[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(6): 1743-1750. [本文引用:1]
[4]	林歆悠, 孙东野, 尹燕莉, 等. 基于随机动态规划的混联式混合动力客车能量管理策略[J]. 汽车工程, 2012(9): 830-836. Lin Xin-you, Sun Dong-ye, Yin Yan-li, et al. The energy management strategy for a series-parallel hybrid electric bus based on stochastic dynamic programming[J]. Automotive Engineering, 2012(9): 830-836. [本文引用:1]
[5]	Saijad F, Francis A. The role and use of robust multivariable control in hybrid electric vehicle energy management - part I: an overview[C]//IEEE International Conference on Control Applications, Dubrovnik, Croatia/CCA, 2012: 303-309. [本文引用:1]
[6]	Saijad F, Francis A. The role and use of robust multivariable control in hybrid electric vehicle energy management - part II: application[C]//IEEE International Conference on Control Applications, Dubrovnik, Croatia/CCA, 2012: 317-322. [本文引用:1]
[7]	Dai Yu-ting, Wu Zhi-gang, Yang Chao. Identification for uncertain aeroelastic system set in the frequency domain[C]//The 52nd AIAA/ASME/ASCE/AHS/ASC Structures Structural Dynamics and Materials Conference, Denver, 2011: 1-12. [本文引用:4]
[8]	左义和, 项昌乐, 闫清东, 等. 基于动态规划算法的混联混合动力汽车控制策略[J]. 吉林大学学报: 工学版, 2011, 41(4): 898-903. Zuo Yi-he, Xiang Chang-le, Yan Qing-dong, et al. Parallel-serial hybrid electrical vehicle control strategy based on dynamic programming algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(4): 898-903. [本文引用:1]
[9]	Yoshimura T. Design of a simplified adaptive fuzzy backstepping control for uncertain discrete-time nonlinear systems[J]. International Journal of Systems Science, 2015, 46(5): 763-775. [本文引用:1]
[10]	Tadi xmlns: mml=" M. A novel hybrid MCDM model based on fuzzy DEMATEL, fuzzy ANP and fuzzy VIKOR for city logistics concept selection[J]. Expert Systems with Applications, 2014, 18(41): 8112-8128. [本文引用:1]
[11]	Nema S, Padhy P K. Identification of two-input two-output process using state-space analysis[J]. Control Theory & Application IET, 2015, 13(9): 2029-2036. [本文引用:1]
[12]	Roy I, Robert D. Engine torque ripple cancellation with an integrated starter alternator in a hybrid electric vehicle: implementation and control[J]. IEEE Transactions on Industry Application, 2003, 96(6): 1765-1774. [本文引用:1]
[13]	Cheng A S, Dumitrescu C E, Mueller C J. Investigation of methyl decanoate combustion in an optical direct-injection diesel engine[J]. Energy & Fuels, 2014, 28(12): 3107-3115. [本文引用:1]
[14]	Wu D, Zhou R, Liu M, et al. Numerical investigation of the stability of rotating detonation engines[J]. Combustion Science and Technology, 2014, 108(10/11): 1699-1715. [本文引用:1]
[15]	Hutchins K E, Akella M R, Clemens N T, et al. Experimental identification of transient dynamics for supersonic inlet unstart[J]. Journal of Propulsion and Power, 2014, 30(6): 1605-1612. [本文引用:2]
[16]	Banazadeh A, Gol H A, Ramazani H. Dynamic model identification and control of small turbojet engines using frequency response analysis[C]//International Conference on Advanced Mechatronic Systems, Tokyo, Japan, 2012: 553-558. [本文引用:1]
[17]	Tischler M B, Remple R K. Aircraft and rotorcraft system identification[R]. AIAA Education Series. American Institute of Aeronautics and Astronautics, 2006. [本文引用:1]

2014

0.0

... 传统的控制大多采用非基于模型的控制^[1,2,3],难以实现更为精确的控制并进一步提升系统性能^[4],Saijad等^[5,6]提出了基于模型的鲁棒控制对系统进行较为精确的控制,该控制方法在控制器设计时考虑到了模型的不确定性,使控制器最大范围地适应模型的不确定性 ...

0.0

. , 2011(5):373-377

A research on SOC retaining-based energy management strategy for PSHEV

基于电池SOC保持的混联式混合动力车辆能量管理策略的研究

Wang Wei-da , Xiang Chang-le , Han Li-jin

王伟达, 项昌乐, 韩立金

针对混联式混合动力重型车辆的大驱动功率需求,研究了基于电池SOC保持的能量管理策略.该策略根据保持电池SOC在较高水平的要求进行能量管理与分配,使电池具有较高的功率与能量裕度,从而使电动机可以较大的功率和较长的时间在急加速等大驱动功率需求工况对发动机进行助力,实现重型车辆较高的动力性指标.在此基础上设计了综合控制器并编写了程序代码,采用基于dSPACE的硬件在环仿真系统进行了仿真.结果表明该控制策略在满足燃油经济性和车辆驱动等基本要求的前提下,实现了混联式混合动力车辆能量管理功能与预期的电池SOC保持的目标.

2015

0.0

. 2015, 45(6):1743-1750

Energy management strategy of plug-in hybrid eldctric system based on driving intention

基于驾驶意图的插电式混合动力汽车能量管理策略

Qin Da-tong , Yang Guan-long , Hu Ming-hui

秦大同, 杨官龙, 胡明辉

0.0

. , 2012(9):830-836 DOI:doi:10.3969/j.issn.1000-680X.2012.09.013

The energy management strategy for a series-parallel hybrid electric bus based on stochastic dynamic programming

基于随机动态规划的混联式混合动力客车能量管理策略

Lin Xin-you , Sun Dong-ye , Yin Yan-li

林歆悠, 孙东野, 尹燕莉

针对实际行驶工况中不确定的行驶环境和不同的驾驶员风格等因素对新型混联式混合动力客车燃油经济性的影响,在统计若干城市循环工况数据的基础上建立驾驶员需求功率的马尔科夫模型,提出了一种基于随机动态规划算法的能量管理策略,获得了发动机和电池之间的功率分配控制规则.对新型混联式混合动力客车模型的仿真和硬件在环实验结果表明,所提出的策略能使电池荷电状态在预定的区域内保持平衡,使发动机运行工作点处于高效区域内,且整车100km油耗比原型客车和采用规则控制策略时分别降低了30.17％和11.29％.

2012

0.0

2012

0.0

2011

0.0

... 在国内,清华大学^[7]、东北大学^[8]分别采用基函数拟合法和差值型辨识算法对电动机的模型集进行过辨识,经过试验验证,分别得到了接近实际的模型集 ...

... Chirp-z变换的表达式为^[7]: ...

... 本文选择比较常用的Laguerre正交基函数^[7]对系统模型进行拟合,通过拟合系统对象的离散频率特性曲线,并确定基函数系数的上下界参数,从而确定对象的模型集 ...

... 利用辨识对象的频域数据,以及标称模型参数C作为求解模型集上下届参数迭代算法的初值,应用遗传算法,确定基函数系数的上、下界C_h、C_l,从而确定模型集^[7] ...

2011

0.0

. 2011, 41(4):898-903

Parallel-serial hybrid electrical vehicle control strategy based on dynamic programming algorithm

基于动态规划算法的混联混合动力汽车控制策略

Zuo Yi-he , Xiang Chang-le , Yan Qing-dong

左义和, 项昌乐, 闫清东

2015

0.0

... 在国外,Yoshimura等^[9]、Tadi c'等^[10]针对非线性离散系统建模误差以及不确定性干扰的影响,描述不确定性的范数界,建立带有参数不确定性及非结构不确定性的系统模型,基于该模型设计自适应滑模控制,得到了很好的控制效果 ...

2014

0.0

2015

0.0

... 本文研究对象为机电复合传动系统(EMT),面向动态控制的过程中系统存在3个输入和3个输出,属于MIMO系统,辨识难度增加^[11] ...

2003

0.0

... 发动机的动态模型有很多种形式,如发动机平均值模型、曲轴转矩模型等^{[12,13,14,15]}都能表述发动机的动态特性 ...

2014

0.0

... 发动机的动态模型有很多种形式,如发动机平均值模型、曲轴转矩模型等^{[12,13,14,15]}都能表述发动机的动态特性 ...

2014

0.0

... 发动机的动态模型有很多种形式,如发动机平均值模型、曲轴转矩模型等^{[12,13,14,15]}都能表述发动机的动态特性 ...

2014

0.0

... 发动机的动态模型有很多种形式,如发动机平均值模型、曲轴转矩模型等^{[12,13,14,15]}都能表述发动机的动态特性 ...

... 3 采用Chirp-z变换计算对象频率特性利用上述激励信号完成辨识测试过程并获得试验数据后,应用Chirp-z变换能准确提取激励信号频谱对应的系统对象频率特性^[15] ...

2012

0.0

... 2 激励信号设计与实现为了获取发动机的动态模型,采用频域辨识的方法对发动机进行系统辨识,辨识的框架如图2所示,对系统施加特殊处理的激励信号,采集系统的输出数据,应用特殊算法进行输入输出的频谱分析,再用相应的函数进行拟合,即可得到系统的辨识模型^[16] ...

2006

0.0

... 辨识混合动力发动机的模型,需要辨识过程涵盖该发动机的低频和高频特性^[17] ...