基于焊点参数识别的白车身动态特性

引用本文

杨越东, 陈吉清, 兰凤崇, 周云郊. 基于焊点参数识别的白车身动态特性. 吉林大学学报（工学版）, 2017, 47(5): 1379-1386
YANG Yue-dong, CHEN Ji-qing, LAN Feng-chong, ZHOU Yun-jiao. BIW dynamic characteristics based on spot-welding parameter identification. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1379-1386 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705008
Permissions

基于焊点参数识别的白车身动态特性

杨越东^1,², 陈吉清^1,², 兰凤崇^1,², 周云郊^1,²

1.华南理工大学机械与汽车工程学院,广州 510640

2.广东省汽车工程重点实验室,广州 510640

通信作者:陈吉清(1966-),女,教授,博士生导师.研究方向:车身结构与安全.E-mail:chjq@scut.edu.cn

作者简介:杨越东(1986-),男,博士研究生.研究方向:汽车结构与安全.E-mail:laiwuyyd@126.com

基金项目:广东省科技计划项目(2015B010137002,2014B010106002,2016A050503021)

摘要

推导了焊点质量、刚度矩阵修改与白车身结构动态特性之间的关系,以试验频率与振型为目标,对白车身类板壳点焊结构焊点参数进行识别,提出了利用参数识别的弹塑性梁单元方法对点焊结构进行模拟。与弹塑性梁单元焊点建模方法在动态特性分析方面进行了对比,并应用于实车白车身动态特性仿真进一步验证仿真精度。结果表明,参数识别的弹塑性梁单元焊点建模方法提高了板壳类结构动态特性分析的仿真精度,为点焊的数值模拟仿真提供了一种研究方法。

关键词: 车辆工程; 参数识别; 弹塑性梁单元; 动态特性; 仿真精度

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2017)05-1379-08

BIW dynamic characteristics based on spot-welding parameter identification

YANG Yue-dong^1,², CHEN Ji-qing^1,², LAN Feng-chong^1,², ZHOU Yun-jiao^1,²

1.School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640,China

2.Guangdong Province Key Laboratory of Automotive Engineering, Guangzhou 510640,China

Abstract

The relationship between the modifications of spot-welding mass matrices or rigidity matrices and Body in White (BIW) structural dynamic characteristics is investigated. First, the spot-welding parameters of shell structures in BIW are identified in order to describe the actual structural frequencies and vibration mode. Then, the method of Elastic-Plastic Beam with Parameter Identification (EPBPI) is employed to simulate spot-welding. Finally, the EPBPI method is compared with the universal method of elastic-plastic beam spot-welding in dynamic characteristic analysis, and it is applied to simulate of the dynamic characteristics of a real BIW to further validate the simulation accuracy. Results show that the EPBPI spot-welding simulation method can improve the accuracy of dynamic characteristic simulation of shell structure and provide a research method for spot-welding numerical simulation.

Key words: vehicle engineering; parameters identification; elastic-plastic beam elements; dynamic characteristics; simulation accuracy

Show Figures

0 引言

轿车车身结构主要由薄板冲压的覆盖件、承载骨架和各种加强件组成^[1]。典型的白车身结构一般由3000~5000个焊点焊装而成, 在一条自动生产线上, 每减少一个焊接机器手就意味着生产成本减少3万美元^[2], 因此数量庞大的焊点直接影响焊装时间和生产成本。点焊不仅是汽车制造中的一个重要装配方式, 还与车身结构动态特性、整车NVH性能、碰撞性能中的缓冲吸能、疲劳耐久性以及断裂失效有关。汽车是一种经常处于运动中的特殊结构, 动态特性是其最基本最重要的性能, 如何准确模拟焊接单元对整车模态尤其是对低阶次的整体模态频率计算结果的影响较大^[3]。随着计算机软硬件技术和数值仿真理论的飞速发展, 仿真技术越来越多的作为设计参考依据。因此为车身模型精度至关重要的焊点连接寻找一种准确和有效的模拟方法非常重要, 是确保分析正确的关键因素之一。

对于焊点的模拟, 实体单元、刚性梁单元以及弹塑性梁单元被广泛应用于焊点的仿真。利用实体单元模拟焊点的方法建模时间长, 对数以千计的白车身焊点进行实体单元模拟则白车身模型的自由度将超过数百万, 超出了目前计算机的求解能力^[4]。刚性梁单元模拟方法是利用节点间引入刚性梁的方法进行模拟, 梁单元刚度无法得到控制, 严重依赖网格^{[5, 6, 7]}。利用不依赖于网格的刚性梁单元建模方法, 可以避免网格细化, 节点依赖性降低, 位置精度提高^{[8, 9]}, Matteo等^{[10, 11]}对点焊仿真的处理中利用ACM2单元与CWELD单元进行了比较, 得到了两种单元的模拟精度及其对结构频率的影响, 提出了两种单元的使用准则。利用弹塑性梁单元模拟焊点, 比刚性梁单元模拟焊点的节点依赖性降低, 节点位置精确的前提下通过焊点属性表达焊点的质量、刚度特性^{[3, 12, 13, 14]}。目前利用弹塑性梁单元模拟焊点的方法存在主要的缺陷是焊点属性主要凭借经验设计或者移植相似车型关键部位的相似性进行模拟, 以经验为主的焊点属性不能够正确表达特定性能, 对模拟精度产生严重影响。

本文从结构动态特性出发, 对与动态特性相关的焊点属性进行参数识别, 确定弹塑性梁单元建模方法的焊点参数, 在不增加建模及计算时间的前提下进一步提高了模拟精度。

1 焊点建模参数改变与结构动态特性关系

实际焊点具有一定的质量、刚度特性, 需要根据具体模拟方法按照质量、刚度一致的原则进行确定。为了识别结构动态特性分析中焊点属性建模参数, 推导了焊点属性参数修改与结构动态特性之间的关系。

在多自由度无阻尼振动系统中, 结构动态特性的特征值问题为:

$\begin{matrix} (- ω^{2} [M] + [K]) \{φ\} = \{0\} (1) \end{matrix}$

式中:[M]为总质量矩阵; [K]为总刚度矩阵; ω 为结构各阶次频率; φ 为对应于ω 的特征矢量。

假设仿真分析中某阶次圆频率为ω _s, 相应振型特征矢量为{φ _s}, 公式(1)可以具体化为:

$\begin{matrix} (- ω_{s}^{2} {[M]}_{s} + {[K]}_{s}) \{φ_{s}\} = \{0\} (2) \end{matrix}$

由动态特性试验获得的该阶次圆频率记为ω _t, 相应振型特征矢量为{φ _t}。假设某阶次仿真动态特性需要调整为能够表达实际结构的该阶次实验动态特性, 即某阶次仿真频率ω _s需要被调整为实验频率ω _t, 相应振型{φ _s}与{φ _t}保持一致。为了减少计算量, 仅需计算局部相应的刚度与质量矩阵作微小变动Δ [K]与Δ [M]。实际刚度矩阵[K]_t与质量矩阵[M]_t描述如下:

$\begin{matrix} \begin{matrix} {[K]}_{t} = {[K]}_{s} + Δ [K] (3) \\ {[M]}_{t} = {[M]}_{s} + Δ [M] (4) \end{matrix} \end{matrix}$

利用矩阵特性, 在公式(3)(4)中, 只需求解局部矩阵变量Δ [M]与Δ [M]而不必重新求解整个结构系数矩阵。局部调整后的仿真模型能够表达结构实际动态特性, 具体描述为:

$[({[K]}_{s} + Δ [K]) - ω_{t}^{2} ({[M]}_{s} + Δ [M])] \{φ_{t}\} = \{0\}$ （5）

为了便于分析, 定义频率特性方程α (ω _t)

$\begin{matrix} [α (ω_{t})] = {({[K]}_{s} - ω_{t}^{2} {[M]}_{s})}^{- 1} (6) \end{matrix}$

将公式(6)代入(5)可以得到:

$\begin{matrix} \{φ_{t}\} = [α (ω_{t})] (ω_{t}^{2} Δ [M] - Δ [K]) \{φ_{t}\} (7) \end{matrix}$

假设系统节点i与j间单元质量需要调整δ m_ij, 则Δ [M]=δ m_ij{ $\begin{matrix} ν_{m}^{(ij)} \end{matrix}$ }{ $\begin{matrix} ν_{m}^{(ij)} \end{matrix}$ }^T, 其中{ $\begin{matrix} ν_{m}^{(ij)} \end{matrix}$ }=(0, 0, …, $\begin{matrix} \underset{ij}{1} \end{matrix}$ , …, 0)^T。同理, 如果i与j间单元刚度需要调整δ k_ij, 则Δ [K]=δ k_ij{ $\begin{matrix} ν_{n}^{(ij)} \end{matrix}$ }{ $\begin{matrix} ν_{n}^{(ij)} \end{matrix}$ }^T, 其中{ $\begin{matrix} ν_{n}^{(ij)} \end{matrix}$ }=(0, 0, …, $\begin{matrix} \underset{ij}{1} \end{matrix}$ , …, 0)^T。

如果需要调整的质量与刚度单元总数分别为m与n。公式(7)能够被改写为:

$\{φ_{t}\} = [α (ω_{t})] (ω_{t}^{2} \overset{m}{\sum_{i = 1}} δ m_{ij} \{ν_{m}^{(ij)}\} {\{ν_{m}^{(ij)}\}}^{T} - \overset{n}{\sum_{i = 1}} δ k_{ij} \{ν_{n}^{(ij)}\} {\{ν_{n}^{(ij)}\}}^{T}) \{φ_{t}\} =$

$[α (ω_{t})] (ω_{t}^{2} \overset{m}{\sum_{i = 1}} δ m_{ij} \{ν_{m}^{(ij)}\} {\{ν_{m}^{(ij)}\}}^{T}) \{φ_{t}\} - [α (ω_{t})] (\overset{n}{\sum_{i = 1}} δ k_{ij} \{ν_{n}^{(ij)}\} {\{ν_{n}^{(ij)}\}}^{T}) \{φ_{t}\}$ (8)

公式(8)中前半部分仅对m组节点对应的单元质量进行调整, 后半部分对n组节点对应的单元刚度进行调整。

(1)仅对n组节点对应的单元刚度进行调整时, 调整部分的振型特征向量{φ _t}以及相应的该阶次圆频率ω _t可以具体表示为{ $\begin{matrix} X_{ij}^{*} \end{matrix}$ , $\begin{matrix} X_{jk}^{*} \end{matrix}$ , …, $\begin{matrix} X_{ni}^{*} \end{matrix}$ }^T, 共n个具体单元变量。将有限元中的节点矩阵转化为单元矩阵。频率特性变换函数α _pq_,_rs(ω _t)及模态振型变换向量{φ _t}为^[15]:

$\begin{matrix} \begin{matrix} \{\begin{matrix} X_{ij}^{*} = X_{i}^{*} - X_{j}^{*} \\ X_{jk}^{*} = X_{j}^{*} - X_{k}^{*}, \dots, X_{ni}^{*} = X_{n}^{*} - X_{i}^{*} \end{matrix} (9) \\ α_{pq, rs} (ω_{t}) = α_{pr} (ω_{t}) + α_{qs} (ω_{t}) - α_{ps} (ω_{t}) - α_{qr} (ω_{t}) (10) \end{matrix} \end{matrix}$

频率特性函数矩阵 $\begin{matrix} [α (ω_{t})] \end{matrix}$ 可以以单元的形式具体表示如下:

$\begin{matrix} [\begin{matrix} α_{ij, ij} (ω_{t}) & α_{ij, jk} (ω_{t}) & \dots & α_{ij, ni} (ω_{t}) \\ α_{jk, ij} (ω_{t}) & α_{jk, jk} (ω_{t}) & \dots & α_{jk, ni} (ω_{t}) \\ ⋮ & ⋮ & ⋮ \\ α_{ni, ij} (ω_{t}) & α_{ni, jk} (ω_{t}) & \dots & α_{ni, ni} (ω_{t}) \end{matrix}] \end{matrix}$

因此, 公式(8)通过一系列改变能够变换为:

${\{X_{ij}^{*}, X_{jk}^{*}, \dots, X_{ni}^{*}\}}^{T} = - [\begin{matrix} α_{ij, ij} (ω_{t}) & α_{ij, jk} (ω_{t}) & \dots & α_{ij, ni} (ω_{t}) \\ α_{jk, ij} (ω_{t}) & α_{jk, jk} (ω_{t}) & \dots & α_{jk, ni} (ω_{t}) \\ ⋮ & ⋮ & ⋮ \\ α_{ni, ij} (ω_{t}) & α_{ni, jk} (ω_{t}) & \dots & α_{ni, ni} (ω_{t}) \end{matrix}] \times [\begin{matrix} δ k_{ij} \\ δ k_{jk} \\ ⋱ \\ δ k_{ni} \end{matrix}] {\{X_{ij}^{*}, X_{jk}^{*}, \dots, X_{ni}^{*}\}}^{T}$ （11）

该方程通解为:

$- α_{ij, ij} (ω_{t}) δ k_{ij} X_{ij}^{*} - α_{ij, jk} (ω_{t}) δ k_{jk} X_{jk}^{*} - \dots - α_{ij, ni} (ω_{t}) δ k_{ni} X_{ni}^{*} = X_{ij}^{*}$ （12）

当仅调整节点i与j间单元刚度时, 则δ k_jk=0, …, δ k_ni=0, 公式(12)转变为:

$\begin{matrix} δ k_{ij} = - \frac{1}{α_{ij, ij} (ω_{t})} \end{matrix}$ （13）

(2)同理, m个单元局部质量矩阵需要调整时的通解推导可以得到:

$ω_{t}^{2} [α_{ij, ij} (ω_{t}) δ m_{ij} X_{ij}^{*} + α_{ij, jk} (ω_{t}) δ m_{jk} X_{jk}^{*} + \dots + α_{ij, mi} (ω_{t}) δ k_{mi} X_{mi}^{*}] = X_{ij}^{*}$ （14）

当仅调整节点i与j间单元刚度时, 则

$\begin{matrix} δ m_{ij} = \frac{1}{α_{ij, ij} (ω_{t})} \cdot \frac{1}{ω_{t}^{2}} \end{matrix}$ （15）

特解公式(13)或(15)得到了仅通过调整节点i与j间单元刚度或者质量的调整量, (12)或(14)得到了通过调整局部n个或者m个单元刚度矩阵或者质量矩阵的调整量。得到了实际焊点等连接关系刚度、质量属性参数与结构动态特性的关系, 为参数识别中参数的选取提供了理论依据。

2 焊点属性参数识别

2.1 点焊结构模态分析实验

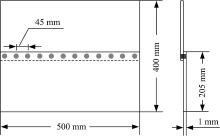
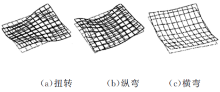
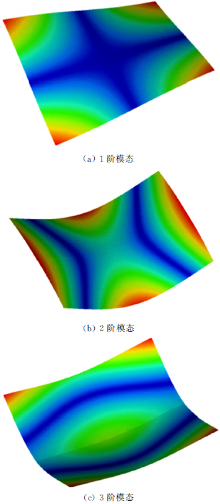
高书娜等^[4]利用两块1 mm钢板, 以45 mm间距搭接点焊连接, 进行模态实验研究。实验前三阶模态值如表1所示, 实验用钢板几何模型及实验模态振型图如图1、图2所示。

表1 实验模态频率 Table 1 Experimental modal frequencies

	Figure Option View Download New Window
	图1 点焊钢板几何模型Fig.1 Geometric model for spot-welding plate

	Figure Option View Download New Window
	图2 实验模态振型图Fig.2 Vibration modes for experimental modal

	Figure Option View Download New Window
	图3 刚性梁单元模型Fig.3 Rigid beam element model

2.2 参数识别

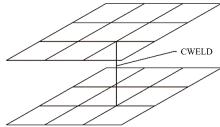
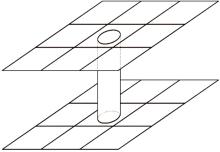
对于目前普遍采用的刚性梁单元, 其有限元模型可以用图3示意, 上下两层板壳单元中间部分代表了1D刚性梁单元。在此理想化的刚体假设中, 刚性梁不具有质量、弹塑性等属性, 刚性梁单元上任意两点间相对位移不变(没有形变), 相当于两个节点刚性耦合共节点。逐步发展的弹塑性梁单元模型, 可以用图4示意, 梁单元上不同位置处受力大小不同, 在力的作用下焊点发生弹塑性形变, 能够在达到极限的情况下模拟焊点失效, 更符合实际受力情况。

	Figure Option View Download New Window
	图4 弹塑性梁单元模型Fig.4 Elastic-plastic beam element model

由于点焊过程中, 焊点的尺寸误差和焊点周围的接触应力等不确定因素对结构整体性能影响很大。而弹塑性梁单元模拟过程中依旧采用原始焊点尺寸等属性参数或者采用经验值, 这使得点焊模拟过程中误差变大。在重点考虑结构动态特性的数值仿真中, 提出了对焊点模拟的尺寸及弹性阶段属性参数进行多目标等效识别, 以完善弹塑性梁模拟焊点方法, 提高仿真精度。

通解方程(14)与(16)从理论上阐明了通过调节局部需要调节的质量与刚度矩阵可以达到仿真结果能够正确描述结构实际动态特性的原因。通解方程的真实值通常是不可能准确获得的, 因此一些混合近似算法经常被用来节约计算时间尽量获得近似真实的值。CA或IC算法是求解局部修改重分析问题的核心, 比如在拓扑优化中各迭代步的结构修改中。这些方法会依赖于初始值, 因此初始值决定了求解结果的正确与否^[16]。自适应多种群的遗传算法(AMGA)扩展了搜索空间, 自适应地调整多个种群的运行状态, 选择的特征数量较少、分类精度较高, 可广泛应用于特征选择领域, 有效地控制了标准遗传算法早熟收敛和局部搜索能力弱的缺点, 应用于特征选择处理, 从多维特征集合中寻找最优的特征子集^[17]。因此, 将模态实验数据作为目标, 利用AMGA算法准确高效地识别了白车身类板壳结构的结构动态特性仿真中焊点的刚度、质量矩阵属性参数。

焊点质量矩阵的识别通过单元属性中的密度与焊点直径调整来完成。焊点刚度矩阵的识别通过单元属性中的弹性模量与泊松比调整来提高动态特性仿真的精度。因此本文以单元弹性模量E、泊松比μ 、焊点直径D、密度ρ 作为待识别参数变量, 前3阶模态频率值M₁、M₂、M₃作为目标, 在Isight软件中运用自适应多种群的遗传算法(AMGA)执行500次计算。获得了变量的进化Pareto解集如表2所示, 其中第108次求解即进化解集中的第10步的结果达到收敛, 是推荐的考虑结构动态特性白车身焊点属性建模弹性模量、泊松比、焊点直径最合适的解。识别了焊点仿真参数, 变量的进化迭代收敛过程如图5所示。

定义多目标参数识别问题数学表达式为:

Target f_m $\begin{matrix} (x) \end{matrix}$ =T_m

$\begin{matrix} X_{i}^{(L)} \end{matrix}$ ≤ X_i≤ $\begin{matrix} X_{i}^{(U)} \end{matrix}$ i=1, 2, …, n

式中:X_i为第i个设计变量; n为设计变量的总数, 本文中n=3; $\begin{matrix} X_{i}^{(L)} \end{matrix}$ 和 $\begin{matrix} X_{i}^{(U)} \end{matrix}$ 分别代表第i个设计变量取值的上限和下限; f_m(x)为第m个子目标函数, m为目标函数的总数, 本文m=3。

表2 进化的Pareto解集 Table 2 Improvement Pareto solutions

	Figure Option View Download New Window
	图5 变量的进化迭代收敛过程Fig.5 Improvement iterative procedure for variables

	Figure Option View Download New Window
	图6 参数识别的弹塑性梁单元模拟焊点方法前3阶模态Fig.6 The lowest 3 orders modal of parameters identification

3 计算实例

分别利用经验弹塑性梁单元建模方法与参数识别的弹塑性梁单元建模方法对焊点1mm钢板结构进行模态分析, 得到结构频率特征值与振型图, 其中图6列出了本文提出的参数识别的弹塑性梁单元模拟焊点方法的前3阶频率值及振型。

文献中应用的刚性梁单元模拟方法、经验弹塑性梁单元建模方法与参数识别的弹塑性梁单元建模方法前3阶模态的振型没有发生变化, 与实验模态一致; 3种建模方法的分析模态与实验模态的相对误差最大值从经验参数的3.66%, 刚性梁模拟的-2.76%降低为1.68%, 相对误差的范围从刚性梁的-2.76%~2.10%, 经验值的-0.95%~3.66%变为-1.93%~1.68%, 相对误差范围变小, 在试验模态值附近的波动变小。经过参数识别后的频率值更接近真实的实验频率, 仿真的准确度得到提高, 表3对各阶频率值及相对误差作了详细对比。

4 实例车型

对某轿车白车身进行模态实验, 实验模态频率值及各阶模态振型如图7所示。将本文得到的焊点模拟参数识别值代入实车白车身有限元模型, 进行模态分析与对比验证。

	Figure Option View Download New Window
	图7 实车白车身前3阶模态及频率值Fig.7 The lowest three orders modal of a real BIW

	Figure Option View Download New Window
	图8 白车身前3阶分析模态Fig.8 The lowest 3 orders analysis modal

	Figure Option View Download New Window
	图9 刚性梁焊点模型响应点特性Fig.9 Response point characteristics in rigid model

对参数识别弹塑性梁单元焊点建模方法与该白车身CAE部门经验值建模方法的分析模态进行对比, 其中前3阶模态频率值及振型图如图8所示。对前3阶模态进行详细对比如表4所示。可以得出, 利用参数识别的弹塑性梁单元法模拟得到的振型较经验法得到的振型更加光顺平滑, 与实验振型更接近; 与实验模态的相对误差最大值从经验值法的10.1%降低为-7.2%, 前3阶模态相对误差明显得到改善。综合分析, 参数识别的弹塑性梁单元法能够更准确有效地表达白车身结构的动态特性, 得到的振型与参数识别前振型相比更接近实验模态振型。

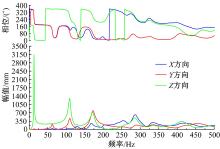
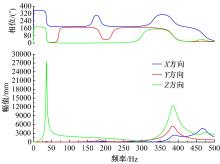
对该白车身进行了扭转工况下的0~500 Hz单位激励频响分析, 比较了同激励同响应点的加速度特性。如图9、10所示, 对应相位发生180° 突变的位置为白车身的一个主要振型, 通常在60 Hz低频范围内可以找出符合条件的振型, 对应模态分析振型, 可以得到一阶弯曲或者一阶扭转振型。

工程中常用的刚性梁单元仿真焊点在频响分析中得到模型一阶频率为13 Hz, 对应响应点振动加速度大小为0.32 g(g=9.8 m/s²); 在参数识别后的弹塑性梁单元仿真焊点分析中, 一阶频率为37 Hz与自由模态得到的结构固有频率37.6 Hz基本吻合, 对应响应点振动加速度大小为2.80 g(g=9.8 m/s²), 响应点频率大小及加速度峰值均比刚性梁单元方法模拟焊点更接近实际情况。

表3 三种焊点建模方法模态对比 Table 3 Comparisons of three spot-welding modeling methods

表4 白车身实验模态与分析模态对比 Table 4 Comparison of analysis and experimental modal

	Figure Option View Download New Window
	图10 参数识别的弹塑性梁焊点模型响应点特性Fig.10 Response point characteristics in elastic-plastic model

5 结束语

考虑弹塑性梁焊点建模方法中属性参数与白车身类板壳结构动态特性之间的关系, 确定了待识别参数。利用自适应多种群的遗传算法(AMGA)识别了弹塑性梁单元方法中焊点属性参数。解决了现有的弹塑性梁单元模拟焊点利用焊点区域参数或者经验参数致使动态特性模拟精度不足甚至出现大于10%误差的错误。辨识了与动态特性相关的弹性阶段焊点属性参数的10组改进解集, 并利用其中一组最优解集进行了实车白车身点焊结构动态特性模拟, 验证了参数识别的弹塑性梁单元焊点建模方法能够更准确地模拟结构动态特性, 提高仿真精度。为进一步研究焊点塑性阶段失效、断裂等特性属性识别提供了参考依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张洪欣. 汽车设计[M]. 北京: 机械工业出版社, 1995. [本文引用:1]
[2]	叶远林. 轿车设计中的焊点疲劳寿命预测方法[J]. 计算机辅助工程, 2006, 15(B09): 189-192. Ye Yuan-lin. Method for fatigue life prediction of sutomotive spot-welds[J]. Computer Aided Engineering, 2006, 15(B09): 189-192. [本文引用:1]
[3]	宋海生, 史文库, 龙岩, 等. 整车模态分析中焊点模拟方法的研究[J]. 汽车工程, 2011, 33(11): 920-923. Song Hai-sheng, Shi Wen-ku, Long Yan, et al. A study on spot-weld modeling in vehicle modal analysis[J]. Automotive Engineering, 2011, 33(11): 920-923. [本文引用:2]
[4]	高书娜, 邓兆祥, 胡玉梅. 车身点焊连接有限元模拟方法研究[J]. 汽车工程, 2008, 30(9): 811-815. Gao Shu-na, Deng zhao-xiang, Hu Yu-mei. A study on the finite element modeling for spot-welds of vehicle body[J]. Automotive Engineering, 2008, 30(9): 811-815. [本文引用:2]
[5]	孙凌玉, 谢军, 于春生, 等. 汽车车身结构动力学建模方法研究[J]. 机械工程学报, 1999, 35(5): 72-74. Sun Ling-yu, Xie Jun, Yu Chun-sheng, et al. Study on dynamic modeling of automobile body structure[J]. Chinese Journal of Mechanical Engineering, 1999, 35(5): 72-74. [本文引用:1]
[6]	Dooms D, Degrand e G, De Roeck G, et al. Finite element modeling of a silo based on experimental modal analysis[J]. Engineering Structures, 2006, 28(4): 532-542. [本文引用:1]
[7]	何文, 张为刚, 钟志华. 汽车碰撞仿真研究中点焊连接关系的有限元模拟[J]. 机械工程学报, 2005, 41(9): 73-77. He Wen, Zhang Wei-gang, Zhong Zhi-hua. Finite element modeling of spot-welding dynamic simulation of automobiles[J]. Chinese Journal of Mechanical Engineering, 2005, 41(9): 73-77. [本文引用:1]
[8]	何文, 张为刚, 钟志华. 汽车动态仿真中车身点焊有限元建模的新方法[J]. 汽车工程, 2006, 28(1): 81-84. He Wen, Zhang Wei-gang, Zhong Zhi-hua. New finite element modeling technique for spot-welds of autobody in vehicle dynamic simulation[J]. Automotive Engineering, 2006, 28(1): 81-84. [本文引用:1]
[9]	Xu S, Deng X. An evaluation of simplified finite element models for spot-welded joints[J]. Finite Elements in Analysis and Design, 2004, 40(9): 1175-1194. [本文引用:1]
[10]	Matteo Palmonella, Michael I Friswell, John E Mottershead, et al. Guidelines for the implementation of the CWELD and ACM2 spot weld models in structural dynamics[J]. Finite Element in Analysis and Design, 2004, 41(2): 193-210. [本文引用:1]
[11]	Matteo Palmonella, Michael I Friswell, John E Mottershead, et al. Finite element models of spot welds in structural dynamics: review and updating[J]. Computers and Structures, 2005, 83(8-9): 648-661. [本文引用:1]
[12]	王登峰, 张斌, 陈静, 等. 商用车驾驶室白车身焊点缩减拓扑优化研究[J]. 汽车工程, 2009, 31(4): 326-330. Wang Deng-feng, Zhang Bin, Chen Jing, et al. A study on topology optimization for the cab BIW of a vommercial vehicle aiming at welding spot reduction[J]. Automotive Engineering, 2009, 31(4): 326-330. [本文引用:1]
[13]	于多年, 邹骥, 王登峰, 等. 重型卡车驾驶室焊点的拓扑优化分析[J]. 吉林大学学报: 工学版, 2009, 39(2): 264-268. Yu Duo-nian, Zou Ji, Wang Deng-feng, et al. Analysis of topological optimization on optimal heavy truck cab's spot-weld layout[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(2): 264-268. [本文引用:1]
[14]	施欲亮, 朱平, 沈利冰, 等. 基于汽车碰撞仿真的点焊连接关系有限元模拟方法[J]. 机械工程学报, 2007, 43(7): 226-230. Shi Yu-liang, Zhu Ping, Shen Li-bing, et al. Finite element modeling of spot welds based on vehicle impact[J]. Chinese Journal of Mechanical Engineering, 2007, 43(7): 226-230. [本文引用:1]
[15]	Zhang X C, Sun G Z. A modal approximation method of frequency modification[C]//Proceedings of the Asia-Pacific Vibration Conference, 1993: 402-408. [本文引用:1]
[16]	Bogomolny M. Topology optimization for free vibrations using combined approximations[J]. International Journal for Numerical Methods in Engineering, 2010, 82(5): 617-636. [本文引用:1]
[17]	刘元宁, 王刚, 朱晓冬, 等. 基于自适应多种群遗传算法的特征选择[J]. 吉林大学学报: 工学版, 2011, 41(6): 1690-1693. Liu Yuan-ning, Wang Gang, Zhu Xiao-dong, et al. Feature selection based on adaptive multi-population genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(6): 1690-1693. [本文引用:1]

1995

0.0

... 0 引言轿车车身结构主要由薄板冲压的覆盖件、承载骨架和各种加强件组成^[1] ...

2006

0.0

. 2006, 15(B09):189-192 DOI:doi:10.3969/j.issn.1006-0871.2006.z1.062

Method for fatigue life prediction of sutomotive spot-welds

轿车设计中的焊点疲劳寿命预测方法

Ye Yuan-lin.

叶远林

An engineering calculation method of spot weld fatigue life prediction is introduced.The method applies the CWELD element to simulate the weld nugget and the shell element to simulate the sheet metal and uses the bar element cross sectional forces and moments to calculate the "structural stresses" in each spot-weld nugget and the adjacent sheets.These stresses are then used to make fatigue life predictions on the spot weld using the S-N curves method.From the analysis the fatigue lives and the locations of spot-welds can be predicted and the weak area of BIW can be found.

介绍一种焊点疲劳寿命预测的工程计算方法.用有限元分析中的CWELD单元模拟焊核,用壳单元模拟连接板,根据CWELD单元传递力和力矩计算焊核附近连接板和焊核周围的“结构应力”；然后通过一组焊点S―N 曲线估计焊点的疲劳寿命.通过分析预测焊点疲劳寿命以及相应位置,发现白车身薄弱环节.

... 典型的白车身结构一般由3000~5000个焊点焊装而成,在一条自动生产线上,每减少一个焊接机器手就意味着生产成本减少3万美元^[2],因此数量庞大的焊点直接影响焊装时间和生产成本 ...

2011

0.0

. 2011, 33(11):920-923

A study on spot-weld modeling in vehicle modal analysis

整车模态分析中焊点模拟方法的研究

Song Hai-sheng , Shi Wen-ku , Long Yan

宋海生, 史文库, 龙岩

针对整车有限元模态分析中,采用刚性梁单元模拟焊点时刚度无法控制和严重依赖网格的弊端,提出采用弹塑性梁单元模拟焊点的方法.以某轻型客车为例,建立整车有限元模型,分别采用上述两种单元模拟焊点进行模态分析.与试验结果的对比表明,整车模态分析中采用弹塑性梁单元模拟焊点的方法更接近试验结果,即更为准确、有效.

... 汽车是一种经常处于运动中的特殊结构,动态特性是其最基本最重要的性能,如何准确模拟焊接单元对整车模态尤其是对低阶次的整体模态频率计算结果的影响较大^[3] ...

... 利用弹塑性梁单元模拟焊点,比刚性梁单元模拟焊点的节点依赖性降低,节点位置精确的前提下通过焊点属性表达焊点的质量、刚度特性^[3,12,13,14] ...

2008

0.0

. 2008, 30(9):811-815

Deng zhao-xiang, Hu Yu-mei. A study on the finite element modeling for spot-welds of vehicle body

车身点焊连接有限元模拟方法研究

Gao Shu-na

高书娜, 邓兆祥, 胡玉梅

... 利用实体单元模拟焊点的方法建模时间长,对数以千计的白车身焊点进行实体单元模拟则白车身模型的自由度将超过数百万,超出了目前计算机的求解能力^[4] ...

... 1 点焊结构模态分析实验高书娜等^[4]利用两块1 mm钢板,以45 mm间距搭接点焊连接,进行模态实验研究 ...

1999

0.0

... 刚性梁单元模拟方法是利用节点间引入刚性梁的方法进行模拟,梁单元刚度无法得到控制,严重依赖网格^[5,6,7] ...

2006

0.0

... 刚性梁单元模拟方法是利用节点间引入刚性梁的方法进行模拟,梁单元刚度无法得到控制,严重依赖网格^[5,6,7] ...

2005

0.0

. 2005, 41(9):73-77

Finite element modeling of spot-welding dynamic simulation of automobiles

汽车碰撞仿真研究中点焊连接关系的有限元模拟

He Wen , Zhang Wei-gang , Zhong Zhi-hua.

何文, 张为刚, 钟志华

... 刚性梁单元模拟方法是利用节点间引入刚性梁的方法进行模拟,梁单元刚度无法得到控制,严重依赖网格^[5,6,7] ...

2006

0.0

. 2006, 28(1):81-84 DOI:doi:10.3321/j.issn:1000-680X.2006.01.020

New finite element modeling technique for spot-welds of autobody in vehicle dynamic simulation

汽车动态仿真中车身点焊有限元建模的新方法

He Wen , Zhang Wei-gang , Zhong Zhi-hua.

何文, 张为刚, 钟志华

对点焊连接提出了一种新的模拟技术,即不同于传统的节点对节点模拟焊接.新型焊接单元在有限元节点与单元之间引入一短梁单元来模拟焊接关系,单元承受拉伸力和剪切力.仿真实例说明,此新型焊接单元,既保证了仿真计算的可靠,又避免了传统算法中细化局部网格的处理,减轻了工作量.

... 利用不依赖于网格的刚性梁单元建模方法,可以避免网格细化,节点依赖性降低,位置精度提高^[8,9],Matteo等^[10,11]对点焊仿真的处理中利用ACM2单元与CWELD单元进行了比较,得到了两种单元的模拟精度及其对结构频率的影响,提出了两种单元的使用准则 ...

2004

0.0

2004

0.0

2005

0.0

2009

0.0

. 2009, 31(4):326-330 DOI:doi:10.3321/j.issn:1000-680X.2009.04.008

A study on topology optimization for the cab BIW of a vommercial vehicle aiming at welding spot reduction

商用车驾驶室白车身焊点缩减拓扑优化研究

Wang Deng-feng , Zhang Bin , Chen Jing

王登峰, 张斌, 陈静

为某一商用车驾驶室白车身建立了以固有频率为约束条件,焊点体积最小化为目标的优化模型.利用有限元法进行结构拓扑优化,根据灵敏度分析得到的每个单元对结构性能的贡献来决定有限元单元的保留或删除.通过拓扑优化,驾驶室白车身焊点数目大幅度减少,获得了满足设计要求的焊点的重新分布.对比优化前后仿真分析结果表明,文中所建模型及分析方法是合理而有效的.

... 利用弹塑性梁单元模拟焊点,比刚性梁单元模拟焊点的节点依赖性降低,节点位置精确的前提下通过焊点属性表达焊点的质量、刚度特性^[3,12,13,14] ...

2009

0.0

. 2009, 39(2):264-268

Analysis of topological optimization on optimal heavy truck cab's spot-weld layout

重型卡车驾驶室焊点的拓扑优化分析

Yu Duo-nian , Zou Ji , Wang Deng-feng

于多年, 邹骥, 王登峰

... 利用弹塑性梁单元模拟焊点,比刚性梁单元模拟焊点的节点依赖性降低,节点位置精确的前提下通过焊点属性表达焊点的质量、刚度特性^[3,12,13,14] ...

2007

0.0

. 2007, 43(7):226-230 DOI:doi:10.3321/j.issn:0577-6686.2007.07.040

Finite element modeling of spot welds based on vehicle impact

基于汽车碰撞仿真的点焊连接关系有限元模拟方法

Shi Yu-liang , Zhu Ping , Shen Li-bing

施欲亮, 朱平, 沈利冰

针对现在一般汽车碰撞有限元模型采用刚性梁作为点焊连接关系的模拟方法,通过仿真计算和参数影响分析,发现网格大小以及刚性梁与相连平面的夹角对于点焊的失效时间有着很大的影响,采用刚性梁单元模拟点焊连接关系是不稳定、不可靠的.提出以不依赖网格节点的弹--塑性梁作为点焊连接的有限元模拟方法,并经过仿真结果对比,发现弹--塑性梁单元对小网格尺寸不敏感,对于点焊失效时间的模拟是稳定、可靠的,因而更加适合在汽车碰撞仿真中对点焊连接关系进行模拟.

... 利用弹塑性梁单元模拟焊点,比刚性梁单元模拟焊点的节点依赖性降低,节点位置精确的前提下通过焊点属性表达焊点的质量、刚度特性^[3,12,13,14] ...

1993

0.0

... _t}为^[15]: ...

2010

0.0

... 这些方法会依赖于初始值,因此初始值决定了求解结果的正确与否^[16] ...

2011

0.0

. 2011, 41(6):1690-1693

Feature selection based on adaptive multi-population genetic algorithm

基于自适应多种群遗传算法的特征选择

Liu Yuan-ning , Wang Gang , Zhu Xiao-dong

刘元宁, 王刚, 朱晓冬

摘　要：针对标准遗传算法早熟收敛和局部搜索能力弱的缺点,提出了一种自适应多种群的遗传算法（AMGA）,包含了多种群规划模型（MPP）和动态选择操作算法（DSA）,应用于特征选择处理,从多维特征集合中寻找最优的特征子集。该方法扩展了搜索空间,自适应地调整多个种群的运行状态,有效地控制早熟收敛,增强了局部搜索能力。最后,将本文方法与标准遗传算法的试验结果进行比较,表明本文算法选择的特征数量较少、分类精度较高,可广泛应用于特征选择领域。

... 自适应多种群的遗传算法(AMGA)扩展了搜索空间,自适应地调整多个种群的运行状态,选择的特征数量较少、分类精度较高,可广泛应用于特征选择领域,有效地控制了标准遗传算法早熟收敛和局部搜索能力弱的缺点,应用于特征选择处理,从多维特征集合中寻找最优的特征子集^[17] ...