基于车道选择特性的环形交叉口行程时间预测

引用本文

李志慧, 汪昆维, 宋现敏, 刘鑫山, 谌垚, 罗瑞琪. 基于车道选择特性的环形交叉口行程时间预测. 吉林大学学报（工学版）, 2017, 47(5): 1411-1419
LI Zhi-hui, WANG Kun-wei, SONG Xian-min, LIU Xin-shan, SHEN Yao, LUO Rui-qi. Roundabout travel time prediction based on characteristics of lane choosing. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1411-1419 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705012
Permissions

基于车道选择特性的环形交叉口行程时间预测

李志慧, 汪昆维, 宋现敏, 刘鑫山, 谌垚, 罗瑞琪

吉林大学交通学院,长春 130022

通信作者:宋现敏(1978-),女,副教授,博士.研究方向:交通控制,交通流理论.E-mail:songxm@jlu.edu.cn

作者简介:李志慧(1977-),男,副教授,博士.研究方向:视频检测.E-mail:lizhih@jlu.edu.cn

基金项目:国家自然科学基金项目(51278220,51278520)

摘要

为直观地反映环形交叉口内车辆的运行状态,建立了一种基于车道选择特性的环形交叉口车辆行程时间预测模型。利用车辆换道初始位置的临界累积概率标定了环形交叉口入环区、绕环区、出环区分界线;根据实地数据分析并建立了车辆的车道选择概率与流量的关系模型;综合考虑环岛的几何条件、车辆排队以及换道等因素的影响,建立了包含入环时间、绕环时间与出环时间的环形交叉口车辆行程时间预测模型。最后,通过实测数据对模型中参数进行标定。结果表明:本文模型的平均预测误差在10%以内,满足精度要求。该模型可为环形交叉口状态评价与控制方法提供依据。

关键词: 交通运输系统工程; 环形交叉口; 行程时间; 车道选择概率; 排队延误

中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2017)05-1411-09

Roundabout travel time prediction based on characteristics of lane choosing

LI Zhi-hui, WANG Kun-wei, SONG Xian-min, LIU Xin-shan, SHEN Yao, LUO Rui-qi

College of Transportation, Jilin University, Changchun 130022, China

Abstract

In order to directly reflect the traffic state at the roundabout, a model of vehicle travel time at roundabout was proposed based on vehicle lane choosing characteristics. The boundaries among the entering area, circling area and existing area at a roundabout are calibrated using the accumulative probability of the initial location of lane-changing. A relation model between the probability of lane choosing and traffic volume is developed with real field data. Considering the influences of the factors of roundabout geometry condition, vehicle queuing and lane changing, a travel time prediction model was established to obtain entering time, circling time and existing time. Finally, the model parameters were calibrated using survey data. Results show that the error of the prediction model is within 10% that meets the accuracy requirement. Thus, the model is beneficial for the traffic state evaluation and control method of the roundabout.

Key words: engineering of communication and transportation system; roundabout; travel time; probability of lane choosing; queuing delay

Show Figures

0 引言

环形交叉口作为一种特殊形式的平面交叉口, 在城市路网中发挥着重要作用。但随着车流量的增加, 环岛内出现了交通阻滞现象, 为了更好地发挥环岛的自组织特性, 需要根据环岛内车辆的运行状态对其采取恰当的控制方式, 而车辆在环岛内的行程时间能够反映出环岛内的运行状态, 因此, 对于环形交叉口车辆行程时间预测具有重要的意义。

目前, 对于行程时间的预测, 多是基于城市道路, 却鲜有关于环形交叉口内车辆行程时间的预测方面的研究内容。由于环形交叉口车辆换道以及排队会产生延误, 因此, 对于环形交叉口内车辆延误时间的计算是确定车辆在环形交叉口行程时间的关键。环形交叉口内车辆延误时间以及行程时间的计算方法可以分为理论研究、经验法和计算机建模。Troutbeck等^[1]提出了基于有限优先的间隙接受理论, 改进了环形交叉口的延误模型; 邱荣华等^[2]利用排队论分析环形交叉口的交通流特性, 并建立了环形交叉口车辆延误模型。在理论研究的基础上, 一些专家学者利用经验法以及计算机仿真对延误模型进行了研究。Chandra^[3]、Serhan^[4]等根据数据调查分析, 建立了环形交叉口的车辆延误与流量的关系模型; Bugg等^[5]分析了环形交叉口对干线速度影响区域, 从而建立了含有环形交叉口的干线车辆行程时间预测模型; 美国《道路通行能力手册》(HCM)^[6]通过采集美国各个环形交叉口的延误数据进行分析, 采用类似于无信号控制交叉口的方法进行交叉口车辆延误估计; 杨晓光等^[7]提出了基于HCM的改进环形交叉口车均延误模型; 丁柏群等^[8]用解析法建立了环形交叉口进口道内侧与外侧车道车辆延误及排队长度模型; 宋现敏等^[9]根据环岛内车流状态建立了车辆行程时间计算模型; 王震远^[10]采用VISSIM仿真, 对环形交叉口的车辆排队延误进行分析, 得到了车辆排队与延误之间的关系模型。上述研究大多从宏观的角度建立了环形交叉口的延误模型, 却没有考虑环岛内不同区域车辆车道选择特性不同对延误时间和行程时间产生的影响。由于车辆的车道选择产生的延误时间不可忽略, 因此对于环岛内车道选择特性的研究十分重要。国内外不少专家学者对车辆的车道选择特性进行了研究。王晓原等^[11]、耿现彩^[12]结合数理统计和仿真方法, 建立了流量与车辆车道选择的关系模型; Jin^[13]引入了车道变换强度的概念, 并建立了流量与车道变换强度的模型。Guido等^[14]分析了车辆的换道率与车头时距的关系, 提出了换道率与车头时距以及相邻车道后车速度的关系模型。综上所述, 国内外学者分别对环形交叉口的延误时间、换道率进行了研究, 这些研究成果对环形交叉口运行状态和行程时间估算有一定帮助。但对于多支路多环道的大型复杂环形交叉口, 进道口车流在不同的环道流量下, 车辆的车道选择特性存在较大的差异, 车辆的换道行为频繁, 因此, 研究基于车道选择特性的环形交叉口行程时间具有重要的现实意义。

本文首先根据车流运行轨迹, 将环形交叉口划分为入环区、绕环区、出环区3个区域; 分析了3个区域内车流的车道选择行为, 构建了车道选择概率与流量的关系模型; 结合环岛车流运行特性及几何条件, 分别建立了车辆在入环区、绕环区、出环区的行程时间, 从而构建了考虑车道选择特性的环形交叉口车辆行程时间预测模型; 最后, 利用长春市景阳广场实测数据对本文提出的模型进行了验证。

1 车道选择特性分析

1.1 区域划分

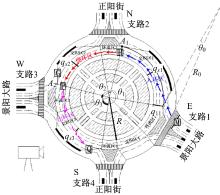
车辆在环形交叉口内的运行是一个复杂的过程, 对于固定路径的车辆, 由于受到环岛内复杂因素的影响, 使得车辆在环道内的车道选择特性不同, 导致车辆在环岛内的行驶轨迹也不同。其中, 固定路径的车辆是指从同一支路驶入并从另一个相同支路驶出环形交叉口的车辆, 其运行轨迹包含入环、绕环、出环3个部分。车辆在入环过程中, 根据环道内的可插车间隙进入相应的环道; 车辆在绕环过程中由于受到目标出口以及下游入环车辆的双重因素影响, 会根据环道内的情况进行车道选择; 车辆在出环的过程中受到目标出口的吸引, 选择相应的车道驶离环岛。因此, 本文根据车辆运动行为, 将固定路径车辆的空间运行轨迹划分为:入环区、绕环区、出环区3个区域。对于固定路径的车辆, 入环区是指从车辆所在进口道停车线至其进入环岛后经过的第一个交织区环流区分界线之间的区域; 绕环区是指入环区上界线至车辆在驶离环岛前经过的最后一个交织区环流区分界线之间的区域; 出环区是指绕环区上界线至车辆驶离环岛经过的最后一个交织区边界线之间的区域。图1是从东景阳大路驶入, 南正阳街驶出的车流轨迹, M至H为入环区、H至P为绕环区、P至Q为出环区。当绕环区内有n个交织区时, 称绕环区有n个绕环子区, 每个子区均包含一个环流区和一个交织区。

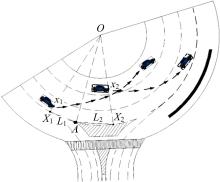
	Figure Option View Download New Window
	图1 固定路径车流区域划分图Fig.1 Area division for fixed path traffic

本文对入环区、绕环区、出环区的边界进行了标定, 车辆车道选择起始位置标定方法如下:出口隔离岛外侧点A为标定基准点, 车辆换道起始点标记为x, 其在最外侧环道上的投影点记作X, 车辆换道起点X与基准点A的矢量距离记作L(即|L|=AX), L定义为车辆换道起点相对位置。图2为车辆换道相对位置标定示意图。车辆换道起点为x₁, x₁在外侧环道上的投影点为X₁, 则车辆的换道位置为L₁, 由于点X₁在基准点A的左侧, 故L₁=-|AX₁|< 0。同理可知, L₂=AX₂> 0。

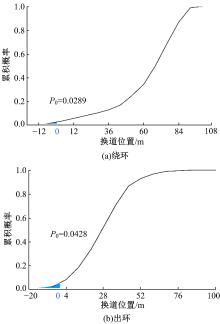
	Figure Option View Download New Window
	图2 车辆换道起始位置标定示意图Fig.2 Schematic diagram of calibrate initial location of lane changing

采用上述车辆车道选择起始位置标定方法, 分别以图1中景阳广场北出口隔离岛外侧点A₁、西出口隔离岛外侧点A₂为基准点对固定路径绕环和出环车辆的换道起始位置进行标定, 得到环道内车辆换道起始位置与其累积概率的关系如图3所示。其中, 横坐标0分别为A₁、A₂点所在位置, 横坐标其余值为车辆换道起始位置在外侧环道上投影点距离A₁、A₂的矢量距离。

从图3可以看出, 对于该固定路径的车流在进入绕环区和出环区之前进行车道选择的累积概率均小于5%。因此, 本文中将入口到相邻的交织区上界线作为入环区和绕环区的分界线, 将出口上游环流区下界限作为绕环区和出环区的分界线。

	Figure Option View Download New Window
	图3 环道内车辆换道位置累积分布曲线Fig.3 Cumulative distribution curve of lane changing

1.2 入环区的车道选择特性

对于单环道的环形交叉口, 进口道车辆在进入环道的过程中, 需要等待一个可插车间隙完成入环行为; 而对于多环道的环形交叉口, 进口道车辆根据各环道提供的间隙经过多次换道和跟随行驶完成最终的入环行为。通过实地调查发现, 在多环道的环形交叉口内入环车辆选择进入各环道的概率和与其冲突的环道流量有关。环道流量较大时, 入环车辆进入内侧环道的难度加大, 多数车辆会选择外侧车道行驶。其中, 内侧环道是指距离中心岛最近的环道(文中称环道1, 其余的环道依次为环道2、环道3、…、环道k), 外侧环道是指最右侧的环道。利用三环道的长春市景阳广场实测数据, 统计得到入环车辆选择各个环道行驶的概率, 并将统计得到的185组数据按流量等间隔分为27组, 组间隔为60, 求得组内均值, 结果如表1所示。

表1 环道流量与入环车辆选择环道的概率统计 Table 1 Probability statistics of traffic flow and selection of circulatary roadway for the entry flow

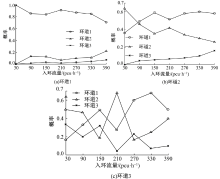
	Figure Option View Download New Window
	图4 不同环道流量下入环车辆的环道选择特性Fig.4 Lane choosing characteristics of entering vehicles under different traffic flow

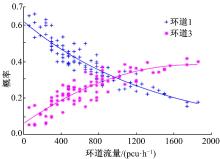
对统计得到的固定路径下入环车辆进入各环道的概率和环道流量进行分析, 可知入环车辆选择环道1、环道3行驶的概率与环道流量之间存在显著的相关关系,

双侧显著性指标分别为α ₁=0.0070, α ₃=0.0012, 入环车辆选择环道2行驶的概率与环道流量之间的双侧显著性指标为α ₂=0.2748, 关系并不显著。图4为车辆选择环道1和环道3的概率与环道流量的关系。对统计得到的数据进行分析, 发现入环车辆选择内侧环道的概率与环道流量的关系为指数形式, 入环车辆选择外侧环道的概率与环道流量的关系为二次函数形式, 本文建立了入环车辆的车道选择概率与环道流量的关系模型, 表达式为:

$\begin{matrix} \begin{matrix} P_{1} = a_{1} e^{b_{1} q_{11}} (1) \\ P_{3} = a_{3} q_{11}^{2} + b_{3} q_{11} + c (2) \end{matrix} \end{matrix}$

式中:a₁、a₃、b₁、b₃、c均为待定系数; P₁、P₃分别为入环车辆选择环道1、环道3行驶的概率; q₁₁为环道总流量, pcu/h。

入环车辆进入环道2的概率为:

$\begin{matrix} P_{2} = 1 - P_{1} - P_{3} (3) \end{matrix}$

1.3 绕环区的车道选择特性

王晓原等^[11]发现, 车辆的车道选择与所在时段流量有直接关系。韩萍^[15]等通过统计分析方法研究了环形交叉口的流量因素与车辆换道率的关系, 并建立了统计回归模型。段宇洲^[16]根据调查数据定性的说明了环道内车辆车道选择与流量的关系。对于固定路径的车辆, 进入绕环区之后为了能够尽快通过离开环岛, 就需要根据绕环区的状态进行车道选择。分别对长春市景阳广场各绕环区不同环道车辆的换道概率与入环流量的关系进行统计, 如图5所示。

通过对图5绕环区车辆的车道选择分析, 得到不同入环流量下环道车辆的车道选择标准偏差最大为32.64%, 最小为4.11%, 平均标准偏差为13.74%, 因此图5中得到的换道概率可以表示在不同进口道流量下的车道选择情况, 即不同时段、不同入环流量下各环道的车道选择概率P_id不同。

	Figure Option View Download New Window
	图5 绕环区各环道车辆的车道选择特性分析Fig.5 Analysis of lane choosing in circle area

2 环形交叉口行程时间建模

根据车流在环岛内的空间运行轨迹, 车辆在环岛内的运行区域包括入环区、绕环区、出环区3个部分, 称车辆在上述3个部分内的运行时间分别为入环时间、绕环时间、出环时间。车辆在环形交叉口内的运行时间与上述三者之间的关系如下:

$\begin{matrix} T = t_{1} + \overset{m}{\sum_{n = 0}} t_{2 n} + t_{3} \end{matrix}$ (4)

式中:t₁为入环时间, s; m为固定OD车流所经过的绕环子区总数; t₂_n为车流经过第n个绕环子区的时间, s, n=0, 1, …, m; t₃为出环时间, s。

2.1 入环时间

当环道内流量较小时, 车辆以自由流速度通过入环区; 当环道流量增大时, 车辆需要选择合适的可插车间隙进入环道行驶, 由此产生了入环车辆选择环道延误时间以及排队延误时间。因此, 将环形交叉口内车辆的入环时间分为畅行行驶时间t₁₁、入环车辆选择环道延误时间t₁₂和入环车辆的排队延误时间t₁₃。车辆的入环时间为上述三者之和。

2.1.1 畅行时间

畅行行驶时间是指环形交叉口内的车辆以自由流的状态行驶所用的时间, 即车辆间无相互干扰时, 车辆的行驶时间由行驶距离和行驶速度决定。畅行行驶时间模型如下:

$\begin{matrix} t_{0} = \frac{L}{v} \end{matrix}$ （5）

式中:L为车辆行驶距离, m; v为车辆在无干扰的情况下的行驶速度, m/s。

2.1.2 延误时间

(1)入环选择环道延误时间

入环车辆选择不同的环道时, 由于冲突车辆数不同, 导致入环车辆进入不同环道的换道延误时间不同。本文引用Chandra等^[3]提出的冲突车辆数与平均延误时间经验模型:

$\begin{matrix} t_{12 i} = w_{1 i} {q_{ci}}^{k_{1 i}} = w_{1 i} (\overset{i}{\sum_{j = k - i + 1}} q_{11 j})^{k_{1 i}} \end{matrix}$ （6）

式中:w₁_i、k₁_i为待定系数; k为环道车道总数; q_c_i为与进入环道i的入环车辆冲突的环道车辆数, pcu/h; q₁₁_j为与入环车流冲突的环道j的车辆数, pcu/h。

入环车流受到环道车流的影响, 进入各个环道的车流比例以及进入各个环道的延误时间不同。因此, 入环车辆选择环道延误平均时间为:

t₁₂= $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ P_it₁₂_i= $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ P_iw₁_i( $\begin{matrix} \overset{i}{\sum_{j = k - i + 1}} \end{matrix}$ q₁₁_j $\begin{matrix} )^{k_{1 i}} \end{matrix}$ (7)

式中:P_i为入环车流进入环道i的概率。

(2)排队延误时间

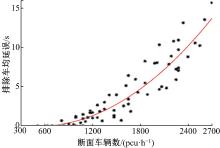
由于环形交叉口流量增大到一定程度时, 车辆的排队延误时间与环道断面的流量有关。通过统计长春市景阳广场入口车辆排队和入口停车线断面流量以及环道车辆排队延误和交织区中间断面流量, 可得环形交叉口内车辆的排队延误和相应的断面流量之间的关系, 如图6所示。当断面车流量q_s> q_e(q_e为一定值)时, 曲线与二次曲线相似, 且R²≥ 85%。则排队车均延误时间t_q可以表示为:

$\begin{matrix} t_{q} = \{\begin{matrix} 0, q_{s} \leq q_{e} \\ β q_{s}^{2} + δ q_{s} + γ, q_{s} > q_{e} \end{matrix} \end{matrix}$ （8）

式中:β 、δ 、γ 均为待定系数。

	Figure Option View Download New Window
	图6 排队车均延误与断面车辆数关系图Fig.6 Relationship between average delay and number of vehicles in cross section

将式(5)(7)(8)三者相加, 得到车辆的入环时间表达式:

$\begin{matrix} \begin{matrix} t_{1} = \frac{L_{1}}{v} + \overset{k}{\sum_{i = 1}} P_{i} w_{1 i} (\overset{k}{\sum_{j = k - i + 1}} q_{11 j})^{k_{1 i}} + t_{q 1} = \\ \{\begin{matrix} \frac{θ_{0} R_{0} + θ_{1} R}{v} + \overset{k}{\sum_{i = 1}} P_{i} w_{1 i} (\overset{k}{\sum_{j = k - i + 1}} q_{11 j})^{k_{1 i}}, \\ q_{s 1} \leq q_{e 1} \\ \frac{θ_{0} R_{0} + θ_{1} R}{v} + \overset{k}{\sum_{i = 1}} P_{i} w_{1 i} (\overset{k}{\sum_{j = k - i + 1}} q_{11 j})^{k_{1 i}} + \\ β_{1} q_{s 1}^{2} + δ_{1} q_{s 1} + γ_{1}, q_{s 1} > q_{e 1} \end{matrix} \end{matrix} \end{matrix}$ （8）

式中:L₁为车辆在入环区行驶距离, m; t_q1为入环车流平均排队延误时间, s; θ ₀为进口道停车线与交织区进口道入口之间的角度, rad; R₀为车辆在进口道停车线与交织区进口道间车辆的轨迹半径, m; θ ₁为入环区边界(见图1)的夹角, rad; R为环岛半径加上所有环道宽度的1/2, m; β ₁、δ ₁、γ ₁均为待定系数; q_s1为入口断面流量, pcu/h; q_e1为临界流量, pcu/h。

2.2 绕环时间

驾驶员在绕环区行驶的过程中同样受到环岛的几何条件、环道流量以及入环流量等因素的影响。即绕环时间包括车辆在绕环区的畅行时间, 绕环车辆换道产生的延误时间以及绕环车辆的排队延误时间。其中畅行行驶时间和排队延误时间分别可以根据式(5)和式(9)求得。因此, 只需建立车辆的换道延误时间模型。

车辆在绕环区和出环区行驶时, 要根据环岛内的条件以及自身需求进行相应的换道行为。定义车辆由环道i进入环道d(当车辆出环时, d=k)的过程车辆进行了μ (μ =|d-i|)次换道, 相应的延误时间为t_μ。不同次数的换道延误时间如下:

$\begin{matrix} \{\begin{matrix} t_{μ} = 0, μ = 0 \\ t_{μ} = t'_{21}, μ = 1 \\ ⋮ \\ t_{μ} = t'_{2 (d - i)}, μ = | d - i | \end{matrix} \end{matrix}$ （10）

式中:t'₂₁、t'₂₍_d-i₎分别为绕环区车辆进行一次换道、d-i次换道的平均延误时间, s。

绕环车辆的换道平均延误时间为:

$\begin{matrix} t_{22} = \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id}, i = d \pm μ \end{matrix}$ （11）

结合式(2)(7)(9)可以得到绕环时间模型如下:

$\begin{matrix} \begin{matrix} t_{2} = \frac{L_{2}}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id} + t_{q 2} = \\ \{\begin{matrix} \frac{θ_{2} R}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id}, q_{s 2} \leq q_{e 2} \\ \frac{θ_{2} R}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id} + β_{2} {q_{s 2}}^{2} + δ_{2} q_{s 2} + γ_{2}, \\ q_{s 2} > q_{e 2} \end{matrix} \end{matrix} \end{matrix}$ （12）

式中:L₂为车辆在绕环区行驶距离, m; t_q2为绕环车流平均排队延误时间, s; θ ₂为绕环区边界(见图1)的夹角, rad; q_s2为绕环区断面流量pcu/h; β ₂、δ ₂、γ ₂均为未知参数; q_e2为临界流量, pcu/h。

2.3 出环时间

出环区车辆的出环时间影响因素与绕环区车辆行程时间影响因素相同, 因此, 得到出环时间模型如下:

$\begin{matrix} \begin{matrix} t_{3} = \frac{L_{3}}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id} + t_{q 3} = \\ \{\begin{matrix} \frac{θ_{3} R}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id}, q_{s 3} \leq q_{e 3} \\ \frac{θ_{3} R}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id} + β_{3} {q_{s 3}}^{2} + δ_{3} q_{s 3} + γ_{3}, \\ q_{s 3} > q_{e 3} \end{matrix} \end{matrix} \end{matrix}$ （13）

式中:L₃为车辆在绕环区行驶距离, m; t_q3为绕环车流平均排队延误时间, s; θ ₃为绕环区边界(见图1)的夹角, rad; q_s3为绕环区断面流量, pcu/h; β ₃、δ ₃、γ ₃均为未知参数; q_e3为临界流量, pcu/h。。

车辆在环形交叉口内的行程时间与其在环形交叉口内的运行轨迹直接相关。结合式(9)(12)(13)可以得到当车辆通过支路数为N的环形交叉口时, 经过m(m=0, 1, …, N-3)个绕环子区的行驶时间计算模型如下:

$\begin{matrix} \begin{matrix} T = t_{1} + \overset{m}{\sum_{n = 0}} t_{2 n} + t_{3} = \\ \frac{L_{1}}{v} + \overset{k}{\sum_{i = 1}} P_{i} w_{1 i} (\overset{k}{\sum_{j = k - i + 1}} q_{11 j})^{k_{1 i}} + t_{q 1} + \\ \overset{m}{\sum_{j = 1}} (\frac{L_{2 j}}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μj} \sum P_{i} P_{id} P_{d h} \dots P_{sk} + t_{q 2 j}) + \\ \frac{L_{3}}{v} + \overset{d - 1}{\sum_{μ = 1}} t_{μ} \overset{k}{\sum_{d = 1}} P_{i} P_{id} + t_{q 3} \end{matrix} \end{matrix}$ （14）

式中:L₂_j为车辆在绕环子区j的行驶距离, m; t_{μ j}为车辆在绕环子区j的换道平均延误时间, s; ∑ P_iP_idP_dh…P_sk为车辆从进口道进入环道, 在m个绕环子区内经过多次换道, 最终在第m个绕环子区的k车道上行驶这一事件的发生概率; t_q2_j为车辆在绕环子区j的排队平均延误时间产, s。

3 模型验证

3.1 数据获取

以长春市景阳广场为例, 其几何条件如图1所示。通过对采集到的视频数据利用Matlab软件编程处理得到时间间隔为0.02 s的图片, 并结合人工数据采集的方式获取相关数据。由于本文主要针对景阳广场从支路1入环车辆进行研究, 采集的数据包括以下6个部分:①车辆经过图1中各个断面(断面M、H、G、P、Q)的时刻。②各时段入环车辆在入环区(图1中断面M与断面H之间的区域)的环道选择情况。③各时段从支路4出环车辆在绕环区(图1中断面H与断面P之间的区域)的车道选择情况。④各时段从支路3出环车辆在出环区(图1中断面H与断面G之间的区域)的车道选择情况。⑤各时段从支路4出环车辆在出环区(图1中断面P与断面Q之间的

区域)的车道选择情况。⑥每分钟通过进口道2和进口道3以及环岛各断面的车辆数。

通过对数据①的处理, 得到从环道1进入的车辆通过环形交叉口各区域以及通过整个环形交叉口的行程时间; 通过处理数据②③④⑤⑥, 得到车辆在环岛各区域的车道选择情况和环岛各断面的流量。

3.2 参数标定

首先对模型中的参数进行标定, 调查时间为上午8:00~9:30, 下午4:30~6:00, 取其中80%的数据进行参数标定。通过调查得到景阳广场的几何参数, 如表2所示。

表2 景阳广场几何参数表 Table 2 Geometric parameters of Jingyang square

利用采集的从支路1入环, 支路3出环以及支路4出环的入环区和出环区车流的相应断面流量和车辆车道选择情况, 对入环时间t₁和出环时间t₃中参数分别进行标定。并结合支路1入环、支路4出环车流在绕环区相应的调查数据, 对绕环时间t₂中的未知参数进行标定。最终得到入环时间t₁、绕环时间t₂和出环时间t₃中参数标定结果, 如表3所示。

表3 参数标定结果 Table 3 Results of parameter calibration

3.3 结果分析

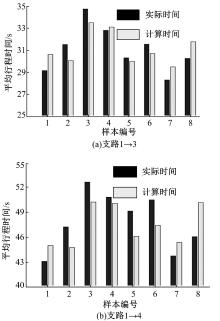
利用上文中标定得到的各个参数, 取剩下的20%的数据利用模型进行验证, 分别计算得到支路1至支路3和支路1至支路4的车流行程时间, 与实际调查数据对比, 分析结果如图7所示, 其中, 图7中各图均是将剩下的32组数据平均分成8组, 即每一个样本值是4 min内入环车辆行程时间平均值。

	Figure Option View Download New Window
	图7 实际行程时间与计算时间对比Fig.7 Comparison between actual value and calculated value of travel time

由公式计算得到从支路1入环且从支路3出环车辆行程时间的计算值与实际调查的行程时间最大相对误差为12.61%, 最小相对误差为0.95%, 平均相对误差为7.71%。从支路1入环且从支路4出环车辆行程时间的计算值与实际调查的行程时间最大相对误差为15.82%, 最小相对误差为0.49%, 平均相对误差为6.91%。由于本文预测模型得到的预测结果的平均误差均小于10%, 在可接受的范围内, 因此, 该模型对于环形交叉口车辆行程时间的预测具有一定的可靠性。

4 结束语

结合车辆换道起始位置的临界累积概率标定了环形交叉口入环区、绕环区、出环区分界线, 明确地将固定路径车流轨迹进行了区域划分。利用长春市景阳广场调查数据分析了各个区域的车道选择特性, 并基于此建立了车辆的车道选择概率与流量的关系模型。综合考虑环形交叉口内的几何条件、车道选择以及排队延误等因素, 建立了入环时间模型、绕环时间模型、出环时间模型, 从而构建了固定路径下环形交叉口车辆行程时间预测模型。最后, 采用长春市景阳广场的视频检测数据, 对模型中参数进行了标定, 并代入数据进行模型验证, 结果表明:本文模型的平均预测误差在10%以内, 满足精度要求。本文所建立的环形交叉口车辆行程时间预测模型能够很好地反映车辆在环形交叉口内的运行状态, 并能够为环形交叉口控制方法的选取提供依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Troutbeck R J, Kako S. Limited priority merge at unsignalized intersections[J]. Transportation Research Part A: Policy & Practice, 1997, 33(3/4): 291-304. [本文引用:1]
[2]	邱荣华, 李文权. 低渠化环形交叉口延误理论模型研究[J]. 交通运输工程与信息学报, 2005, 3(1): 104-107. Qiu Rong-hua, Li Wen-quan. Study of the delay theory model for low channeling roundabouts[J]. Journal of Transportation Engineering and Information, 2005, 3(1): 104-107. [本文引用:1]
[3]	Chand ra S, Agrawal A, Rajamma A. Microscopic analysis of service delay at uncontrolled intersections in mixed traffic conditions[J]. Journal of Transportation Engineering, 2009, 135(6): 323-329. [本文引用:2]
[4]	Serhan T, Kübraç, Mustafaö, et al. Different approaches to minimum delay prediction at single-lane traffic circles in Izmir, Turkey[J]. Canadian Journal of Civil Engineering, 2013, 40(3): 274-284. [本文引用:1]
[5]	Bugg Z, Schroeder B J, Jenior P, et al. Methodology to compute travel time of a roundabout corridor[J]. Journal of the Transportation Research Board, 2015 (2483): 20-29. [本文引用:1]
[6]	Highway Capacity Manual2010[ Z]. [本文引用:1]
[7]	杨晓光, 赵靖, 汪涛. 环形交叉口信号控制最佳周期计算方法[J]. 中国公路学报, 2008, 21(6): 90-95. Yang Xiao-guang, Zhao Jing, Wang Tao. Optimal cycle calculation method of signal control at roundabout[J]. China Journal of Highway and Transport, 2008, 21(6): 90-95. [本文引用:1]
[8]	丁柏群, 裴煦. 环形信号交叉口进口道车辆延误及排队长度计算方法[J]. 交通信息与安全, 2015, 33(3): 47-52. Ding Bo-qun, Pei Xi. Calculating methods for vehicle delay and queue length at signalized roundabouts[J]. Computer and Communications, 2015, 33(3): 47-52. [本文引用:1]
[9]	宋现敏, 刘焕峰, 李志慧, 等. 基于OD分布的环形交叉口车辆行程时间建模[J]. 吉林大学学报: 工学版, 2016, 46(1): 70-75. Song Xian-min, Liu Huan-feng, Li Zhi-hui, et al. New model of vehicle travel time at roundabout based on OD distribution[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(1): 70-75. [本文引用:1]
[10]	王震远. 城市道路环形交叉口车辆排队及行车延误研究[J]. 北京建筑工程学院学报, 2004, 20(3): 54-58. Wang Zhen-yuan. Study on queuing and traffic delay in the roundabout of urban road[J]. Journal of Beijing Institute of Civil Engineering and Architecture, 2004, 20(3): 54-58. [本文引用:1]
[11]	王晓原, 徐峰. 微观交通仿真研究不同流量条件下的车道利用率[J]. 曲阜师范大学学报: 自然科学版, 2004, 30(4): 15-19. Wang Xiao-yuan, Xu Feng. Study on the lane utilization ratio under different volumes with microscopic traffic simulation[J]. Journal of Qufu Normal University (Natural Science), 2004, 30(4): 15-19. [本文引用:2]
[12]	耿现彩. 环形交叉口车道选择行为对其性能的影响研究[C]//2015年中国城市交通规划年会暨第28次学术研讨会, 杭州, 2015. [本文引用:1]
[13]	Jin W L. A kinematic wave theory of lane-changing traffic flow[J]. Transportation Research Part B Methodological, 2010, 44(8/9): 1001-1021. [本文引用:1]
[14]	Guido G, Vitale A. A Behavioral lane changing model for roundabout design[J]. WIT Transactions on the Built Environment, 2005, 82: 567-576. [本文引用:1]
[15]	韩萍. 环形交叉口交通流运行特性[D]. 长春: 吉林大学交通学院, 2011. Han Ping. Traffic operation characteristics of roundabout[D]. Changchun: College of Transportation, Jilin University, 2011. [本文引用:1]
[16]	段宇洲. 环形交叉口交通流运行特性及控制方法研究[D]. 长春: 吉林大学交通学院, 2015. Duan Yu-zhou. Traffic flow operational characteristics and control methods at roundabouts[D]. Changchun: College of Transportation, Jilin University, 2015. [本文引用:1]

1997

0.0

... Troutbeck等^[1]提出了基于有限优先的间隙接受理论,改进了环形交叉口的延误模型 ...

2005

0.0

. 2005, 3(1):104-107 DOI:doi:10.3969/j.issn.1672-4747.2005.01.020

Study of the delay theory model for low channeling roundabouts

低渠化环形交叉口延误理论模型研究

Qiu Rong-hua , Li Wen-quan.

邱荣华, 李文权

研究环形交叉口的延误,用排队论方法分析低渠化环形交叉口的交通流特性,提出环形交叉口通行能力、延误研究的基本思路,建立单向两进口车道与两环行车道的环形交叉口车流延误模型,得出环形交叉口进口道车流延误时间与自由流比例有关;与行车最小车头时距有关;与环形交叉口通行能力有关;与交叉口车流交织段长度有关.模型对环形交叉口的规划、设计以及服务水平的评价具有指导意义.

... 邱荣华等^[2]利用排队论分析环形交叉口的交通流特性,并建立了环形交叉口车辆延误模型 ...

2009

0.0

... Chandra^[3]、Serhan^[4]等根据数据调查分析,建立了环形交叉口的车辆延误与流量的关系模型 ...

... 本文引用Chandra等^[3]提出的冲突车辆数与平均延误时间经验模型: ...

2013

0.0

... Chandra^[3]、Serhan^[4]等根据数据调查分析,建立了环形交叉口的车辆延误与流量的关系模型 ...

2015

0.0

... Bugg等^[5]分析了环形交叉口对干线速度影响区域,从而建立了含有环形交叉口的干线车辆行程时间预测模型 ...

2010

0.0

... 美国《道路通行能力手册》(HCM)^[6]通过采集美国各个环形交叉口的延误数据进行分析,采用类似于无信号控制交叉口的方法进行交叉口车辆延误估计 ...

2008

0.0

. 2008, 21(6):90-95

Optimal cycle calculation method of signal control at roundabout

环形交叉口信号控制最佳周期计算方法

Yang Xiao-guang , Zhao Jing , Wang Tao.

杨晓光, 赵靖, 汪涛

针对信号控制环形交叉口这一特殊的控制对象,运用理论解析结合计算机仿真检验的方法,分别给出环形交叉口直行和左转的延误计算模型;并在此基础上提出了一种以交叉口车均延误最小为目标,适合于在非饱和状态下采用多进口道放行协同环道控制环形交叉口的最佳周期值计算方法。最后通过模拟试验和实例分析对模型的适用性进行了检验。结果表明:该模型有较高的精度和可靠性,为求解环形交叉口信号控制最佳周期提供了一种有效的新算法。

... 杨晓光等^[7]提出了基于HCM的改进环形交叉口车均延误模型 ...

2015

0.0

. 2015, 33(3):47-52 DOI:doi:10.3963/j.issn.1674-4861.2015.03.008

Calculating methods for vehicle delay and queue length at signalized roundabouts

环形信号交叉口进口道车辆延误及排队长度计算方法

Ding Bo-qun , Pei Xi.

丁柏群, 裴煦

摘　要：由于环形交叉口的内在局限性,大部分的环形交叉口被改造为常规的十字交叉口或环形信号交叉口.为了分析环形交叉口内车流特性,针对环形信号控制交叉口,分析影响进口车道车辆延误与排队长度的因素;提出了2种常见的环形交叉口相位方案;根据每种相位方案,考虑进口道内侧车道、外侧车道的交通流运行特性,分别建立了进口道内侧车道、外侧车道的车均延误和平均排队长度计算模型,将内外侧车道区别考虑有利于分析环形交叉口内车流特性.以哈尔滨市博物馆环形交叉口为例,通过Vissim 仿真软件得到仿真结果,将模型计算结果与仿真输出结果进行比较,结果基本相近.论证了模型的准确性.

... 丁柏群等^[8]用解析法建立了环形交叉口进口道内侧与外侧车道车辆延误及排队长度模型 ...

2016

0.0

. 2016, 46(1):70-75

New model of vehicle travel time at roundabout based on OD distribution

基于OD分布的环形交叉口车辆行程时间建模

Song Xian-min , Liu Huan-feng , Li Zhi-hui

宋现敏, 刘焕峰, 李志慧

... 宋现敏等^[9]根据环岛内车流状态建立了车辆行程时间计算模型 ...

2004

0.0

. 2004, 20(3):54-58 DOI:doi:10.3969/j.issn.1004-6011.2004.03.014

Study on queuing and traffic delay in the roundabout of urban road

城市道路环形交叉口车辆排队及行车延误研究

Wang Zhen-yuan.

王震远

随着国民经济的快速发展 ,城市机动车保有量持续增加 ,由此引起了一系列的交通问题 .结合北京市东四十条桥环形交叉口的交通状况 ,采用VISSIM交通微观仿真系统 ,对环形交叉口车辆排队及行车延误进行了分析研究 ,得出了车辆排队及延误与通行能力影响因素之间的关系

... 王震远^[10]采用VISSIM仿真,对环形交叉口的车辆排队延误进行分析,得到了车辆排队与延误之间的关系模型 ...

2004

0.0

. 2004, 30(4):15-19

Study on the lane utilization ratio under different volumes with microscopic traffic simulation

微观交通仿真研究不同流量条件下的车道利用率

Wang Xiao-yuan , Xu Feng.

王晓原, 徐峰

... 王晓原等^[11]、耿现彩^[12]结合数理统计和仿真方法,建立了流量与车辆车道选择的关系模型 ...

... 3 绕环区的车道选择特性王晓原等^[11]发现,车辆的车道选择与所在时段流量有直接关系 ...

2015

0.0

. 2015, :-

环形交叉口车道选择行为对其性能的影响研究

耿现彩

环形交叉是道路平面交叉的一种常见形式,也是城市道路网络的重要节点。为了研究环形交叉口的车道选择行为对交叉口性能的影响,选取典型环形交叉口,从制高点拍摄现场影像,利用数学统计分析方法,得到错误的车道选择行为在我国具有普遍性的结论,并利用微观仿真软件实验得到,随着交叉口错误的车道选择行为比例增加,交叉口性能评价指标值逐渐增加,交叉口性能渐趋恶化。因此,有效引导驾驶员的车道选择行为是减少环形交叉口的交通冲突、规范环形交叉口的车辆运行秩序、有效避免交通事故的可行措施。

... 王晓原等^[11]、耿现彩^[12]结合数理统计和仿真方法,建立了流量与车辆车道选择的关系模型 ...

2010

0.0

... Jin^[13]引入了车道变换强度的概念,并建立了流量与车道变换强度的模型 ...

2005

0.0

... Guido等^[14]分析了车辆的换道率与车头时距的关系,提出了换道率与车头时距以及相邻车道后车速度的关系模型 ...

2011

0.0

. 2011, :-

Traffic operation characteristics of roundabout[D]. Changchun:College of Transportation,

环形交叉口交通流运行特性[D]

Han Ping.

韩萍

本论文主要是依托国家自然科学基金重点项目“城市路网动态交通管理与控制关键理论及其模拟技术研究”及辽宁省教育厅项目“环形交叉口通行能力与交通组织研究”,对环形交叉口交通流运行特性进行了深入研究。环形交叉口是在几条相交道路的平面交叉口中央设置一个半径较大的中心岛,使所有经过交叉口的直行和左转车辆都绕着中心岛作逆时针方向行驶,在其行驶过程中将车流的冲突点变为交织点,从而保证交叉口的行车安全,提高交叉口的通行能力。对环形交叉口交通流运行特性的实测与分析具有重要的理论及实际意义,将为环形交叉口通行能力、延误及服务水平分析,交叉口渠化设计、交通组织等提供重要的理论基础。本文通过对大连市十余个环形交叉口长期交通调查,分析我国环形交叉口交通流运行的基本特性与规律,提出环形交叉口交通流分析的相关方法,为建立一套适合我国交通环境的环形交叉口分析、组织及设计方法提供依据。论文主要由如下三部分构成： 1)环形交叉口几何特性及车辆运行行为几何特性是环形交叉口的固有属性,直接决定了环形交叉口车辆的运行行为。本部分首先对环形交叉口的相关几何特性进行了归纳总结,对环形交叉口类型进行了分类,对环形交叉口区域做了详细划分,并对各区域车辆运行特性进行了深入分析。在此基础上,以车辆换道率作为主要研究对象,研究了环形交叉口车辆换道行为特性及其与交叉口流量、支路数、交织区长度等参数的关系,通过实测数据建立了定量关系模型,为后续对交通流特性的研究奠定了基础。 2)环形交叉口交通流特征参数对大连市区内主要环形交叉口进行了多尺度、长时间的交通数据实地调查,积累了大量环形交叉口交通流运行数据。通过分析支路车辆到达、驶离规律及交织区车辆到达特性,建立了车辆到达分布规律模型。从宏观角度分析了环形交叉口不同空间位置上流量波动特性,从微观角度研究了转弯半径、入口车道宽度、入口车道数、交织区长度、中心岛半径、外环半径以及环道车流量等参数对入口流量的影响,并建立了线形回归模型。通过对环形交叉口不同时空尺度下速度数据特征量的聚类分析,得到了在不同的环形交叉口内部,相同位置车道内车速分布规律趋于一致的结论,进而通过应用核密度估计法建立速度分布模型,得到速度分布规律特性。通过核密度速度分布模型,对各环形交叉口分车道车速分布规律进行比较分析,对不同位置车道、支路数、交叉口几何尺度对车速的影响进行了定性分析并通过应用方差分析方法,从定量的角度验证上述结论。通过对畅通与拥堵两种交通状态数据的分析,提出了应用混合分布模型描述环形交叉口复杂的交通流车头时距分布。假定自由状态下车头时距分布规律服从负指数分布,拥挤状态下车头时距服从对数正态分布,建立车头时距分布模型并应用EM算法确定模型参数取值。通过与指数分布、爱尔朗分布和M3分布模型进行对比,结果表明,针对情况复杂的实测数据,混合分布的拟合精度远高于其他分布模型。 3)环形交叉口交通流运行效率按照不同主路车流之间是否存在相互影响,分别采用一车道模式、叠加双车道模式和同步双车道模式进行处理,建立了同步多车道模式下的无效数据剔除规则,并基于极大似然估计提出了三种模式下多车道临界间隙的估计方法。通过分析支路车辆驾驶员在穿越主路车流的微观选择特性,以风险时间函数和等待时间函数为基础,提出了临界间隙与主路车流流量的函数关系模型,该模型从理论角度考虑了主路车流的运行状态对主路车流临界间隙的影响,能够更好的符合实际情况。以大连市的实际观测数据为基础,统计分析了临界间隙与等待时间的曲线回归模型,在此基础上,结合环形交叉口交通流运行效率影响因素的分析,提出了通行能力的一般表达模型,并对模型相关参数进行了标定。以排队理论为纽带,推导了车均延误与通行能力的关系模型,并利用五四广场和隆泉广场的实际数据,验证了模型具有较高的精度。最后,论文对所做工作进行了总结,分析了论文所取得的进展及成果,并提出了需要进一步研究的内容。

... 韩萍^[15]等通过统计分析方法研究了环形交叉口的流量因素与车辆换道率的关系,并建立了统计回归模型 ...

2015

0.0

... 段宇洲^[16]根据调查数据定性的说明了环道内车辆车道选择与流量的关系 ...