模型假设电动自行车行驶在机非隔离的电动自行车道路上, 并且在具有一定宽度的车道上行驶(车道宽度为1.3 m左右), 每条车道都是理想的平坦无障碍的道路, 不考虑驾驶员期望速度的差异性, 无其他类型的车辆混行, 当车辆满足换道条件时, 立即完成换道行为。

在元胞自动机模型中, 元胞参数的标定是仿真的基础。本文元胞长度为2 m, 元胞宽度为1.3 m, 最大速度为3 cell/s^[2]。其中元胞长度是考虑电动车车长加上安全距离所得, 元胞宽度是结合车辆宽度及最大速度下要求的侧向净宽, 同时根据实际观测的数据统计获得。这与已有研究以及国内相关调查基本一致^[1]。

模型的更新规则主要分为两个部分, 第一部分为前进规则模型, 引用单车道元胞自动机模型中的NaSch改进模型-速度效应模型(VE)^[4], 采用并行更新方式, 周期性边界条件; 第二部分为换道规则模型, 本文应用局部最大熵原理, 设计换道规则。提出换道方向为局部熵增方向, 并按一定的概率实施换道(熵增换道概率), 更新方式采用串行更新。

1.3.1 前进规则

以往对于多车道非机动车元胞自动机的仿真研究中, 大都是以NaSch模型(单车道机动车仿真模型)做为前进规则^[4], 另外设计换道规则; 而在单车道机动车元胞仿真研究中, 存在着对NaSch模型的诸多改进模型, 对于机动车交通流的仿真改进模型有更好的效果; 本文在诸多分析、尝试后, 发现速度效应模型(VE)^[4]同样能够更好的模拟电动自行车流, 因为电动自行车驾驶员也会考虑前车的速度来控制自己的车速, 为此使用速度效应模型作为本文模型的前进规则。

速度效应模型是在传统的NaSch模型的基础上考虑前车的速度, 修改减速步形成的, 规则如下^[4]:

Step1:加速, v_n→ min(v_n+1, v_max) (1)

Step2:减速, v_n→ min(v_n+1, d_n+v_max) (2)

v'max=minvmax-1, vn+1, max0, dn+1-1(3)

Step3:随机慢化, 以概率p, v_n→ min(v_n-1, 0) (4)

Step4:运动, v_n→ x_n+v_n (5)

这里, x_n、v_n分别表示n车的位置和速度, d_n=x_n+1-x_n-l_veh表示n车和前车n+1之间的空元胞数, l_veh表示车辆长度(在计算d_n时特指车辆n+1的长度), v'_n+1是n+1车在t→ t+1时间步里的虚拟速度。相关研究已经证实^[4], 该模型在确定性条件下能得到亚稳态和回滞现象。

1.3.2 换道规则

(1)换道波的形成和传播机理分析

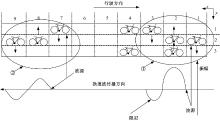
在非机动车交通流中, 前车的换道行为可能会也引发后方一系列车的换道, 即换道这种行为可以传播; 同时这种传播需要时间, 具有一定的传播速度, 并需要传播介质(若车辆后方长距离内无车, 这种影响将不能传递), 方向为从前向后单向传播, 为了描述的方便, 定义这种换道行为的传播为“ 换道波” 。若把车辆在平面道路的运动按照横向和纵向分解, 对于横向而言, 车辆的运动即为换道, 产生向后传播的换道波, 即质点的运动方向(横向)与波的传播方向(纵向)垂直, 故而换道波是横波; 对于纵向而言, 车辆向前加减速行驶, 引发道路上车辆疏密的传播即为传统交通波(如停车波、启动波等), 质点的运动方向(纵向)与波的传播方向(纵向)平行, 故而传统交通波是纵波; 因此在实际非机动车交通流中, 换道波和传统交通波是并存的, 它们共同影响着后车的驾驶行为。本文定义前车换道引发的后方单位元胞长度内的换道的最大车辆数为换道波的振幅, 换道波振幅的大小与车道数有关, 车道越多, 振幅越大, 换道波的能量越大, 传播的就越远。图1为本文设计的换道波形成机理和传播图示, (x, y)为每个元胞(车辆)的坐标, 椭圆圈中的部分(①、②)为换道波发生的位置; 其中①中车辆(1, 2)作为换道波的波源首先引发了(2, 2)、(2, 3)两辆车的换道, 振幅为2个单位, 其次车辆(2, 2)、(2, 3)又引发了车辆(3, 1)的换道, 振幅为1个单位, 最后车辆(3, 1)未引发车辆(4, 3)或(4, 1)换道, 换道波传播到这里消失, 即换道波在传播过程中受到了阻尼而不断衰减, 最终消失; ②中车辆(7, 1)作为一个新的换道波的波源, 引发后方车辆(8, 2)、(9, 2)的换道, 之后会由于第9列元胞后方长距离内无车辆, 即换道波没有了传播介质, 使得换道波消失。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 换道波形成机理和传播图示Fig.1 Formation mechanism and propagation of lane-changing wave

(2)局部最大熵思想引入换道规则

电动自行车换道相对比较随意, 目的却都是为了充分利用道路资源, 若不考虑各个车道之间的微弱差别, 则每个车道被车辆占据的概率是相同的; 总体上, 车辆将会均匀分布在各个车道上(即每条车道上车辆数近似相同), 因为这时的熵值最大, 道路资源得到最充分的利用, 因此道路上大多数车辆的换道行为将会向这样的方向进行, 即为熵增方向。

考虑到实际中电动自行车驾驶员在换道时不会看的太远, 即驾驶员一般只是注意到前方几个元胞长度内各车道的空闲元胞数量, 从而产生换道的期望。结合电动车的最大速度3 cells/s, 本文设定驾驶员在分析换道时考虑前方三个元胞长度, 即为“ 局部最大熵” 。

为了体现电动自行车流换道波的特点, 在换道更新时采用串行更新的方式。简单的串行更新会在一个时间步内, 依次完成道路上从头车到尾车的所有车辆的更新, 而换道波的波速和能量有限, 不可能在单位时间步内传播这么远。为此, 引入熵增换道概率的概念, 即满足熵增换道条件时, 将会以一定的概率换道, 而不是一定换道。熵增换道概率对于换道波来说, 将是一种阻尼, 它会使得前车引发的换道波振幅不断削弱, 最终使得换道波消失。

在这样的条件组成的仿真系统中, 每一辆车都会根据前方一定范围内的交通状况, 决定是否换道, 并可能作为换道波的波源, 引发一段长短不一的换道波。

(3)局部最大熵原理下的换道规则

局部最大熵原理下的换道规则文字简述如下:

向左(右)换道条件:①当前车道左(右)侧无车辆; ②当前车道前方三个元胞内的车辆数多于左(右)侧; ③由熵增换道概率决定是否向左(右)换道; 表1是局部最大熵原理下, 电动自行车换道规则的严格数学表述。

表1中, N_l(N_r)表示与当前元胞左(右)侧相邻的元胞是否可用, N_l(N_r)=0, 意味着左(右)侧被车辆占据或者已无车道, 处于不可用的状态, 相反, N_l(N_r)=1, 则左(右)侧元胞可用; Nlf3( Nrf3)表示当前元胞左(右)侧相邻车道前方三个元胞长度内空元胞数; Flag=1, 表示产生向左换道的期望, Flag=0, 表示不产生换道期望, Flag=-1表示产生向右换道的期望; P_e为熵增换道概率, 若change=true, 且具有换道期望则发生相应的换道, 否则不换道。

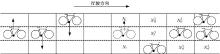
如图2所示, 灰色的电动自行车为当前要更新的车辆, 图中N_l=N_r=1, Nlf3= Nrf3=2, Nf3=1, 依据表1所示的换道规则, Flag=1, 当前车辆有向左换道的期望; 若熵增换道概率为1(换道波的阻尼为0), 该车将会向左换道, 并依次引发了后方三辆车的换道, 即换道行为在向后方传播, 换道波产生, 灰色车辆即为换道波的波源; 由此可见本文设计的换道规则, 能够模拟电动自行车流中的换道波。

需要说明的是, 对于靠右行驶的地区(例如中国大陆), 在左右两侧换道条件相同时, 优先向左换道, 对应的串行换道横向更新的顺序从左到右, 表中设计的规则即为这种情况, 也是后文仿真中采用的规则; 而对于靠左行驶的地区(如日本), 则优先向右换道, 串行换道横向更新顺序从右向左。

表1

Table 1

表1(Table 1)

表1 局部最大熵原理下的换道规则 Table 1 Lane changing rule based on local maximum entropy principle Nl≠ 0 and Nr≠ 0 Nl=0 and Nr=0 Nl≠ 0 and Nr=0 Nlf3> Nf3 and Nlf3≥ Nrf3 Flag=1 Nrf3> Nf3 Flag=-1 Nlf3> Nf3 Flag=1 Nrf3> Nf3 and Nrf3> Nlf3 Flag=-1 其他 Flag=0 其他 Flag=0 其他 Flag=0 Nl=Nr=0 Flag=0 If rand()< Pe, then change=true;

表1 局部最大熵原理下的换道规则 Table 1 Lane changing rule based on local maximum entropy principle

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 换道规则以及该规则下的换道波Fig.2 Lane changing rule and its change wave

仿真中设置道路长度为100个元胞长度(200 m), 采用周期性边界条件, 车辆在道路上的位置的初始分布为随机分布。抛弃前20 000个时间步, 取接下来的5000个时间步用于分析和计算绘图。对于2.2节中的仿真结果图, 在无特别说明时, 车道数取3, 熵增换道概率取0.7, 慢化概率取0.1。画流量密度图时, 密度(density)为道路上平均单位元胞被占据的车辆数(vehicles· cells^-1), 速度为车辆在单位时间步内前进的元胞个数(cells· s^-1), 流量利用公式flow=V_ave· density计算得出(vehicles· s^-1), 其中V_ave为5000个时间步内道路上所有车辆的平均速度。作换道率-密度曲线时, 换道率是指单位时间平均每个车辆的换道次数(次· (辆· s)^-1), 具体计算时, 用的是5000个时间步内, 考虑道路上所有车辆换道次数的平均。

下面分别讨论确定性以及随机性条件下, 不同的参数设置对流量-密度以及换道率-密度关系图的影响, 其中确定性条件是指慢化概率的等于0, 随机性条件下慢化概率大于0, 变化的参数包括慢化概率、车道数、熵增换道概率。

2.2.1 确定性条件下不同车道数的流量密度关系分析

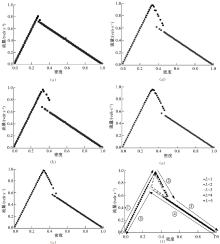
首先从图3(f)中可以看出, 在确定性条件下, 随机化的车辆位置初始分布, 当车道数不同时, 流量密度关系图的线型是一致的; 在图3(f)中, ④⑤(粗实线)所指示的曲线与单车道的致密阻塞初始分布下的流量密度图^[4]一致, ①②③(细实线)所指示的曲线与单车道均匀初始分布的流量密度图^[4]一致。

密度处于区间(0.25, 0.5)的区域为亚稳态区域, 中间的虚线三角形所指示的区域即为回滞三角形。对于落在回滞三角形上面两条边的点, 表示处于高流量状态, 尚未发生“ 流量崩溃” , 稳定后的车辆分布为均匀分布; 落在下面一条边上的点, 表示处于相应密度的低流量状态, 即发生了“ 流量崩溃” , 稳定后部分路段处于阻塞状态, 另外一部分处于近似自由流的状态。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 确定性条件下不同车道数对应的流量密度关系图Fig.3 Fundamental diagrams of different lane numbers in deterministic cases

图3(a)~(e)为图3(f)各个车道下的分解图, 密度步长为0.01, 亚稳态区域(0.25, 0.5)点的总个数为24个。深黑色标记的表示落在高流量分支的点, 浅灰色的表示落在低流量分支的点, 不同车道数对应的深黑色点的数量及其占亚稳态区域总点数的比例如表2所示。

表2

Table 2

表2(Table 2)

表2 不同车道数对应的高流量点的个数及其占比 Table 2 Numbers and percentage of high flow points corresponding to different lane numbers 车道数 1 2 3 4 5 高流量点个数 3 11 17 19 20 高流量占比/% 12.50 45.83 70.83 79.17 83.33 注:已通过重复仿真验证, 相同的仿真条件下高流量点个数不发生明显变化。

表2 不同车道数对应的高流量点的个数及其占比 Table 2 Numbers and percentage of high flow points corresponding to different lane numbers

从表2中可以看出, 随着车道数的不断增加, 落在高流量分支的点的个数也在不断增加, 但增加变得越来越慢, 当车道数达到4以后, 处于高流量的点个数及其占比不再显著的增加。说明随着车道数量的增加, 对于随机的车辆位置初始分布, 亚稳态区域的流量落在高流量分支的可能性越来越大, 并在车道数增加到4时, 达到饱和。即车道数的增加使得亚稳态区域流量崩溃的可能性降低, 车流更加稳定, 更加高效, 但在车道数超过4条时, 车道数再增加对流量变化的影响已经很小了。为此, 我们建议在电动车流量较大的地区, 设置4条电动车道为宜, 这样能使得车流更大可能的处于高流量分支, 从而提高道路使用效率和服务水平。

2.2.2 随机性条件下不同参数对应的流量-密度关系以及换道率密度关系分析

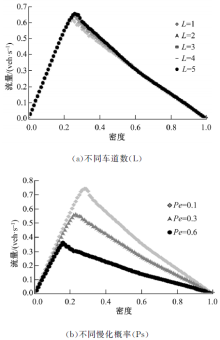
图4(a)为随机性条件下, 不同车道数对应的流量密度关系图, 从中可以看出, 在密度为0.25~0.5之间的亚稳态区域, 流量无一例外的落在了确定性条件下的低流量分支以下(通过流量的峰值< 0.7可以看出); 同时, 车道数的增加, 只能很微弱的提高亚稳态区域的小部分流量。但这与2.2.1中的结论并不矛盾, 在2.2.1中我们发现, 在确定性条件以及车辆位置随机化的初始分布下, 车道数的增加会使得亚稳态区域的密度对应的流量落在高分支的可能性增加, 这是不考虑慢化概率的情况下, 而图4(a)中的结果是在慢化概率为0.1的情况下, 即道路上平均每个时间步都有200× 0.1=20辆车发生随机慢化。此时车辆慢化引起的“ 幽灵堵塞” 已非车道数增加所能化解, 所以即使车道数增加, 亚稳态区域的车流量仍难以提升。对于缓解此种情况引起的交通拥堵, 应从减小慢化概率的角度入手, 改善交通状况。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 随机性条件下, 不同参数对应的流量密度基本图Fig.4 Fundamental diagrams of different parameters in stochastic cases

图4(b)为不同的慢化概率, 对应的流量密度关系图。从图中可以看出, 慢化概率的增加不仅显著的降低了最大流量值, 同时也会使得在流量在较小密度下达到峰值。这是由于慢化概率的增加使得车辆的速度增加变得困难, 降低变得容易, 道路上任意车辆很容易就成为其他车辆的障碍, 结果使得车辆整体速度显著降低, 道路流量降低。

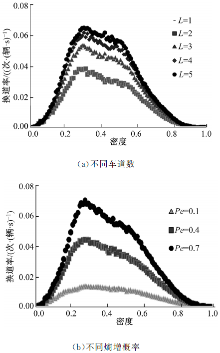
从图5(a)(b)中可以看出, 无论是改变熵增换道概率, 还是车道数, 换道率— 密度的曲线图的形状基本是保持不变的, 类似一个倒着的“ U” 形, 最初密度的增加使得换道率急剧的上升(0~0.25), 而后密度的增加使得换道率微弱的减小(0.25~0.5), 最后密度的增加使得换道率急剧的降低(0.5~1)。最初换道率增加是由于密度增加, 车辆受阻碍的机会变多, 但密度还不过大, 旁边车道仍有空闲, 于是车辆为了提高速度会向周围车道变道, 换道率显著增加; 当密度增加到一定程度, 道路上车辆增多, 周边车道也被占据, 向周边换道提高速度的机会变少, 于是换道率稍稍的降低; 最后道路上车辆数已经很多, 周边车道与本车道一样拥堵, 换道已经没有意义, 换道率急剧下降。从换道波的角度来说, 最初换道率的增加, 是由于密度增加, 换道波的波源增多, 而换道波能够传播也必须具有传播介质, 密度增加使得更多的车辆引起的换道波能够有传播介质将其传播下去, 换道率显著增加; 其次换道波的波源减少, 传播介质增多, 换道率微弱的减小; 最后换道波波源显著减少, 且阻尼增大, 换道率显著降低。

具体地说, 图5(a)说明熵增换道概率直接影响着换道率, 熵增换道概率的小幅增加, 即可大幅提高换道率; 事实上, 作为换道波的阻尼, 熵增换道概率越大, 则换道的阻尼越小, 传播的越远, 换道次数越多。图5(b)显示了不同车道数对换道率的影响, 车道数增加, 换道波的振幅增大, 波传播的更远, 换道次数增多。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 随机性条件下不同参数对应的 换道率-密度关系图Fig.5 Diagrams of relationship between lane change rate and density of different parameters in stochastic cases

(1)数据收集

之前关于的非机动车元胞自动机仿真的研究虽然很多, 但却少有实地调查数据验证。本文选择了郑州市这样一个电动自行车非常多的城市作为调查地点, 先后选取了不同道路宽度的两条路段进行录像调查, 提取数据, 如图6所示。选择的道路都是坡度很小, 并且没有机动车干扰的隔离路段。各调查地点道路的属性数据见表3前半部分。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 调查地点录像截图Fig.6 Photos of the camera’ s view of two sites

(2)参数标定

慢化概率的参数标定:慢化概率影响电动自行车的行驶速度, 从而影响整个电动自行车道的流量, 从仿真结果图4(b)中, 也可以看出慢化概率对电动自行车的流量具有显著的影响。为了获取一个合适的慢化概率, 本文利用仿真的不同慢化概率下的流量密度图与实测的流量密度图作对比, 寻求契合度最高的仿真的流量密度图对应的慢化概率作为最优慢化概率。另外, 选取流量的平均绝对误差(MAPE_flow见式(6))作为评价仿真的流量密度图与观测的流量密度图的契合度高低的指标^{[10, 11]}, 从而得到不同慢化概率下的平均绝对误差如图7(a)和7(c)所示, 流量的最小平均绝对误差及其对应的慢化概率见表3。

MAPE_flow=1M∑j=1MQ^(j)-Q(j)Q(j)×100%（6）

式中: Q^(j)为对于第j个样本密度仿真的电动自行车流量; Q(j)为第j个样本密度观测的电动自行车流量; M为样本总数。

熵增概率的参数标定:在局部最大熵模型中, 熵增概率的大小主要是影响驾驶员的换道行为, 即不同的熵增概率对应的换道率有着显著的不同, 如图5(b)所示。而要获取合适的熵增概率, 就需要根据不同熵增概率下换道率与密度关系图与实际的换道率-密度关系图对比, 从而发现最优熵增概率。为了评价每个熵增概率下, 仿真的换道率-密度关系图与实际换道率-密度关系图契合度, 本文使用式(7)换道率的平均绝对误差作为度量指标。

表3

Table 3

表3(Table 3)

表3 调查路段属性及拟合最优误差 Table 3 Property of field survey sites and result of calibrating slowdown probabilities with MAPEs 编号 路段名称 车道宽度/m 车道数量 标定的慢化概率 流量的最小平均 绝对误差/% 标定的熵增概率 换道率的最小平均 绝对误差/% 1 二七路 2.72 2 0.05 24.48 0.7 14.02 2 正兴街 4.05 3 0.1 15.11 0.7 7.84

表3 调查路段属性及拟合最优误差 Table 3 Property of field survey sites and result of calibrating slowdown probabilities with MAPEs

MAPE_change=1M∑j=1MC^(j)-C(j)C(j)×100%（7）

式中: C^(j)为对于第j个样本密度仿真的电动自行车换道率; C(j)为第j个样本密度观测的电动自行车换道率。图7中(e)(g)分别为两车道和三车道情况下, 不同的熵增换道概率对应的平均绝对误差。最小平均绝对误差及其对应的熵增概率见表3。

最后需要说明的是, 经过多次仿真发现, 熵增换道概率主要是对电动自行车流的微观换道行为影响很大, 对流量密度关系图影响很小, 所以在第一步仿真获取流量密度图标定慢化概率时, 并不太需要清楚此时最合适的熵增换道概率是多少, 可取熵增换道概率为0.4~0.9(本文中取熵增换道概率为0.8), 都是可以得到最优的慢化概率。而在标定熵增换道概率时, 由于此时已知不同车道的最优慢化概率, 所以选取上一步标定的最优慢化概率, 作为仿真时使用的慢化概率, 生成换道率密度关系图, 得出最优的熵增换道概率, 由于换道率与密度关系图会受到慢化概率的影响, 所以本节参数标定的顺序是不可逆的, 即必须先标定出慢化概率, 再标定熵增概率。事实上, 已经过仿真验证, 若利用第二步标定出的熵增概率再作为第一步仿真时的熵增概率进行回代, 仍会得出的相同最优慢化概率。

(3)模型对比

选取表3中对应流量的最小平均绝对误差的慢化概率作为仿真采用的慢化概率, 对应换道率的最小平均绝对误差的熵增换道概率作为仿真采用的熵增换道概率, 分别做出多值模型、最大熵模型、动态地场模型的流量密度关系图, 与观测值对比, 同时也将观测的不同密度下的换道率与仿真结果对比, 如图7所示。图7分别展示了2车道和3车道的情况下, 不同的仿真模型与观测值的对比, 结合表4发现, 本文模型与多值模型^[2]有着极为相似的结果, 两车道模型精度约为24%左右, 三车道模型精度约为15%, 相比动态地场模型^[4](两车道39.27%, 三车道24.06%)对观测数据的拟合有着更高的精度; 另外通过图7(f)、(h)可以看出, 本文提出的是一种考虑换道的模型, 无论是双车道还是三车道, 模型都能很好地反映实际的换道率与密度的变化关系, 从而克服了多值模型不考虑换道、不利于进一步研究车辆微观行为的弊端, 因此也优于多值模型。

图7

Fig.7

	Figure Option ViewDownloadNew Window
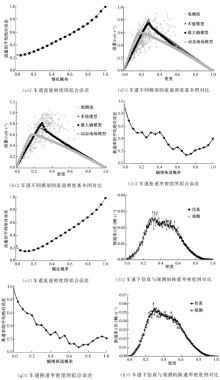	图7 不同密度下的换道率观测与仿真结果对比Fig.7 Observe and simulation results comparison of lane change rate indifferent density

表4

Table 4

表4(Table 4)

表4 不同车道下不同模型的精度对比 Table 4 Accuracy comparison of different models in different lanes % 车道数 最大熵模型 多值模型 动态地场模型 2车道 24.48 24.63 39.27 3车道 15.11 15.57 24.06

表4 不同车道下不同模型的精度对比 Table 4 Accuracy comparison of different models in different lanes %