波形钢腹板组合梁桥是一种新型组合结构, 近些年在日本已有诸多应用, 结构形式从简支梁、连续梁逐渐应用到埃塔斜拉桥、斜拉桥等。由于波形钢腹板组合箱梁桥自重为混凝土箱梁桥的20%~30%, 相比同等跨径的钢箱梁或混凝土箱梁造价上也可节约20%~30%, 从2005年以来, 中国也相应地开展了一些有关波形钢腹板组合梁桥的研究和应用, 在建和已建桥梁达到30余座。桥梁的结构形式同样从简支梁、连续梁扩展到连续刚构、矮塔斜拉桥、斜拉桥等, 截面形式也从最初的单箱单室扩展到单箱多室、多箱多室。桥梁宽跨比超越0.5的情况较多, 桥梁宽度也向超宽方向发展, 已有大跨、超宽的桥梁出现, 如日本的日见梦矮塔斜拉桥(91.8+180+91.8)m、日本栗东部分桥(137.6+170+115+67.6)m、日本矢作川斜拉桥(173.4+2× 235+173.4)m、江西南昌朝阳大桥六塔斜拉桥(79+5× 150+79)m、山西运宝黄河大桥三塔斜拉桥(110+2× 200+110)m、河南朝阳沟大桥双塔斜拉桥(118+188+118)m等。

与普通混凝土箱梁类似, 波型钢腹板组合箱梁的顶底板同样存在弯曲应力分布不均匀现象, 称之为“ 剪力滞效应” 。有关剪力滞效应的研究, 已有一些文献相继出现^[1], 简单梁式结构单箱单室(直腹板或斜腹板)方面的研究较多, 但是单箱多室超宽形式波形钢腹板斜拉桥剪力滞效应的研究还没有, 使用空间网格分析方法分析其剪力滞效应亦是尚属首次。因此, 有必要对多箱室波形钢腹板斜拉桥剪力滞效应进行分析和精细化分析方法进行模拟, 为此类结构的应用推广提供技术支持^{[1, 2, 3]}。

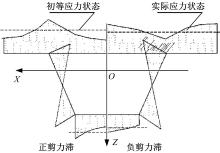
在对称纵向弯曲荷载作用下, 如果箱梁翼板具有初等弯曲理论中所假定的无限抗剪刚度(即平截面假定)的话, 则翼板中所产生的纵向应力沿板宽方向将是均匀的。然而大多数情况下, 特别是对于翼缘较宽的箱型梁来说, 由于翼板中的剪切变形导致纵向正应力沿翼板宽度呈不均匀分布, 其间存在传力的滞后现象, 它与初等梁理论所表示的应力之间的差异, 称为“ 剪力滞效应” , 如图1所示。如果翼缘板与腹板交界处的法向应力大于初等梁理论的计算值, 称为“ 正剪力滞” , 反之, 则称之为“ 负剪力滞” 。这种弯曲应力分布不均匀的现象, 足以使混凝土箱梁局部位置产生应力集中, 甚至开裂^{[4, 5]}。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 剪力滞现象Fig.1 Phenomenon of shear lag

剪力滞系数的定义:λ =考虑剪滞效应所求的正应力/按初等梁理论求的正应力, 该定义中的分母在平面杆系分析中表示的是截面的平均正应力。本文剪滞系数的计算是根据翼板正应力图形下的面积除以翼板的宽度, 得到一个相似于按初等梁理论求得的应力平均值, 再用这个应力平均值去除横截面上各点的实际应力, 即得到横截面上各点的剪滞系数, 它既类似于经典定义中的剪滞系数, 同时也考虑了空间结构分析的特点, 即:

σ0=∑i=1nσibi/b(1)

剪力滞系数λ =σ /σ ₀; 最大剪力滞系数λ _max=σ _max/σ ₀, 式中σ 为三维实体单元节点的纵向平均正应力; b_i为单元节点横向距离; σ _max为有限元计算的翼板最大应力值; σ ₀为初等梁理论计算的正应力; n为顶底板划分的单元数量。

从式(1)中可知, 翼缘有效分布宽度是根据应力体积相等的原理换算得来的。有效宽度与实际宽度之比称为有效宽度比, 它反映翼板应力分布不均匀程度。因此, 目前的工程设计多采用折减后的截面抗弯惯矩, 按初等梁的弯曲理论计算梁的纵向弯曲应力与挠度。

对于波形钢腹板组合梁桥的分析, 通常采用空间杆系模型、平面梁格法与局部实体分析相结合的方法。但是, 空间杆系模型缺乏对空间效应的精细化分析, 比如:宽箱梁的平截面假定、有效分布宽度、偏载系数、各个腹板的内力分配、横向分布系数等问题; 平面梁格法由于在等效原理上的近似性, 不能准确反映箱形组合梁的剪应力分布和顶底板局部受力; 实体分析很难与总体计算完全结合, 分析结果是总体应力结果, 与现行规范的内力配筋设计方法不匹配, 往往只在局部分析中应用。所以空间杆系模型、平面梁格模型及实体模型不能全面、完整的反应出结构的受力特性。针对目前多箱室波形钢腹板组合梁的计算分析不足的情况, 引入空间网格分析方法。网格模型将组合梁截面视为由若干块板组成, 对每一块板进行梁格划分, 用划分后的梁格来等效代替每块板的受力。相比梁格法, 空间网格划分更细。由于将顶板划分的更密, 可以分析出顶板的各梁格在剪力滞效应下的应力, 且不用计算有效宽度。刚性扭转通过空间网格之间的相互共同作用反映在各个梁格的剪应力上, 同样可以实现在荷载作用下截面的畸变分析及截面各个板件的横向弯曲变形。它能够分析组合梁截面在偏心荷载作用下的各种变形形态。空间网格模型输出的结果是各个梁格的内力、应力及位移, 可以方便得到结构不同部位的受力状态, 从而有针对性的加强构造配筋, 对实际工程的设计分析有重要意义^{[6, 7]}。

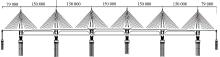
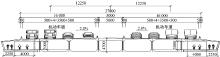
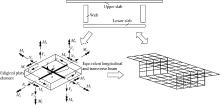
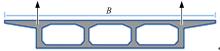
本文所研究的波形钢腹板组合箱梁六塔斜拉桥的纵向及横向构造及尺寸参见图2和图3, 波纹钢腹板标准段如图4所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 大桥跨径布置图Fig.2 Layout of bridge span

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 梁模型基本尺寸(单位:mm)Fig.3 Basic dimensions of beam model

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 波形钢腹板构造示意图(单位:mm)Fig.4 Schematic diagram of structure of corrugated steel webs

通过实桥计算验证, 空间网格模型可以得到多箱室箱梁完整的应力。在恒荷载及预应力作用下, 分析了多塔斜拉桥边、中跨关键截面顶底板剪力滞效应。通过分析, 总结出关键截面的剪力滞效应分布规律, 剪力滞系数沿纵向分布规律等, 进而验证了空间网格分析方法分析多塔波纹钢腹板组合梁斜拉桥剪力滞效应的有效性和准确性, 也为精细化的设计提供了有力的指导。

在结构分析中, 可以将复杂的桥梁结构离散成由多块板构成, 再将每一个板元由十字交叉的正交梁格组成, 以十字交叉的纵横梁(6DOF梁单元)的刚度等代成板的刚度, 一片正交梁格就像是一张“ 网” , 一个结构由多少块板构成, 就可以用梁格表示成多少张“ 网” 。这样, 空间桥梁结构可以用空间网格来表达。如图5所示, 一个单箱单室箱梁截面可以分解为顶板、底板以及多块腹板构成, 箱形截面梁所离散成的“ 板” 就可以用正交梁格模型来模拟。由于这些“ 板” 位于不同的平面内, 代表它们的正交梁格也在不同的平面内(对于弯梁桥为曲面), 不同平面内的正交梁格将箱形截面梁离散为一个空间“ 网” 状模型, 可以形象的称为“ 空间网格” 模型^[8]。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 空间网格模型简化原理示意Fig.5 Schematic diagram of spatial grid model

2.1 结构离散

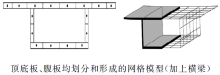
建立空间网格模型时, 纵向可依据单梁有限元划分方式划分(即考虑的因素通常为结构受力、自然施工划分等); 截面内部划分的疏密程度宜根据截面形式和计算要求确定, 它反映了表达空间效应的精细化程度。空间网格模型截面划分时将腹板分块。腹板与顶、底板均划分, 对应的截面划分及网格模型如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 空间网格模型的截面划分方式示意图Fig.6 Schematic diagram of cross section division mode of spatial grid model

2.2 离散后截面特性计算

按图7离散后所得的空间网格模型中, 截面主要有以下三种:腹板整体截面、腹板划分截面、纵横向顶底板划分截面, 如图7所示。这些截面及特性计算与传统梁单元截面特性计算一致, 由离散后实际截面尺寸计算。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 空间网格模型常用截面Fig.7 Common cross section of spatial grid model

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 空间网格模型常用截面截面特性计算示意图Fig.8 Schematic diagram of calculation of common cross section characteristics in spatial grid

这里以图8所示的矩形截面为例, 说明网格模型中常用截面的截面特性计算方法:

轴向面积：

Ax=bh（2）

剪切面积：

Ay=Az=bh(3)

抗弯惯矩：

Iz=b3h12; Iy=bh312（4）

截面划分后, 划分截面的抗扭惯矩对整体截面的影响相当有限, 故抗扭惯矩可采用如下简化公式计算:

IT=4IzIyβ(Iz+Iy)β=1.3~1.6（5）

2.3 效应计算及表达方式

空间网格模型即将薄壁箱形截面视为由若干块板组成, 对每一块板进行网格划分, 用划分后的网格来等效代替各个板的受力。由于空间网格模型将顶底板划分的较密, 可以分析出顶底板的剪力滞效应, 且不需要计算有效分布宽度。箱梁的刚性扭转效应通过空间网格纵横单元之间的相互作用, 反映在各个梁格的剪应力分布上; 空间网格模型同样可以实现在荷载作用下截面的畸变分析以及截面各个板件的横向弯曲变形分析。

在用空间网格模型中, 截面荷载效应分担如下:①箱梁截面的纵向效应(如轴力、弯矩)由纵向梁格承受; ②箱梁截面的横向效应(如畸变、活载横向效应等)由横向梁格承受; ③箱梁截面的扭转、畸变效应转化为腹板梁格的剪力。

在空间网格模型中, 通过分析计算可以得到组成网格的各部分截面(腹板整体截面或腹板划分截面)的内力(包括轴力、弯矩、剪力、扭矩), 单元内力按照单元刚度进行分配, 对不同的截面形式, 荷载效应的计算方式分别如下所述。

(1)划分截面

一般用于模拟网格模型中的箱梁顶板和底板, 主要承受轴力N_x、N_y, 面内剪力V_xy以及面外弯矩M_x、M_y。如图9所示, 沿着单元厚度均匀分布的薄膜效应和顶底板的局部荷载效应(沿着单元厚度线性变化的出平面弯曲正应力)可以通过“ 划分截面” 完全体现出来。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 空间网格模型“ 划分截面” 效应计算示意图Fig.9 Schematic diagram of“ division section” effect clculation of spatial grid model

(2)面外正应力

σx=MyzIy（6）

σy=MxzIx(7)

式中:σ _x为截面x向正应力; σ _y为截面y向正应力; z为计算正应力应力点至截面重心轴的距离, 重心轴以上取正值; I_x、I_y为垂直于y轴或x轴的截面绕各自截面重心轴惯性矩; M_x、M_y为垂直于y轴或x轴的截面绕各自截面重心轴弯矩。

(3)面内正应力

σx-m=NxAx=Nxbxhx(8)

σy-m=NyAy=Nybyhy（9）

式中:σ _x-m为截面中面x向正应力; σ _y-m为截面中面y向正应力; b_x、b_y为截面中垂直于x向或y向截面的宽度; h_x、h_y为截面中垂直于x向或y向截面的高度。

(4)面内剪应力

τxy=Vxybxhx（10）

(5)面内主拉应力σ _t和主压应力σ _c

按下式计算:

σtσc=σx-m+σy-m2±σx-m-σy-m22+τxy2（11）

空间网格模型不仅能够准确分析复杂结构的空间受力状态, 而且其输出的数据结果(以单元杆端力的方式输出)是各个梁格单元的内力、应力及位移, 可以方便得到结构不同部位的受力状态, 并且和现行桥梁设计规范直接对应, 从而有针对性的指导桥梁各部分的配筋设计, 对实际工程的设计分析有重要意义。

2.4 适用范围

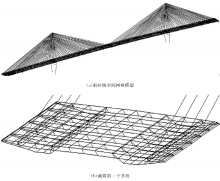
空间网格模型中的各块“ 板” 共同作用构成箱形截面梁独特的全截面抗弯、抗扭与抗剪刚度。这些板可以是钢的, 可以是混凝土的, 或其它任意材料的。于是, 这些板元便可以“ 组合” 成全混凝土截面、全钢截面、部分是钢部分是混凝土的截面(钢-混凝土叠合梁)、以及其他任意几种不同材料组成的截面。所以空间网格模型适用于弯桥、斜桥、宽桥、组合梁等各种桥型, 不受具体结构形式的限制, 用空间网格法建立的桥梁结构模型如图11所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 空间网格模型示例Fig.10 An example of spatial grid model

2.5 剪力滞效应的规范与空间网格分析方法区别

针对宽翼缘桥梁的剪力滞效应已有许多研究工作, 部分成果已经纳入了各国设计规范之中, 即在分析宽翼缘桥梁(工字梁、T形梁、薄壁箱梁)的上部结构时, 采用有效分布宽度的方法来考虑应力峰值。对于箱梁正应力计算也规定了相应的有效分布宽度。有效分布宽度是通过对翼缘宽度的折减来包络剪力滞效应引起的应力峰值, 正、负剪力滞效应如图1所示, 但这种方法只能粗略考虑剪力滞效应, 且该有效分布宽度仅适用于简单结构的简单受力情况, 即结构一次落架的受弯分析。

对于多腹板的宽箱梁桥, 应用有效分布宽度时就会出现如下问题:无法得到一个统一的、也较为准确的“ 有效分布宽度” 。例如对图11所示结构的剪力滞效应, 其施工过程中的结构自重及其预应力、拉索等作用下的剪力滞效应并不相同, 规范实际上并没有统一依据可以采用。图11中箭头表示斜拉索索力。预应力钢束和斜拉索的剪力滞效应实际上已经转化为从荷载作用点到截面平均分布的荷载传递问题。值得注意的是剪力滞效应在扁平宽梁中才比较明显, 同样的截面应用于不同跨径其剪力滞效应相差较大^{[9, 10]}。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 宽箱梁截面的索结构桥Fig.11 Wide box girder cross section of a cable stayed bridge

剪力滞系数(或有效分布宽度)与结构形成有关。目前规范方法仅适用于某种确定结构状态承受竖向力的情况(即受弯情况, 包括预应力产生的弯矩), 并不适用于水平力(如预应力的轴向力等)。如果结构形成时的施工阶段均采用成桥后结构的剪力滞系数(如结构采用悬臂施工时), 就与实际情况不相符合。预应力(轴向力)的作用实际上是集中力的扩散效应, 与受弯有效分布宽度的概念并不相干^{[9, 11, 12]}。

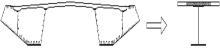
对于叠合截面桥梁结构, 传统的初等梁理论计算方法大多采用单主梁模型, 如图12所示。利用有效分布宽度和换算截面的办法将叠合梁结构等效为工字形截面, 对叠合梁进行分析和设计。实际上此种计算方法严重忽视了主梁内力和应力分布的空间特点, 既无法得到一个较为准确的“ 有效分布宽度” , 更无法考虑混凝土桥面板面内的水平剪应力, 从而影响到叠合梁桥面板的配筋^{[13, 14, 15]}。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 叠合箱梁截面等效为工字形截面Fig.12 Equivalent I-shaped cross section of composite box girder

由上述分析可得, 采用“ 有效分布宽度” 概念考虑剪力滞效应存在疏漏:即只关注了顶底板和腹板的正应力及腹板的剪应力, 对于顶底板的剪应力和剪力流都未加以关注, 从而导致在设计配筋过程中无法完整考虑顶底板的面内主应力。实际桥梁结构中存在顶底板中的斜裂缝, 正是由于板面内主拉应力超标而引起的开裂, 这一问题在采用初等梁理论的传统设计计算方法里面没有反映出来^{[15, 16]}。

空间网格模型将箱梁划分为N个板件, 可以计算出板件面内和面外完整的应力, 每块板件中包含三层应力, 表1可诠释空间网格模型分析板件应力的完整性。由此, 可以得出箱梁翼缘板上应力的分布规律, 避免了宽箱梁采用单一有效分布宽度来设计的缺陷, 弥补规范的不足。

表1

Table 1

表1(Table 1)

表1 箱梁结构应该关注的9项验算应力 Table 1 It should pay attention to 9 calculating stress of box girder structure 构件 受力方向 应力特征 与传统关注应力比照 顶板 纵向面外上缘 一维应力 整体截面上缘应力 横向面外上缘 一维应力 另外进行桥面板局部计算 横向面外下缘 一维应力 另外进行桥面板局部计算 中面 二维应力 没有包含(同叠合梁) 底板 纵向面外下缘 一维应力 整体截面下缘应力 横向面外上缘 一维应力 主要为计算底板钢束的外崩力, 横向面外下缘 一维应力 简化计算方法不完善 中面 二维应力 没有包含(同叠合梁) 腹板 中面 二维应力 腹板主应力

表1 箱梁结构应该关注的9项验算应力 Table 1 It should pay attention to 9 calculating stress of box girder structure

工程实例桥型立面图如图2所示, 南昌朝阳大桥主桥为跨长908 m(79+5× 150+79)m的波纹钢腹板混凝土箱型单索面斜拉桥。考虑到全桥的复杂性, 利用6自由度空间网格模型+单梁模型对该桥进行受力状态分析。全桥模型如图13(a)所示, 计算模型由空间6自由度梁格系组成, 全桥共分6493个节点和13 539个单元。横隔梁在模型计算时只计入结构, 重量按均布荷载计入。网格模型部分, 主桥支座采用支座连杆单元模拟, 上部节点连接到腹板单元下节点上; 单梁部分, 支座通过横向刚臂连接到主梁节点上。全桥支座连杆的下节点连接到桥墩上部悬臂单元的节点上。支座单元的截面抗弯刚度修改为零。桥梁整体坐标系的选取为:原点设在一侧端横梁的中点, 方向规定根据右手规则, x方向沿桥梁纵向, y方向为竖直向上, z方向沿桥梁横向。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 空间网格+单梁计算模型Fig.13 Calculation model of space mesh+single-beam

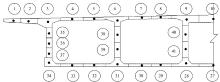
箱梁断面的划分和节点情况, 如图14所示(虚线表示截面单元的分割线), 沿纵向共分为48根纵梁(考虑对称性, 图中只示意截面一半):波纹腹板划分为2~3根矩形板单元, 可以得到截面上、下缘位置的正应力及主应力; 顶、底板划分为多个板单元, 可以得出板单元上、下缘的正应力及单元的面内主应力。图14中圆圈内数字表示纵向单元编号, 黑点表示纵向单元形心所在位置, 后续计算结果中以“ 纵梁-1” 表示1号纵梁的结果, 其他纵梁结果以此类推。在空间网格模型当中, 修改代表波纹钢腹板的纵向单元纵向刚度, 按照理论公式计算的折减倍数, 将单元轴向刚度面积折减883倍, 其余几何特性及材料参数不进行修正。网格模型中, 腹板竖杆单元的截面为图15所示两种截面类型, 面外刚度所选择的腹板竖杆单元对应截面如图16所示。

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 箱梁断面划分示意图Fig.14 Schematic diagram of division of box beam section

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 竖杆单元截面图Fig.15 Cross section of vertical bar unit

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 竖杆单元面外刚度截面Fig.16 Out-plane rigidity cross section of vertical bar

沿全桥纵向在每个节段横隔梁位置, 用图17中的横向网格单元来模拟箱梁截面的横向框架效应。

图17

Fig.17

	Figure Option ViewDownloadNew Window
	图17 箱梁断面横向网格单元位置示意图Fig.17 Schematic diagram of transverse mesh unit location in box beam section

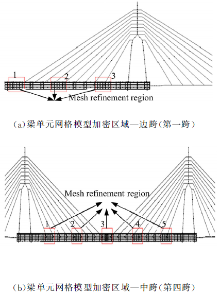
同时, 对边跨(第一跨)及最内侧中跨(第四跨)实施了网格化, 对网格化跨段中的1#、5#、9#关键节段进行细化(考虑钢加劲肋、钢横梁、虚拟横梁、节段接口等)。在后续的计算结果部分将给出这些位置箱梁顶板、底板单元在横向的受力。

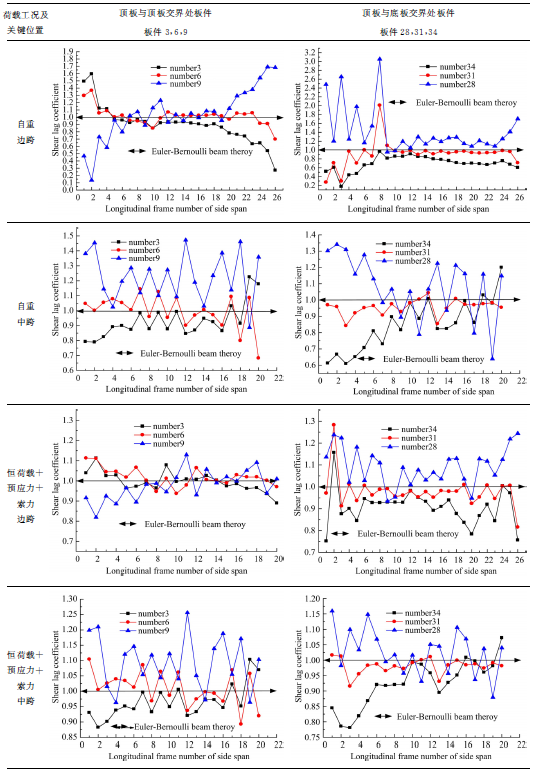
箱梁的剪力滞效应通过剪力滞系数表达, 实例中斜拉桥采用了单箱多室截面形式, 分析工况分为:纯自重作用及恒载、桥面板纵横向预应力、斜拉索索力共同作用情况下的结构一次落架效应。通过分析两种成桥状态下的工况, 得到边、中跨关键位置处的剪力滞系数分布规律。表2表示了关键位置1和3的截面剪力滞系数分布规律, 表3表示了关键位置处截面板件沿桥梁纵向分布规律。

通过表2分析可知, 在自重作用下, 通过对边、中跨关键截面顶底板剪力滞系数分布规律的分析, 可知, 边跨网格加密1区顶板3号、6号板块及底板28号板块为正剪力滞, 顶板9号、底板的34号及31号板块为负剪力滞; 网格加密3区的顶板3号、底板的34号、31号为负剪力滞, 顶板的6号、9号板块及底板的28号板块为正剪力滞。中跨网格加密1区顶板3号板块、底板34号、31号板块为负剪力滞, 顶板6号、9号板块及底板28号板块为正剪力滞; 网格加密3区顶板3号、6号、9号板块均为正剪力滞, 底板的34号、31号、28号板块均为负剪力滞。边、中跨截面上腹板间的顶底板出现了正负剪力滞效应的交替现象, 截面上并没有出现通常箱梁所具有的剪力滞效应分布规律, 也即腹板与顶板交汇处出现正剪力滞, 而远离腹板是负剪力滞, 所以在有斜拉索存在的情况下, 和多箱室的梁桥剪力滞系数分布规律不同, 梁桥的剪力滞系数是按照图1所示规律分布的。在自重作用下, 波形钢腹板斜拉桥边中跨截面剪力滞系数分布不规律。

在自重和预应力作用下, 通过对边、中跨关键截面顶底板剪力滞系数分布规律的分析, 可知, 边跨、中跨网格加密区截面上的剪力滞系数分布规律与自重作用下分布规律几乎一致, 说明预应力对剪力滞系数有规律的分配没有作用。由于斜拉索的作用, 波形钢腹板组合梁桥截面剪力滞系数分布不规律。

通过表3可知, 在自重作用下, 通过对边、中跨顶底板剪力滞系数纵向分布规律的分析, 可知, 边跨顶板正剪力滞系数最大达到1.69, 负剪力滞系数最小达到0.538; 底板剪力滞系数也有正负分配, 正剪力滞系数最大达到3.05, 负剪力滞系数最小达到0.437。中跨顶底板的剪力滞系数小于边跨, 顶板正剪力滞系数最大达到1.47, 负剪力滞系数最小达到0.79; 底板正剪力滞系数最大达到1.34, 负剪力滞系数最小达到0.63。沿桥梁纵向, 边跨端部剪力滞系数波动较大, 中跨顶板中间9号板块的剪力滞系数波动较大, 其他较为均匀, 中跨底板近桥塔部位剪力滞系数波动较大, 趋近于跨中是比较均匀。因此自重作用下, 正剪力滞系数可以取顶底板的最大值的平均值为2.37, 负剪力滞系数取最小值为0.437。

在自重和预应力作用下, 通过对边、中跨顶底板剪力滞系数纵向分布规律的分析, 可知, 边跨和中跨在考虑预应力作用下, 使得剪力滞系数减小, 与纯自重作用时的分布规律几乎一致。边跨顶板正剪力滞系数最大为1.29, 底板负剪力滞系数最小为0.75; 中跨顶板正剪力滞系数最大为1.21, 底板负剪力滞系数最小为0.78。因此自重和预应力作用下, 正剪力滞系数可以取顶底板的最大值的平均值为1.25, 负剪力滞系数取最小值为0.75。

综上所述, 基于设计的角度考虑, 边跨正剪力滞系数最大可取2.37, 负剪力滞系数最小可取0.437; 中跨正剪力滞系数最大可取1.47, 负剪力滞系数最小可取0.75。

表2

Table 2

表2(Table 2)

表2 桥梁关键位置横截面剪力滞系数分布规律 Table 2 Shear lag coefficient distribution over cross section at key longitudinal locations of bridge

表2 桥梁关键位置横截面剪力滞系数分布规律 Table 2 Shear lag coefficient distribution over cross section at key longitudinal locations of bridge

表3

Table 3

表3(Table 3)

表3 关键截面剪力滞系数纵向分布规律 Table 3 Shear lag coefficient distribution in the longitudinal direction

表3 关键截面剪力滞系数纵向分布规律 Table 3 Shear lag coefficient distribution in the longitudinal direction

(1)波形钢腹板斜拉桥建造不多, 多塔斜拉桥更为少见, 设计计算时多采用单梁和实体模型相结合。在采用剪力滞系数考虑截面有效分布宽度时, 主要是仿照混凝土箱梁经验取值、类似工程经验取值或试算取值, 达不到精细化设计的目的。空间网格分析方法可以得到顶底板各个板块所需要的结果, 做到精细化计算分析与设计, 文中所分析的剪力滞系数, 设计时边跨正剪力滞系数最大可取2.37, 负剪力滞系数最小可取0.437; 中跨正剪力滞系数最大可取1.47, 负剪力滞系数最小可取0.75, 可为类似工程设计提供参考。

(2)箱梁的空间网格模型将顶底板划分为各个板块, 可以得到截面完整的应力分布, 因此, 它不存在有效分布宽度的问题。

(3)空间网格模型分析的完整性应用在波纹钢腹板组合箱梁桥的受力分析中, 由于网格模型中各个单元均为梁单元, 各个板块的内力、应力、位移等各种工况下的结果都可以读取出来, 从建模和读取结果的优越性可以看出其优势在于:完全反映截面扭转畸变、以及剪力滞效应。

(4)空间网格模型弥补了单梁模型、平面梁格模型及实体模型的不足, 从分析的完整性、验算应力的全面性来看, 空间网格模型对精细化设计开展了新思路。