劈裂注浆时土体裂缝扩展问题可以看作是浆液在土体中流动与土体变形的动态耦合过程^[12]。在数值模拟计算时, 一般通过耦合求解应力平衡方程式的方式实现^[13], 即首先建立流体连续性方程式, 然后再进行计算。

根据Gothä ll等^[14]的研究, 原状土体中裂隙往往在地应力作用下紧密闭合, 但由于裂隙并非是完全平滑的, 压力仅通过两侧土体间的少数接触部分进行传递。注浆时, 由于浆液承担了土体间的部分压力, 因此通过有效应力原理解决^[15]。非饱和土力学中土的有效应力与孔隙水压力直接相关, 孔隙水压力的产生或变化离不开土的变形^[16], 所以裂缝扩展过程可以看作是有效应力与土体的孔隙比n、渗流速度v_w、渗透率等渗流参数相互影响, 即渗流场与岩土变形场耦合的过程^[17]。

岩石断裂力学导论中提出岩土体变形为线弹性变形^[15], 其假设遵从广义胡克定律, 继而得出其有效应力表示的平衡方程为:

∫V(σ--uwI)δε·δdV=∫VtδvδdS+∫VfδvdV+∫VnρwδvdV(1)

流体连续性方程式:

ddt∫Vρwρw0ndV=-∫Sρwρw0nn-·vwdS（2）

式中:V为积分区域; S为积分区域的表面; δ v为虚速度场; δ 为虚变形率; 为有效应力; t为单位面积表面外力; f为单位体积体力(不包括流体重力); g为重力加速度; ρ _w为流体密度; 为流体参考密度; v_w为渗流速度; n为孔隙率; 为表面的外法线方向; I表示单位矩阵。

在ABAQUS中判断裂纹是否扩展的准则有3种, 即临界应力准则、临界裂纹张开位移准则和裂纹长度对时间准则^[15]。而劈裂注浆过程中裂纹的扩展破坏属于拉伸破裂还是剪切破裂取决于地应力、岩石和流体的各种力学特性, 考虑到土体裂纹的扩展是一个裂纹尖端脆性断裂的过程, 本文选择临界应力作为裂纹扩展准则。

临界应力准则中判断裂纹能否扩展的条件是, 在裂纹扩展期间, 端部各点的应力强度因子等于或者大于黄土临界应力强度因子^[5]。

ABAQUS中临界应力准则为:

f=σ^nσf2+τ^1τ^1f2+τ^2τ^2f2（3）

σ^n=maxσn, 0(4)

式中: σ^n为指定点处的法向应力分量; τ^1和 τ^2为指定点处的剪切应力分量; σ ^f、 τ^1f和 τ^2f分别为临界法向应力和临界剪切应力, 其值由用户指定。在二维问题分析中由于与剪切失效应力不相关, 因此不需要指定此值。

裂缝扩展的断裂准则为^[18]:

KI≥KIC5

式中:K_Ι 为裂纹扩展判据, 即裂纹应力强度因子; K_{Ι C}为断裂韧度。

KΙ=pπEkba12(a2sin2φ+b2cos2φ)146

式中:E(k)为第二类完全椭圆积分, 即:

Ek=∫0π21-k2sin2α)12dα7k2=a2-b2a28

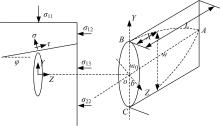
在层状介质二维流场的理论分析中, 一般把劈裂注浆过程浆液在裂缝内的流动假设为液体在两块多孔板间的层流流动, 可按牛顿流体进行分析^[7]。图1为裂缝形态扩展模型。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 裂缝形态扩展模型Fig.1 Extended model of crack shape

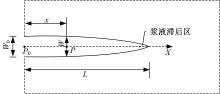
为简化计算, 模型分析时假设劈裂注浆过程中裂缝高度保持不变, 故将裂缝内二维流动简化为一维流动^[7], 图2为裂纹扩展平面模型。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 裂纹扩展平面模型Fig.2 Planar model of crack growth

扩展方程满足^[19]:

dpdx=12μqhfw3(9)

式中:μ 为浆液黏性系数; w为裂缝宽度; q为沿裂缝扩展方向单位长度上的体积流量; h_f为裂缝的高度。

w=w01-x2/L210

将式(10)代入式(9)积分得:

p=-12μqLxhfw03L2-x2+C011

由边界条件:

p|x=0=P012

可求得:

C0=P013

裂缝面上的压力分布可表示为:

p=-12μqLxhfw03L2-x2+P014

式(14)中各个不同点处的裂缝宽度都用w₀表示, 将式(10)代入式(14), 化简得到:

p=-12μqxhfw02w+P015

当x→ L时, 亦即w→ 0时, 由式(15)可知p→ -¥ , 可见式(15)存在解的奇异性, 这显然不符合实际情况, 这一区域称为流体滞后区^[19]。为了避免方程奇异性所导致的压力不合理, 进一步假设流体滞后区内的流体压力应不小于周围岩土渗流场边界上的压力, 因此裂缝扩展方程可写成如下形式:

p=-12μqxhfw02w+P0, p< P^P^, p≥P^(16)

式中:为根据渗流方程计算估计求得的渗透压力。

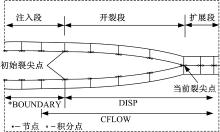
劈裂注浆裂纹扩展过程中裂缝长度和裂缝宽度是随着浆液注入条件实时动态变化的, 但ABAQUS中自带的CFLOW无法实现对特定单元进行流动赋值, 本文借助ABAQUS软件提供的CFLOW子程序接口进行注入赋值曲线的编写, 同时根据子程序DISP加载, 通过式(16)实时计算裂缝扩展过程中浆液压力沿裂缝分布的功能。图3为裂纹扩展有限元分析模型示意图。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 裂纹扩展有限元分析模型示意图Fig.3 Schematic diagran of finite element analysis model of crack growth

裂缝扩展方程的表达式虽然简单, 但具体实现却很困难。本文将任意时刻的裂缝扩展分成3段(如图3所示):注入段、开裂段和扩展段。进行有限元计算时, 首先通过子程序CFLOW计算压力值P₀, 按如图3所示的方式设定边界CFLOW, 通过指令^* BOUNDARY将压力值P₀实时动态地传递给子程序DISP。然后, 再通过子程序DISP计算裂缝内每个节点的坐标值, 就可以求得裂缝面内每一对节点的相对距离, 这个相对距离即为裂缝扩展段该处的宽度w。

在计算裂缝面内各个节点的压力值时, 子程序DISP通过压力值P₀和宽度w就可以根据裂缝扩展方程式(16)计算得出不同节点的压力值变化情况。

浆液注浆过程模拟时, 调用ABAQUS中inp文件, 通过在CFLOW命令中添加注入幅值曲线, 获得施加注入条件。

应用有限元模拟软件ABAQUS对劈裂注浆过程裂缝扩展进行计算时, 由于预设裂缝跟地应力存在夹角, 所以采用xfem进行建模计算。模型区域如图4所示, 图5为有限元网格划分预设裂缝局部图。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 有限元计算模型Fig.4 Finite element calculation model

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 有限元网格划分预设裂缝局部图Fig.5 Local image of presetting crack with finite element mesh dividing

土体介质按均质各向同性弹性材料考虑, 采用最大主应力破坏准则MAXS, 联结单元采用COHZD4单元, 其他土体均采用四节点双线性平面应力四边形单元(CPS4R)。

参数选取如下:黄土泊松比为0.3, 黏聚力为32 kPa, 水泥浆液黏度液体黏度系数为5× 10^-6 Pa· s, 由于湿陷性黄土孔隙的存在, 使得浆液在土中流动过程会发生滤失现象, 故规定裂缝滤失系数为5× 10^-10。Cohesive单元选用COH2D4单元, 其他材料选用CPS4R单元。

2.3.1 浆液-土体的耦合效应

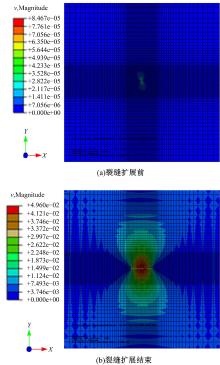
通过对不同时间位移云图的变化情况来分析单元的损伤情况, 可以得出在不同时间段的裂缝扩展情况。图6为裂缝扩展前和扩展结束时位移场分布图。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 裂缝扩展前和扩展结束时位移场分布图Fig.6 Displacement field distribution before and crack growth finished

通过对不同时间段的压力分析发现, 单元的破坏随着时间的推移慢慢向上推进, 失效单元慢慢增加。同时裂缝的扩展也随失效单元的增加而慢慢向外扩展, 说明此时裂缝内应力强度大于单元的应力强度因子。随着裂缝的扩展, 裂缝内应力强度慢慢变小直至小于单元的应力强度因子, 此时裂缝扩展结束。

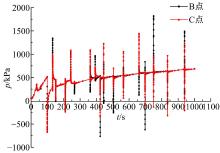
为研究裂尖应力变化情况, 取A点单元绘制其压力随时间变化曲线, 如图7所示。当裂纹尖端应力P₀小于150 kPa时, 单元裂尖法向应力随时间变化缓慢增加, 随着裂纹的持续扩展, 在80 s左右, 其单元点应力突然增大至150 kPa, 然后又瞬间回落, 说明此时单元破坏, 裂缝扩展开始。此时的注浆压力为土体劈裂注浆时的起裂压力, 在裂纹起裂后, 应力集中能快速释放, 应力也随之降低, 随着注浆的继续, 裂纹尖端前移, 使得A点的孔隙压力表现为循环集中释放过程, 且整体表现为上升趋势。若不考虑土体的破坏状态, 随着裂纹的不断前进扩展, 所需的压力持续增加。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 A点单元位置及其压力随时间的变化图Fig.7 Diagram of pressure at element of point A changing with time

选取注浆孔上、下两个单元绘制其注浆过程压力变化曲线, 如图8所示。由图可见, 注浆孔处的压力并不是直线上升的, 裂缝上、下两个单元的压力变化趋势基本相同。从图中还可以看出, 起裂时的孔隙压力在500 kPa左右, 而后期出现逐渐增大现象。说明压力在裂缝扩展中存在一个能量聚集过程, 当能量聚集到一定程度后, 才能促使土体裂缝继续扩展。在黄土劈裂注浆过程随着浆液扩散范围也增加, 浆液在地层中受到的阻力增加, 因注浆过程中需要维持注浆流量恒定, 要保持注浆孔压力增大, 所以图中出现压力上下波动的情况, 但浆液压力不断增加, 也伴随着土体受力面积不断增大, 因此在同一位置隙宽增量随时间不断增大, 但增长趋势随时间逐渐减缓。如图9所示, 裂缝宽度增量随时间流逝逐渐衰减。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 注浆口压力随时间变化图Fig.8 Diagram of pressure at grouting hole changing with time

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 裂缝宽度随时间变化图Fig.9 Diagram of crack width changing with time

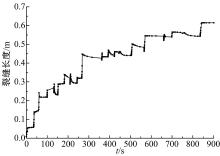
图10显示了裂缝长度随时间的变化曲线。从图中可以看出, 裂缝长度随时间的变化并不是光滑的直线, 而是在每一个时间段会出现一个稳定状态, 说明裂缝扩展过程并不是一次完成的, 而是随着压力的增加,

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 裂缝长度随时间变化图Fig.10 Diagram of crack length changing with time

裂缝尖端压力慢慢达到黄土的断裂压力, 此时, 裂缝内应力强度大于土体的应力强度, 继而发生扩展现象。

通过以上分析可以看出, 浆液-土体的耦合效应受浆液压力、裂缝宽度和裂缝长度影响明显。而浆液压力对隙宽增量影响更为显著, 而隙宽的增加又可促使浆液获得更远的扩散距离。因而, 在黄土劈裂注浆过程中选择合适的时间增加压力可更为有效地增强浆液扩散能力。同时, 水泥浆液作为颗粒型浆液, 其可注性是实际注浆工程中所关心的重要问题。由于黄土一般为微小裂隙, 滤失效应明显, 若压力不够, 可能导致水泥颗粒不断淤积, 使浆液的扩散能力降低。而提高注浆压力可使浆液运移锋面处的隙宽明显增大, 从而提高浆液的可注性, 降低滤失效应的影响。但由于湿陷性黄土特殊的结构性使得其注浆压力又不宜过大, 过大可能导致土体坍塌。综合以上分析可知, 实际工程对黄土进行注浆时, 在适当的时间提高注浆压力可以明显增大浆液在裂隙中的扩散距离, 从而对土体加固起到更为有效的目的。

2.3.2 裂缝扩展的影响因素

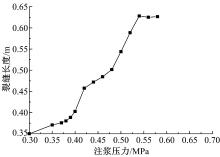
劈裂注浆中通过浆液的压力促使土体裂缝扩展, 使土体原有结构发生改变, 通过浆液的填充消除土体的架空空隙, 进而消除土体的湿陷性, 达到加固的目的^[20]。注浆压力与裂纹扩展距离的关系如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 裂缝长度随注浆压力变化曲线Fig.11 Curve of crack length changing with grouting pressure

从图11中可以看出, 裂纹长度在注浆前期受注浆压力的影响显著; 随着裂纹长度的增大, 注浆压力呈现非线性增大趋势, 最后趋于稳定, 裂纹长度不再变化。同时, 裂纹长度的非线性扩展说明本地黄土结构完整性较好, 因为只有完整性较好的黄土土体才能形成较长的裂纹长度, 反之, 若裂纹长度随注浆压力的增大变化不甚明显, 则说明本地黄土土体结构不完整, 可能存在破损^[21]。同时, 随着裂纹长度的增大, 浆液在土体中的扩展过程需要克服的张拉应力和剪切应力也随之增大^[22], 所以, 图11中显示随着裂纹长度的增加, 注浆压力随之增大。

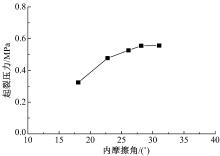
劈裂注浆裂缝的扩展不仅与注浆施工工艺有关, 而且与地应力、土体物理力学性质有关。内摩擦角作为岩(土)体的两个重要参数之一, 是土的抗剪强度指标, 是工程设计的重要参数^[23]。土的内摩擦角反映了土的摩擦特性, 劈裂注浆时裂缝内浆液的流动受土的内摩擦角影响显著。图12为注浆压力随内摩擦角的变化曲线。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 注浆压力随内摩擦角的变化曲线Fig.12 Curve of grouting pressure changing with angle of internal friction

根据文献[20]可知, 岩土材料的抗剪强度有凝聚力和内摩擦力两部分, 但是凝聚力在变形不大时就达到峰值, 而摩擦力却是在发生相当大的变形后才能充分发挥, 所以凝聚力显示的是岩土的脆性性质, 而内摩擦力显示的是塑性性质。从图12可以看出, 随着土体内摩擦角的增大, 所需要的注浆起裂压力逐渐增大。因为岩土的破坏过程正是摩擦力逐步发挥作用的过程, 所以土体内摩擦角越大, 注浆压力要克服土体强度而使浆液流动的阻力也就越大, 因而需要的注浆压力就越大。但当起裂压力为0.55 MPa左右时, 起裂压力随内摩擦角的增加不再增大。

试验设备主要包括模拟槽、注浆系统及数据采集系统3大部分。

模拟槽由钢化玻璃、注浆管、可调节钢板组成; 注浆系统由气缸、稳压罐、油泵、高压管和丝杠系统组成。数据采集系统采用飞科新技术公司研制的灌浆自动记录仪GMS2006, 自动记录仪由注浆压力测定装置、数据传输线、数据接收仪及操作软件构成, 可以对注浆压力进行实时监测并采集。

试验模拟装置的结构示意图如图13所示。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 模型装置图Fig.13 Diagram of model device

(1)填充材料

兰州新区某快速道路工程K1+662.053段工程, 地层自上而下为:黄土、砂砾层和基岩。充填材料选用取现场土样进行模型试验, 原状黄土的力学性能如下:含水率ω 为20.3%, 孔隙比e为1.10, 弹性模量E为20 MPa, 泊松比μ 为0.3, 黏聚力c为32 kPa, 内摩擦角φ 为26° 。

(2)注浆与记录系统

试验采用HJB型活塞式灰浆注浆泵, 使用空气压缩机提供动力, 如图14所示。

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 注浆装置图Fig.14 Diagram of grouting device

注浆材料选用水泥单液浆, 采用祁连山牌PO.42.5普通硅酸盐水泥与水混合而成, 水灰比为1∶ 1, 参数与模型参数相同。

实际试验过程中劈裂注浆土体裂缝扩展可以以土体位移量的变化情况来分析^[21]。由于测区内裂缝扩展形式比较复杂, 难以进行判断统计, 因此本文通过对模型箱拆解, 然后进行剖面, 测量浆液在土体中的扩展情况(见表1)。图15为选取了3组不同压力下的浆液扩散情况。

表1

Table 1

表1(Table 1)

表1 裂缝扩展测试结果 Table 1 Test results of crack propagation 编号 注浆压力 /MPa 裂缝长度 /m 上延高度 /m 下延高度 /m 1 0.5 0.45 0.031 0.029 2 0.5 0.43 0.027 0.025 3 0.5 0.45 0.030 0.026 4 0.35 0.22 0.022 0.021 5 0.35 0.22 0.022 0.025 6 0.35 0.23 0.021 0.020

表1 裂缝扩展测试结果 Table 1 Test results of crack propagation

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 不同注浆压力下的浆液扩散情况Fig.15 Grout diffusion with different grouting pressure

根据测试1~6试验土体的剖面资料(见表1), 劈裂后裂缝扩展在0.22~0.45 m。通过对比图6(b), 其不同压力下的土体裂缝扩展模拟结果与试验的数据基本一致。同时发现, 在低压力下扩散距离较小, 但在注浆管附近, 土体位移量较大。因此可以推断, 在低压力下浆液会长时间处于鼓泡形式, 对土体进行挤密, 高压力下土体以劈裂为主, 浆液流动较远(见图15(b))。同时, 断裂面总体呈现出一直沿着劈裂面向下劈裂趋势, 很少可能出现二次劈裂^[24]。但当压力一次性达到1.3 MPa时, 浆液会沿注浆管出现冒浆现象(见图15(c)), 所以, 试验过程中对注浆压力进行分段控制, 此过程说明黄土劈裂注浆过程存在一定的能量损失, 与传统意义上的直接增大压力注浆存在明显区别。说明在黄土劈裂注浆过程中无法通过连续加压进行劈裂注浆, 应分段加压, 确保扩展过程中能量的聚集。

表1中土体裂缝扩展长度与延度比值和土体应力状态密切相关, 其比值与土体测量圆内大小主应力比值呈线性关系, 这也验证了劈裂裂缝在最小的主应力面方向进行扩展的结论。

在浆液压力作用下, 裂隙面会向外产生一定位移, 同时裂缝在平面上产生延展, 即隙宽增量。对比图6(b)可见, 在注浆孔处位移最大, 且沿浆液扩散方向迅速衰减, 除注浆孔以及浆液运移锋面附近, 衰减随扩散距离近似呈线性关系。在远离注浆孔处出现隙宽衰减现象。从图中可以看出, 浆液运移锋面处的隙宽增量大于0, 即土体受浆液影响范围大于浆液扩散范围。

试验发现, 土体的工程力学特性非常复杂并且具有区域性, 而土体的特性是进行注浆加固设计的基础。为研究浆液在土体中扩散的影响因素, 取试验土样并利用中国科学院近代物理研究所JSM-5600LV低真空扫描电子显微镜进行室内微结构电镜试验, 黄土土样微观结构见图16。

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 原状黄土在SEM下的微观结构图Fig.16 Microstructure of undisturbed loess by SEM

微观结构分析发现, 土体结构空隙分布存在差异, 导致劈裂面具有不确定性导, 使得每次注浆时浆液走向不同, 造成周围土体裂缝扩展在局部存在离散性^[25]。这也正说明了土体颗粒的胶结具有结构性, 裂缝的扩展正是胶结较弱的薄弱带断裂造成的。试验与模拟都显示:一定注浆压力下, 土体地应力及内摩擦力等参数对土体注浆后的宏观力学行为有比较明显的影响, 这与注浆试验是吻合的。