工作平台可翻转的3D打印机装置结构分析

引用本文

曲兴田, 闫龙威, 孙慧超, 周伟, 李光辉. 工作平台可翻转的3D打印机装置结构分析. 吉林大学学报（工学版）, 2017, 47(5): 1489-1497
QU Xing-tian, YAN Long-wei, SUN Hui-chao, ZHOU Wei, LI Guang-hui. Structure analysis of 3D printer device of reversible working platform. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1489-1497 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705021
Permissions

工作平台可翻转的3D打印机装置结构分析

曲兴田, 闫龙威, 孙慧超, 周伟, 李光辉

吉林大学机械科学与工程学院,长春 130022

通信作者:孙慧超(1981-),男,工程师.研究方向:3D打印和机械产品创新设计.E-mail:sunhc@jlu.edu.cn

作者简介:曲兴田(1962-),男,教授.研究方向:先进制造技术.E-mail:quxt@jlu.edu.cn

基金项目:国家自然科学基金项目(51135006,51505185)

摘要

为了解决当前3D打印制造过程中一些具有悬臂或者空腔结构又不允许添加内部支撑结构的打印件无法制造的问题,设计出一种工作平台可翻转的3D打印机,介绍了其结构组成以及工作原理;通过对系统模型进行运动学分析,得到工作平台机构运动学正解与逆解,为结构的速度分析和运动控制等研究提供了基础。利用ANSYS仿真软件对系统建立仿真模型,得到工作平台结构和喷头结构的应力与模态分析,验证了设计方案的可行性。实现了工作平台可翻转的可能性,完成无支撑结构的曲面结构打印。

关键词: 机械设计; 3D打印; 结构分析; 空间轨迹规划; 模型仿真

中图分类号:TH161 文献标志码:A 文章编号:1671-5497(2017)05-1489-09

Structure analysis of 3D printer device of reversible working platform

QU Xing-tian, YAN Long-wei, SUN Hui-chao, ZHOU Wei, LI Guang-hui

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

In order to solve the current problem that some printed pieces with cantilever and cavity structures but not allowed to add internal support can not be printed, a type of 3D printer with reversible working platform was designed. The structure composition and working principle were introduced. Through kinematic analysis of the system model, the kinematic positive and inverse solutions of the working platform mechanism were obtained, which provide the basis for the velocity analysis and motion control of the 3D printer mechanism. The simulation model was established using ANSYS simulation software, the stress and modal analysis of the structure of the working platform and the nozzle were obtained, which verify the feasibility of the design scheme. Consequently, the possibility that the working platform can be turned over was achieved and the non-support surface structure can be printed.

Key words: mechanical design; 3D printing; structure analysis; space trajectory planning; model simulation

Show Figures

0 引言

3D打印制造就是将三维模型分解成二维层状结构, 逐层累加制造。由于3D打印在制造复杂模型不增加成本、制造材料无限制组合以及可以进行精确的实体复制等优势, 使其快速成为企业研发的主要对象以及大众关注的热点。并且在一体化加工和多材料同步一体化加工方面, 3D打印有着其特有的优势。目前, 这一直接制造技术在国内外已经成功应用于航空航天、医疗等领域, 推动了先进制造技术的进步, 提升了先进制造技术的水平^{[1, 2, 3]}。

对于3D打印结构模型, 科学、合理、经济的结构一直是研究人员所追求的。目前, 3D打印机打印大角度曲面以及中空和悬臂结构时, 受到重力因素影响, 需要添加光敏树脂或特殊材料作支撑处理。由于当前3D打印机对不同结构填充支撑材料方式与填充材料相同, 从而存在强度问题^{[4, 5]}、耗材问题^[6]、稳定性问题等^[7], 并且一些不允许添加支撑材料的结构就无法进行3D打印。本文设计了一种工作平台可翻转的3D打印机, 可以通过工作平台翻转减少甚至取消支撑结构, 从而在材料节约方面结构优化, 可以解决当前3D打印制造过程中一些具有悬臂或者空腔结构又不允许添加内部支撑结构的打印件无法制造的问题。该打印机在成型速度、可成型材料种类、设备价格、运行和维护成本等方面具有明显优势, 具有良好的发展潜力和广阔的应用前景, 代表着快速成型技术的发展方向。

1 系统的结构组成和工作原理

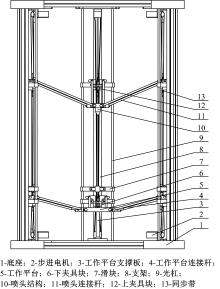
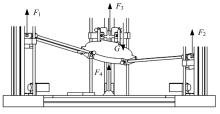
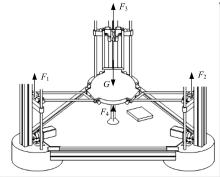
少自由度并联机构由于具有高刚度、高精度、构造简单、制造和控制相对容易, 且便于连接其他机构的优越性, 因而广泛应用于独立机构、关节机构、机床工作台、工件定位、微动机构等领域^[8]。并联机构是由两个或两个以上的运动链将固定平台和运动平台连接在一起, 驱动装置至少分布在两个或两个以上的分支运动链上, 而且一般具有两个或两个以上的自由度^[9]。一种工作平台可翻转的3D打印机装置结构如图1所示。这种工作平台可翻转的3D打印机的核心机构包括3-SPS工作平台并联机构和3-SPS喷头并联机构。3-SPS工作平台并联机构由动平台、工作平台连接杆和下夹具块组成, 能够实现3D打印过程中打印平台沿轴倾斜, 这里的3-SPS是指工作平台连接杆与工作平台之间为球铰副S, 下夹具滑块为移动副P, 工作平台连接杆与下夹具块之间为球铰副S; 3-SPS喷头并联机构由喷头组件、上夹具块、滑块和支撑杆组成, 实现3D打印过程中喷头结构3个方向的平动, 这里的3-SPS是指喷头与支撑杆之间为球铰副S, 上夹具块在光杠上滑动为移动副P, 上夹具块与连接杆之间为球铰副S。

	Figure Option View Download New Window
	图1 工作平台可翻转的3D打印机装置Fig.1 3D printer device of reversible working platform

工作平台轴倾斜的工作流程如下:

(1)步进电机旋转带动相应的同步带旋转。

(2)同步带绕在下夹具块上, 同时下夹具块固定在滑块上, 而滑块套在光杠上, 这样同步带旋转带动了下夹具块的直线往复运动。

(3)工作平台连接杆一端连接在下夹具块上, 一端通过球铰链连接在运动平台上, 这样, 单边连接杆的运动使工作平台移动。

(4)工作平台与底座通过一根支撑杆连接, 而支撑杆与工作平台则用虎克铰相连, 可将连接杆的运动转变为工作平台的轴倾斜。

喷头结构3个方向的运动流程如下:

(1)步进电机旋转带动同步带旋转。

(2)同步带绕在上夹具块上, 与工作平台类似, 将皮带的旋转运动转变成了上夹具块的直线往复运动。

(3)上夹具块再带动连接在喷头上的连接杆运动, 最终实现喷头的3个方向平动。

2 结构空间运动分析

2.1 工作平台运动学逆解

运动学逆解就是通过机构平台的位姿, 求解机构输入主动副的位移。对于具有曲面加工特性的3D打印机结构的喷头机构逆解就是通过已知的喷头位置求解结构主动副上夹具滑块的输入位置。求解运动学逆解就是给定动平台在定坐标系下的坐标, 求解静坐标系下3个主动副的位移量^[10]。

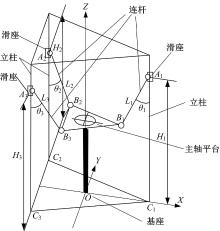
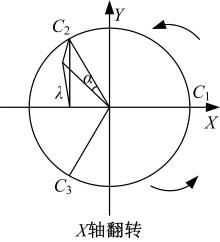
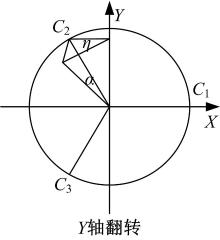
本文具有曲面加工特性的3D打印机的工作平台主要的运动为X轴转动和Y轴转动, 所以当求解其逆解时将其分开讨论。如图2所示, 由机构原理可将X轴转动分解为C₁滑块固定不动, C₃和C₂滑块运动将工作平台沿X轴翻转。将Y轴转动分解为C₁和C₂滑块将工作平台沿Y轴翻转。C₃为随动, 其运动轨迹与C₂相同。由于工作平台3-SPS并联机构移动副限制以及工作平台Z轴旋转限制, 工作平台与工作平台连接杆铰点B₁、B₂、B₃只能在平面y=0、y=- $\begin{matrix} \sqrt[]{3} \end{matrix}$ x内运动。

	Figure Option View Download New Window
	图2 工作平面运动分析Fig.2 Kinematic analysis of working plane

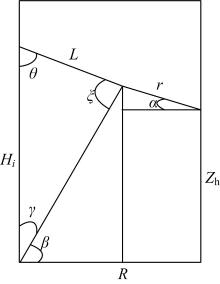
如图3所示, 将其中一个平面展开, 工作平台距离底座高度为Z, 工作平台连杆长度固定为L, 机构底座外接圆半径为R, 工作平台外接圆半径为r, 在其平面内工作平台倾斜角为α , 主动副滑块输入量为H_i。

	Figure Option View Download New Window
	图3 工作平面Fig.3 Working plane

由三角形正弦定理可知:

$\begin{matrix} \frac{\sqrt[]{{(R - rcosα)}^{2} + (Z_{h} {+ rsinα)}^{2}}}{sinθ} \end{matrix}$ = $\begin{matrix} \frac{L}{sinγ} \end{matrix}$ = $\begin{matrix} \frac{H_{i}}{sinξ} \end{matrix}$ sinγ =sin $\begin{matrix} (\frac{π}{2} - β) \end{matrix}$ =cosβ =

$\begin{matrix} \frac{R - rcosα}{\sqrt[]{{(R - rcosα)}^{2} + (Z_{h} {+ rsinα)}^{2}}} \end{matrix}$

sinθ = $\begin{matrix} \frac{\sqrt[]{{(R - rcosα)}^{2} + (Z_{h} {+ rsinα)}^{2}}}{L} \end{matrix}$ sinγ = $\begin{matrix} \frac{R - rcosα}{L} \end{matrix}$

H_i= $\begin{matrix} \frac{sinξ}{sinγ} \end{matrix}$ L= $\begin{matrix} \frac{\sin (π - θ - γ)}{sinγ} \end{matrix}$ L= $\begin{matrix} \sqrt[]{L^{2} - {(R - rcosα)}^{2}} \end{matrix}$ +Z_h+rsinα

将y= $\begin{matrix} \sqrt[]{3} \end{matrix}$ x平面中工作平台的翻转角度反推成X轴工作平台的翻转角度, 如图4所示, y= $\begin{matrix} \sqrt[]{3} \end{matrix}$ x中工作平台翻转角度为α , 工作平台在X轴翻转角度为λ 。

	Figure Option View Download New Window
	图4 X轴翻转Fig.4 X-axis rotation

sinλ = $\begin{matrix} \frac{Rsinα}{Rsin 60 °} \end{matrix}$ = $\begin{matrix} \frac{2 \sqrt[]{3}}{3} \end{matrix}$ sinα , 则sinα = $\begin{matrix} \frac{\sqrt[]{3}}{2} \end{matrix}$ sinλ ,

cosα = $\begin{matrix} \sqrt[]{1 - si n^{2} α} \end{matrix}$ = $\begin{matrix} \sqrt[]{1 - \frac{3}{4} si n^{2} λ} \end{matrix}$ = $\begin{matrix} \frac{\sqrt[]{4 - 3 si n^{2} λ}}{2} \end{matrix}$

将其代入:

$\begin{matrix} H_{i} = \frac{sinξ}{sinγ} L = \frac{\sin (π - θ - γ)}{sinγ} L = \sqrt[]{L^{2} - {(R - rcosα)}^{2}} + Z_{h} + rsinα \end{matrix}$

即得到工作平台并联机构X轴翻转逆解:

$\begin{matrix} H_{i} = \sqrt[]{L^{2} - {(R - \frac{r \sqrt[]{4 - 3 si n^{2} λ}}{2})}^{2}} + Z_{h} + \frac{r \sqrt[]{3} sinλ}{2} \end{matrix}$

再将y= $\begin{matrix} \sqrt[]{3} \end{matrix}$ x平面中工作平台的翻转角度反推成Y轴工作平台的翻转角度, 如图5所示, y= $\begin{matrix} \sqrt[]{3} \end{matrix}$ x中工作平台翻转角度为α , 工作平台在Y轴翻转角度为η 。得到工作平台并联机构X轴翻转逆解为:

$\begin{matrix} H_{i} = \sqrt[]{L^{2} - {(R - \frac{r \sqrt[]{4 - 3 si n^{2} η}}{2})}^{2}} + Z_{h} + \frac{rsinη}{2} \end{matrix}$

	Figure Option View Download New Window
	图5 Y轴翻转Fig.5 Y-axis rotation

2.2 工作平台并联机构运动学正解

运动学正解就是机构输入移动副的位移, 求解机构动平台的位姿。求解运动学正解就是给定静坐标系下3个主动副的位移量求解动平台在定坐标系下的坐标^[11]。对于具有曲面加工特性的3D打印机结构的工作平台并联机构正解就是通过已知的下夹具块的输入位置求解工作平台倾斜角度。求解运动学正解就是给定静坐标系下3个主动副的位移量求解动平台在定坐标系下倾斜角度。当工作平台沿X轴翻转时, 下夹具滑块C₁固定, 工作平台通过下夹具滑块C₂、C₃进行翻转。

如图2所示建立机构的静坐标系, 设工作平台支撑杆与光杠间夹角为θ _i, 下夹具块的输入为H_i, 工作平台中心距离底座为Z_h, 则工作平台与工作平台支撑杆交点处在静坐标系下的坐标为:

B₁(R, 0, Z_h),

B₂ $\begin{matrix} (\frac{Lsin θ_{2} - R}{2}, \frac{\sqrt[]{3} (R - Lsin θ_{2})}{2}, H_{2} - Lcos θ_{2}) \end{matrix}$ ,

B₃ $\begin{matrix} (\frac{Lsin θ_{3} - R}{2}, \frac{\sqrt[]{3} (R - Lsin θ_{2})}{2}, H_{3} - Lcos θ_{2}) \end{matrix}$

由于主动副下夹具块C₂、C₃关于X轴对称, 则在翻转过程中:

$\begin{matrix} \{\begin{matrix} x_{2} = x_{3} \\ y_{2} = - y_{3} \\ z_{2} + z_{3} = 2 Z_{h} \end{matrix} \Rightarrow \{\begin{matrix} θ_{2} = θ_{3} = θ \\ cosθ = \frac{H_{2} + H_{3} - 2 Z_{h}}{2 L} \end{matrix} \end{matrix}$

在静坐标系下, 当工作平台沿X轴旋转λ 角度时工作平台与工作平台支撑杆交点又可以表示为:

$\begin{matrix} \begin{matrix} B'_{1} (r, O, Z_{h}), \\ B'_{2} (\frac{r}{2}, \frac{\sqrt[]{3} rcosλ}{2}, \frac{\sqrt[]{3} rsinλ}{2} + Z_{h}) \\ B'_{3} (\frac{r}{2}, \frac{\sqrt[]{3} rcosλ}{2}, Z_{h} \frac{\sqrt[]{3} rsinλ}{2}) \end{matrix} \end{matrix}$

则工作平台支撑杆与光杠的夹角θ 与工作平台沿X轴翻转的角度λ 间的关系为:

$\begin{matrix} \begin{matrix} \frac{\sqrt[]{3} (R - Lsinθ)}{2} = \frac{\sqrt[]{3} rcosλ}{2} \Rightarrow \\ cosλ = \frac{R - Lsinθ}{r} = \frac{R - L \sqrt[]{1 - co s^{2} θ}}{r} \end{matrix} \end{matrix}$

可得到X轴翻转正解为:

$\begin{matrix} cosλ = \frac{R - Lsinθ}{r} = \frac{R - L \sqrt[]{1 - co s^{2} θ}}{r} = \frac{R - L \sqrt[]{1 - \frac{(H_{2} + H_{3} - 2 Z_{h})^{2}}{4 L^{2}}}}{r} \end{matrix}$

当工作平台沿Y轴翻转时, 下夹具块C₁、C₂、C₃为主动副将工作平台沿Y轴翻转。由于工作平面关于Y轴对称, 且C₂和C₃也关于Y轴对称, 所以C₂、C₃运动相同。在上述坐标系中, 工作平台与工作平台支撑杆交点处的坐标为:

B₁(R-Lsinθ ₁, 0, H₁-Lcosθ ₁),

B₂ $\begin{matrix} (\frac{Lsin θ_{2} - R}{2}, \frac{\sqrt[]{3} (R - Lsin θ_{2})}{2}, H_{2} - Lcos θ_{2}) \end{matrix}$ ,

B₃ $\begin{matrix} (\frac{Lsin θ_{3} - R}{2}, \frac{\sqrt[]{3}}{2} (R - Lsin θ_{2}), H_{3} - Lcos θ_{2}) \end{matrix}$

由于主动副下夹具块C₂、C₃关于X轴对称, 则在翻转过程中:

$\begin{matrix} \{\begin{matrix} x_{2} = x_{3} \\ y_{2} = - y_{3} \\ z_{2} = z_{3} \end{matrix} \Rightarrow \{\begin{matrix} θ_{2} = θ_{3} \\ H_{2} = H_{3} \end{matrix} \end{matrix}$

在静坐标系下, 当工作平台沿X轴旋转η 角度时工作平台与工作平台支撑杆交点又可以表示为:

$\begin{matrix} \begin{matrix} B'_{1} (rcosη, O, Z_{h} - rsinη), \\ B'_{2} (- \frac{r}{2} cosη, \frac{\sqrt[]{3} r}{2}, \frac{rsinη}{2} + Z_{h}), \\ B'_{3} (- \frac{r}{2} cosη, - \frac{\sqrt[]{3} r}{2}, Z_{h} + \frac{rsinη}{2}) \end{matrix} \end{matrix}$

由于工作平台沿Y轴翻转, 则B'₁、B'₂、B'₃到Y轴距离固定, 由模型可知:

$\begin{matrix} \begin{matrix} | X'_{1} | = | 2 X'_{2} | = | 2 X'_{3} |\Rightarrow \\ | R - Lsin θ_{1} | = 2 |\frac{Lsin θ_{2} - R}{2}| \end{matrix} \end{matrix}$

工作平台并联机构中工作平台连接杆与光杠之间夹角为锐角, 则θ ₁=θ ₂=θ ₃。

$\begin{matrix} H_{1} - Lcos θ_{1} + 2 (H_{2} - Lcos θ_{2}) = 3 Z_{h} \Rightarrow cosθ = \frac{H_{1} + 2 H_{2} - 3 Z_{h}}{3} \end{matrix}$

工作平台支撑杆与光杠的夹角θ 与工作平台沿Y轴翻转的角度η 的关系为:

$\begin{matrix} R - Lsinθ = rcosη \Rightarrow cosη = \frac{R - L \sqrt[]{1 - co s^{2} θ}}{r} \end{matrix}$

可得到Y轴翻转正解为:

$\begin{matrix} cosη = \frac{R - L \sqrt[]{1 - co s^{2} θ}}{r} = \frac{R - L \sqrt[]{1 - {(\frac{H_{1} + 2 H_{2} - 3 Z_{h}}{3 L})}^{2}}}{r} \end{matrix}$

3 整体结构应力分析

对并联机构进行静应力分析来确定驱动力经并联机构关节后并联机构的传递效果, 它是运动学分析的延续和动力学分析、刚度分析的基础, 为并联机构的结构尺寸参数设计和动力选择提供理论依据^[12]。

3.1 工作平台沿X轴翻转时结构应力分析

具有曲面加工特性的3D打印机在进行曲面打印时, 工作平台按打印需要进行倾斜翻转。其翻转主要分为沿X轴翻转和沿Y轴翻转。当工作平台沿X轴翻转时, C₁滑块固定不动, C₂、C₃滑块通过步进电机和同步带在光杠上运动。工作平台受力如图6所示。并联机构滑块受到同步带垂直向上的力F₁、F₂、F₃, 工作平台上受到已完成的打印件的重力G, 工作平台支撑杆对工作平台有垂直向上的支撑力。

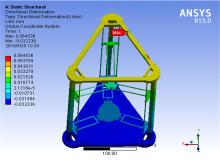
	Figure Option View Download New Window
	图6 工作平台沿X轴翻转受力图Fig.6 Force diagram of working platform along X-axis rotating

将结构进行有限元仿真, 其中具有曲面加工特性的3D打印机材料选为碳素钢Q235AF。其弹性模量为190~210 GPa, 泊松比取0.3, 密度为7.85 g/cm³。由于工作平台与喷头结构等效简化后造型简单, 因此可以选用Mechanical, 自动划分网格。得出工作平台X轴翻转30° 位置打印最大高度时X、Y、Z三个方向的位移, 如图7、图8、图9所示。

从图7中可以看到, 满载静止时X方向上位移分为上、下两部分:结构上部分X方向位移较大(0.04 mm左右), 且有最大位移点在上三角框上为0.06 mm; 下三角框X方向位移较小可忽略, 立柱上X方向位移是从下到上逐渐变大的。从图8中可以清楚看到满载静止时Y方向上位移分为上、下两部分:结构下部分Y方向位移较大(0.05 mm左右), 且有最大位移点在上三角框上为0.055 mm; 上三角框Y方向位移较小可忽略, 立柱上Y方向位移是从下到上逐渐变小的。从图9中可以清楚地看到, 满载静止时Z方向上位移分为两部分:下降滑块立柱一侧Z方向的位移较大且较为平均, 位移都在0.1左右, 而上升和固定滑块两侧立柱的Z方向位移较小(0.06左右)。整体在Z方向的位移是从滑块下降一端逐渐向上升滑块和固定滑块两端下降。整体3个方向的位移较为稳定。

	Figure Option View Download New Window
	图7 X方向位移Fig.7 Displacement in X direction

	Figure Option View Download New Window
	图8 Y方向位移Fig.8 Displacement in Y direction

	Figure Option View Download New Window
	图9 Z方向位移Fig.9 Displacement in Z direction

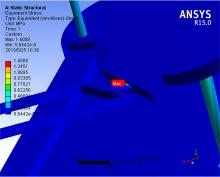
当工作平台X轴翻转时打印最大高度为120.8 mm, 打印材料PLA密度为1.05 g/cm³, 则打印件最大重力为G=π × 40²× 120.8÷ 1000÷ 1000× 9.8=6.24 N。当前市面上喷头结构质量多为350 g, 即3.43 N。在ANSYS当中在工作平台上加载6.24 N垂直向下的力, 在喷头结构上加载3.43 N垂直向下的力, 得到应力分图, 如图10~图13所示。

	Figure Option View Download New Window
	图10 X轴翻转整体应力图Fig.10 Overall stress diagram of X-axis rotation

	Figure Option View Download New Window
	图11 X轴翻转并联杆工作平台应力图Fig.11 Parallel working platform stress diagram of X-axis rotation

	Figure Option View Download New Window
	图12 X轴翻转工作平台连杆应力分析Fig.12 Working platform links stress analysis of X-axis rotation

	Figure Option View Download New Window
	图13 X轴翻转工作平台支撑杆应力分析Fig.13 Working platform support rods stress analysis of X-axis rotation

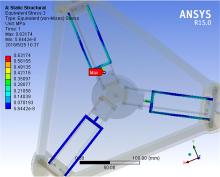
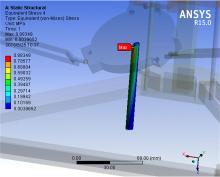
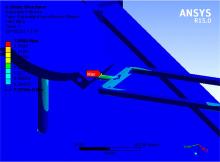
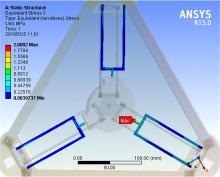
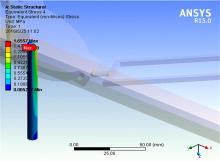
从图10中机构整体应力图中可以清楚地看到, 打印机整体在打印过程中工作平台沿X轴翻转到最大角度静止时, 大部分应力在0.1 MPa左右, 只有在工作平台与工作平台连杆连接处和工作平台支撑杆与底座连接处的应力突然变大。如图12所示, 在工作平台连杆与工作平台连接处应力最大, 最大值为0.51 MPa。从图13中可知, 工作平台支撑杆不均匀受力, 应力最大一侧在0.7 MPa左右, 最小一侧在0.1 MPa。在此工况下, 工作平台连杆与工作平台支撑杆强度均满足要求。

3.2 工作平台沿Y轴翻转时结构应力分析

当工作平台沿X轴翻转时, C₁滑块向上运动, C₂、C₃滑块通过步进电机和同步带在光杠上向下运动。工作平台受力如图14所示。并联机构滑块受到同步带垂直向上的力F₁、F₂、F₃, 工作平台上受到已完成的打印件的重力, 工作平台支撑杆对工作平台有垂直向上的支撑力F₄。

	Figure Option View Download New Window
	图14 工作平台沿Y轴翻转受力图Fig.14 Force diagram of working platform along Y-axis rotation

将结构进行有限元仿真, 得出工作平台Y轴翻转30° 位置打印最大高度时X、Y、Z三个方向的位移, 如图15、图16、图17所示。

	Figure Option View Download New Window
	图15 X方向位移Fig.15 Displacement in X direction

	Figure Option View Download New Window
	图16 Y方向位移Fig.16 Displacement in Y direction

	Figure Option View Download New Window
	图17 结构Z方向位移Fig.17 Displacement in Z direction

从图15中可以清楚地看到, 满载静止时X方向上位移分为上、下两部分:结构上部分X方向位移较大(0.08 mm左右), 且有最大位移点在上三角框上为0.1 mm; 下三角框X方向位移较小可忽略, 立柱上X方向位移是从下到上逐渐变大的。从图16中可以清楚看到, 满载静止时Y方向上位移分为上、下两部分:结构下部分Y方向位移较大(0.04 mm左右), 且有最大位移点在上三角框上为0.045 mm; 上三角框Y方向位移较小可忽略, 立柱上Y方向位移是从下到上逐渐变小的。从图17中可以清楚地看到, 满载静止时Z方向上位移分为两部分:下降滑块立柱一侧Z方向的位移较大且较为平均, 位移都在0.06 mm左右, 而上升和固定滑块两侧的Z方向位移较小, 可以忽略不计。整体在Z方向的位移是从滑块下降一端逐渐向上升滑块两端下降。因此, 整体3个方向的位移较为稳定。

当工作平台X轴翻转时打印最大高度为178.2 mm, 打印材料PLA密度为1.05 g/cm³, 则打印件最大重力为G=π × 40²× 178.2÷ 1000÷ 1000× 9.8=8.77 N。当前市面上喷头结构质量多为350 g, 即3.43 N。在ANSYS中工作平台上加载8.77 N垂直向下的力, 在喷头结构上加载3.43 N垂直向下的力, 得到应力分析图, 如图18~图21所示。

	Figure Option View Download New Window
	图18 Y轴翻转整体应力图Fig.18 Overall stress diagram in Y-axis rotation

	Figure Option View Download New Window
	图19 Y轴翻转并联杆工作平台应力图Fig.19 Parallel working platform stress diagram of Y-axis rotation

	Figure Option View Download New Window
	图20 Y轴翻转工作平台连杆应力分析Fig.20 Working platform links stress analysis of Y-axis rotation

	Figure Option View Download New Window
	图21 Y轴翻转工作平台支撑杆应力分析Fig.21 Working platform support rods stress analysis of Y-axis rotation

从图18中可以清楚地看出, 打印机整体在打印过程中工作平台沿X轴翻转到最大角度静止时大部分应力在0.3 MPa左右, 只有在工作平台与工作平台连杆连接处和工作平台支撑杆与底座连接处的应力突然变大。如图19所示, 在工作平台连杆与工作平台连接处应力最大, 应力最大为2 MPa。由图21可知, 工作平台支撑杆不均匀受力, 应力最大一侧在1.4 MPa左右, 最小一侧在0.1 MPa。在此工况下, 工作平台连杆与工作平台支撑杆强度均满足要求。

4 结束语

为了解决当前3D打印制造过程中一些有悬臂或者空腔结构又不允许添加内部支撑结构的打印件无法制造的问题, 设计了一种工作平台可翻转的3D打印机。分析了其结构组成、运动机理和并联方式。通过对工作平台并联机构空间运动正解与逆解确定其运动实现的可行性。最后, 在CATIA中建立模型, 在ANSYS中完成结构的应力分析, 本文研究为工作平台可翻转的3D打印机的动力学参数优化设计、动态特性等后续研究提供了理论基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	刘伟军. 快速成型技术及应用[M]. 北京: 机械工业出版社, 2005. [本文引用:1]
[2]	钟敏霖, 宁国庆, 刘文今. 激光熔覆快速制造金属零件研究与发展[J]. 激光技术, 2002, 26(5): 388-391. Zhong Min-lin, Ning Guo-qing, Liu Wen-jin. Research and development on laser direct manufacturing metallic components[J]. Laser Technology, 2002, 26(5): 388-391. [本文引用:1]
[3]	柴枫, 赵铱民, 李涤尘. 快速成型技术在医学中的应用[J]. 口腔颌面修复学杂志, 2004, 5(1): 63-65. Chai Feng, Zhao Yi-min, Li Di-chen. Applications of rapid prototyping techniques for medicine[J]. Chinese Journal of Prosthodontics, 2004, 5(1): 63-65. [本文引用:1]
[4]	Stava O, Vanek J, Benes B, et al. Stress relief: improving structural strength of 3D printable object[J]. ACM Transactions on Graphics, 2012, 31(4): article No. 48. [本文引用:1]
[5]	Umetani N, Schmidt R. Cross-sectional structural analysis for 3D printing optimization[C]∥Proceedings of SIGGRAPH Asia 2013 Technical Briefs. New York: ACM Press, 2013: article No. 5. [本文引用:1]
[6]	Chen Y. 3D texture mapping for rapid manufacturing[J]. Computer-Aided Design&Application, 2007, 4(6): 761-771. [本文引用:1]
[7]	Christiansen A N, Schmidt R, Bxrentzen J A. Automatic balancing of 3D models[J]. Computer-Aided Design, 2015, 58: 236-241. [本文引用:1]
[8]	Zhao Jun-wei, Fang Xun, Huang Jun-jie. The forward solution of 3-PRS serial parallel mechanism based on Matlab&Database[J]. Manufacturing Technology & Machine Tool, 2008(6): 233-238. [本文引用:1]
[9]	吴海岭. 3SPS+SP型并联机构的关键理论研究[D]. 秦皇岛: 燕山大学机械学院, 2010. Wu Hai-ling. The critical theory study of 3SPS+SP parallel mechanism[D]. Qinghuangdao: School of Mechanical Engineering, Yanshan University, 2010. [本文引用:1]
[10]	李瑞清. 新型混联式叶片磨抛机床研究[D]长春: 吉林大学机械科学与工程学院, 2011. Li Rui-qing. Study on novel hybrid grinding and polishing machine tool for blade finishing[D]. Changchun: College of Mechanical Science and Engineering, Jilin University, 2011. [本文引用:1]
[11]	康件丽, 陈国强, 赵俊伟. 3-PRS并联机构正解的数值方法[J]. 现代制造工程, 2015(2): 36-42. Kang Jian-li, Chen Guo-qiang, Zhao Jun-wei. Forward kinematics of 3-PRS mechanism based on numerical method[J]. Modern Manufacturing Engineering, 2015(2): 36-42. [本文引用:1]
[12]	王庚祥, 刘宏昭, 原大宁. 空间4-SPS/CU并联机构的受力分析[J]. 农业工程学报, 2012, 28(22): 30-38. Wang Geng-xiang, Liu Hong-zhao, Yuan Da-ning. Force analysis of spatial 4-SPS/CU parallel mechanism[J]. Transactions of the CSAE, 2012, 28(22): 30-38. [本文引用:1]

2005

0.0

... 目前,这一直接制造技术在国内外已经成功应用于航空航天、医疗等领域,推动了先进制造技术的进步,提升了先进制造技术的水平^[1,2,3] ...

2002

0.0

. 2002, 26(5):388-391 DOI:doi:10.3969/j.issn.1001-3806.2002.05.003

Research and development on laser direct manufacturing metallic components

激光熔覆快速制造金属零件研究与发展

Zhong Min-lin , Ning Guo-qing , Liu Wen-jin.

钟敏霖, 宁国庆, 刘文今

This paper summarized the research and development on laser direct manufacturing (LDM) metallic components based on laser cladding technology. The various direct manufacturing methods were introduced with the main emphasis on laser clad based manufacturing technology and its important technological constitutes: high quality coaxial nozzle,optimization of the laser cladding technique and the closed loop control of the process. The typical metallic components produced and the main application fields of LDM were demonstrated. The further research interests on LDM were proposed.

论述了激光快速直接制造的国内外研究和发展现状,介绍了激光快速制造金属零件的方法,重点说明了基于激光熔覆的快速制造技术和激光制造技术涉及的关键问题:精密高质量同轴送粉熔覆系统、激光熔覆的工艺优化与稳定性和激光熔覆过程的检测与闭环控制。展示了激光熔覆快速制造的典型金属零件和应用领域。提出了激光熔覆制造进一步研究的方向。

... 目前,这一直接制造技术在国内外已经成功应用于航空航天、医疗等领域,推动了先进制造技术的进步,提升了先进制造技术的水平^[1,2,3] ...

2004

0.0

... 目前,这一直接制造技术在国内外已经成功应用于航空航天、医疗等领域,推动了先进制造技术的进步,提升了先进制造技术的水平^[1,2,3] ...

2012

0.0

... 由于当前3D打印机对不同结构填充支撑材料方式与填充材料相同,从而存在强度问题^[4,5]、耗材问题^[6]、稳定性问题等^[7],并且一些不允许添加支撑材料的结构就无法进行3D打印 ...

0.0

2007

0.0

2015

0.0

... 1 系统的结构组成和工作原理少自由度并联机构由于具有高刚度、高精度、构造简单、制造和控制相对容易,且便于连接其他机构的优越性,因而广泛应用于独立机构、关节机构、机床工作台、工件定位、微动机构等领域^[8] ...

2010

0.0

. 2010, :-

The critical theory study of 3SPS+SP parallel mechanism[D]. Qinghuangdao: School of Mechanical Engineering,

3SPS+SP型并联机构的关键理论研究[D]

Wu Hai-ling.

吴海岭

随着并联机构技术的发展,少自由度并联机构由于具有结构相对简单,控制容易,造价低等优点,逐步成为机构学领域新的研究热点,在工业生产领域有着广阔的应用前景。本文在分析国内外少自由度并联机构研究与应用的基础上,提出了一种三转一移带有复合球铰的新型4-DOF 3SPS+SP并联机构,并系统地进行了关键理论的研究和数值验证。根据机构的几何约束关系,利用矢量法推导出位置反解表达式,分别得到不含偏导数的Jacobian矩阵和Hessian矩阵。借助CAD变量几何法构建线框式模拟机构,对运动学反解进行了数值验证。基于MATLAB编程,数值算法,快速有效地计算出每组杆长所对应的8组位置正解及其对应的误差。利用双极值法、包络法分别确定了3SPS+SP并联机构可达工作空间和次级工作空间。基于位置反解方程的MATLAB独立变量法,分析了独立参数、杆长限制、球铰范围对工作空间截面的影响。根据虚功原理对机构进行了静力学分析,利用拉格朗日法建立了动力学模型,并推导出系统状态空间方程,为控制系统的设计奠定了基础。利用MATLAB图形用户界面功能(GUI)开发出操作简单适用性较强的四自由度并联机构分析平台,实现了对并联机构的参数化分析。在Proe中建立三维实体,基于ADAMS对机构进行了动态仿真和曲面模拟加工,为实际样机的设计提供了参考依据。

... 并联机构是由两个或两个以上的运动链将固定平台和运动平台连接在一起,驱动装置至少分布在两个或两个以上的分支运动链上,而且一般具有两个或两个以上的自由度^[9] ...

2011

0.0

. 2011, :-

Study on novel hybrid grinding and polishing machine tool for blade finishing[D].

新型混联式叶片磨抛机床研究

Li Rui-qing.

李瑞清

随着汽轮机、涡轮机和航空发动机等轴流叶轮机械的广泛应用,叶片作为重要部件之一,叶片质量直接影响到汽轮机、涡轮机和航空发动机等性能。叶片具有设计过程复杂、由空间复杂曲面组成、工作环境恶劣、精度要求高的特点。因此对叶片的设计、材料、机械加工工艺、热处理及表面喷涂等过程要求很高,设计及制造中任何微小缺陷都会影响工作效率,甚至使整个机组损坏。随着商业CAD软件成熟及广泛应用,叶片设计能力得到了极大提升。但在制造过程中,磨抛精加工工序自动化程度很低,需要大量人工来达到叶片型面精度和表面质量要求,不仅占用大量工时,而且质量往往由加工者经验来保证。为提高叶片表面磨抛精加工自动化程度,提高叶片开发效率,缩短叶片设计生产周期,减少人为因素对叶片精度和表面质量的影响,课题组开发了一种新型混联式磨抛机床,并应用到叶片磨抛工作中,充分结合了并联机构和传统串联机床的优点,不仅可以充分利用并联机构高刚度,高精度,高灵活性和柔性的特点,而且通过串联横梁和床身两个移动自由度,有效地解决了并联机构运动空间小的问题,并能够合理分配运动行程,适应叶片工件特点。通过磨抛工具沿X轴的直线运动和3-RPS运动平台的Z轴移动、绕X轴转动和绕Y轴转动三个自由度运动,带动叶片运动形成复合运动,包勒出叶片四自由度截面型线,再通过串联的床身沿Y轴的进给运动,可以能够加工到叶片整个表面。新型混联式叶片磨抛机床为课题组首次提出,并申请了两项专利,其中一项为发明专利CN101148021,另一项为实用新型专利CN201109062。本文在吉林省科技发展计划重点项目资助下,进行了对新型混联式叶片磨抛机床研究,包括机床所需自由度、自由度分配、传动链配置、核心部件及机床整体结构设计等,现已完成了机床设计开发工作和机床加工装配,进入到机床调试阶段。确立了3-RPS并联机构的独立自由度,并对3-RPS并联机构进行了运动学和动力学分析,建立了并联机构独立自由度与驱动副之间位置、速度、加速度等正反解模型,并利用拉格朗日法建立了并联机构的动力学模型；结合3-RPS并联机构的结构设计和运动学分析,求解了不同位置和姿态角的工作空间。根据叶片结构特点,对机床进行整机运动规划和轨迹规划,将运动分配到机床各主动自由度,进行了混联叶片磨抛机床仿真分析。仿真过程中,由于叶片边缘处曲率变化较大,磨抛加工时会对机床产生冲击。为降低冲击,对叶片边缘处加工点进行插值处理,增加叶片边缘处的数据点,减小运动步距。插值处理后,整个叶片螺旋线磨抛仿真过程平顺,没有明显冲击产生。同时,仿真分析也表明,伺服电机完全满足叶片磨抛过程中的动力要求。通过对机床局部细节和结合面处理,建立了3-RPS并联机构和机床整机有限元模型,并利用有限元分析软件ANSYS分析了机床静态和动态性能。机床静态性能较好,3-RPS并联机构和机床整机刚度均较大；利用有限元和实验法完成机床模态分析,两种方法得到的机床固有频率相近。完成了机床X、Y运动轴的精度检测实验和叶片磨抛单因素实验研究。机床精度检测实验,对机床X、Y运动轴定位精度、重复定位精度和直线度进行检测。叶片磨抛分别对砂带粒度、砂带转速和进给速度三方面进行了单因素实验,实验结果显示,砂带粒度对叶片磨抛效果影响最大,砂带粒度越大、砂带转速越高和进给速度越低则磨削效果越好,可以使叶片达到较低的表面粗糙度。

... 求解运动学逆解就是给定动平台在定坐标系下的坐标,求解静坐标系下3个主动副的位移量^[10] ...

0.0

. , 2015(2):36-42

Forward kinematics of 3-PRS mechanism based on numerical method

3-PRS并联机构正解的数值方法

Kang Jian-li , Chen Guo-qiang , Zhao Jun-wei.

康件丽, 陈国强, 赵俊伟

正解计算是3-PRS并联机构设计与评价的重要工作之一,由于求解3-PRS并联机构的解析表达式十分困难,所以通常求其数值解.针对正解迭代求解时可能由于初始值设置不当引起的求解失败或遗漏真实解的问题,提出了运用蒙特卡洛方法设置迭代初始值.通过大量的随机抽样得到所有可能的解,并且归并这些解,然后绘制3-PRS并联机构的位姿简图,以此来直观判断解的合理性,最后应用算例验证了该方法的有效性及可行性.结果表明:充分利用蒙特卡洛方法的随机性,可以找到所有的解;绘制的3-PRS并联机构位姿简图形象直观,方便对真实解进行判别.

... 求解运动学正解就是给定静坐标系下3个主动副的位移量求解动平台在定坐标系下的坐标^[11] ...

2012

0.0

. 2012, 28(22):30-38 DOI:doi:10.3969/j.issn.1002-6819.2012.22.005

Force analysis of spatial 4-SPS/CU parallel mechanism

空间4-SPS/CU并联机构的受力分析

Wang Geng-xiang , Liu Hong-zhao , Yuan Da-ning.

王庚祥, 刘宏昭, 原大宁

The degree of freedom of a 4-SPS/CU parallel mechanism which can perform three-dimensional rotations and translation along Z axis was analyzed based on the screw theory, and concluded that this parallel mechanism was a non-overconstrained mechanism. By the dismantle-bar method, the static equilibrium equations of the mechanism were set up. The equations' number are more than the unknown variables in the static equilibrium equations (belong to overdetermined equation), and the number of redundant equations were equal to the passive degrees of freedom. All of the forces/torques of each component of the mechanism was obtained by solving the static equilibrium equations which got rid of the redundant equilibrium equations corresponding to passive degree of freedom. The simulation curves of the driving force and constraint reactions were given with change of the mechanism's position and posture. It was confirmed that the mechanism had better carrying capacity than other 4-DOF parallel mechanism without the driven chain. The research results could provide the statics analysis method for the application of engineering and structure design.

运用螺旋理论分析了一种具有三维转动和一维移动（沿Z轴）的四自由度（4-SPS/CU）并联机构的自由度，得出该机构为无过约束机构。采用传统的拆杆法对该机构的每个活动构件进行了静力学分析，得出了该机构的静力学平衡方程组，判定该机构的静力学平衡方程组中方程个数大于未知量个数（属超定方程组）。多余的方程个数就是该机构的局部自由度，并采取去掉局部自由度对应的静力学平衡方程来求解该超定方程组。通过求解该方程组，得出了该机构每个构件上的全部约束力/力矩，并分别得出了驱动力与主运动副以及恰约束从动支链的约束反力随该机构位姿变化的仿真曲线。证实了该机构比无恰约束从动支链的四自由度并联机构拥有更好的承载能力。研究结果可为该机构在工程中的应用与结构设计提供静力学理论分析的参考。

... 3 整体结构应力分析对并联机构进行静应力分析来确定驱动力经并联机构关节后并联机构的传递效果,它是运动学分析的延续和动力学分析、刚度分析的基础,为并联机构的结构尺寸参数设计和动力选择提供理论依据^[12] ...