基于碰撞胸压标定试验的仿真假人材料参数优选法

引用本文

麻凯, 高继东, 闫磊, 徐涛. 基于碰撞胸压标定试验的仿真假人材料参数优选法. 吉林大学学报（工学版）, 2017, 47(5): 1498-1503
MA Kai, GAO Ji-dong, YAN Lei, XU Tao. Dummy material parameter optimization based on calibration experiment of chest pressure in collision. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1498-1503 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705022
Permissions

基于碰撞胸压标定试验的仿真假人材料参数优选法

麻凯^1,², 高继东², 闫磊¹, 徐涛¹

1.吉林大学机械科学与工程学院,长春 130022

2.中国汽车技术研究中心汽车工程研究院,天津 300300

作者简介:麻凯(1978-),男,在站博士后.研究方向:汽车被动安全设计,区间优化理论.E-mail:makai@jlu.edu.cn

基金项目:汽车零部件制造技术与装备吉林省高校高端科技创新平台项目

摘要

基于实车碰撞试验建立了新型仿真有限元假人模型,并提出了相应的参数优化方法。为了提高假人仿真效果与实车试验结果的一致性,需要对假人主要结构材料参数进行调整。首先,提出了参数优选方案,选择出可以显著影响仿真结构的重要参数。然后,采用优化方法得到与实车试验结果近似的有限元假人修正模型。最后,本文以新型仿真有限元假人模型正碰胸压试验为例,对假人胸部相关材料参数按照参数优选法进行筛选,并用优化方法修改结构参数,从而保证仿真假人胸压峰值和回弹率等几个关键指标与实车碰撞下的假人实测数据较为一致。本文所提方法可以用于完善新型仿真有限元假人模型,以满足整车碰撞仿真的需要。

关键词: 机械设计; 整车碰撞; 有限元仿真假人; 参数优化; 参数优选

中图分类号:U463 文献标志码:A 文章编号:1671-5497(2017)05-1498-06

Dummy material parameter optimization based on calibration experiment of chest pressure in collision

MA Kai^1,², GAO Ji-dong², YAN Lei¹, XU Tao¹

1.College of Mechanical Science and Engineering, Jilin University,Changchun 130022, China

2.Automotive Engineering Research Institute,China Automotive Technology &Research Center, Tianjin 300300, China

Abstract

Based on full-size vehicle collision test, a new Finite Element Model (FEM) of dummy is built, and the corresponding parameter optimization method is proposed. To improve the consistency between the results of dummy simulation and full-size collision test, it is necessary to scientifically adjust the major structural material parameters of the FEM of dummy. First, the parameter optimization method is proposed and the important parameters, which significantly affect the simulation results, are selected. Then, the optimal method is applied to obtain the modified FEM of dummy that is similar to that of the full-size vehicle. Finally, taking the chest pressures of some FEMs of dummy in positive collision as examples, the main material parameters of the dummy chest are selected and the structural parameters are modified by the optimization method, thus, ensuring that the chest pressure peak and spring rate of the simulation dummy are consistent with the full-size vehicle collision results. The method proposed in this work can be used to improve the FEM of dummy to meet the requirement of full-size vehicle collision simulation.

Key words: mechanical design; vehicle collision; FEM dummy; parameter optimization; parameter optimal selection

Show Figures

0 引言

整车碰撞仿真中有假人仿真是必不可少的。国外对正碰假人有限元模型的研究与开发方面已积累一定的经验。国际上, 已开发的正面碰撞假人的主要类型包括:50百分位男性假人、95百分位男性假人、5百分位女性假人, 一岁以下的婴儿、3岁幼儿、13岁儿童、老人和孕妇等。目前世界各大汽车公司中广泛采用的正碰有限元假人模型主要由美国FTSS(First technology safely systems)公司及德国DYNAmore公司生产和提供。欧美假人公司生产的正面碰撞和侧碰假人产品早已形成这种系列, 进而在国际上形成了商品和标准。国内对于正面碰撞假人的研究方向主要是对正面碰撞假人进行缩放, 满足中国人体尺寸^{[1, 2]}。陈爽等^[3]基于中国人人体生物学特征和形体尺寸, 建立了对应的有限元模型, 研制了中国95百分位碰撞假人。曹立波等^[4]提出了通过部分体段缩放方法, 达到符合中国50百分位人体的碰撞假人的开发方案。

为了使假人的仿真效果与实车试验的结果相一致, 需要对假人主要结构材料参数和参数曲线进行合理调整。本文就此提出了满足这一要求的参数近似优化设计方法。为了说明方法的应用, 本文以新型假人有限元模型正碰胸压试验为例, 优化设计了某些材料参数^{[5, 6, 7, 8, 9, 10, 11, 12]}。结果表明, 该方法可以用于改进新型假人有限元模型以满足整车碰撞仿真计算准确性的需要。本文先使用灵敏度分析方法对参数进行分析, 并以此为基础数据, 应用广义逆理论和矩阵摄动理论, 研究了新型仿真有限元假人模型胸部主要结构参数的优化问题, 即在均方意义下选取合理的优化参数组合, 总结提出了理想修改参数选取法^[13], 再采用多目标优化方法进行优化。算例中, 本文使用这种方法对假人胸压模型进行了优化参数的选取和多目标优化, 结果证明了该方法的有效性。

1 理想修改参数选取法

设Δ $\begin{matrix} \bar{w} \end{matrix}$ =(Δ $\begin{matrix} {\bar{w}}_{1} \end{matrix}$ , Δ $\begin{matrix} {\bar{w}}_{2} \end{matrix}$ , …, Δ $\begin{matrix} {\bar{w}}_{n} \end{matrix}$ )^T为n个初始值相对优化目标值的偏差量所构成的向量, 另有m个优化参数, 可表示为b₁, b₂, …, b_m, 对应上述n个优化目标的灵敏度矩阵记为:

$\begin{matrix} \bar{U} = {[u_{1}, u_{2}, \dots, u_{m}]}_{n \times m} (1) \end{matrix}$

对于偏差向量Δ $\begin{matrix} \bar{w} \end{matrix}$ , 设从m个设计参数中选取k(k≤ m)个参数, 并将其进行修改, 记为b_i₁, b_i₂, …, b_ik, 矩阵表示为b_i=[b_i₁, b_i₂, …, b_ik], 其对应的灵敏度矩阵为:

$\begin{matrix} U = {[b_{i 1}, b_{i 2}, \dots, b_{ik}]}_{n \times k} (2) \end{matrix}$

由矩阵摄动理论, 当参数b_i₁, b_i₂, …, b_ik的修改量为Δ b_i= $\begin{matrix} {[Δ b_{i 1}, Δ b_{i 2}, \dots, Δ b_{ik}]}^{T} \end{matrix}$ 时, 优化目标的修改量即可记为:

$\begin{matrix} Δw = U \cdot Δb (3) \end{matrix}$

结构经上述修改后, 偏差向量变为:

$\begin{matrix} ψ = Δw + Δ \bar{w} = Δw + U \cdot Δb (4) \end{matrix}$

其均方值即为:

$\begin{matrix} ψ_{rms}^{2} = ψ^{T} ψ = {(Δ w + U \cdot Δb)}^{T} (Δ w + U \cdot Δb) (5) \end{matrix}$

为使 $\begin{matrix} ψ_{rms}^{2} \end{matrix}$ 取最小值, 式(5)对Δ b求导再令其为零, 得到:

$\begin{matrix} U \cdot Δb = - Δ \bar{w} (6) \end{matrix}$

从而得到Δ b对应的最优修改量为:

$\begin{matrix} Δb = U^{+} Δ \bar{w} (7) \end{matrix}$

式中:U⁺为U的Moore-penrose型广义逆。

$\begin{matrix} U^{+} = {U^{T}}_{2} (U_{2} {U^{T}}_{2}) {({U^{T}}_{1} U_{1})}^{- 1} {U^{T}}_{1} (8) \end{matrix}$

这里, U₁、U₂为矩阵的最大值分解项, 其满足

$\begin{matrix} U = U_{1} \cdot U_{2} (9) \end{matrix}$

式中:U₁为n× r列满秩矩阵; U₂为r× k行满秩矩阵; r=rank(U)为灵敏度矩阵U的秩。

将式(7)代入式(5), 再利用广义逆的性质(即式(8)), 解得修改后偏差ψ 的均方值为:

$\begin{matrix} ψ_{rms}^{2} \end{matrix}$ =Δ $\begin{matrix} {\bar{w}}_{rms}^{2} \end{matrix}$ -Δ $\begin{matrix} {\bar{w}}^{T} \end{matrix}$ U₁ $\begin{matrix} {({U^{T}}_{1} U_{1})}^{- 1} \end{matrix} \begin{matrix} {U^{T}}_{1} \end{matrix}$ Δ $\begin{matrix} \bar{w} \end{matrix}$ (10)

偏差向量是一个随机变化的向量, 其协方差阵为 $\begin{matrix} C_{Δ \bar{w} Δ \bar{w}} \end{matrix}$ , 则

$\begin{matrix} E (Δ {\bar{w}}_{rms}^{2}) = E (Δ {\bar{w}}^{T} \cdot Δ \bar{w}) = \overset{n}{\sum_{i = 1}} {(C_{Δ \bar{w} Δ \bar{w}})}_{ii} (11) \end{matrix}$

式中:E为数学期望; $\begin{matrix} {(C_{Δ \bar{w} Δ \bar{w}})}_{ii} \end{matrix}$ 为 $\begin{matrix} C_{Δ \bar{w} Δ \bar{w}} \end{matrix}$ 第i个对角线元素, 即Δ $\begin{matrix} {\bar{w}}_{i} \end{matrix}$ 对应的方差。

引入随机向量:

$\begin{matrix} φ = {L^{T}}_{r \times r} {U^{T}}_{1} Δ \bar{w} (12) \end{matrix}$

式中: $\begin{matrix} {L^{T}}_{r \times r} \end{matrix}$ 为矩阵( $\begin{matrix} {U^{T}}_{1} \end{matrix}$ U₁)^-¹的Cholesky因子, 其满足

$\begin{matrix} {({U^{T}}_{1} U_{1})}^{- 1} = L \cdot L^{T} (13) \end{matrix}$

φ 的协方差矩阵如下:

$\begin{matrix} C_{φφ} = E (φ φ^{T}) = L^{T} {U^{T}}_{1} C_{Δ \bar{w} Δ \bar{w}} U_{1} L (14) \end{matrix}$

由式(10)得到偏差向量ψ 的均方值数学期望为:

$\begin{matrix} E (ψ_{rms}^{2}) = \overset{n}{\sum_{i = 1}} {(C_{Δ \bar{w} Δ \bar{w}})}_{ii} - \overset{n}{\sum_{i = 1}} {(C_{φφ})}_{ii} \end{matrix}$ (15)

从式(15)可以看出, 若从m个设计变量中选取k个变量(b_i₁, b_i₂, …, b_ik)进行修改, 可使修改后的数学期望E( $\begin{matrix} ψ_{rms}^{2} \end{matrix}$ )值最小, 使C_{φ φ}的迹 $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ (C_{φ φ})_ii取最大。记

$\begin{matrix} \tilde{U} = U_{1} L (16) \end{matrix}$

这里, $\begin{matrix} \tilde{U} \end{matrix}$ 中的各个列向量是正交归一化的。式(14)可转化为:

$\begin{matrix} C_{φφ} = {\tilde{U}}^{T} C_{Δ \bar{w} Δ \bar{w}} \tilde{U} (17) \end{matrix}$

再将矩阵 $\begin{matrix} C_{Δ \bar{w} Δ \bar{w}} \end{matrix}$ 的n个特征值和它们对应的特征向量分别表示为:

$\begin{matrix} 0 < λ_{1} \leq λ_{2} \leq \dots \leq λ_{n} 和 a_{1}, a_{2}, \dots, a_{n} (18) \end{matrix}$

r个最大特征值对应的特征向量构成一个n× r的矩阵:

$\begin{matrix} A_{n \times r} = [a_{n - r + 1}, \dots, a_{n}] (19) \end{matrix}$

设 $\begin{matrix} \tilde{U} \end{matrix}$ 使矩阵方程

$\begin{matrix} AX = \tilde{U} (20) \end{matrix}$

有解, 此时X是一个n× r的正交阵, 可得:

$\begin{matrix} \overset{n}{\sum_{i = 1}} {(C_{φφ})}_{ii} = \overset{n}{\sum_{j = n - r + 1}} λ_{j} (21) \end{matrix}$

式(20)和式(21)可证明, 选取适当参数b_i₁, b_i₂, …, b_ik, 可使它对应的灵敏度矩阵U的秩r等于min $\begin{matrix} (k, rank (\bar{U})) \end{matrix}$ , 由于U的列向量可表示为:a_n-r+₁, …, a_n的线性组合, 则有 $\begin{matrix} \overset{r}{\sum_{i = 1}} {(C_{φφ})}_{ii} \end{matrix}$ 取其最大值 $\begin{matrix} \overset{r}{\sum_{j = n - r + 1}} \end{matrix}$ λ _j, 偏差向量ψ 的均方值期望得到最小值, 即 $\begin{matrix} \overset{n - r}{\sum_{j = 1}} \end{matrix}$ λ _j, 所以, 这里可以把b_i₁, b_i₂, …, b_ik看作理想修改参数。

2 多目标优化

本文使用的多目标优化方法是一种线性多目标迭代近似优化方法, 该方法在工程中已被广泛的应用。主要步骤如下:

步骤1 设一个极小值Δ x, 差分计算函数的灵敏度。

$\begin{matrix} d f_{k} / d x_{i} = \frac{f_{k} (x_{1}, x_{2}, \dots, x_{i} + Δx, \dots, x_{n}) - f_{k} (X)}{Δx} \end{matrix}$ （22）

步骤2 计算

$\begin{matrix} \begin{matrix} f = \frac{d f_{j} / d x_{i}}{d f_{k} / d x_{i}} \\ k, j = 1, 2, \dots m i = 1, 2, \dots, n \end{matrix} \end{matrix}$ （23）

步骤3 用如下方程组求λ ₁, λ ₂, …, λ _m。

$[\begin{matrix} \overset{n}{\sum_{i = 1}} \frac{d f_{1} / d x_{i}}{d f_{1} / d x_{i}} & \overset{n}{\sum_{i = 1}} \frac{d f_{1} / d x_{i}}{d f_{2} / d x_{i}} & \dots & \overset{n}{\sum_{i = 1}} \frac{d f_{1} / d x_{i}}{d f_{m} / d x_{i}} \\ \overset{n}{\sum_{i = 1}} \frac{d f_{2} / d x_{i}}{d f_{1} / d x_{i}} & \overset{n}{\sum_{i = 1}} \frac{d f_{2} / d x_{i}}{d f_{2} / d x_{i}} & \dots & \overset{n}{\sum_{i = 1}} \frac{d f_{2} / d x_{i}}{d f_{m} / d x_{i}} \\ ⋮ & ⋮ & ⋮ \\ \overset{n}{\sum_{i = 1}} \frac{d f_{m} / d x_{i}}{d f_{1} / d x_{i}} & \overset{n}{\sum_{i = 1}} \frac{d f_{m} / d x_{i}}{d f_{2} / d x_{i}} & \dots & \overset{n}{\sum_{i = 1}} \frac{d f_{m} / d x_{i}}{d f_{m} / d x_{i}} \end{matrix}] {∙ [\begin{matrix} λ_{1} \\ λ_{2} \\ ⋮ \\ λ_{m} \end{matrix}]}^{T} = [\begin{matrix} Δ f_{1} (X) \\ Δ f_{2} (X) \\ ⋮ \\ Δ f_{m} (X) \end{matrix}]$ （24）

步骤4 计算

$\begin{matrix} Δ x_{i} = λ_{1} \frac{d f_{1}}{d x_{i}} + λ_{2} \frac{d f_{2}}{d x_{i}} + λ_{3} \frac{d f_{3}}{d x_{i}} \end{matrix}$ （25）

步骤5 计算

$\begin{matrix} Δ f_{k} (X) = f_{k} (X + ΔX) - f_{k} (X) (26) \end{matrix}$

如果 $\begin{matrix} ‖Δ f_{k} (X) - Δ f_{kmax} (X) ‖_{f} \end{matrix}$ ≤ ε , 停止计算; 否则令

$\begin{matrix} d f_{k} / d x_{i} = \frac{f_{k} (x_{1}, x_{2}, \dots, x_{i} + Δ x_{i} + Δx, \dots, x_{n}) - f_{k} (X)}{Δx} \end{matrix}$ (27)

回到步骤2。这里, ε 为一个给定的阈值。

3 材料参数筛选和优化方法

本文对某型有限元假人进行胸部刚性摆锤撞击试验, 对优化后的主要影响参数参照真实假人模型试验结果进行改进, 合理调整胸部压缩变形量和回弹率。

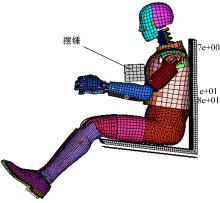
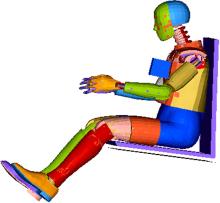
正碰假人模型是参数化的有限元模型, 如图1和图2所示, 其初始模型和实际碰撞假人在胸压曲线等方面还有一定的偏差, 所以调整假人模型的参数是一个十分重要的工作。由于可修改参数多, 标定目标值多, 需要制定一个合理的标定方法, 即筛选出对目标结果影响显著的参数, 并确定这些参数的修改量已达到标定要求。根据上述提到的方法, 总结主要步骤如下:

(1)使用参数优选法从已有的可修改参数中选取对目标结果影响显著的参数, 即理想参数, 如式(1)~(21)所示。

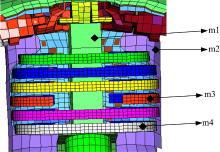
(2)使用多目标优化方法优化目标曲线, 如图3和式(22)~(27)所示。

	Figure Option View Download New Window
	图1 正碰胸压试验Fig.1 Positive chest pressure test

	Figure Option View Download New Window
	图2 正碰胸压试验结果Fig.2 Test results of positive chest pressure

4 算例

试验将某新型有限元仿真假人安置在简易靠背和座椅上, 采用某材料为刚性材料、质量为10 kg、体积为70 mm× 100 mm× 111 mm的摆锤, 摆锤的中心与假人第一个肋骨水平, 处于假人垂直中心位置。正碰胸压试验模型如图1所示。假人胸部主要结构如图3所示。对摆锤设置8.041 m/s的速度撞击新型有限元假人, 使假人的胸压变形量峰值D达到50 mm, 在正碰胸压曲线上分别取下降和上升最为明显的一段曲线的斜率作为曲线的下降斜率K₁和上升斜率K₂。正碰胸压曲线如图4所示。

	Figure Option View Download New Window
	图3 假人胸部结构Fig.3 Dummy chest structure

	Figure Option View Download New Window
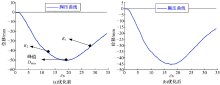	图4 优化前、后的正碰胸位移压随时间的变化曲线Fig.4 Curves of positive chest pressure with time before and after optimization

胸部曲线评价指标值如下:假人胸压峰值D_max=50 mm, 假人胸压曲线下降斜率K₁=3.83359, 假人胸压曲线上升斜率K₂=2.10462。

胸部主要部件材料的初始可修改参数如表1所示, 用“ 部件_编号” 来区分不同部件材料和同种材料不同的可修改参数, 共计可修改参数8个。

表1 初始参数值 Table 1 Initial parameter value

设计目标如下:选取理想参数, 假人胸压峰值D_max=40 mm, 假人胸压曲线下降斜率绝对值 $\begin{matrix} |K_{1}| \end{matrix}$ =3, 假人胸压曲线上升斜率绝对值 $\begin{matrix} |K_{2}| \end{matrix}$ =3。其中, K₁为下降段曲线的近似取值, K₂同理。

采用本文方法对该假人进行了优化。通过参数优选法从8个已知可修改参数中选定了5个理想参数, 见表2。然后, 使用多目标优化方法得到优化解, 见表3。从优化结果上看, 优化目标和实体碰撞假人胸压指标基本一致, 说明仿真假人仿真效果能够满足碰撞试验要求, 即将来的碰撞试验的假人伤害仿真效果可信。优化解相对设计优化目标偏差量较小, 满足工程设计要求。

表2 优选法选取的参数及优化后的参数值 Table 2 Selection of parameters based on optimization method and optimized parameter values

表3 胸部曲线的评价指标值 Table 3 Chest pressure curve evaluation

5 结束语

将参数优选法和多目标优化方法相结合形成了一种高效的优化计算方法。同时本文将工程中经常遇到的曲线优化问题转变对曲线目标点的优化, 即多目标优化问题, 使其优化目标更加直观。这样, 曲线优化问题可以简化、优化参数可以筛选、优化精度得到保证, 从而提高了工程优化问题计算的效率。最后, 本文在算例中的正碰假人胸压曲线标定中使用了该方法, 进一步证明了该方法的可行性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	中国汽车技术研究中心. C-NCAP中国新车评价规程[Z]. [本文引用:1]
[2]	郝霆, 王雍. 汽车碰撞试验及hybrid Ⅲ (假人)应用分析[J]. 城市车辆, 2003(1): 21-23. Hao Ting, Wang Yong. Application analysis of vehicle crash test and hybrid Ⅲ dummy[J]. Urban Vehicles, 2003(1): 21-23. [本文引用:1]
[3]	陈爽, 袁中凡, 林大全, 等. 国产碰撞假人的设计与分析[J]. 四川大学学报, 2008, 40(3): 178-182. Chen Shuang, Yuan Zhong-fan, Lin Da-quan, et al. Design and analysis of Chinese crash dummy[J]. Journal of Sichuan University, 2008, 40(3): 178-182. [本文引用:1]
[4]	曹立波, 黄新刚, 戴黄伟, 等. 基于中国人体特征的正面碰撞假人的开发策略探讨[J]. 中国机械工程, 2014, 25(10): 1410-1414. Cao Li-bo, Huang Xin-gang, Dai Huang-wei, et al. Development strategy of frontal crash dummy based on Chinese human body[J]. China Mechanical Engineering, 2014, 25(10): 1410-1414. [本文引用:1]
[5]	王涛, 陶薇. 重型载货汽车悬架参数的多目标优化设计[J]. 组合机床与自动化加工技术, 2008(11): 29-31. Wang Tao, Tao Wei. Multi-objective optimization of heavy truck suspension parameters[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2008(11): 29-31. [本文引用:1]
[6]	管欣, 逢淑一, 詹军. 汽车悬架运动学特性参数优化方法[J]. 哈尔滨工业大学学报, 2011, 43(1): 145-148. Guan Xin, Feng Shu-Yi, Zhan Jun. Optimization of suspension kinematics characteristic parameters[J]. Journal of Harbin Institute of Technology, 2011, 43(1): 145-148. [本文引用:1]
[7]	麻凯, 陈塑寰. 结构优化中的海森矩阵的近似迭代方法[J]. 吉林大学学报: 工学版, 2006, 36(1): 30-33. Ma Kai, Chen Su-huan. Iterative approximation algorithm of Hessian matrix in structural optimization[J]. Journal of Jilin University (Engineering and Technology Edition), 2006, 36(1): 30-33. [本文引用:1]
[8]	陈塑寰, 麻凯. 板壳加筋结构的组合优化[J]. 吉林大学学报: 工学版, 2008, 38(2): 388-392. Chen Su-huan, Ma Kai. Combined optimization method of plate-shell structures with stiffeners[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(2): 388-392. [本文引用:1]
[9]	麻凯, 陈塑寰. 结构区间参数的二阶近似动态优化方法[J]. 东北大学学报, 2008(增刊2): 221-224. Ma Kai, Chen Su-huan. Approximation algorithm of Hessian matrix in interval optimization of dynamic analysis for structures with interval parameters[J]. Journal of Northeastern University, 2008, 38(Sup. 2): 221-224. [本文引用:1]
[10]	Wu Jie, Shangguan Wen-bin, Chen Su-huan, et al. Improved dynamic optimization method for uncertain structures with interval parameters[J]. Noise and Vibration Control, 2008, 28(1): 27-32. [本文引用:1]
[11]	Chen Su-huan, Wu Jie, Chen Yu-dong. Interval optimization for uncertain structures[J]. Finite Elements in Analysis and Design, 2004, 40: 1379-1398. [本文引用:1]
[12]	Chen Su-huan, Wu Jie. Interval optimization of dynamic response for uncertain structures with natural frequency constraints[J]. Engineering Structures, 2004, 26: 221-232. [本文引用:1]
[13]	麻凯, 管欣, 李鹏. 悬架运动学特性优化中的参数选取方法[J]. 汽车工程, 2013, 35(6): 517-520. Ma Kai, Guan Xin, Li Peng. Parameter selection method in optimization of suspension kinematics characteristics[J]. Automotive Engineering, 2013, 35(6): 517-520. [本文引用:1]

0.0

. , :-

中国汽车技术研究中心

... 国内对于正面碰撞假人的研究方向主要是对正面碰撞假人进行缩放,满足中国人体尺寸^[1,2] ...

0.0

... 国内对于正面碰撞假人的研究方向主要是对正面碰撞假人进行缩放,满足中国人体尺寸^[1,2] ...

2008

0.0

. 2008, 40(3):178-182

Design and analysis of Chinese crash dummy

国产碰撞假人的设计与分析

Chen Shuang , Yuan Zhong-fan , Lin Da-quan

陈爽, 袁中凡, 林大全

... 陈爽等^[3]基于中国人人体生物学特征和形体尺寸,建立了对应的有限元模型,研制了中国95百分位碰撞假人 ...

2014

0.0

. 2014, 25(10):1410-1414

Development strategy of frontal crash dummy based on Chinese human body

基于中国人体特征的正面碰撞假人的开发策略探讨

Cao Li-bo , Huang Xin-gang , Dai Huang-wei

曹立波, 黄新刚, 戴黄伟

... 曹立波等^[4]提出了通过部分体段缩放方法,达到符合中国50百分位人体的碰撞假人的开发方案 ...

0.0

. , 2008(11):29-31 DOI:doi:10.3969/j.issn.1001-2265.2008.11.008

Multi-objective optimization of heavy truck suspension parameters

重型载货汽车悬架参数的多目标优化设计

Wang Tao , Tao Wei.

王涛, 陶薇

为了提高汽车平顺性、安全性并减少轮胎对路面的动载.以某1/2载货汽车的弹簧刚度和阻尼系数为设计参数,以最大动挠度为约束条件,以车身垂直加速度、前后轮胎动栽荷的均方根值为目标函数,运用多目标遗传算法求得三目标的帕莱托解集,经过后期决策得到不同要求下的最优解.结果表明:优化后的悬架弹簧刚度减少而阻尼系数增大,前悬比后悬变化小,性能有大幅度改善,而且采用先寻优后决策的求解模式,能有效弱化先验知识不足的影响,避免局部最优问题,较传统多目标优化方法更为实用有效.

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2011

0.0

. 2011, 43(1):145-148

Optimization of suspension kinematics characteristic parameters

汽车悬架运动学特性参数优化方法

Guan Xin , Feng Shu-Yi , Zhan Jun.

管欣, 逢淑一, 詹军

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2006

0.0

. 2006, 36(1):30-33

Iterative approximation algorithm of Hessian matrix in structural optimization

结构优化中的海森矩阵的近似迭代方法

Ma Kai , Chen Su-huan.

麻凯, 陈塑寰

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2008

0.0

. 2008, 38(2):388-392

Combined optimization method of plate-shell structures with stiffeners

板壳加筋结构的组合优化

Chen Su-huan , Ma Kai.

陈塑寰, 麻凯

提出了一种将结构加筋布局优化和结构参数优化相结合的优化方法。该方法先对结构中的加强筋进行布局优化,然后再优化结构参数。在加筋布局优化中,用单元应变能密度灵敏度作为删除单元的准则。在参数优化中,目标函数和约束函数被近似地表示为二阶表达式,并用改进的DFP(Davidon,Fletcher and Powell)方法来求优化解。为了降低计算复杂度,采用组合近似(CA)方法对修改后的结构位移和应力进行重分析,并应用该方法对储水箱结构进行了结构优化设计。数值结果表明,该方法处理板壳加筋结构优化问题十分有效,而且容易在计算机上实现。

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2008

0.0

. 2008, 2008(增刊2):221-224

Approximation algorithm of Hessian matrix in interval optimization of dynamic analysis for structures with interval parameters

结构区间参数的二阶近似动态优化方法

Ma Kai , Chen Su-huan.

麻凯, 陈塑寰

工程结构中的分析和设计方法一般是基于确定性的结构参数和确定性的数学模型。然而,实际上经常存在着与材料性质、几何特性、外力、初始条件、边界条件及与结构部件接头有关的误差或不确定性。尽管概率统计方法在描述结构力学中的不确定现象方面获得了很大成功,但是在没有足够的实验数据证明由联合概率密度(联合概率密度函数)所给出的假设是正确的情况下,这种方法并不能给出满足某种精度的可靠结果。目前,除了概率统计方法外,用于研究不确定性问题的方法还有凸分析法、模糊集合法和区间分析法。凸分析法和模糊集合法则都受到主观信息的限制,而区间方法研究的大都是线性的区间优化方法,非线性的区间优化问题很少有人研究。所以本文主要讨论了非线性的区间参数的动态优化问题。在本论文主要做了下面的一些工作: 1.提出了区间优化模型,其中目标函数和和约束函数都是区间的。由于直接求解区间优化问题非常困难,所以,结合泰勒展开和函数的区间扩张给出了与区间优化问题二阶近似近似优化问题的数学模型。 2.利用朗格朗日乘子法将带约束的区间优化问题转化为非约束的区间参数优化问题,在利用海森矩阵的近似迭代计算二阶近似区间参数动态优化。 3.在I—DEAS软件上开发结构参数参数的二阶近似优化软件。

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2008

0.0

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2004

0.0

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2004

0.0

... 为了说明方法的应用,本文以新型假人有限元模型正碰胸压试验为例,优化设计了某些材料参数^{[5,6,7,8,9,10,11,12]} ...

2013

0.0

. 2013, 35(6):517-520 DOI:doi:10.3969/j.issn.1000-680X.2013.06.008

Parameter selection method in optimization of suspension kinematics characteristics

悬架运动学特性优化中的参数选取方法

Ma Kai , Guan Xin , Li Peng.

麻凯, 管欣, 李鹏

本文中结合摄动理论和广义逆理论,研究了悬架运动学特性优化中的参数选取问题。提出了两种参数选取方法:理想修改参数选取法和最优修改参数选取法。在双横臂独立悬架运动学特性优化实例中,分别采用两种方法进行优化参数的选取。结果表明两种方法均可满足优化的要求。

... 本文先使用灵敏度分析方法对参数进行分析,并以此为基础数据,应用广义逆理论和矩阵摄动理论,研究了新型仿真有限元假人模型胸部主要结构参数的优化问题,即在均方意义下选取合理的优化参数组合,总结提出了理想修改参数选取法^[13],再采用多目标优化方法进行优化 ...