神光-III精密装校平台运动学分析

引用本文

谢志江, 吴小勇, 范乃吉, 郭宗环, 袁岳军, 王康. 神光-III精密装校平台运动学分析. 吉林大学学报（工学版）, 2017, 47(5): 1504-1511
XIE Zhi-jiang, WU Xiao-yong, FAN Nai-ji, GUO Zong-huan, YUAN Yue-jun, WANG Kang. Kinematics analysis of a precision assembly platform of SG-III. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1504-1511 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705023
Permissions

神光-III精密装校平台运动学分析

谢志江¹, 吴小勇¹, 范乃吉², 郭宗环¹, 袁岳军¹, 王康¹

1.重庆大学机械传动国家重点实验室,重庆 400044

2.中国工程物理研究院激光聚变研究中心,四川绵阳 621900

作者简介:谢志江(1962-),男,教授,博士生导师.研究方向:机械创新设计,机电一体化及设备故障诊断.E-mail:xzj99@vip.sina.com

基金项目:国家自然科学基金项目(U1530138)

摘要

针对神光-III激光装置光机模块装校需要,设计了一套具有6自由度精密调整功能的混联装校平台。运用解析法建立了模块位姿与各姿态调整机构位姿的映射关系,进而求得系统运动学逆解。利用运动学逆解结果,采用BP神经网络实现驱动位移到模块位姿的非线性映射,从而获得系统运动学正解。为提高运动学正解精度,提出采用“单一输出”细分子网络,使得正解精度提高了一个数量级。为进一步提高位置精度,提出了一种对神经网络进行改进的位置补偿算法,使得位置精度提高至10^-3 mm级,满足工程应用要求。MATLAB仿真验证了该方法的可靠性,并可有效应用于求解一般混联机构的运动学正、逆解。

关键词: 机械设计; 运动学; 神经网络; 位置补偿; 混联机构

中图分类号:TP242 文献标志码:A 文章编号:1671-5497(2017)05-1504-08

Kinematics analysis of a precision assembly platform of SG-III

XIE Zhi-jiang¹, WU Xiao-yong¹, FAN Nai-ji², GUO Zong-huan¹, YUAN Yue-jun¹, WANG Kang¹

1.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China

2.Research Center of Laser Fusion, China Academy of Engineering Physics, Mianyang 621900, China

Abstract

A 6-DOF hybrid precision assembly platform was designed to assemble the optical and mechanical modules of the huge laser facility SG-III. Based on analytic method, the position and posture mapping relationship between the pose module and pose adjusting mechanism was established, and then the invert kinematics was obtained. By employing BP neural network, the nonlinear mapping model from driving displacements to the pose module positions and postures was built, and the forward kinematics was acquired by training the inverse kinematics samples. In order to improve the accuracy of the forward kinematics, the network was divided into six sub-networks corresponding of each DOF, thus, the accuracy of the solution was increased by one order of magnitude. Finally, position compensation algorithm was proposed to optimize the network. The results demonstrate the displacement accuracy is enhanced to level 10^-3 mm, which meets the requirement of engineering application. The reliability of the proposed methods is validated by simulation in MATLAB software, which can be applied to solve the forward and inverse kinematics of common hybrid robots.

Key words: mechanical design; kinematics; neural network; position compensation; hybrid robot

Show Figures

0 引言

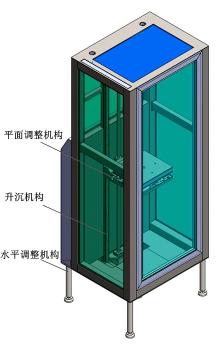
惯性约束聚变(ICF)是产生聚变反应的一种方法, 实现ICF反应必须提供高密度、高能量的激光束。神光-III激光装置是我国目前功率最高、能量最大、最先进的ICF装置^[1], 在其光学回路中安装有一系列不同规则的光机模块, 这类光机模块称为在线可替换单元(LRU)。基于LRU模块制造精密、造价昂贵、洁净度高、质量大等原因, 在装校和拆卸LRU模块时需要一套可实现6自由度精密调整的装校平台^[2], 该装校平台主要由水平调整机构、升沉机构以及平面调整机构混联组成。

混联机构作为串联机构和并联机构的结合体, 既克服了并联机构工作空间小、运动不灵活的缺点, 又解决了串联机构精度、刚度及实时控制方面的不足, 兼具并联机构刚度大和串联机构工作空间大的优点, 是机构学重要的研究方向之一^[3]。混联机构结构形式多种多样, 所涉及的理论研究亦较为广泛。Kanaan等^[4]研制了一台5轴混联机床, 并对其运动学正逆解进行了研究。王瑞等^[5]设计了一种新型混联加工中心, 结合解析法和数值法对其位姿正逆解进行了分析。Tanev^[6]运用封闭解法研究了一种新型混联机构的运动学特性。孙涛等^[7]发明了一种混联可重构机械手, 针对其静刚度进行了全域预估。Gherman等^[8]建立了PARASURG-5M混联医疗机器人动力学逆解模型, 并用于该机构的动力控制。Ibrahim等^[9]采用递归法研究了Logabex LX4混联机器人的动力学特性。Campos等^[10]基于阿苏尔杆组法剖析了混联机构的型综合问题。Zeng等^[11]运用群论对混联机构进行了构型分析。Wang等^[12]对一种移动冗余混联机器人进行了误差补偿。针对EXE-M混联机器人, 潘伯钊等^[13]提出了基于激光跟踪仪的快速零点标定技术。Gallardo-Alvarado^[14]、罗华^[15]等分析了混联机构的灵巧度, 陈小立^[16]、史家顺^[17]等则用不同的算法对相应混联机器人进行了轨迹规划。

本文对所设计混联平台进行了详细的运动学分析, 提出以各姿态调整机构位姿为中间变量构建系统运动学逆解模型, 降低了系统运动学逆解的求解难度, 所得逆解结果为解析值, 无理论误差。利用BP神经网络及其改进算法获得系统运动学正解, 正解精度得到有效提高, 满足工程实际应用。

1 神光-Ⅲ 精密装校平台

神光-III精密装校平台如图1所示, 主要由4-SPU/PS水平调整机构、升沉机构、3-PPR平面调整机构混联组成, 充分结合了并联机构刚度大以及串联机构工作空间大的优点, 满足6自由度精密装校要求。

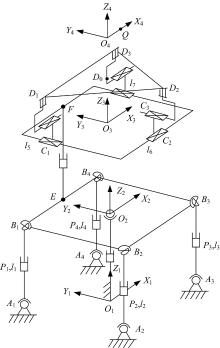
	Figure Option View Download New Window
	图1 神光-III精密装校平台Fig.1 Precision assembly platform of SG-III

装校平台结构简图如图2所示, 其中4-SPU/PS水平调整机构主要由动平台B₁B₂B₃B₄、4条SPU驱动支链及一条PS随动支链组成, 该并联机构具有4个自由度, 分别为绕X、Y、Z轴的旋转以及沿Z轴的平移, 通过驱动移动副P_i便可实现机构的水平调整功能。升沉机构由丝杠导轨组构成, 实现沿Z轴的大行程平移。3-PPR平面调整机构主要由基座C₁C₂C₃、动平台D₁D₂D₃及3条PPR支链组成, 该并联机构具有3个自由度, 分别为沿X、Y向的平移以及绕Z轴的旋转。通过驱动3个移动副C_i便可实现机构的平面调整功能。

	Figure Option View Download New Window
	图2 装校平台结构简图Fig.2 Sketch map of the assembly platform

通过混联后, 该装校平台实质为4-SPU/PS+P+3-PPR混联机构, 并将具有6自由度精密调整功能。

2 运动学逆解

实际装校过程中, 因机构自身结构尺寸限制, 4-SPU/PS水平调整机构绕Z轴旋转角度范围有限, 故在做运动学逆解分析时, Z轴旋转角调整由3-PPR平面调整机构实现。同时升沉机构主要提供沿Z轴的大行程平移, 不适宜用于精密定位, 故在进行姿态精密调整时, 升沉机构保持行程不变, Z轴的精确位移由4-SPU/PS水平调整机构提供, 即系统6自由度姿态精密调整功能主要由4-SPU/PS水平调整机构及3-PPR平面调整机构协调完成。如图2所示, 在4-SPU/PS水平调整机构基座A₁A₂A₃A₄及其动平台B₁B₂B₃B₄中心分别建立全局坐标系O₁和局部坐标系O₂, 同时在3-PPR平面调整机构基座及LRU模块中心分别建立局部坐标系O₃、O₄, 其中LRU模块通过专用工装固定安装于动平台D₁D₂D₃之上。已知LRU模块中心在全局坐标系O₁中的位姿(x, y, z, α , β , γ ), 求解各驱动位移量l_i即为运动学逆解。

对于并联机构而言, 通过坐标变换可以较容易得到其运动学逆解, 而求解混联机构运动学逆解则需建立相对复杂的数学模型, 其计算公式推导及计算过程繁复, 并且因机构差异而不具通用性。针对本文所设计的混联机构, 很难直接构建LRU模块位姿与驱动位移量之间的数学模型, 因此提出以各姿态调整机构的位姿为中间变量, 构建系统运动学逆解模型。

2.1 姿态调整机构位姿

假设局部坐标系O₄相对局部坐标系O₃的位姿(x₁, y₁, d₁, 0, 0, γ ₁), 局部坐标系O₂相对全局坐标系O₁的位姿(0, 0, z₁, α ₁, β ₁, 0), 其中x₁、y₁、z₁为对应的位置参数, α ₁、β ₁、γ ₁为对应的姿态角参数, d₁为D₀到坐标系O₄原点的Z向距离。此时求解各姿态调整机构位姿的关键在于构建(x₁, y₁, z₁, α ₁, β ₁, γ ₁)与(x, y, z, α , β , γ )的函数关系, 以求解局部坐标系O₄坐标原点在全局坐标系O₁中的位置矢量为例介绍两者函数关系的建立。

通过各姿态调整机构的位姿可以求得局部坐标系O₄坐标原点在全局坐标系O₁中的位置矢量:

$O_{4}^{1} =_{2}^{1} R (_{3}^{2} R (_{4}^{3} R O_{4}^{4} + P_{O_{4}}^{3}) + P_{O_{3}}^{2}) + P_{O_{2}}^{1}$ (1)

式中：

$\begin{matrix} \begin{matrix} P_{O_{4}}^{3} = {(\begin{matrix} x_{1} & y_{1} & d_{2} \end{matrix})}^{T} \\ P_{O_{3}}^{2} = {(\begin{matrix} 0 & 0 & d_{3} \end{matrix})}^{T} \\ P_{O_{2}}^{1} = {(\begin{matrix} 0 & 0 & z_{1} \end{matrix})}^{T} \\ _{4}^{3} R = R (z, γ_{1}),_{3}^{2} R = E \\ _{2}^{1} R = R (y, β_{1}) R (x, α_{1}) \end{matrix} \end{matrix}$

$\begin{matrix} P_{O_{i}}^{j} \end{matrix}$ 为坐标系O_i相对O_j位置矢量 $\begin{matrix} ;_{i}^{j} \end{matrix}$ R为坐标系O_i相对O_j方向余弦矩阵; R(x, α ₁)、R(y, β ₁)、R(z, γ ₁)分别为绕x、y、z轴的旋转变换矩阵^[18]; E为三阶单位矩阵; d₂为坐标系O₃到O₄的Z向距离; d₃为坐标系O₂到O₃的Z向距离。

局部坐标系O₄坐标原点在全局坐标系O₁中的位置矢量可以直接通过局部坐标系O₄相对全局坐标系O₁的位姿变换求得:

$O_{4}^{1} =_{4}^{1} R O_{4}^{4} + P_{O_{4}}^{1}$ （2）

式中：

$O_{4}^{4} = {(\begin{matrix} 0 & 0 & 0 \end{matrix})}^{T}$

$P_{O_{4}}^{1} = {(\begin{matrix} x & y & z \end{matrix})}^{T}$

$\begin{matrix} _{4}^{1} R = R (z, γ) R (y, β) R (x, α) \end{matrix}$

联立式(1)(2)可得:

$\begin{matrix} \{\begin{matrix} x_{1} \cos β_{1} + y_{1} \sin β_{1} \sin α_{1} + d_{4} \sin β_{1} \cos α_{1} = x \\ y_{1} \cos α_{1} - d_{4} \sin α_{1} = y \\ - x_{1} \sin β_{1} + y_{1} \cos β_{1} \sin α_{1} + d_{4} \cos β_{1} \cos α_{1} = z \end{matrix} \end{matrix}$ (3)

同理, 在局部坐标系O₄内取两点D₀、Q, 其中D₀为Z₄轴负方向与动平台D₁D₂D₃相交点, Q位于X₄轴正方向, 距坐标原点一个单位长度, 满足:

$D_{0}^{1} =_{2}^{1} R (_{3}^{2} R (_{4}^{3} R D_{0}^{4} + P_{O_{4}}^{3}) + P_{O_{3}}^{2}) + P_{O_{2}}^{1} =_{4}^{1} R D_{0}^{4} + P_{O_{4}}^{1}$ （4）

$\begin{matrix} Q^{1} =_{2}^{1} R (_{3}^{2} R (_{4}^{3} R Q^{4} + P_{O_{4}}^{3}) + {P^{2}}_{O_{3}}) + {P^{1}}_{O_{2}} =_{4}^{1} R Q^{4} + P_{O_{4}}^{1} \end{matrix}$ (5)

由式(4)(5)分别求得:

$\begin{matrix} \{\begin{matrix} x_{1} \cos β_{1} + y_{1} \sin β_{1} \sin α_{1} + d_{5} \sin β_{1} \cos α_{1} = \\ x - d_{1} (cosγsinβcosα + sinγsinα) \\ y_{1} \cos α_{1} - d_{4} \sin α_{1} = y - \\ d_{1} (sinγsinβ cosα - cosγsinα) \\ - x_{1} \sin β_{1} + y_{1} \cos β_{1} \sin α_{1} + \\ d_{4} \cos β_{1} \cos α_{1} = z - d_{1} cosβcosα \end{matrix} \end{matrix}$ (6)

$\begin{matrix} \{\begin{matrix} x_{1} \cos β_{1} + y_{1} \sin β_{1} \sin α_{1} + d_{4} \sin β_{1} \cos α_{1} + \\ \cos γ_{1} \cos β_{1} + \sin γ_{1} \sin β_{1} \sin α_{1} = \\ x + cosγcosβ \\ y_{1} \cos α_{1} - d_{4} \sin α_{1} + \sin γ_{1} \cos α_{1} = \\ y + sinγcosβ \\ - x_{1} \sin β_{1} + y_{1} \cos β_{1} \sin α_{1} + d_{4} \cos β_{1} \\ \cos α_{1} - \cos γ_{1} \sin β_{1} + \sin γ_{1} \cos β_{1} \sin α_{1} + \\ z_{1} = z - sinβ \end{matrix} \end{matrix}$ (7)

式中:d₄=d₂+d₃, d₅=d₄-d₁。

联立方程组(3)(6)(7)解得:

$\begin{matrix} \{\begin{matrix} α_{1} = arcsinB \\ β_{1} = \arcsin \frac{A}{\sqrt[]{A^{2} + C^{2}}} \\ γ_{1} = \arcsin \frac{D}{\sqrt[]{A^{2} + C^{2}}} \\ x_{1} = \frac{1}{C \sqrt[]{A^{2} + C^{2}}} \cdot \\ [(A^{2} + C^{2}) x - ABy - d_{4} A] \\ y_{1} = \frac{y + d_{4} B}{\sqrt[]{A^{2} + C^{2}}} \\ z_{1} = z + \frac{1}{C} (Ax - By - d_{4}) \end{matrix} \end{matrix}$ (8)

式中:A=cosγ sinβ cosα +sinγ sinα

B=cosγ sinα -sinγ sinβ cosα

C=cosβ cosα

D=sinγ cosβ

至此, 已完整求得各姿态调整机构位姿, 不难发现, α ₁、β ₁、γ ₁只与α 、β 、γ 有关, 并且呈现高度的非线性特性, 而位移x₁、y₁、z₁与末端位姿的关系更为复杂、耦合性更强。

2.2 系统逆解

在求得各姿态调整机构位姿后, 求解系统运动学逆解相对比较容易。对于4-SPU/PS水平调整机构, B_i在局部坐标系O₂中位置矢量 $\begin{matrix} B_{i}^{2} \end{matrix}$ 以及A_i在全局坐标系O₁中位置矢量 $\begin{matrix} A_{i}^{1} \end{matrix}$ 均可由机构几何尺寸直接得出, 通过坐标变换可以求得B_i在全局坐标系O₁中位置矢量:

$\begin{matrix} B_{i}^{1} =_{2}^{1} R B_{i}^{2} + P_{O 2}^{1} (9) \end{matrix}$

从而求得水平调整机构运动学逆解:

$\begin{matrix} \begin{matrix} l_{i} = ‖ B_{i}^{1} - A_{i}^{1} ‖= f_{i} (α_{1}, β_{1}, z_{1}) = \\ F_{i} (x, y, z, α, β, γ) \\ i = 1, 2, 3, 4 \end{matrix} \end{matrix}$ (10)

同理, 对于3-PPR平面调整机构, D_i在局部坐标系O₄中位置矢量 $\begin{matrix} D_{i}^{4} \end{matrix}$ = $\begin{matrix} {(\begin{matrix} D_{ix}^{4} & D_{iy}^{4} & D_{iz}^{4} \end{matrix})}^{T} \end{matrix}$ 以及C_i在局部坐标系O₃中初始位置矢量 $\begin{matrix} C_{i 0}^{3} \end{matrix}$ = $\begin{matrix} {(\begin{matrix} C_{ix 0}^{3} & C_{iy 0}^{3} & C_{iz 0}^{3} \end{matrix})}^{T} \end{matrix}$ 同样可以由几何关系直接得出, 通过坐标变换可以求得D_i在局部坐标系O₃中位置矢量:

$\begin{matrix} D_{i}^{3} =_{4}^{3} R D_{i}^{4} + P_{O 4}^{3} (11) \end{matrix}$

由设计制造关系可知, C₁、C₃分别与D₁、D₃在Y₃向的坐标值相等, C₂与D₂在X₃向的坐标值相等, 从而解算得平面调整机构运动学逆解:

$\{\begin{matrix} l_{5} = D_{1 x}^{4} \sin γ_{1} + D_{1 y}^{4} \cos γ_{1} + y_{1} - C_{1 y 0}^{3} \\ l_{6} = D_{2 x}^{4} \cos γ_{1} - D_{2 y}^{4} \sin γ_{1} + x_{1} - C_{2 x 0}^{3} \\ l_{7} = D_{3 x}^{4} \sin γ_{1} + D_{3 y}^{4} \cos γ_{1} + y_{1} - C_{3 y 0}^{3} \end{matrix}$ (12)

亦即：

$l_{i} = f_{i} (x_{1}, y_{1}, γ_{1}) = F_{i} (x, y, z, α, β, γ) i = 5, 6, 7$ （13）

综合式(10)(13)即可得到系统运动学逆解:

$l_{i} = F_{i} (x, y, z, α, β, γ) i = 1, 2, \dots, 7$ （14）

3 BP神经网络运动学正解

BP神经网络是人工建立的以有向图为拓扑结构的动态系统, 可以实现从输入到输出的任意非线性映射。由于BP神经网络采用了全局逼近的方法, 并且具有很好的泛化能力, 因此很适合混联机构运动学正解的分析。

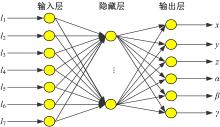
	Figure Option View Download New Window
	图3 六输出BP神经网络结构简图Fig.3 BP neural network with six outputs

单就神经网络而言, 多层神经网络的预测精度比单层更准确, 但耗时较长, 确定具体结构也相对复杂^[19]。因此本文采用单层神经网络结构, 以系统7个驱动位移量作为输入, 以LRU模块位姿对应的6个参数作为输出, 构建如图3所示“ 同输入, 同输出” 神经网络。为保证预测精度, 需要合理设计神经网络的结构参数。经过反复试验表明, 分别采用tangent sigmoid、purelin函数作为隐含层和输出层的激活函数, L-M优化函数作为网络的训练函数时预测精度较好。而隐藏层节点数根据经验公式采用逐步增长法确定^[20], 实验表明, 当隐含层节点为8时预测精度最高。同时为取消各维数据间数量级差别, 避免神经网络产生较大误差, 数据样本按照式(15)进行归一化处理^[21]:

$x'_{k} = \frac{x_{k} - x_{\min}}{x_{\max} - x_{\min}}$ （15）

$\begin{matrix} \{\begin{matrix} - 150 mm < x < 150 mm \\ - 150 mm < y < 150 mm \\ 1200 mm < z < 3800 mm \\ - 3 ° < α < 3 ° \\ - 3 ° < β < 3 ° \\ - 15 ° < γ < 15 ° \end{matrix} \end{matrix}$ （16）

式中:x_k为样本实际值; x_min为样本中最小值; x_max为样本中最大值; x'_k为样本归一化后的数值。

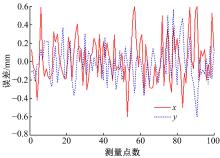
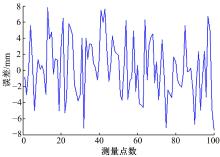
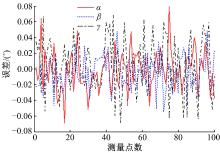
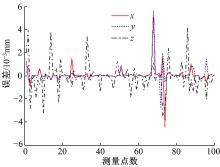
为防范不可预测工作空间的出现, 必须保证有足够的训练样本, 通过对不同数目样本下的预测精度进行对比, 发现2000组样本基本可以完成对工作空间的覆盖。因此, 在系统工作空间范围内随机生成2000组模块位姿参数(x, y, z, α , β , γ )作为网络的输出。根据装校平台实际设计制造尺寸及工程设计任务书要求, 各自由度可达工作空间满足约束条件(16)。通过运动学逆解求解对应位姿的各个驱动位移量(l₁, l₂, l₃, l₄, l₅, l₆, l₇)作为网络的输入, 从而构建网络的映射样本。在完成网络的训练后, 同理生成100组测试样本用于验证运动学正解误差, 所得位移及姿态角误差如图4、图5和图6所示。

	Figure Option View Download New Window
	图4 x、y向位移误差Fig.4 Displacement errors of x and y

	Figure Option View Download New Window
	图5 z向位移误差Fig.5 Displacement error of z

	Figure Option View Download New Window
	图6 姿态角误差Fig.6 Attitude angle errors

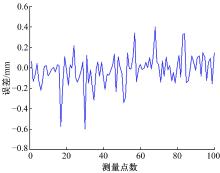
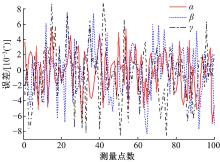
由以上误差数据分析可知, 位移和姿态角两类参数计算精度有所不同, 这表明这两类参数在对网络的非线性映射上存在差异, 同时位移参数中由于各向位移取值范围不同, 使得其精度也存在差异。因此, 采用“ 同输入, 单一输出” 的方法重新设计神经网络, 分别实现对单个自由度的求解, 即对应6个位姿参数设计6层子网络, 网络结构如图7所示, 所得位移及姿态角误差如图8~图10所示。

	Figure Option View Download New Window
	图7 单一输出BP神经网络结构简图Fig.7 BP neural network with single output

	Figure Option View Download New Window
	图8 子网络x、y向位移误差Fig.8 Errors of x and y within sub-network

	Figure Option View Download New Window
	图9 子网络z向位移误差Fig.9 Error of z within sub-network

	Figure Option View Download New Window
	图10 子网络姿态角误差Fig.10 Attitude angle errors within sub-network

分析可知, “ 同输入, 单一输出” 神经网络并未能解决不同类自由度以及各类自由度取值范围的不同对求解精度的影响, 但相对“ 同输入, 同输出” 神经网络而言其求解精度更高, 相应自由度求解精度均提高了一个数量级, 其中姿态角精度已达到10^-3(° )级, 而位移精度仍有待提高, 这也表明BP神经网络对复杂的非线性系统的预测精度有限, 其逼近能力存在一定局限性。

4 改进型BP神经网络运动学正解

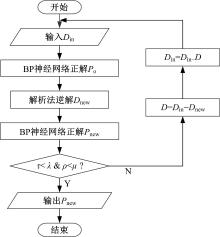
通过“ 同输入, 单一输出” 重新设计神经网络后, 姿态角精度已达10^-3mm级, 满足工程应用的要求, 因此只需进一步提高位移的求解精度。为此, 本文提出一种基于位置补偿的算法对神经网络进行改进, 以期降低位移自由度的计算误差, 该算法流程如图11所示。

	Figure Option View Download New Window
	图11 改进型算法流程图Fig.11 Flow chart of improved algorithm

τ = $\begin{matrix} \sqrt[]{{(x' - x)}^{2} + {(y' - y)}^{2} + {(z' - z)}^{2}} \end{matrix}$ (17)

ρ = $\begin{matrix} \sqrt[]{\overset{7}{\sum_{i = 1}} {(l'_{i} - l_{i})}^{2}} \end{matrix}$ (18)

式中:(x', y', z')为利用改进型神经网络解算所得位置坐标; l'_i为所对应驱动位移量。

图11中, λ 和μ 为目标误差, 当位置误差τ 和驱动误差ρ 达到设定目标误差时, 即τ < λ 、ρ < μ , 则直接输出位姿P_new; 若不满足条件, 则计算驱动位移量偏差D, 并进行补偿获得新的输入D_in, 循环往复该过程, 直至满足目标误差要求。由图12可知, 经过改进的BP神经网络, 其位移精度得到有效提高, 精度达到10^-3 mm级, 满足工程应用的精度要求。

	Figure Option View Download New Window
	图12 位移误差Fig.12 Displacement errors

5 结束语

针对神光-Ⅲ 激光装置LRU装校需要, 研制了一套具有6自由度精密调整功能的混联装校机构。以各姿态调整机构位姿为中间变量构建系统运动学逆解模型, 降低了系统运动学逆解的求解难度, 所得逆解结果为解析值, 无理论误差。以“ 同输入, 单一输出” 设计神经网络, 有效提高了运动学正解精度。基于位置补偿算法对神经网络进行改进, 使位移运动学正解精度达到工程应用要求。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	倪卫, 熊迁, 谭宁, 等. 神光-III主机装置下装模块空间对接关键技术[J]. 强激光与粒子束, 2013, 25(12): 3185-3188. Ni Wei, Xiong Qian, Tan Ning, et al. Key techniques of on-orbit docking for LRU of SG-III[J]. High Power Laser and Particle Beams, 2013, 25(12): 3185-3188. [本文引用:1]
[2]	吴小勇, 谢志江, 宋代平, 等. 基于改进蚁群算法的3-PPR并联机构位置正解研究[J]. 农业机械学报, 2015, 46(7): 339-344. Wu Xiao-yong, Xie Zhi-jiang, Song Dai-ping, et al. Forward kinematics of 3-PPR parallel mechanism based on improved ant colony algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(7): 339-344. [本文引用:1]
[3]	郭希娟, 张涛, 王玉镇, 等. 一种共轴混联机构的运动学分析[J]. 机械工程学报, 2014, 50(11): 60-67. Guo Xi-juan, Zhang Tao, Wang Yu-zhen, et al. Kinematic analysis of a new coaxial hybrid mechanism[J]. Journal of Mechanical Engineering, 2014, 50(11): 60-67. [本文引用:1]
[4]	Kanaan D, Wenger P, Chablat D. Kinematic analysis of a serial—parallel machine tool: the VERNE machine[J]. Mechanism and Machine Theory, 2009, 44(2): 487-498. [本文引用:1]
[5]	王瑞, 刘文涛, 纪校娟. 一种5轴混联加工中心的位姿正逆解分析[J]. 哈尔滨工业大学学报, 2010, 42(1): 128-132. Wang Rui, Liu Wen-tao, Ji Xiao-juan. Forward and inverse solution about a 5-axis serial-parallel machine tool[J]. Journal of Harbin Institute of Technology, 2010, 42(1): 128-132. [本文引用:1]
[6]	Tanev T K. Kinematics of a hybrid (parallel-serial) robot manipulator[J]. Mechanism and Machine Theory, 2000, 35(9): 1183-1196. [本文引用:1]
[7]	孙涛, 宋轶民, 李永刚, 等. 一类四自由度混联可重构主模块的全域静刚度预估[J]. 天津大学学报, 2010, 43(11): 1003-1008. Sun Tao, Song Yi-min, Li Yong-gang, et al. Global stiffness estimation of 4-DoF hybrid and reconfigurable module[J]. Journal of Tianjin University, 2010, 43(11): 1003-1008. [本文引用:1]
[8]	Gherman B, Pisla D, Vaida C, et al. Development of inverse dynamic model for a surgical hybrid parallel robot with equivalent lumped masses[J]. Robotics and Computer-Integrated Manufacturing, 2012, 28(3): 402-415. [本文引用:1]
[9]	Ibrahim O, Khalil W. Inverse and direct dynamic models of hybrid robots[J]. Mechanism and Machine Theory, 2010, 45(4): 627-640. [本文引用:1]
[10]	Campos A, Budde C, Hesselbach J. A type synthesismethod for hybrid robot structures[J]. Mechanism and Machine Theory, 2008, 43(8): 984-995. [本文引用:1]
[11]	Zeng Q, Fang Y. Structural synthesis and analysis of serial-parallel hybrid mechanisms with spatial multi-loop kinematic chains[J]. Mechanism and Machine Theory, 2012, 49(3): 198-215. [本文引用:1]
[12]	Wang Y, Pessi P, Wu H, et al. Accuracy analysis of hybrid parallel robot for the assembling of ITER[J]. Fusion Engineering and Design, 2009, 84(7-11): 1964-1968. [本文引用:1]
[13]	潘伯钊, 宋轶民, 王攀峰, 等. 基于激光跟踪仪的混联机器人快速零点标定方法[J]. 机械工程学报, 2014, 50(1): 31-37. Pan Bo-zhao, Song Yi-min, Wang Pan-feng, et al. Laser tracker based rapid home position calibration of a hybrid robot[J]. Journal of Mechanical Engineering, 2014, 50(1): 31-37. [本文引用:1]
[14]	Gallardo-Alvarado J, Posadas-García J D D. Mobility analysis and kinematics of the semi-general 2(3-RPS) series-parallel manipulator[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(6): 463-472. [本文引用:1]
[15]	罗华, 徐建柱, 姚林, 等. 可满足微创手术灵活工作空间的混联机器人研究[J]. 四川大学学报: 工程科学版, 2011, 43(4): 236-240. Luo Hua, Xu Jian-zhu, Yao Lin, et al. Study on hybrid robot meeting the dexterous workspace demand of minimally invasive surgery[J]. Journal of Sichuan University (Engineering Science Edition), 2011, 43(4): 236-240. [本文引用:1]
[16]	陈小立, 严宏志, 温广旭. 基于遗传算法的四自由度混联机器人轨迹规划[J]. 计算机仿真, 2014, 31(5): 346-350. Chen Xiao-li, Yan Hong-zhi, Wen Guang-xu. Trajectory planning of four DOF hybrid robot based on genetic algorithm[J]. Computer Simulation, 2014, 31(5): 346-350. [本文引用:1]
[17]	史家顺, 王凯, 朱立达, 等. 基于Clipper的3-TPS混联机器人运动轨迹控制[J]. 东北大学学报: 自然科学版, 2014, 35(10): 1512-1515. Shi Jia-shun, Wang Kai, Zhu Li-da, et al. Trajectory Control of 3-TPS hybrid robot based on clipper controller[J]. Journal of Northeastern University(Natural Science), 2014, 35(10): 1512-1515. [本文引用:1]
[18]	蔡自兴. 机器人学[M]. 北京: 清华大学出版社, 2009: 20-25. [本文引用:1]
[19]	杨永刚, 赵杰, 刘玉斌, 等. 6-PRRS并联机器人正运动学求解[J]. 吉林大学学报: 工学版, 2008, 38(3): 731-734. Yang Yong-gang, Zhao Jie, Liu Yu-bin, et al. Solving forward kinematics of 6-PRRS parallel robot[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(3): 731-734. [本文引用:1]
[20]	马立, 于瀛洁, 程维明, 等. BP神经网络补偿并联机器人定位误差[J]. 光学精密工程, 2008, 16(5): 878-883. Ma Li, Yu Ying-jie, Cheng Wei-ming, et al. Positioning error compensation for a parallel robot-based on BP neural networks[J]. Optics and Precision Engineering, 2008, 16(5): 878-883. [本文引用:1]
[21]	王小川, 史峰, 郁磊, 等. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013: 4-8. [本文引用:1]

2013

0.0

. 2013, 25(12):3185-3188 DOI:3185

Key techniques of on-orbit docking for LRU of SG-III

神光-III主机装置下装模块空间对接关键技术

Ni Wei , Xiong Qian , Tan Ning

倪卫, 熊迁, 谭宁

(Research Center of Laser Fusion, CAEP, P. O. Box 919-985, Mianyang 621900, China)

This essay analyzes the docking of line-replaceable unit (LRU) for some huge laser facilities, where centering and collision issues are pointed out as the key technologies for LRU docking monitoring. The centering technology mainly transforms the three-dimensional problem into two-dimensional one, adopting the characteristic of machine version capturing to analyze the position and posture of LRU. The collision monitoring technology mainly takes advantage of the principle that power is generated in the collision during the process of assembly and calibration. Monitoring force in all directions on the point of collision occurred, which indirectly reflects the degree of the collision, returning feedback to the docking platform after measurement data is analyzed, and amending the docking trajectory of the LRU in time can achieve the light collision docking during the full process of LRU.

初步分析了在建神光-Ⅲ主机装置下装模块空间对接过程，指出“对中”和“碰撞”问题是下装模块空间对接监测的关键技术。“对中”监测技术主要是将三维问题转换为二维问题，利用机器视觉扑捉特征点下装模块进行位置和姿态的判断。“碰撞”监测技术主要是利用下装模块装校过程发生碰撞必然产生“力”的作用的原理，监测碰撞点上各个方向作用力，间接反映碰撞发生程度，并将测量数据分析后反馈至对接平台执行，及时修正下装模块空间对接运动轨迹，实现了下装模块全过程的“轻碰撞”对接。

... 神光-III激光装置是我国目前功率最高、能量最大、最先进的ICF装置^[1],在其光学回路中安装有一系列不同规则的光机模块,这类光机模块称为在线可替换单元(LRU) ...

2015

0.0

. 2015, 46(7):339-344

Forward kinematics of 3-PPR parallel mechanism based on improved ant colony algorithm

基于改进蚁群算法的3-PPR并联机构位置正解研究

Wu Xiao-yong , Xie Zhi-jiang , Song Dai-ping

吴小勇, 谢志江, 宋代平

... 基于LRU模块制造精密、造价昂贵、洁净度高、质量大等原因,在装校和拆卸LRU模块时需要一套可实现6自由度精密调整的装校平台^[2],该装校平台主要由水平调整机构、升沉机构以及平面调整机构混联组成 ...

2014

0.0

. 2014, 50(11):60-67 DOI:doi:10.3901/JME.2014.11.060

Kinematic analysis of a new coaxial hybrid mechanism

一种共轴混联机构的运动学分析

Guo Xi-juan , Zhang Tao , Wang Yu-zhen

郭希娟, 张涛, 王玉镇

给出一种新型共轴混联机构,该机构由一个并联机构与一个混联机构同轴反方向旋转构成,其特点是机构反向旋转的两个动环并不直接接触,高速旋转时的稳定性高.分析该机构的运动学特性,对机构进行位置分析,计算机构的自由度,建立运动学反解方程,采用直接求导法,计算机构的速度、加速度.为了能够更加直观地观察计算结果,选择正弦函数作为末端变化函数,来观察各支链的运动轨迹以及速度加速度的变化.

... 混联机构作为串联机构和并联机构的结合体,既克服了并联机构工作空间小、运动不灵活的缺点,又解决了串联机构精度、刚度及实时控制方面的不足,兼具并联机构刚度大和串联机构工作空间大的优点,是机构学重要的研究方向之一^[3] ...

2009

0.0

... Kanaan等^[4]研制了一台5轴混联机床,并对其运动学正逆解进行了研究 ...

2010

0.0

. 2010, 42(1):128-132 DOI:doi:10.11918/j.issn.0367-6234.2010.01.030

Forward and inverse solution about a 5-axis serial-parallel machine tool

一种5轴混联加工中心的位姿正逆解分析

Wang Rui , Liu Wen-tao , Ji Xiao-juan.

王瑞, 刘文涛, 纪校娟

To resolve some problems,such as small workspace,about the traditional parallel machine tools,a new kind of 5-axis serial-parallel machine tool is introduced,which has large workspace as well as good static and dynamic stiffness.Considering the strong coupling between position parameters and orientation parameters of the movable platform,the relationship between them is established.The numerical and analytic algorithms are adopted together to solve the inverse kinematics solution,and the bar length approaching algorithm is adopted in the forward kinematics solution without consideration of the additional initial position parameters.The solution method is verified to be correct through two samples,which is important to the analysis of control system of the machine tool.

为了解决目前纯并联机床存在的问题,研究了一种新型5轴混联加工中心结构,该新型结构具有工作空间大、静动态刚度好的优点.针对其运动参数间存在较强的耦合性,给出了运动平台姿态参数与位置参数间的数学解耦关系,将解析法和数值法相结合,对其位姿逆解进行了详细的推导,同时借助改进的杆长逼近法,进行了位姿正解的推导.实例验证结果表明算法正确、有效.该算法对混联机构的运动分析具有一定的参考意义.

... 王瑞等^[5]设计了一种新型混联加工中心,结合解析法和数值法对其位姿正逆解进行了分析 ...

2000

0.0

... Tanev^[6]运用封闭解法研究了一种新型混联机构的运动学特性 ...

2010

0.0

. 2010, 43(11):1003-1008 DOI:doi:10.3969/j.issn.0493-2137.2010.11.010

Global stiffness estimation of 4-DoF hybrid and reconfigurable module

一类四自由度混联可重构主模块的全域静刚度预估

Sun Tao , Song Yi-min , Li Yong-gang

孙涛, 宋轶民, 李永刚

为满足国家飞机、汽车等零部件制造作业需求,提出了一种混联可重构机械手,与同体积的Tricept机械手相比,该机械手能实现更大的工作空间,对其四自由度混联主模块的关键设计指标--静刚度进行了研究.考虑到主模块的拓扑构型为混联形式,将主模块划分为并联子系统和串联子系统.在利用虚功原理和子结构综合思想分别建立并联和串联子系统静刚度解析模型的基础上,借助线性叠加原理构造了球坐标系下主模块的整体静刚度解析模型.借助三维造型和有限元商用软件对主模块进行了建模和有限元分析,验证了该主模块整机静刚度解析模型的有效性,并结合算例对四自由度混联主模块的静刚度进行了全域预估.研究结果为研制具有我国自主知识产权的并/混联构型装备提供了理论依据.

... 孙涛等^[7]发明了一种混联可重构机械手,针对其静刚度进行了全域预估 ...

2012

0.0

... Gherman等^[8]建立了PARASURG-5M混联医疗机器人动力学逆解模型,并用于该机构的动力控制 ...

2010

0.0

... Ibrahim等^[9]采用递归法研究了Logabex LX4混联机器人的动力学特性 ...

2008

0.0

... Campos等^[10]基于阿苏尔杆组法剖析了混联机构的型综合问题 ...

2012

0.0

... Zeng等^[11]运用群论对混联机构进行了构型分析 ...

2009

0.0

... Wang等^[12]对一种移动冗余混联机器人进行了误差补偿 ...

2014

0.0

. 2014, 50(1):31-37

Laser tracker based rapid home position calibration of a hybrid robot

基于激光跟踪仪的混联机器人快速零点标定方法

Pan Bo-zhao , Song Yi-min , Wang Pan-feng

潘伯钊, 宋轶民, 王攀峰

... 针对EXE-M混联机器人,潘伯钊等^[13]提出了基于激光跟踪仪的快速零点标定技术 ...

2013

0.0

... Gallardo-Alvarado^[14]、罗华^[15]等分析了混联机构的灵巧度,陈小立^[16]、史家顺^[17]等则用不同的算法对相应混联机器人进行了轨迹规划 ...

2011

0.0

. 2011, 43(4):236-240

Study on hybrid robot meeting the dexterous workspace demand of minimally invasive surgery

可满足微创手术灵活工作空间的混联机器人研究

Luo Hua , Xu Jian-zhu , Yao Lin

罗华, 徐建柱, 姚林

摘　要：针对微创手术对机器人提出的高灵活性要求,设计出一种具有混联结构的微创外科手术机器人,并通过灵活工作空间分析进行结构优化,为合理布置手术切口及规划手术路径,利用末端手术工具服务球和服务区进行工作空间灵活性分析,通过数值解得到混联机器人工作空间内任意点的灵活度,并绘制出工作空间水平截面灵活性分布图,为手术切口位置和工具杆末端运动路径提供工作数据;再以工作空间水平截面灵活度大于0.85的灵活点数目作为评价指标,定量分析了姿态机构腕关节转角范围及手术工具杆长度对灵活性的影响,为微创外科混联机器人的结构优化提供了计算依据。仿真对比和优化后的实物实际运动结果均证明了该混联机器人可满足微创手术的灵活性要求。

... Gallardo-Alvarado^[14]、罗华^[15]等分析了混联机构的灵巧度,陈小立^[16]、史家顺^[17]等则用不同的算法对相应混联机器人进行了轨迹规划 ...

2014

0.0

. 2014, 31(5):346-350 DOI:doi:10.3969/j.issn.1006-9348.2014.05.079

Trajectory planning of four DOF hybrid robot based on genetic algorithm

基于遗传算法的四自由度混联机器人轨迹规划

Chen Xiao-li , Yan Hong-zhi , Wen Guang-xu.

陈小立, 严宏志, 温广旭

研究机器人轨迹优化控制问题,为了兼顾机器人高速运动的平稳性与工作效率,以四自由度混联机器人为研究对象,提出了一种基于遗传算法的轨迹规划方案。运用坐标变换法建立混联机器人的运动学模型;在考虑机器人位置、速度、加速度约束的基础上,采用"3-5-3"法在关节空间对机器人进行轨迹规划。通过遗传算法对各路径点间的时间间隔进行最优规划,获得各关节的位置、速度、加速度轨迹图像。仿真结果表明,所设计的方案能保证机器人运行时间最优以及轨迹连续平滑。

... Gallardo-Alvarado^[14]、罗华^[15]等分析了混联机构的灵巧度,陈小立^[16]、史家顺^[17]等则用不同的算法对相应混联机器人进行了轨迹规划 ...

2014

0.0

. 2014, 35(10):1512-1515

Trajectory Control of 3-TPS hybrid robot based on clipper controller

基于Clipper的3-TPS混联机器人运动轨迹控制

Shi Jia-shun , Wang Kai , Zhu Li-da

史家顺, 王凯, 朱立达

... Gallardo-Alvarado^[14]、罗华^[15]等分析了混联机构的灵巧度,陈小立^[16]、史家顺^[17]等则用不同的算法对相应混联机器人进行了轨迹规划 ...

2009

0.0

... ₁)分别为绕x、y、z轴的旋转变换矩阵^[18] ...

2008

0.0

. 2008, 38(3):731-734

Solving forward kinematics of 6-PRRS parallel robot

6-PRRS并联机器人正运动学求解

Yang Yong-gang , Zhao Jie , Liu Yu-bin

杨永刚, 赵杰, 刘玉斌

... 单就神经网络而言,多层神经网络的预测精度比单层更准确,但耗时较长,确定具体结构也相对复杂^[19] ...

2008

0.0

. 2008, 16(5):878-883 DOI:doi:10.3321/j.issn:1004-924X.2008.05.019

Positioning error compensation for a parallel robot-based on BP neural networks

BP神经网络补偿并联机器人定位误差

Ma Li , Yu Ying-jie , Cheng Wei-ming

马立, 于瀛洁, 程维明

In order to reduce mechanism end errors and enhance robot motion accuracy，the main error sources of the parallel robot and the limitations of conventional error compensation are discussed for the 6-DOF precision parallel robot designed. An error compensation method based on back propagation (BP) neural networks of articulatory space, by measuring the end pose, is presented in local workspace of precision positioning. Model of BP Network and data sample of error compensation are established, and the data sample is standardized. By the experiment, the node number of hidden layer is achieved. In order to improvement the generalization performance, the overfitting is prevented in the network training. After error compensation, the positioning error and the orientation error reduce by 80% and 60% respectively. The experimental results show that the error compensation, based on BP neural networks of articulatory space, has an obvious effect, which satisfies the accuracy requirements of the precision parallel robot.

为减小机构末端定位误差，提高机器人运动精度，分析了所开发的6-DOF精密并联机器人末端位姿的误差来源及以往误差补偿方法的局限性。通过实际测量末端位姿，在精密定位的局部工作空间内，提出了基于BP神经网络的机器人关节空间误差补偿方法。确定了BP神经网络模型，建立了误差补偿的数据样本，并对数据样本进行了标准化，通过实验对比的方法确定了隐层神经元的个数，同时对网络的推广能力进行了验证。经过误差补偿，6-DOF精密并联机器人的平移定位误差下降了80%，转角定位误差下降了60%。该实验结果表明，基于BP神经网络的误差补偿方法对机器人局部工作空间的补偿具有明显的效果，满足精密并联机器人工作的精度要求。

... 而隐藏层节点数根据经验公式采用逐步增长法确定^[20],实验表明,当隐含层节点为8时预测精度最高 ...

2013

0.0

... 同时为取消各维数据间数量级差别,避免神经网络产生较大误差,数据样本按照式(15)进行归一化处理^[21]: ...