最小故障率下数控组合机床平均维修时间确定

引用本文

申桂香, 曾文彬, 张英芝, 吴茂坤, 郑玉彬. 最小故障率下数控组合机床平均维修时间确定. 吉林大学学报（工学版）, 2017, 47(5): 1519-1526
SHEN Gui-xiang, ZENG Wen-bin, ZHANG Ying-zhi, WU Mao-kun, ZHENG Yu-bin. Determination of average maintenance time of CNC machine tools under minimum failure rate. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1519-1526 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705025
Permissions

最小故障率下数控组合机床平均维修时间确定

申桂香, 曾文彬, 张英芝, 吴茂坤, 郑玉彬

吉林大学机械科学与工程学院,长春 130022

通信作者:张英芝(1970-),女,副教授,博士.研究方向:数控机床可靠性.E-mail:zhangyz@jlu.edu.cn

作者简介:申桂香(1957-),女,教授,博士生导师.研究方向:数控装备及其全生命周期工程.E-mail:shengx@jlu.edu.cn

基金项目:国家科技重大专项项目(2015ZX04003002); 吉林省科技发展计划项目(20150101025JC)

摘要

为合理计算数控组合机床整机平均维修时间,本文提出基于系统组件故障率和维修时间模型来确定系统平均维修时间的方法。根据数控组合机床子系统故障信息,引入平均秩次法进行基于时间相关的子系统故障率建模,进而实现数控组合机床系统故障率建模。结合各子系统维修时间函数,建立了数控组合机床整机平均维修时间模型,并确定了最小故障次数下的整机平均维修时间。本文研究为系统维修时间设计及维修计划制定奠定了理论基础。

关键词: 机床; 平均维修时间; 最小故障率; Johnson法

中图分类号:TG659 文献标志码:A 文章编号:1671-5497(2017)05-1519-08

Determination of average maintenance time of CNC machine tools under minimum failure rate

SHEN Gui-xiang, ZENG Wen-bin, ZHANG Ying-zhi, WU Mao-kun, ZHENG Yu-bin

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

In order to reasonably compute the average maintenance time of combination of CNC machine tools, a calculation method of the average maintenance time is developed based on the system component failure rate and maintenance time model. First, according to the subsystem fault information of the combination of CNC machine, the mean rank method is introduced to establish the time related subsystem failure rate model. Then the system failure rate model of the combination of CNC machine tools is derived. Finally, combining the subsystem maintenance time function, the average maintenance time model of the combination of CNC machine tools is established, and the average maintenance time is determined by the minimum number of failures. This research may provide reference for system maintenance time design and maintenance planning.

Key words: machine tool; average maintenance time; minimum failure rate; Johnson method

Show Figures

0 引言

有统计表明^[1], 数控组合机床维修保养费用在整个寿命周期费用中的占比高达20%~30%。因此, 进行整机维修时间研究对于合理选择维修策略、制定维修计划, 保证企业生产的可持续性、减少企业停机维修损失等有重要意义。

目前, 国内外对于维修策略的研究主要集中于维修模型的研究, 且主要基于成本与可靠性为约束展开。Dale等^[2]建立了以可靠性为约束条件维修费用最小维修计划优化模型。成国庆等^[3]针对工程技术领域中的串联可修系统, 以系统中部件的故障次数为更换策略, 系统平均费用率为目标函数, 提出了一种维修更换模型。申桂香等^[4]在有效性最大的基础上, 提出一种在修复型维修状态下的最佳预防维修间隔时间模型, 最大限度保证机床的使用性能并减少维修费用。石慧等^[5]提出一种基于复杂系统剩余寿命有效预测的预防性维护维修策略, 其优化模型的目标函数是最小化平均维护费用。程志君等^[6]针对部件间存在经济相关性的复杂系统, 提出一类基于机会策略的视情维修优化模型。通过对比发现, 应用模型能够降低系统的运行维护费用, 如果部件级失效率之比在适当范围内, 其经济相关性越强, 节省费用的效率越高。蔡景等^[7]以故障风险为约束, 以系统总体维修费用最小化、系统利用率最大化为目标, 建立了复杂系统成组维修策略的优化模型。李剑涛等^[8]从装备的可靠性和维修费用出发, 重点研究了年龄维修策略的维修间隔期和定期检测策略的检测时间间隔的定量分析方法。

系统维修时间与组件故障率及维修时间密切相关, 是组件故障率及其维修时间的函数。但目前系统预防维修时间或平均维修时间的确定大多忽略系统组件的故障率及各组件维修时间, 而是将其所有组件维修时间不加区分统一放在一起, 通过模型假设、参数估计及假设检验确定其分布模型进而通过点估计得到。该计算得到的系统平均维修时间存在较大误差, 使得据此制定的维修周期计划不符合工程实际, 影响维修效果。因此, 本文将考虑系统组件的故障时间相关性, 建立基于故障时间相关的组件故障率模型^[9], 结合各组件维修时间模型, 建立基于组件平均维修时间加权的系统平均维修时间模型以确定最小故障次数下系统平均维修时间。以数控组合机床为例介绍具体计算过程, 为实现系统维修时间设计及维修计划制定提供理论依据。

1 系统平均维修时间建模原理

首先, 建立时间相关下系统组件故障率模型; 然后, 依据系统组件串联关系建立系统故障率模型并确定系统最小故障率值; 最后, 结合各组件维修时间模型建立最小故障率下系统平均维修时间模型。

1.1 基于时间相关的系统组件可靠性建模

综合考虑系统其余组件故障时间和定时截尾可靠性试验等多重截尾数据对系统组件故障时间的影响, 引入平均秩次法对故障时间次序进行修正, 应用近似中位秩法建立经验分布函数, 采用极大似然估计法(MLE)法进行参数估计, 采用d检验法进行模型拟合性检验, 以确定各系统组件可靠性函数^[10]。

(1)系统组件故障秩次修正

为节约试验时间和费用, 数控组合机床可靠性试验采用定时截尾方式进行, 因此, 试验结束时每台试验机床会产生一个截尾数据(验截止时间与最后一个试验时间之差)。同时, 当系统故障时, 一个组件会产生一个自身的故障时间并使得系统所有其他组件的时间截尾。因为多重截尾数据的存在, 致使被研究组件的故障次序发生变化, 为此, 本文采用Johnson法^[8], 引入秩增量来修正这一秩次变动。

系统任一组件A第i个故障数据的秩增量 $\begin{matrix} A_{Δ t_{i}} \end{matrix}$ 按下式计算:

$\begin{matrix} A_{Δ t_{i}} = \frac{N + 1 - A_{t_{(i - 1)}}}{N + 2 - j} \end{matrix}$ （1）

式中: $\begin{matrix} A_{t_{(i - 1)}} \end{matrix}$ 为组件A第i-1个故障数据秩次, i=1, 2, …, n, 定义 $\begin{matrix} A_{t_{(0)}} \end{matrix}$ =0; N为故障数据与截尾数据总数; j为N个故障数据从小至大的排列秩次, j=1, 2, …, N。

组件A的第i个故障数据的秩次为:

$\begin{matrix} A_{t_{i}} = A_{t_{(i - 1)}} + A_{Δ t_{i}} = A_{t_{(i - 1)}} + \frac{N + 1 - A_{t_{(i - 1)}}}{N + 2 - j} \end{matrix}$ （2）

修正后的数控组合机床的故障分布函数F(t_i)的经验值按近似中位秩法计算, 公式为:

$\begin{matrix} F (t_{i}) \approx \frac{A_{t_{i}} - 0.3}{N + 0.4} \end{matrix}$ （3）

(2)参数估计与修正

本文以两参数威布尔分布为假设模型, 考虑到各系统组件样本量较少, 为提高参数估计精度, 本文采用极大似然估计法(MLE)进行模型参数估计。

设t₁, t₂, …, t_n为一组件故障间隔时间顺序统计量, 威布尔模型的形状参数和尺寸参数的极大似然估计 $\begin{matrix} \hat{β} \end{matrix}$ 和尺寸参数 $\begin{matrix} \hat{α} \end{matrix}$ 满足以下方程:

$\frac{1}{\hat{β}} = \frac{\overset{n}{\sum_{i = 1}} t_{_{i}}^{\hat{β}} \ln t_{i}}{\overset{n}{\sum_{i = 1}} t_{_{i}}^{\hat{β}}} - \frac{1}{n} \overset{n}{\sum_{i = 1}} \ln t_{i}$ （4）

$\begin{matrix} \hat{α} = {(\frac{1}{n} \overset{n}{\sum_{i = 1}} t_{_{i}}^{\hat{β}})}^{1 / \hat{β}} \end{matrix}$ (5)

迭代算法为:

$\begin{matrix} \{\begin{matrix} {\hat{β}}_{k + 1} = \frac{1}{2} {\hat{β}}_{k} + \frac{1}{2} {[h ({\hat{β}}_{k}) - \bar{X}]}^{- 1} \\ {\hat{β}}_{0} = 1.0 \end{matrix} \end{matrix}$ (6)

式中: $\begin{matrix} \bar{X} \end{matrix}$ = $\begin{matrix} \frac{1}{n} \end{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix} \begin{matrix} t_{_{i}}^{{\hat{β}}_{k}} \end{matrix}$ ; h $\begin{matrix} ({\hat{β}}_{k}) \end{matrix}$ = $\begin{matrix} \frac{\overset{n}{\sum_{i = 1}} t_{_{i}}^{{\hat{β}}_{k}} \ln t_{i}}{\overset{n}{\sum_{i = 1}} t_{_{i}}^{{\hat{β}}_{k}}} \end{matrix}$ ; $\begin{matrix} {\hat{β}}_{k} \end{matrix}$ 为第k次迭代后求解到的 $\begin{matrix} \hat{β} \end{matrix}$ , 随迭代次数的递增, 其值接近最优解。

因系统组件故障数据个数较少, 属于小样本问题。使用MLE法得到的结果有一定偏差, 因此需要在参数估计结果的基础上进行偏差修正, 公式如下:

$\begin{matrix} β^{*} = γ_{β} (n) \hat{β} (7) \end{matrix}$

式中:γ _β $\begin{matrix} (n) \end{matrix}$ 为 $\begin{matrix} \hat{β} \end{matrix}$ 的修偏系数, 按下式计算:

$\begin{matrix} γ_{β} (n) = \{\begin{matrix} \frac{\sqrt[]{2} Γ (\frac{n - 1}{2})}{\sqrt[]{n} Γ (\frac{n}{2} - 1)}, n \geq 4 \\ \frac{\sqrt[]{2}}{\sqrt[]{3 π}}, n = 3 \end{matrix} \end{matrix}$ (8)

当n≥ 4, 且为偶数时, 有

$\begin{matrix} γ_{β} (n) = \sqrt[]{\frac{π}{n}} \times \frac{1 \times 3 \times 5 \times \dots \times (n - 3)}{2^{\frac{n - 3}{2}} (\frac{n}{2} - 2)!} \end{matrix}$ (9)

当n为大于等于5的奇数时, 有

$\begin{matrix} γ_{β} (n) = \frac{2^{\frac{n}{2} - 1}}{\sqrt[]{nπ}} \times \frac{(\frac{n - 3}{2})!}{1 \times 3 \times 5 \times \dots \times (n - 4)} \end{matrix}$ （10）

对于任意n≥ 3, 有γ _β $\begin{matrix} (n) \end{matrix}$ < 1, 且 $\begin{matrix} \lim_{n \to \infty} \end{matrix}$ γ _β $\begin{matrix} (n) \end{matrix}$ =1, 所以β ^*< $\begin{matrix} \hat{β} \end{matrix}$ , 用式(7)对形状参数β 进行偏差修正。

基于MLE的尺度参数α 的偏差修正公式为:

$\begin{matrix} α^{*} = γ_{α} (n, β^{*}) \hat{α} (11) \end{matrix}$

式中:γ _α $\begin{matrix} (n, β^{*}) \end{matrix}$ = $\begin{matrix} \frac{n^{\frac{1}{β^{*}}} (n - 1)!}{Γ (n + \frac{1}{β^{*}})} \end{matrix}$ 。

(3)假设检验

本文采用d检验法对系统组件故障间隔时间分布函数进行拟合优度检验。d检验法是将n个试验数据按由小到大的次序排列, 根据假设的分布, 计算每个数据对应的F₀(x_i), 将其与经验分布函数F_n(x_i)进行比较, 其中差值的最大绝对值即检验统计量D_n的观察值。将D_n与临界值D_n_,_α进行比较。满足下列条件, 则接受原假设, 否则拒绝原假设。

$\begin{matrix} D_{n} = \sup_{- \infty < x < + \infty} |F_{n} (t_{i}) - F_{0} (t_{i})| = \max \{d_{i}\} < D_{n, α} \end{matrix}$ (12)

式中:D_n_,_α为临界值; F₀ $\begin{matrix} (x) \end{matrix}$ 为原假设分布函数; F_n $\begin{matrix} (x) \end{matrix}$ 为样本大小为n的经验分布函数, 即

$\begin{matrix} F_{n} (x) = \{\begin{matrix} 0, x < x_{i} \\ \frac{r_{i} - 0.3}{n + 0.4}, \\ x_{i} < x < x_{i + 1}, x_{1} < x_{2} < \dots < x_{n} \\ 1, x \geq x_{n} \end{matrix} \end{matrix}$ （13）

1.2 基于小样本的系统组件维修时间建模

在系统组件维修性建模过程中, 考虑系统组件的小样本特点, 采用正态分布的小样本数据处理方法和粒子群优化算法进行参数优化估计, 确定其维修时间模型间, 计算各系统组件平均维修时间, 为后面考虑系统组件间故障相关性的维修时间计算提供基础。

故障维修时间τ 服从对数正态分布ln(μ , σ ²), 则其对数lnτ 服从正态分布N(μ , σ ²)。那么维修时间τ 的概率密度函数表达式为:

$\begin{matrix} m (τ) = \frac{1}{σt \sqrt[]{2 π}} \exp \{- \frac{1}{2} {(\frac{lnτ - μ}{σ})}^{2}\} \end{matrix}$ （14）

累积分布函数表达式为:

$\begin{matrix} M (τ) = \int_{0}^{τ} \frac{1}{σx \sqrt[]{2 π}} \exp \{- \frac{1}{2} {(\frac{lnx - μ}{σ})}^{2}\} dx \end{matrix}$ （15）

式中:σ 和μ 为待估参数。

对σ 和μ 进行参数估计。设样本τ ₁, τ ₂, …, τ _n是某个层级系统组件的维修时间数据, 对于样本τ _i处的维修概率估计值 $\begin{matrix} {\hat{p}}_{i} \end{matrix}$ :

$\begin{matrix} {\hat{p}}_{i} = t_{n - 1} (\sqrt[]{\frac{n}{n + 1}} \cdot \frac{X_{i} - \bar{X}}{S}) \end{matrix}$ （16）

式中:X_i=lnτ _i; $\begin{matrix} \bar{X} \end{matrix}$ = $\begin{matrix} \frac{1}{n} \end{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ lnτ _i; S= $\begin{matrix} \frac{1}{n - 1} \end{matrix}$ · $\begin{matrix} \sqrt[]{{(X_{i} - \bar{X})}^{2}} \end{matrix}$ 。

由于X_i=lnτ _i, 因此在得到维修概率估计值 $\begin{matrix} {\hat{p}}_{i} \end{matrix}$ 后, 进一步可以得到各个 $\begin{matrix} (τ_{i}, {\hat{p}}_{i}) \end{matrix}$ 点, 再结合最小二乘法可以得到该系统组件的维修性模型参数估计值。

最小二乘法的约束准则为:

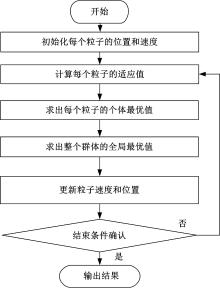
$Q = \overset{n}{\sum_{i = 1}} [\int_{0}^{τ_{i}} \frac{1}{σx \sqrt[]{2 π}} \cdot {\exp \{- \frac{1}{2} {(\frac{lnx - μ}{σ})}^{2}\} dx - {\hat{p}}_{i}]}^{2} = \min$ （17）

式(17)是在最小二乘法的约束准则下的参数优化问题, 可以使用粒子群优化算法(Particle swarm optimization, PSO)来求解。PSO优化算法的流程图如图1所示。

	Figure Option View Download New Window
	图1 PSO算法流程图Fig.1 Flow chart of PSO algorithm

1.3 最小故障率下系统平均维修时间建模

一个系统的维修时间可以表示成其组成零部件维修时间的函数, 因此, 可以通过计算其系统组件或部件的平均维修时间得到系统的平均维修时间。系统平均维修时间可以通过计算系统组件平

均维修时间的加权平均值得到, 加权系数的大小跟系统组件的故障次数相关。设MTTR_i为第i个系统组件的平均维修时间, f_i为第i个系统组件在系统设计寿命期内的故障次数, q_i为系统组件i的数量, 则系统平均维修时间为:

$\begin{matrix} MTTR = \frac{\overset{n}{\sum_{i = 1}} q_{i} f_{i} MTT R_{i}}{\overset{n}{\sum_{i = 1}} q_{i} f_{i}} \end{matrix}$ （18）

考虑到系统组件的故障次数与其故障率密切相关且所有部件使用时间相同, 加之考虑了系统组件间故障相关性的故障率, 使得加权系数更加准确合理, 故可以用λ _i代替f_i。若在一个设备里面, 系统组件划分都是唯一的, 则q_i=1, 进而系统平均维修时间可以改写为:

$\begin{matrix} MTTR = \frac{\overset{n}{\sum_{i = 1}} λ_{i} MTT R_{i}}{\overset{n}{\sum_{i = 1}} λ_{i}} \end{matrix}$ （19）

式中:λ _i为各层级系统组件故障率。

由式(19)可知, 该系统平均维修时间计算综合考虑了各个系统组件的故障率, 对不同系统组件赋予了相应的维修加权系数, 使得系统平均维修时间计算符合企业生产实际。

数控组合机床系统是各组件组成的串联系统, 依据各系统组件故障率函数λ _i(t), 得到数控组合机床系统故障率函数λ (t)为:

$\begin{matrix} λ (t) = \overset{n}{\sum_{i = 1}} λ_{i} (t) \end{matrix}$ (20)

依据Matlab编程可确定系统最小故障率时的时间 $\begin{matrix} t_{λ_{\min}} \end{matrix}$ , 进而求得此时各系统组件故障率λ _i $\begin{matrix} (t_{λ_{\min}}) \end{matrix}$ , 根据式(19)可得到系统最小故障率下系统平均维修时间为:

$\begin{matrix} MTTR (t_{λmin}) = \frac{\overset{n}{\sum_{i = 1}} λ_{i} (t_{λ_{\min}}) MTT R_{i}}{\overset{n}{\sum_{i = 1}} λ_{i} (t_{λ_{\min}})} \end{matrix}$ (21)

2 案例

2.1 数控组合机床系统组件划分

本文结合数控组合机床的主要结构以及工作过程, 应用模块化方法进行整机的功能系统划分, 具体如表1所示。

表1 数控组合机床子系统划分表 Table 1 Subsystem partition of numerical control combined machine tool

为简化计算过程, 进一步将其划分为3类组件, 具体如表2所示。

表2 数控组合机床组件划分 Table 2 Division of CNC machine tool components

2.2 数控组合机床子系统可靠性建模

课题组对5台采用定时截尾方式进行可靠性试验的数控组合机床进行为期6个月跟踪, 采集5台数控组合机床的现场运行故障数据28条, 试验截尾时间数据5条。如表3所示, 可以根据故障机理分析确定3类组件故障信息。

表3 三系统组件故障时间 Table 3 Failure time of three system component

表3中带“ * ” 的表示机械组件故障数据; 带“ #” 的表示辅助组件故障数据; 其余为电气组件故障数据。

本文以机械组件为例介绍建模过程, 依据式(3)对机械组件故障秩序进行修正, 如表4所示。

表4 机械组件故障秩序修正 Table 4 Fault order correction of mechanical component

j	i	t_i	$\begin{matrix} A_{t_{i}} \end{matrix}$	F(t_i)
2	1	15	1	0.0210
13	2	230	2.500	0.0659
19	3	336	4.469	0.1248
20	4	357	6.438	0.1813
24	5	511	8.944	0.2589
25	6	570	11.450	0.3338

表4 机械组件故障秩序修正 Table 4 Fault order correction of mechanical component

按式(4)进行迭代计算, 对机械组件的参数估计, 运行Matlab编程进行100次迭代。得到形状参数的估计值为:

$\begin{matrix} \hat{β} \end{matrix}$ =1.4893

再由式(5)可得尺度参数α 的估计值为:

$\begin{matrix} \hat{α} \end{matrix}$ =366.4572

同理, 可得其余两系统组件的参数估计值, 如表5所示。

表5 三系统组件可靠性模型参数估计值 Table 5 Reliability model parameter estimation of three system component

系统组件	$\begin{matrix} \hat{β} \end{matrix}$	$\begin{matrix} \hat{α} \end{matrix}$
机械组件	1.4893	366.4572
电气组件	1.0660	352.9860
辅助组件	0.9211	456.9429

表5 三系统组件可靠性模型参数估计值 Table 5 Reliability model parameter estimation of three system component

利用式(8)对3个系统组件威布尔分布的参数进行偏差修正, 整理得表6。

表6 三系统组件可靠性模型参数修正值 Table 6 Reliability model parameter correction value of three system component

对数控组合机床机械组件故障时间分布函数进行d检验, 得到拟合检验表, 如表7所示。

表7 机械组件拟合性检验表 Table 7 Fitting test of mechanical components

由表7可知, D_n的观察值为0.4969, 取显著性水平α =0.10, 查表D_n_,_α=1.22/ $\begin{matrix} \sqrt[]{6} \end{matrix}$ =0.498。由于D_n< D_n_,_α, 因此接受原假设, 模型通过了拟合优度检验, 数控组合机床机械组件故障时间服从威布尔分布。所以, 该型数控组合机床机械组件故障间隔时间的故障率函数λ ₁(t)为:

λ ₁ $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} \frac{f_{1} (t)}{R_{1} (t)} \end{matrix}$ = $\begin{matrix} \frac{1.1502}{379.0124} \end{matrix} \begin{matrix} {(\frac{t}{379.0124})}^{0.1502} \end{matrix}$

同理, 可得电气组件的故障率函数为:

λ ₂ $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} \frac{f_{2} (t)}{R_{2} (t)} \end{matrix}$ = $\begin{matrix} \frac{0.9615}{352.9758} \end{matrix} \begin{matrix} {(\frac{t}{352.9758})}^{- 0.0385} \end{matrix}$

辅助组件的故障率函数为:

λ ₃ $\begin{matrix} (t) \end{matrix}$ = $\begin{matrix} \frac{f_{3} (t)}{R_{3} (t)} \end{matrix}$ = $\begin{matrix} \frac{0.7821}{450.1370} \end{matrix} \begin{matrix} {(\frac{t}{450.1370})}^{- 0.2179} \end{matrix}$

2.3 数控组合机床子系统维修时间建模

5台数控组合机床的故障维修时间信息分析整理如表8所示。

表8 数控组合机床故障维修时间表 Table 8 Failure repair time of CNC machine tool

表格中, 带“ * ” 的为机械组件维修时间数据; 带“ #” 的为辅助组件维修时间数据; 其余为电气组件维修时间数据。

以机械组件为例, 对其维修时间进行建模。假设机械组件维修时间服从对数正态分布, 其参数估计如表9所示, 表中均值和方差分别为1.4256、1.003。

在得到机械组件样本各点(τ _i, $\begin{matrix} {\hat{p}}_{i} \end{matrix}$ )之后, 采用粒子群优化算法, 运用Matlab进行编程可以得到机械组件维修性模型的参数估计值 $\begin{matrix} {\hat{μ}}_{1} \end{matrix}$ =1.4031, $\begin{matrix} {\hat{σ}}_{1} \end{matrix}$ =0.9501。同理, 可得电气组件参数估计值 $\begin{matrix} {\hat{μ}}_{2} \end{matrix}$ =1.3548, $\begin{matrix} {\hat{σ}}_{2} \end{matrix}$ =0.5197; 辅助组件参数估计值 $\begin{matrix} {\hat{μ}}_{3} \end{matrix}$ =1.3349, $\begin{matrix} {\hat{σ}}_{3} \end{matrix}$ =1.1157。

表9 机械组件维修模型参数估计表 Table 9 Parameters estimation of mechanical components maintenance model

i	τ _i	X_i	$\begin{matrix} \sqrt[]{\frac{n}{n + 1}} \end{matrix}$ · $\begin{matrix} \frac{X_{i} - \bar{X}}{S} \end{matrix}$	t_n-₁ $\begin{matrix} (\sqrt[]{\frac{n}{n + 1}} \cdot \frac{X_{i} - \bar{X}}{S}) \end{matrix}$	$\begin{matrix} {\hat{p}}_{i} \end{matrix}$
1	0.89	-0.1165	-1.4230	t₅ $\begin{matrix} (- 1.4230) \end{matrix}$	0.1070
2	2.00	0.6931	-0.6759	t₅ $\begin{matrix} (- 0.6759) \end{matrix}$	0.2645
3	4.11	1.4134	-0.0113	t₅ $\begin{matrix} (- 0.0113) \end{matrix}$	0.4957
4	6.62	1.8901	0.4286	t₅ $\begin{matrix} (0.4286) \end{matrix}$	0.6570
5	7.31	1.9892	0.5201	t₅ $\begin{matrix} (0.5201) \end{matrix}$	0.6874
6	14.65	2.6844	1.1616	t₅ $\begin{matrix} (1.1616) \end{matrix}$	0.8511

表9 机械组件维修模型参数估计表 Table 9 Parameters estimation of mechanical components maintenance model

同样进行d检验对模型进行拟合优度检验, 如表10所示(取显著性水平α =0.10)。

表10 三类组件维修时间模型d检验 Table 10 Maintenance time model d test of three class component

由表10可知, 所有D_n< D_n_,_α, 通过拟合优度检验。系统组件的维修时间分布函数, 如表11所示。

表11 三类系统组件维修时间分布函数 Table 11 Maintenance time distribution function of three types of system components

系统模块	$\begin{matrix} \int_{0}^{t} \end{matrix} \begin{matrix} \frac{1}{σx \sqrt[]{2 π}} \end{matrix}$ exp $\begin{matrix} \{- \frac{1}{2} {(\frac{lnx - μ}{σ})}^{2}\} \end{matrix}$ dx
机械系统	$\begin{matrix} \int_{0}^{t} \end{matrix} \begin{matrix} \frac{1}{0.9501 x \sqrt[]{2 π}} \end{matrix}$ exp $\begin{matrix} \{- \frac{1}{2} {(\frac{lnx - 1.4031}{0.9501})}^{2}\} \end{matrix}$ dx
电气系统	$\begin{matrix} \int_{0}^{t} \end{matrix} \begin{matrix} \frac{1}{0.5197 x \sqrt[]{2 π}} \end{matrix}$ exp $\begin{matrix} \{- \frac{1}{2} {(\frac{lnx - 1.3548}{0.5197})}^{2}\} \end{matrix}$ dx
辅助系统	$\begin{matrix} \int_{0}^{t} \end{matrix} \begin{matrix} \frac{1}{1.1157 x \sqrt[]{2 π}} \end{matrix}$ exp $\begin{matrix} \{- \frac{1}{2} {(\frac{lnx - 1.3349}{1.1157})}^{2}\} \end{matrix}$ dx

表11 三类系统组件维修时间分布函数 Table 11 Maintenance time distribution function of three types of system components

依据公式MTTR= $\begin{matrix} \int_{_{0}}^{^{\infty}} \end{matrix}$ tm(t)dt=exp(μ + $\begin{matrix} \frac{σ}{2} \end{matrix}$ ), 可得系统组件平均维修时间MTTR点估计值, 机械系统、电气系统和辅助系统分别为6.388、4.436和7.080 h。

2.4 数控组合机床整机平均维修时间

数控组合机床系统是3类组件组成的串联系统, 依据各系统组件故障率函数, 得到数控组合机床系统故障率函数为:

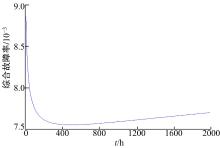
$λ (t) = \frac{1.1502}{379.0124} {(\frac{t}{379.0124})}^{0.1502} + \frac{0.9615}{352.9758} {(\frac{t}{352.9758})}^{- 0.0385} + \begin{matrix} \frac{0.7821}{450.1370} {(\frac{t}{450.1370})}^{- 0.2179} \end{matrix}$

数控组合机床系统故障率曲线如图2所示。

	Figure Option View Download New Window
	图2 数控组合机床故障率曲线Fig.2 Failure rate curve of numerical control combined machine tool

使用Matlab对系统综合率函数进行极小值编程可得, 当故障时间t=494.6 h时, 对应于数控组合机床故障率的最低, 对应的各系统组件故障率为:

λ _机 $\begin{matrix} (t) \end{matrix}$ =λ _机 $\begin{matrix} (494.6) \end{matrix}$ =0.00316

λ _电 $\begin{matrix} (t) \end{matrix}$ =λ _电 $\begin{matrix} (494.6) \end{matrix}$ =0.00289

λ _辅 $\begin{matrix} (t) \end{matrix}$ =λ _辅 $\begin{matrix} (494.6) \end{matrix}$ =0.00170

故可得故障时间t=494.6 h时, 数控组合机床整机平均维修时间为:

$\begin{matrix} MTTR (t = 494.6 h) = \frac{\sum λ_{i} MTT R_{i}}{\sum λ_{i}} = 5.812 h \end{matrix}$

因此, 最小故障率下的数控组合机床整机平均维修时间为5.812 h。

3 结束语

本文引入平均秩次法进行多重截尾故障秩次修正, 应用极大似然估计法进行系统组件故障率模型参数估计, 并进行参数修正与模型拟合性检验, 实现时间相关下系统组件故障率建模, 提高模型准确性与合理性。针对各系统组件维修时间小样本特点, 进行最小二乘法约束准则下的参数优化, 使用粒子群优化算法进行参数估计, 并进行模型拟合性检验, 建立了小样本下系统组件维修时间模型, 提高了模型精度。综合考虑数控组合机床系统组件故障时间相关性, 结合各组件维修时间模型, 建立了最小故障次数下基于组件平均维修时间加权的系统平均维修时间模型以确定系统平均维修时间, 修正传统系统维修时间设计的弊端, 为合理制定维修策略奠定基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	蔡景, 左洪福, 王华伟. 多部件系统的预防性维修优化模型研究[J]. 系统工程理论与实践, 2007, 27(2): 133-138. Cai Jing, Zuo Hong-fu, Wang Hua-wei. Research on the preventive maintenance optimization model of multi component system[J]. System Engineering Theory and Practice, 2007, 27(2): 133-138. [本文引用:1]
[2]	Dale B G, Ireland F. A study of total productive maintenance implementation[J]. Journal of Quality in Maintenance Engineering, 1995, 7(3): 183-192. [本文引用:1]
[3]	成国庆, 李玲, 唐应辉. 多态退化可修系统的最优维修更换策略[J]. 系统工程理论与实践, 20012, 32(5): 1118-1123. Cheng Guo-qing, Li Ling, Tang Ying-hui. Optimal maintenance and replacement policy for repairable system with multi state degradation[J]. System Engineering Theory and Practice, 20012, 32(5): 1118-1123. [本文引用:1]
[4]	申桂香, 谷东伟, 张英芝, 等. 数控机床最佳预防维修间隔时间的确定[J]. 重庆大学学报, 2012, 35(1): 7-10. Shen Gui-xiang, Gu Dong-wei, Zhang Ying-zhi, et al. Optimal preventive maintenance interval period of CNC[J]. Journal of Chongqing University, 2012, 35(1): 7-10. [本文引用:1]
[5]	石慧, 曾建潮. 基于寿命预测的预防性维护维修策略[J]. 计算机集成制造系统, 2014, 20(5): 1133-1140. Shi Hui, Zeng Jian-chao. Preventive maintenance strategy based on life prediction[J]. Computer Integrated Manufacturing System, 2014, 20(5): 1133-1140. [本文引用:1]
[6]	程志君, 杨征, 谭林. 基于机会策略的复杂系统视情维修决策模型[J]. 机械工程学报, 2012, 48(6): 168-174. Cheng Zhi-jun, Yang Zheng, Tan Lin. A decision model of maintenance decision model for complex systems based on opportunity strategy[J]. Journal of Mechanical Engineering, 2012, 48(6): 168-174. [本文引用:1]
[7]	蔡景, 左洪福, 刘明. 复杂系统成组维修策略优化模型研究[J]. 应用科学学报, 2006, 24(5): 533-537. Cai Jing, Zuo Hong-fu, Liu Ming. Research on the optimization model of group maintenance strategy for complex systems[J]. Journal of Applied Science, 2006, 24(5): 533-537. [本文引用:1]
[8]	李剑涛, 蒋里强, 黄立波. 装备最佳预防性维修间隔时间研究[J]. 装备指挥技术学院学报, 2004, 15(3): 26-29. Li Jian-tao, Jiang Li-qiang, Huang Li-bo. Study on the interval in the best equipment preventive maintenance[J]. Journal of the Academy of Equipment Command & Technology, 2004, 15(3): 26-29. [本文引用:2]
[9]	张英芝, 刘津彤, 申桂香, 等. 基于故障相关性分析的数控机床系统可靠性建模[J]. 吉林大学学报: 工学版, 2017, 47(1): 169-173. Zhang Ying-zhi, Liu Jin-tong, Shen Gui-xiang, et al. Reliability modeling of CNC machine tools system based on failure correlation analysis[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(1): 169-173. [本文引用:1]
[10]	申桂香, 孟书, 张英芝, 等. 平均秩次法在子系统可靠性建模中的应用[J]. 吉林大学学报: 工学版, 2014, 44(1): 101-105. Shen Gui-xiang, Meng Shu, Zhang Ying-zhi, et al. Application of average rank time method in reliability modeling for subsystems[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(1): 101-105. [本文引用:1]

2007

0.0

. 2007, 27(2):133-138 DOI:doi:10.3321/j.issn:1000-6788.2007.02.018

Research on the preventive maintenance optimization model of multi component system

多部件系统的预防性维修优化模型研究

Cai Jing , Zuo Hong-fu , Wang Hua-wei.

蔡景, 左洪福, 王华伟

针对多部件系统固定维修费用高的特点,提出采用机会维修策略,将预防性维修和故障维修有机结合起来,从而分摊系统的固定维修费用,实现节约维修费用的目的.分析了系统的故障率特性,确定了系统中各部件最小维修、故障更换、机会更换、预防性更换的概率.在此基础上,以最小化维修成本为目标建立了优化模型.最后通过算例,将优化结果与原有的维修策略的结果进行了比较,说明了模型的合理性.

... 0 引言有统计表明^[1],数控组合机床维修保养费用在整个寿命周期费用中的占比高达20%~30% ...

1995

0.0

... Dale等^[2]建立了以可靠性为约束条件维修费用最小维修计划优化模型 ...

0.0

. , 32(5):1118-1123 DOI:doi:10.3969/j.issn.1000-6788.2012.05.025

Optimal maintenance and replacement policy for repairable system with multi state degradation

多态退化可修系统的最优维修更换策略

Cheng Guo-qing , Li Ling , Tang Ying-hui.

成国庆, 李玲, 唐应辉

A maintenance model for a deteriorating series system with multi-state is proposed. Assume that every component in the system has more than one failure states. The occurrence of a failure state of any one type is mutually exclusive and stochastic. The failed components can not be repaired as good as new. Under these assumptions, an explicit expression of average cost rate of such system is given by using generalized geometric process and the replacement policy based on the failure numbers of the components. The optimal replacement policy is derived analytically. Finally, a numerical example is given to validate the replacement policy.

针对工程技术领域中的多失效状态的串联退化可修系统, 提出了一种维修更换模型. 假设系统中的部件有多个失效状态, 故障时以一定的概率进入其中某个状态, 部件不能修复如新. 以系统中部件的故障次数为更换策略, 系统的平均费用率为目标函数, 利用推广的几何过程理论建立数学模型, 证明了最优维修更换策略的存在性. 最后, 通过一个数值例子验证了本方法的有效性.

... 成国庆等^[3]针对工程技术领域中的串联可修系统,以系统中部件的故障次数为更换策略,系统平均费用率为目标函数,提出了一种维修更换模型 ...

2012

0.0

. 2012, 35(1):7-10 DOI:doi:10.11835/j.issn.1000-582x.2012.01.003

Optimal preventive maintenance interval period of CNC

数控机床最佳预防维修间隔时间的确定

Shen Gui-xiang , Gu Dong-wei , Zhang Ying-zhi

申桂香, 谷东伟, 张英芝

摘　要：以采集的5台国产某型号数控机床1a的现场故障数据为基础,通过参数估计、线性相关性检验和假设检验确定故障过程服从二参数威布尔分布;在有效性最大原则的基础上,提出一种在修复型维修状态下的最佳预防维修间隔时间模型,并求得此型号数控机床的最佳预防维修间隔时间;最后根据机床的最佳预防维修间隔时间建立相应的维修计划,最大限度保证了机床的使用性能并减少企业维修费用。

... 申桂香等^[4]在有效性最大的基础上,提出一种在修复型维修状态下的最佳预防维修间隔时间模型,最大限度保证机床的使用性能并减少维修费用 ...

2014

0.0

. 2014, 20(5):1133-1140 DOI:doi:10.13196/j.cims.2014.05.shihui.1133.8.20140516

Preventive maintenance strategy based on life prediction

基于寿命预测的预防性维护维修策略

Shi Hui , Zeng Jian-chao.

石慧, 曾建潮

Aiming at the inestimable complicate system of degradation distribution function,the optimal decision for remaining useful life prediction and preventive maintenance was proposed,and a preventive maintenance strategy was presented based on effective prediction of remaining life for complex system.Under the conditions of unknown degradation distribution function,the average remaining useful life of the known life distribution function was forecasted as the threshold to draft preventive maintenance strategies.According to the theory of renewal process,an optimization model with the system prediction interval and the threshold of preventive maintenance as the optimization variables and the minimum average maintenance cost as the target function was established.By using Particle Swarm Optimization (PSO),the optimal preventive cycle and maintenance threshold of system were obtained,and the long-run average cost rate was the lowest.The civil aeroengine operation of Weibull distribution and the transformer of electromagnet control gyrocompass in the navigation equipment of Normal distribution were taken as examples to verify the feasibility of proposed strategy.

针对退化分布函数难以估计的复杂系统,研究了剩余寿命预测及预防性维护维修最优决策问题,提出一种基于复杂系统剩余寿命有效预测的预防性维护维修策略。在系统退化状态分布函数未知的条件下,由已知的设备寿命分布函数预测其平均剩余寿命,以平均剩余寿命为阈值制定预防性维护维修策略。根据更新过程理论,建立了以系统的预测间隔、预防性维护阈值为优化变量和最小化平均维护维修费用为目标函数的优化模型。采用微粒群算法进行优化求解,得到系统最佳的预测周期和维护维修阈值,并使系统长期运行的平均费用率最低。分别以在翼寿命符合威布尔分布的民航发动机和寿命分布符合正态分布的航海设备电控罗经中的某型变压器为例,验证了所提维护维修策略的可行性。

... 石慧等^[5]提出一种基于复杂系统剩余寿命有效预测的预防性维护维修策略,其优化模型的目标函数是最小化平均维护费用 ...

2012

0.0

. 2012, 48(6):168-174

A decision model of maintenance decision model for complex systems based on opportunity strategy

基于机会策略的复杂系统视情维修决策模型

Cheng Zhi-jun , Yang Zheng , Tan Lin.

程志君, 杨征, 谭林

... 程志君等^[6]针对部件间存在经济相关性的复杂系统,提出一类基于机会策略的视情维修优化模型 ...

2006

0.0

. 2006, 24(5):533-537 DOI:doi:10.3969/j.issn.0255-8297.2006.05.018

Research on the optimization model of group maintenance strategy for complex systems

复杂系统成组维修策略优化模型研究

Cai Jing , Zuo Hong-fu , Liu Ming.

蔡景, 左洪福, 刘明

对复杂系统提出了采用成组维修策略.根据成组维修的特点,分析了复杂系统维修费用构成和系统利用率,在此基础上,以故障风险为约束,以系统总体维修费用的最小化、系统利用率最大化为目标,建立了复杂系统成组维修策略的优化模型.最后采用遗传算法,以某民用飞机的空调系统维修为例对模型的有效性进行了验证.

... 蔡景等^[7]以故障风险为约束,以系统总体维修费用最小化、系统利用率最大化为目标,建立了复杂系统成组维修策略的优化模型 ...

2004

0.0

. 2004, 15(3):26-29

Study on the interval in the best equipment preventive maintenance

装备最佳预防性维修间隔时间研究

Li Jian-tao , Jiang Li-qiang , Huang Li-bo.

李剑涛, 蒋里强, 黄立波

... 李剑涛等^[8]从装备的可靠性和维修费用出发,重点研究了年龄维修策略的维修间隔期和定期检测策略的检测时间间隔的定量分析方法 ...

... 因为多重截尾数据的存在,致使被研究组件的故障次序发生变化,为此,本文采用Johnson法^[8],引入秩增量来修正这一秩次变动 ...

2017

0.0

. 2017, 47(1):169-173 DOI:doi:10.13229/j.cnki.jdxbgxb201701025

Reliability modeling of CNC machine tools system based on failure correlation analysis

基于故障相关性分析的数控机床系统可靠性建模

Zhang Ying-zhi , Liu Jin-tong , Shen Gui-xiang

张英芝, 刘津彤, 申桂香

摘　要：基于数控机床相关故障机理分析进行组件可靠性建模,并以组件可靠性模型为边缘分布,引入Copula函数,建立联合可靠性函数,通过样本得到Kendall秩相关系数来进行Copula函数参数估计,为相关故障条件下系统可靠性分析提供一种新的技术方法。最后,以加工中心为例,将本文方法与采用传统方法的组件可靠性串联模型、不考虑故障相关方向性的Copula函数模型进行对比,结果证明了模型的合理性和有效性。

... 因此,本文将考虑系统组件的故障时间相关性,建立基于故障时间相关的组件故障率模型^[9],结合各组件维修时间模型,建立基于组件平均维修时间加权的系统平均维修时间模型以确定最小故障次数下系统平均维修时间 ...

2014

0.0

. 2014, 44(1):101-105 DOI:doi:10.13229/j.cnki.jdxbgxb201401018

Application of average rank time method in reliability modeling for subsystems

平均秩次法在子系统可靠性建模中的应用

Shen Gui-xiang , Meng Shu , Zhang Ying-zhi

申桂香, 孟书, 张英芝

This paper presents a method of the reliability modeling of a series system. Such a system is composed of several mutual independent subsystems, and the system life-time obeys two-parameter Weibull distribution. In this method, when one of subsystems is failure, the fault data of the other subsystems are processed as censored data, and the failure sequence is revised using the average rank time method. This method can be applied for model parameter estimation and fitting test to reduce the modeling error and improve the accuracy. Finally, as a case study, the real data of a Computerized Numerical Control (CNC) are used to demonstrate the application of the proposed method, which verifies the effectiveness and applicability of the method.

讨论了由几个相互独立的子系统组成的串联系统的寿命服从两参数威布尔分布时，其子系统的可靠性建模问题。并指出当某子系统出现故障时，其他子系统故障数据按照截尾数据处理，然后用平均秩次法对故障顺序修正，据此进行模型参数估计和拟合性检验，可以达到减小建模误差、提高拟合精度的目的。最后以某加工中心现场试验数据为例介绍该方法的具体应用过程，以验证该方法的有效性和实用性。

... 1 基于时间相关的系统组件可靠性建模综合考虑系统其余组件故障时间和定时截尾可靠性试验等多重截尾数据对系统组件故障时间的影响,引入平均秩次法对故障时间次序进行修正,应用近似中位秩法建立经验分布函数,采用极大似然估计法(MLE)法进行参数估计,采用d检验法进行模型拟合性检验,以确定各系统组件可靠性函数^[10] ...