神经元是神经系统结构和功能的基本单位, 是神经系统的关键组成部分, 具有感受刺激和传导兴奋的功能^[1]。同步是神经元的基本行为, 在神经系统中是广泛存在的。随着非线性动力学理论和方法的发展, 同步也从之前的周期振子扩大到混沌系统的同步, 在研究混沌同步的过程中, 专家学者们基于实际背景提出了很多实现混沌同步的有效方法, 比如自适应同步^[2]、反馈同步^[3]、噪声同步^[4]和脉冲同步^[5], 这些实现同步的方法已经在理论上和实践中得到了验证, 并且在神经性疾病^[6]以及通信保密系统^[7]的应用中体现了重要的价值。

噪声广泛存在于自然界的各个领域, 传统的观念认为噪声会影响神经元信息传递的准确性, 而实际上噪声可以促使神经元产生丰富的放电模式。如:Postnov等^[8]研究了噪声对耦合的可兴奋性Morris-Lecar神经元的影响, 将噪声强度作为神经元控制系统频率差异的参数, 给出了外界噪声诱导耦合同步和随机自共振现象之间的联系。Casado^[9]研究了内噪声作用下两个电耦合Hodgkin-Huxley神经元相位同步问题, 研究发现, 无噪声的状态下神经元处于静息状态, 内噪声的状态下两个神经元处于同步放电状态, 而且使两个神经元的相对相位差达到不同的数值范围, 包括反相与同相相位锁定。Pablo等^[10]研究了外界噪声参与下的化学突触耦合Morris-Lecar神经元模型的相关动力行为, 研究发现, 与电突触耦合相比较, 化学突触耦合在优化噪声强度增加的相关性行为更加有效, 并详细说明了造成这种不同的原因。Wu等^[11]研究了噪声诱导的两个未耦合的非全同Hindmarsh-Rose神经元的同步, 说明通过噪声和改变其中一个神经元的参数可以使两个神经元达到广义同步。李娜等^[12]以电耦合的Terman-Wang小世界神经元网络系统作为研究对象, 研究了空间关联噪声影响下神经元网络系统的同步动力学, 研究发现, 较大的空间噪声关联系数、耦合强度以及节点平均度均能够对神经元网络系统同步放电现象起到积极作用。

本文建立了具有两个化学突触耦合的Hindmarsh-Rose数学模型, 研究了化学突触耦合神经元系统的基本现象, 观察系统的发、放电活动以及系统同步的变化情况, 并分析了高斯白噪声对化学突触耦合同步的影响。

Hindmarsh-Rose神经元模型是通过电压钳的实验得到的蜗牛神经元细胞的数据表达式, 该神经元模型不考虑神经元细胞膜上单个离子通道形成的作用, 而把神经元细胞看成一个整体, 它是一个三维的动力学数学模型。Hindmarsh-Rose神经元可以很好地解释神经元的放电规律和非周期模型等一些动力学特性, 而且该模型简单, 研究起来相对容易, 因此被许多专家学者用作研究神经元放电的理想化模型^[13]。本文采用的模型是Krasimira Tsaneva-Atanasov构造的Hindmarsh-Rose模型的神经元模型^[14], 简称HR模型, 其表达式如下:

dxdt=-s-ax3+x2-y-bzdydt=φx2-ydzdt=εsa1x1+b1-kz（1）

式中:x为神经元的膜电压; y为与神经元细胞内电流相关的恢复变量; z为慢变适应性的电流; a、b、a₁、b₁、k、s为系统的参数; φ 和ε 为控制时间尺度的参数, 对应取值为:φ =1, a=0.5, b=1, a₁=-0.1, k=0.2, 这些参数的详细说明参见文献[14]。

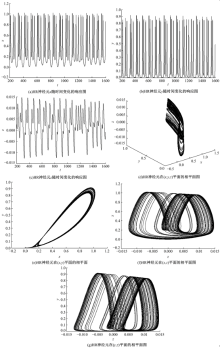
当b₁=-0.045, ε =0.02, s=-1.61时, 神经元处于混沌放电模式, 其时间响应图和相平面图如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 HR神经元在参数b1=-0.045, ε =0.02, s=-1.61时的时间响应图和相平面图Fig.1 Time response diagram and phase plane diagram of HR neurons with b1=-0.045, ε =0.02, s=-1.61

为了验证HR神经元系统的同步行为, 本文建立了化学突触耦合的两个HR神经元系统的数学模型, 其动力学方程描述为:

dx1dt=-s-ax13+x12)-y1-bz1+ D(Vsyn-x1)/{1+exp[-σ(x2-θ)]}dy1dt=φ(x12-y1)dz1dt=ε(sa1x1+b1-kz1)dx2dt=-s-ax23+x22)-y2-bz2+ D(Vsyn-x2)/{1+exp[-σ(x1-θ)]}dy2dt=φ(x22-y2)dz2dt=ε(sa1x2+b1-kz2)(2)

式中:V_syn为神经元突触的可逆电位, V_syn=2; θ 为突触阈值, θ =-0.35; σ 为兴奋或抑制开始的比率常数, σ =10; D为耦合强度。

分别取D=0和D=0.4进行数值仿真, 为了更好地研究耦合研究神经元同步情况, 本文引入耦合神经元的同步差e₀=x₂-x₁、e₁=y₂-y₁、e₂=z₂-z₁、e₃= 13( e0+ e1+ e2)来分析神经元耦合同步变化情况。

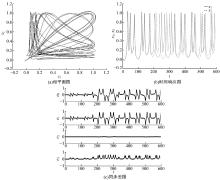
首先, 本文考虑在无耦合强度的情况下(即耦合强度D=0时)两个HR神经元模型的放电活动。在耦合强度D=0时, 求解方程可以得到化学突触耦合的两个HR神经元在(x₁, x₂)平面上的相平面图, 如图2(a)所示, 从图中可以看出, 相平面呈现出无规则不相关的运动, 说明系统此时处于非同步状态。从图2(b)x₁和x₂随时间变化的时间响应图可以看出, 系统的时间响应图呈现出无规则的混沌放电活动, 且同一时刻的x₁和x₂取值不同, 说明系统处于混沌状态。从图2(c)耦合神经元系统之间随着时间变化的同步差可以发现, 随着时间的变化, 同步差一直存在, 这也说明了两个神经元系统并没有处于同步状态。通过以上分析可以得出, 在耦合强度D=0时, 两个神经元系统处于混沌放电状态, 且处于非同步状态。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 D=0时两HR化学突触耦合神经系统Fig.2 Two HR chemical synapses coupling neural system when D=0

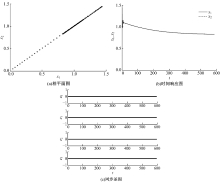
然后, 本文分析耦合强度D=0.4时两个HR神经元化学突触耦合同步的情况。同样取耦合强度D=0.4时两个HR神经元系统在(x₁, x₂)平面上的相平面图, 如图3(a)所示, 从图中可以看出, 相平面呈现斜率为1的直线, 尽管图中有零星的孤立点存在, 但这些点同样处于斜率为1的直线上, 说明x₁和x₂的取值相同, 此时系统处于同步状态。从图3(b)x₁和x₂随时间变化的时间响应图可以看出, 图像呈现出曲线运动, 且x₁和x₂的取值曲线重叠, 说明x₁和x₂的取值相同。为了更好地观察两神经元的同步情况, 同样引入同步差图, 如图3(c)所示, 从图中可以清晰地发现, 随着时间的变化, 同步差的极大值一直为0, 说明此时两神经元耦合系统处于同步状态。通过以上分析可以得出, 在耦合强度D=0.4时, 系统处于同步状态。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 D=0.4时的两HR化学突触耦合神经系统Fig.3 Two HR chemical synapses coupling neural system when D=0.4

通过以上分析可以发现, 神经元的耦合强度能够影响耦合神经元系统的放电活动以及耦合神经元系统的同步状态。通过适当调整耦合强度, 可以使两个神经元系统从非同步的系统变为同步的系统, 这对研究神经元之间的耦合同步以及展示神经元的丰富的放电活动是很有必要的, 同时能够进一步促进神经生理实验的发展。

在神经系统中, 离子通道的打开和关闭、神经递质的释放等都有可能会产生噪声, 因此, 噪声广泛存在于神经系统中。根据噪声的起源以及其他相关性质, 噪声可以划分为很多不同的类型:根据噪声的起源不同噪声可以分为外噪声和内噪声。根据噪声的统计分布不同, 噪声又可分为泊松噪声、高斯噪声等。根据噪声的自关联时间的不同, 噪声又可以分为白噪声和色噪声等^[15]。

大量相互独立的抑制性和兴奋性突触电流噪声通常近似高斯分布, 因此本文主要研究高斯白噪声对神经元耦合系统同步的影响, 高斯白噪声的统计分布服从高斯分布, 而功率谱密度又是均匀分布的噪声。如果用ξ (t)表示噪声, 其统计性质满足:

ξ(t1)ξ(t2)⋯ξ(t2n-1)=ξ(t1)ξ(t2)⋯ξ(t2n)=(C)n∑δ(ti1-ti2)δ(ti3-ti4)⋯δ(ti(2n-1)-ti2n)(3)

而且, 当ν ≠ μ 时, i_ν ≠ i_μ 。仅取前两阶矩, 有

< ξ(t)> =0< ξ(t)ξ(t')> =2Cδ(t-t'(4)

式中:C为噪声强度; δ (· )为Dirac函数。

本文引入两个HR化学突触耦合神经元系统, 使其加入相同的高斯白噪声, 方程表达式如下:

dx1dt=-s-ax13+x12)-y1-bz1+ D(Vsyn-x1)/{1+exp[-σ(x2-θ)]}+ξ(t)dy1dt=φ(x12-y1)dz1dt=ε(sa1x1+b1-kz1)dx2dt=-s-ax23+x22)-y2-bz2+ D(Vsyn-x2)/{1+exp[-σ(x1-θ)]}+ξ(t)dy2dt=φ(x22-y2)dz2dt=ε(sa1x2+b1-kz2)(5)

首先, 本文考虑Gauss白噪声不存在的情况, 即令耦合强度D=0.032, 噪声不存在, 仿真得到HR神经元电突触耦合系统在(x₁, x₂)平面上的相平面图, 如图4(a)所示, 以及x₁和x₂随时间变化的时间响应图, 如图4(b)所示。从图中可以看到, x₁和x₂都呈现出不规则运动, 说明此时两个HR神经元系统处于混沌放电活动, 从图中还可发现, 在同一时刻, x₁和x₂的取值并不相同, 说明两神经元并没有达到同步状态。为了更好地观察两神经元是否处于同步状态, 同样引入耦合神经元同步差图, 如图4(c)所示。从图中可以清晰地观察到, 随着时间的变化, 同步差一直存在, 且两神经元的差值也一直在变化, 说明系统处于非同步状态。通过以上分析可以得出, 在耦合强度D=0.032, 噪声不存在情况下, 两个神经元化学突触耦合处于混沌运动, 并且处于非同步状态。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 D=0.032, 噪声ξ (t)不存在时的两耦合HR神经元系统Fig.4 Two coupled HR neuron system when noise ξ (t) is not in existence and D=0.032

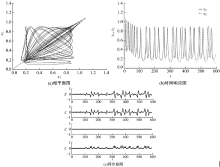
接着, 本文考虑噪声存在时对HR神经元化学突触耦合系统的同步及放电活动的影响。同样, 取耦合强度D=0.032, 引入高斯白噪声, 通过仿真得到HR神经元化学突触耦合系统在(x₁, x₂)平面上的相平面图, 如图5(a)所示。从图中可以看到, 相平面呈现出斜率为1的直线, 虽然图中有零星的孤立点存在, 但这些点同样处于斜率为1的直线上, 说明x₁和x₂的取值相同, 此时系统处于同步状态。然后, 本文得到了x₁和x₂随时间变化的时间响应图, 如图5(b)所示, 图像呈现曲线运动, 且x₁和x₂的取值曲线重叠, 说明x₁和x₂的取值相同。同样, 在图5(c)同步差图中也可以清晰地观察到, 随着时间的变化, 同步差一直为零, 说明两神经元耦合系统达到同步状态。通过以上分析可以得出, 在耦合强度D=0.032, 高斯白噪声存在时, 系统处于同步状态。

图5

Fig.5

	Figure Option ViewDownloadNew Window
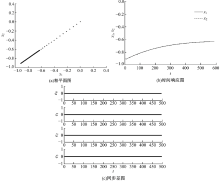	图5 D=0.032, 噪声ξ (t)存在时的两耦合HR神经元系统Fig.5 Two coupled HR neuron system when noise ξ (t) exists and D=0.032

经过以上分析可以得到, 两化学突触耦合神经元系统在不同步的情况下, 通过在两化学突触耦合神经元系统中分别添加相同的高斯白噪声, 可以使系统变为同步状态, 这也说明了噪声可以诱发化学突触耦合神经元的同步。

(1)非耦合情况下, 两个处于混沌放电的神经元不能达到同步, 当耦合强度达到一定程度时, 如D=0.4时, 系统可以达到耦合同步。

(2)耦合和噪声共同作用可以使系统更快地达到同步, 如D=0.032, 噪声不存在的情况下, 系统不能达到同步状态; 当噪声ξ (t)存在时, 系统很快达到同步。