具有测量时滞的不确定系统的递推鲁棒滤波

引用本文

冯建鑫. 具有测量时滞的不确定系统的递推鲁棒滤波. 吉林大学学报（工学版）, 2017, 47(5): 1561-1567
FENG Jian-xin. Recursive robust filtering for uncertain systems with delayed measurements. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1561-1567 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705031
Permissions

具有测量时滞的不确定系统的递推鲁棒滤波

冯建鑫

南京航空航天大学航天学院,南京 210016

作者简介:冯建鑫(1982-),男,副研究员,博士.研究方向:鲁棒滤波与数据融合,伺服控制.E-mail:fengjx774@163.com

基金项目:国家自然科学基金项目(61203030); 中央高校基本科研业务费专项基金项目(NS2017064); 南京航空航天大学引进人才科研启动基金项目(90YAH16033)

摘要

针对模型参数随机不确定性和测量时滞现象,提出了一种基于垂直投影定理和新息分析的递推鲁棒滤波方法。该方法首先将原系统转化成一个含有跨时相关性噪声的随机不确定性系统,接着重新计算了新息,然后用数学归纳法证明所得到的新息是一个互不相关的序列,最后用新息分析和垂直投影定理获得了所期望的递推鲁棒滤波器。该滤波器设计方法不需要将跨时相关性噪声进行状态增广,因而计算量小、精度高。仿真实验验证了该方法的有效性。

关键词: 自动控制技术; 数学归纳法; 垂直投影定理; 测量时滞; 随机不确定性; 跨时相关性噪声

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2017)05-1561-07

Recursive robust filtering for uncertain systems with delayed measurements

FENG Jian-xin

College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Abstract

A recursive robust filtering method based on the orthogonal projection and an innovation analysis approach is proposed for stochastic uncertain systems with delayed measurements. First, the original system is transformed into a stochastic uncertain system with correlated measurement noises, and the innovations are recalculated. Then, by applying the mathematical induction, the newly obtained innovations are proofed to be uncorrelated with each other. Finally, the desired recursive robust filter is designed via an innovation analysis approach and the orthogonal projection theorem. Without resorting to state augmentation, the proposed filter treats the noise correlated across time directly. Therefore, the desired filter has less computational burden, but a high computational accuracy. Simulation results demonstrate the effectiveness of the proposed approach.

Key words: automatic control technology; mathematical induction; orthogonal projection theorem; delayed measurement; stochastic uncertainty; noises correlated across time

Show Figures

0 引言

卡尔曼滤波理论自诞生之初便广泛应用于航空航天和信号处理等军事及民用领域^{[1, 2]}。它建立在精确数学模型之上, 并要求传感器测量信息实时可得。然而, 在实际中, 目标系统和系统模型之间的参数误差不可避免, 这也是模型参数不确定性始终是控制和滤波问题的一个研究热点的重要原因。模型参数不确定性的种类很多, 乘性噪声作为模型随机不确定性的重要一类广泛存在于航空航天、无线电通信传输等领域^{[3, 4]}。由于依赖于目标系统状态, 乘性噪声的二阶统计特性往往无法获得, 这也为相应滤波器和控制器的设计带来困难。目前为止, 国内外学者在含乘性噪声的随机动态滤波器和控制器设计上做了不少工作形成了包括基于game理论和线性矩阵不等式等的研究方法^{[5, 6]}。

随着网络技术的发展, 网络广泛应用于控制和滤波领域^{[7, 8, 9]}。在网络系统当中, 传感器测量得到的数据通过网络进行传输, 由于带宽等一系列原因, 数据在传输过程中将不可避免产生时滞。Liu等^[10]将本质为随机时变的网络时滞现象描述为确定性时滞。针对这种情况, Yaz等^[11]应用一个已知概率的伯努利分布序列来描述这类网络时滞现象, 并在此模型基础上, Yaz设计了一个线性无偏滤波器。然而文献[11]得到无偏滤波器是次优的, 因为状态向量增广中产生的跨时相关性有色噪声仍被当成互不相关的白噪声来处理。Wen等^[12]利用将跨时相关性噪声进行状态增广的方法得到了一个最优线性滤波器, 然而系统维数的增大必将带来沉重的计算负担, 并且将噪声当成状态进行估计本身就是件困难的事情, 很难进一步提高系统估计精度^{[8, 9, 13]}, 另外Wen等得到的滤波器非递推, 计算时需占用较大内存。

鉴于以上分析, 本文在前人工作基础上进一步研究了测量时滞随机不确定性系统的递推鲁棒滤波器设计。新获得的递推鲁棒滤波器依赖于数学归纳法, 新息分析和垂直投影定理; 对跨时相关性噪声采用直接处理逐步分析的方式。最后, 仿真实验验证了本方法的有效性和优越性。

1 问题阐述

考虑下面含有传感器测量信息时滞和乘性噪声的随机参数动态系统:

${\overset{⌒}{x}}_{k + 1} = ({\overset{⌒}{A}}_{k} + {\overset{⌒}{A}}_{s, k} η_{k}) {\overset{⌒}{x}}_{k} + {\overset{⌒}{B}}_{k} ω_{k}$ (1)

${\overset{⌒}{y}}_{k} = {\overset{⌒}{C}}_{k} {\overset{⌒}{x}}_{k} + {\overset{⌒}{v}}_{k}$ (2)

$y_{k} = (1 - λ_{k}) {\overset{⌒}{y}}_{k} + λ_{k} {\overset{⌒}{y}}_{k - 1}$ （3）

式中: $\begin{matrix} {\overset{⌒}{x}}_{k} \end{matrix}$ ∈ ℝⁿ是要估计的系统状态; 初始状态 $\begin{matrix} {\overset{⌒}{x}}_{0} \end{matrix}$ 具有均值 $\begin{matrix} {\bar{\overset{⌒}{x}}}_{0} \end{matrix}$ 和方差 $\begin{matrix} {\overset{⌒}{P}}_{0} \end{matrix}$ , 并且初始状态与其他噪声信号均不相关。 $\begin{matrix} {\overset{⌒}{y}}_{k} \end{matrix}$ ∈ ℝ^m是传感器的测量输出, 测量时刻k=0时, 初值 $\begin{matrix} {\overset{⌒}{y}}_{- 1} \end{matrix}$ 取为0, y_k∈ ℝ^m是滤波器实际计算时用到的测量信息; $\begin{matrix} {\overset{⌒}{A}}_{k} \end{matrix}$ 、 $\begin{matrix} {\overset{⌒}{A}}_{s, k} \end{matrix}$ 、 $\begin{matrix} {\overset{⌒}{B}}_{k} \end{matrix}$ 和 $\begin{matrix} {\overset{⌒}{C}}_{k} \end{matrix}$ 是具有合适维数的矩阵; η _k∈ ℝ, ω _k∈ ℝ^nl和 $\begin{matrix} {\overset{⌒}{v}}_{k} \end{matrix}$ ∈ ℝ^m是互不相关的零均值白噪声, 其协方差分别为I₁, Q_k> 0和 $\begin{matrix} {\overset{⌒}{R}}_{k} \end{matrix}$ > 0; λ _k∈ ℝ是一个具有如下统计特性并且与系统噪声和初始状态均不相关的伯努利序列:

$\begin{matrix} \{\begin{matrix} Prob \{λ_{k} = 1\} = E \{λ_{k}\} = β_{k} \\ Prob \{λ_{k} = 0\} = 1 - E \{λ_{k}\} = 1 - β_{k} \\ σ_{k}^{2} = E \{(λ_{k} - β_{k})^{2}\} = (1 - β_{k}) β_{k} \end{matrix} \end{matrix}$ （4）

式中:β _k∈ $\begin{matrix} [\begin{matrix} 0 & 1 \end{matrix}] \end{matrix}$ 是一个已知的标量; Prob{· }表示事件{· }发生的概率; E{· }表示数学期望。

注释1:时滞模型(2)(3)在文献[11]、[12]和[13]等中得到了广泛的应用。该模型的优势在于意义明确、结构简单, 而且上一步的测量包含了最接近本次测量的有用信息, 滞后性相对较小。

通过定义

$\begin{matrix} \{\begin{matrix} x_{k} = [\begin{matrix} {\overset{⌒}{x}}_{k} \\ {\overset{⌒}{x}}_{k - 1} \end{matrix}], v_{k} = [\begin{matrix} {\overset{⌒}{v}}_{k} \\ {\overset{⌒}{v}}_{k - 1} \end{matrix}], B_{k} = [\begin{matrix} {\overset{⌒}{B}}_{k} \\ 0 \end{matrix}] \\ A_{k} = [\begin{matrix} {\overset{⌒}{A}}_{k} & 0 \\ I_{n} & 0 \end{matrix}], A_{s, k} = [\begin{matrix} {\overset{⌒}{A}}_{s, k} & 0 \\ 0 & 0 \end{matrix}] \\ C_{k} = [\begin{matrix} (1 - λ_{k}) {\overset{⌒}{C}}_{k} & λ_{k} {\overset{⌒}{C}}_{k - 1} \end{matrix}] \\ D_{k} = [\begin{matrix} (1 - λ_{k}) I_{m} & λ_{k} I_{m} \end{matrix}] \end{matrix} \end{matrix}$ （5）

系统(1)~(3)可以表示成如下紧凑形式:

$\begin{matrix} \begin{matrix} x_{k + 1} = (A_{k} + A_{s, k} η_{k}) x_{k} + B_{k} ω_{k} (6) \\ y_{k} = C_{k} x_{k} + D_{k} v_{k} (7) \end{matrix} \end{matrix}$

式中:v_k为辅助系统(6)(7)的测量噪声, 由式(5)可知, v_k均值为0, 并具有如下的统计特性:

$\begin{matrix} E \{v_{k} {v^{T}}_{t}\} = R_{k} δ_{k - t} + R_{k, k - 1} δ_{k - t - 1} + R_{k, k + 1} δ_{k - t + 1} (8) \end{matrix}$

式中:矩阵R_k、R_k_,_k-₁和R_k_,_k+₁满足下式:

$\begin{matrix} \{\begin{matrix} R_{k} = [\begin{matrix} {\overset{⌒}{R}}_{k} & 0 \\ 0 & {\overset{⌒}{R}}_{k - 1} \end{matrix}], R_{k, k + 1} = [\begin{matrix} 0 & {\overset{⌒}{R}}_{k} \\ 0 & 0 \end{matrix}] \\ R_{k, k - 1} = [\begin{matrix} 0 & 0 \\ {\overset{⌒}{R}}_{k - 1} & 0 \end{matrix}] \end{matrix} \end{matrix}$ （9）

由式(8)能够看到, 测量噪声v_k不再是零均值的白噪声, 而是一个跨时自相关的有色噪声。具体来说就是, k时刻的测量噪声与k+1和k-1时刻的测量噪声相关, 其协方差矩阵分别为R_k_,_k-₁和R_k_,_k+₁。

对于跨时相关性噪声, 传统的处理方法是进行状态向量的增广, 将跨时相关性噪声作为状态的一个分量来进行估计。然而, 系统维数的进一步增大, 必然带来计算量的增加; 另外将噪声作为状态的一个分量进行估计也很难得到较高的精度, 噪声的估计误差势必将降低整个系统状态的估计精度。因此, 本文在接下来对于辅助系统(6)(7)的滤波器设计中没有采用状态向量增广的方法, 而是采用了基于垂直投影定理的新息分析的方法。这种方法的优点是新息构成一个互不相关的序列, 物理意义明确, 便于分析和设计计算。

2 递推鲁棒滤波器设计

在进行递推鲁棒滤波器设计之前, 首先引入下面的引理, 这对简化滤波器设计非常有用。

引理1 对于辅助系统(6)(7)中出现的随机参数矩阵C_k和D_k, 有如下结论:

$\begin{matrix} \{\begin{matrix} {\bar{C}}_{k} = E \{C_{k}\} = [\begin{matrix} (1 - β_{k}) {\overset{⌒}{C}}_{k} & β_{k} {\overset{⌒}{C}}_{k - 1} \end{matrix}] \\ {\bar{D}}_{k} = E \{D_{k}\} = [\begin{matrix} (1 - β_{k}) I_{m} & β_{k} I_{m} \end{matrix}] \\ C_{e, k} = [\begin{matrix} - {\overset{⌒}{C}}_{k} & {\overset{⌒}{C}}_{k - 1} \end{matrix}], D_{e} = [\begin{matrix} - I_{m} & I_{m} \end{matrix}] \\ J_{k} = (λ_{k} - β_{k}), {\tilde{C}}_{k} = C_{k} - {\bar{C}}_{k} = J_{k} C_{e, k} \\ {\tilde{D}}_{k} = D_{k} - {\bar{D}}_{k} = J_{k} D_{e} \end{matrix} \end{matrix}$ （10）

式中:矩阵 $\begin{matrix} {\bar{C}}_{k} \end{matrix}$ 和 $\begin{matrix} {\bar{D}}_{k} \end{matrix}$ 是随机参数矩阵C_k和D_k的数学期望; 矩阵C_e_,_k、D_e、J_k、 $\begin{matrix} {\tilde{C}}_{k} \end{matrix}$ 和 $\begin{matrix} {\tilde{D}}_{k} \end{matrix}$ , 是为了计算简洁而定义的中间矩阵。

证明:式(10)可由式(4)和式(5)得到。证毕

引理2 状态乘积的期望矩阵X_k=E{x_k $\begin{matrix} {x^{T}}_{k} \end{matrix}$ }满足如下的递推形式:

$\begin{matrix} \{\begin{matrix} X_{k + 1} = A_{k} X_{k} {A^{T}}_{k} + A_{s, k} X_{k} {A^{T}}_{s, k} + B_{k} Q_{k} {B^{T}}_{k} \\ X_{0} = diag ({\bar{\overset{⌒}{x}}}_{0} {\bar{\overset{⌒}{x}}}^{T}_{0}, 0) + diag ({\overset{⌒}{P}}_{0}, 0) \end{matrix} \end{matrix}$ （11）

式中:diag(· )表示对角线矩阵, $\begin{matrix} {\overset{⌒}{x}}_{- 1} \end{matrix}$ 取为0。

证明:引理2可由式(5)(6), 系统状态的初始条件以及随机不确定性与过程噪声互不相关的特性直接得到。证毕

在传统的卡尔曼滤波理论中, 新息ε _k有如下的计算形式:

$\begin{matrix} ε_{k} = y_{k} - C_{k} {\hat{x}}_{k | k - 1} \end{matrix}$ （12）

式中:向量 $\begin{matrix} {\hat{x}}_{k | k - 1} \end{matrix}$ 为状态的一步预测。然而, 由于随机产生的测量时滞, 问题就变得复杂了。通过式(5)和(8)可以看到, 在本文中, 采用式(12)计算的新息是一个相关性序列, 因此需要采取措施来得到不相关的新息。

根据垂直投影定理, 用来进行滤波计算的测量向量一步预测有如下计算形式:

$\begin{matrix} {\hat{y}}_{k | k - 1} = \overset{k - 1}{\sum_{i = 1}} E \{y_{k} {ε^{T}}_{i}\} Π_{i}^{- 1} ε_{i}, k > 1 \end{matrix}$ （13）

式中: $\begin{matrix} {\hat{y}}_{k | k - 1} \end{matrix}$ 是测量向量的一步预测, Π _i是新息的均方值。由Π _i的定义可知Π _i≥ 0, Π _i=0当且仅当ε _i=0。现实中, 测量信息总有误差, 因此在计算中可以保证ε _i≠ 0, 进而Π _i可逆。考虑到测量噪声v_k一步跨时自相关, 由式(7)(8)和引理1, 期望E{y_k $\begin{matrix} {ε^{T}}_{i} \end{matrix}$ }可计算如下:

$\begin{matrix} \{\begin{matrix} E \{y_{k} {ε^{T}}_{i}\} = {\bar{C}}_{k} E \{x_{k} {ε^{T}}_{i}\}, i \leq k - 2 \\ E \{y_{k} {ε^{T}}_{k - 1}\} = {\bar{C}}_{k} E \{x_{k} {ε^{T}}_{k - 1}\} + {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} \end{matrix} \end{matrix}$ （14）

将式(14)代入到式(13), 有:

$\begin{matrix} \begin{matrix} {\hat{y}}_{k | k - 1} = \overset{k - 1}{\sum_{i = 1}} E \{y_{k} {ε^{T}}_{i}\} Π_{i}^{- 1} ε_{i} \\ = {\bar{C}}_{k} {\hat{x}}_{k | k - 1} + {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} ε_{k - 1} \end{matrix} \end{matrix}$ （15）

进而, 新息ε _k可计算如下:

$\begin{matrix} ε_{k} = y_{k} - {\bar{C}}_{k} {\overset{^{}}{x}}_{k | k - 1} - {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} ε_{k - 1}, k > 1 (16) \end{matrix}$

新息的初始值取为ε ₁=y₁。

引理3 测量噪声v_k与新息ε _j, 1≤ j≤ k-2互不相关, 即下式成立:

$\begin{matrix} E \{ε_{j} {v^{T}}_{k}\} = 0, 1 \leq j \leq k - 2 (17) \end{matrix}$

证明:用数学归纳法证明, 当j=1时有:

$\begin{matrix} \begin{matrix} E \{ε_{1} {v^{T}}_{k}\} = E \{(C_{1} x_{1} + D_{1} v_{1}) {v^{T}}_{k}\} = \\ {\bar{C}}_{1} E \{x_{1} {v^{T}}_{k}\} + {\bar{D}}_{1} E \{v_{1} {v^{T}}_{k}\} \end{matrix} \end{matrix}$ （18）

由于j≤ k-2, 有k≥ 3。测量噪声一步跨时自相关并与系统状态不相关, 因此期望E $\begin{matrix} \{x_{1} {v^{T}}_{k}\} \end{matrix}$ 和E $\begin{matrix} \{v_{1} {v^{T}}_{k}\} \end{matrix}$ 都为0, 进而j=1时引理3成立。当1≤ j≤ k-3时, 假设引理3成立, 则当1≤ j≤ k-2时, 有:

$\begin{matrix} \begin{matrix} E \{ε_{k - 2} {v^{T}}_{k}\} = E \{(y_{k - 2} - {\bar{C}}_{k - 2} {\hat{x}}_{k - 2 | k - 3} - {\bar{D}}_{k - 2} \times \\ R_{k - 2, k - 3} {\bar{D}}^{T}_{k - 3} Π_{k - 3}^{- 1} ε_{k - 3} {v^{T}}_{k} = \\ {\bar{C}}_{k - 2} E \{x_{k - 2} {v^{T}}_{k}\} + {\bar{D}}_{k - 2} E \{v_{k - 2} {v^{T}}_{k}\} \times \\ {\bar{C}}_{k - 2} \overset{k - 3}{\sum_{i = 1}} E \{x_{k - 2} {ε^{T}}_{i}\} Π_{i}^{- 1} E \{ε_{i} {v^{T}}_{k}\} - \\ {\bar{D}}_{k - 2} R_{k - 2, k - 3} {\bar{D}}^{T}_{k - 3} Π_{k - 3}^{- 1} E \{ε_{k - 3} {v^{T}}_{k}\} \end{matrix} \end{matrix}$ （19）

由于i≤ k-3, 根据假设, 期望E{ε _i $\begin{matrix} {v^{T}}_{k} \end{matrix}$ }为0。考虑到测量噪声一步跨时自相关并与系统状态不相关, 因此期望E{x_k-₂ $\begin{matrix} {v^{T}}_{k} \end{matrix}$ }和E{v_k-₂ $\begin{matrix} {v^{T}}_{k} \end{matrix}$ }都为0, 进而期望E{ε _k-₂ $\begin{matrix} {v^{T}}_{k} \end{matrix}$ }为0。证毕

引理4 式(16)得到的新息是一个互不相关的序列, 即下式成立:

$\begin{matrix} E \{ε_{l} {ε^{T}}_{j}\} = 0, l \neq j, \{\begin{matrix} l = 1, 2, \dots, k \\ j = 1, 2, \dots, k \end{matrix} \end{matrix}$ （20）

证明:不妨假设l> j, 则p=l-j≥ 1。下面将用数学归纳法来证明引理4。当k=2时, 有l=2, j=1。因此, 式(20)可计算如下:

$\begin{matrix} \begin{matrix} E \{ε_{2} {ε^{T}}_{1}\} = E \{(y_{2} - {\bar{C}}_{2} {\hat{x}}_{2 | 1} - {\bar{D}}_{2} R_{2, 1} {\bar{D}}^{T}_{1} Π_{1}^{- 1} ε_{1}) {ε^{T}}_{1}\} = \\ {\bar{C}}_{2} E \{x_{2} {ε^{T}}_{1}\} + {\bar{D}}_{2} E \{v_{2} {ε^{T}}_{1}\} - {\bar{D}}_{2} R_{2, 1} {\bar{D}}^{T}_{1} - \\ {\bar{C}}_{2} E \{E \{x_{2} {ε^{T}}_{1}\} Π_{1}^{- 1} ε_{1} {ε^{T}}_{1}\} = \\ {\bar{D}}_{2} E \{v_{2} {x^{T}}_{1}\} {\bar{C}}^{T}_{1} + {\bar{D}}_{2} E \{v_{2} {v^{T}}_{1}\} {\bar{D}}^{T}_{1} - \\ {\bar{D}}_{2} R_{2, 1} {\bar{D}}^{T}_{1} = 0 \end{matrix} \end{matrix}$ （21）

在k=q-1时, 假设式(20)成立。要想来证明引理4是成立的, 只需证明引理4在k=q时成立。这里分p=1和p> 1两种情况来进行证明。当p=1时, 有:

$\begin{matrix} \begin{matrix} E \{ε_{l} {ε^{T}}_{j}\} = E \{(y_{j + 1} - {\bar{C}}_{j + 1} {\hat{x}}_{j + 1 | j} - {\bar{D}}_{j + 1} R_{j + 1, j} \times \\ {ε^{T}}_{j} Π_{j}^{- 1} ε_{j} {ε^{T}}_{j} = \\ E \{y_{j + 1} {ε^{T}}_{j}\} - {\bar{C}}_{j + 1} E \{{\hat{x}}_{j + 1 | j} {ε^{T}}_{j}\} - \\ {\bar{D}}_{j + 1} R_{j + 1, j} {\bar{D}}^{T}_{j} Π_{j}^{- 1} E \{ε_{j} {ε^{T}}_{j}\} = \\ {\bar{D}}_{j + 1} E \{v_{j + 1} {ε^{T}}_{j}\} - {\bar{D}}_{j + 1} R_{j + 1, j} {\bar{D}}^{T}_{j} \times \\ {\bar{C}}_{j + 1} \overset{j - 1}{\sum_{i = 1}} E \{x_{j + 1} {ε^{T}}_{i}\} Π_{i}^{- 1} E \{ε_{i} {ε^{T}}_{j}\} \end{matrix} \end{matrix}$ （22）

由于l=j+1≤ q, 有j≤ q-1。当k=q-1时, 式(20)成立, 因此期望E{ε _i $\begin{matrix} {ε^{T}}_{j} \end{matrix}$ }, i=1, 2, …, j-1为0, 所以有:

$\begin{matrix} E \{ε_{l} {ε^{T}}_{j}\} = {\bar{D}}_{j + 1} E \{v_{j + 1} {ε^{T}}_{j}\} - {\bar{D}}_{j + 1} R_{j + 1, j} {\bar{D}}^{T}_{j} (23) \end{matrix}$

式中:期望E{v_j+₁ $\begin{matrix} {ε^{T}}_{j} \end{matrix}$ }可计算如下:

$\begin{matrix} \begin{matrix} E \{v_{j + 1} {ε^{T}}_{j}\} = E \{v_{j + 1} (y_{j} - {\bar{C}}_{j} {\hat{x}}_{j | j - 1} - {\bar{D}}_{j} \times \\ R_{j, j - 1} {\bar{D}}^{T}_{j - 1} Π_{j - 1}^{- 1} {ε_{j - 1}}^{T} = \\ E \{v_{j + 1} {(C_{j} x_{j} + D_{j} v_{j})}^{T}\} - \\ \overset{j - 1}{\sum_{i = 1}} E \{v_{j + 1} {ε^{T}}_{i}\} Π_{i}^{- 1} E {\{x_{j} {ε^{T}}_{i}\}}^{T} {\bar{C}}^{T}_{j} - \\ E \{v_{j + 1} {ε^{T}}_{j - 1}\} {({\bar{D}}_{j} R_{j, j - 1} {\bar{D}}^{T}_{j - 1} Π_{j - 1}^{- 1})}^{T} \end{matrix} \end{matrix}$ （24）

根据引理3, 期望E $\begin{matrix} \{v_{j + 1} {ε^{T}}_{i}\} \end{matrix}$ , 1≤ i≤ j-1为0, 又由于系统状态x_j与测量噪声v_j+₁不相关, 测量噪声一步跨时自相关, 因此有

$\begin{matrix} E \{v_{j + 1} {ε^{T}}_{j}\} = R_{j + 1, j} {\bar{D}}^{T}_{j} (25) \end{matrix}$

将式(25)代入式(22), 可得E $\begin{matrix} \{ε_{l} {ε^{T}}_{j}\} \end{matrix}$ =0。

当p> 1, 由式(15)有:

$\begin{matrix} \begin{matrix} E \{ε_{l} {ε^{T}}_{j}\} = E \{(y_{j + p} - {\bar{C}}_{j + p} {\hat{x}}_{j + p | j + p - 1} - {\bar{D}}_{j + p} \times \\ R_{j + p, j + p - 1} {\bar{D}}^{T}_{j + p - 1} Π_{j + p - 1}^{- 1} ε_{j + p - 1} {ε^{T}}_{j} = \\ E \{(C_{j + p} x_{j + p} + D_{j + p} v_{j + p}) {ε^{T}}_{j}\} - {\bar{D}}_{j + p} \times \\ R_{j + p, j + p - 1} {\bar{D}}^{T}_{j + p - 1} Π_{j + p - 1}^{- 1} E \{ε_{j + p - 1} {ε^{T}}_{j}\} \times \\ {\bar{C}}_{j + p} \overset{j + p - 1}{\sum_{i = 1}} E \{x_{j + p} {ε^{T}}_{i}\} Π_{i}^{- 1} E \{ε_{i} {ε^{T}}_{j}\} \end{matrix} \end{matrix}$ （26）

由于l=j+p≤ q, 有j+p-1≤ q-1, j≤ q-p< q-1。在k=q-1时, 式(16)成立, 因此期望E{ε _i $\begin{matrix} {ε^{T}}_{j} \end{matrix}$ }, i=1, 2, …, j-1, j+1, …, j+p-1为0。因此有:

$\begin{matrix} E \{ε_{l} {ε^{T}}_{j}\} = {\bar{D}}_{j + p} E \{v_{j + p} {ε^{T}}_{j}\} (27) \end{matrix}$

又由于p> 1, 根据引理3, 期望E{v_j+p $\begin{matrix} {ε^{T}}_{j} \end{matrix}$ }为0。因此期望E{ε _l $\begin{matrix} {ε^{T}}_{j} \end{matrix}$ }为0。证毕

下面用一个定理来完成滤波器的设计。

定理1 对于系统(6)(7), 有下面的递推鲁棒滤波器:

$\begin{matrix} \begin{matrix} {\hat{x}}_{k | k - 1} = A_{k - 1} {\hat{x}}_{k - 1 | k - 1} (28) \\ P_{k | k - 1} = A_{k - 1} P_{k - 1 | k - 1} {A^{T}}_{k - 1} + \\ A_{s, k - 1} X_{k - 1} {A^{T}}_{s, k - 1} + B_{k - 1} Q_{k - 1} {B^{T}}_{k - 1} (29) \\ {\hat{x}}_{k | k} = {\hat{x}}_{k | k - 1} + Ξ_{k} Π_{k}^{- 1} ε_{k} (30) \\ P_{k | k} = P_{k | k - 1} - Ξ_{k} Π_{k}^{- 1} {Ξ^{T}}_{k} (31) \\ Ξ_{k} = P_{k | k - 1} {\bar{C}}^{T}_{k} - A_{k - 1} Ξ_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} {\bar{D}}^{T}_{k} (32) \\ Π_{k} = {\bar{C}}_{k} P_{k | k - 1} {\bar{C}}^{T}_{k} + σ_{k}^{2} C_{e, k} X_{k} {C^{T}}_{e, k} + \\ {\bar{D}}_{k} R_{k} {\bar{D}}^{T}_{k} + σ_{k}^{2} D_{e} R_{k} {D^{T}}_{e} - \\ {\bar{C}}_{k} A_{k - 1} Ξ_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} {\bar{D}}^{T}_{k} - \\ {\bar{D}}_{k} {(A_{k - 1} Ξ_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1})}^{T} {\bar{C}}^{T}_{k} - \\ {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} {\bar{D}}^{T}_{k} (33) \\ ε_{k} = y_{k} - {\bar{C}}_{k} {\overset{^{}}{x}}_{k | k - 1} - {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} ε_{k - 1} (34) \end{matrix} \end{matrix}$

式中:Ξ _k是新息与系统状态乘积的数学期望; 矩阵X_k是如引理2所示的状态乘积的数学期望; P_k|k和P_k|k-₁是系统估计和一步预测的误差协方差矩阵; $\begin{matrix} {\hat{x}}_{k | k} \end{matrix}$ 是系统状态在k时刻的滤波值; 滤波器初值为: $\begin{matrix} {\hat{x}}_{0 | 0} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} {\bar{\overset{⌒}{x}}}_{0} & 0 \end{matrix}]}^{T} \end{matrix}$ , P₀_|₀=diag( $\begin{matrix} {\overset{⌒}{P}}_{0} \end{matrix}$ , 0), ε ₁=y₁。

证明:根据新息分析和垂直投影定理, 系统状态的一步预测可计算如下:

$\begin{matrix} {\hat{x}}_{k | k - 1} = \overset{k - 1}{\sum_{i = 1}} E \{x_{k} {ε^{T}}_{i}\} Π_{i}^{- 1} ε_{i} = A_{k - 1} {\hat{x}}_{k - 1 | k - 1} \end{matrix}$ （35）

因此一步预测误差 $\begin{matrix} {\tilde{x}}_{k | k - 1} \end{matrix}$ 有下面的形式:

$\begin{matrix} {\tilde{x}}_{k | k - 1} = x_{k} - {\hat{x}}_{k | k - 1} = A_{k - 1} {\tilde{x}}_{k - 1 | k - 1} + A_{s, k - 1} η_{k - 1} x_{k - 1} + B_{k - 1} ω_{k - 1} \end{matrix}$ (36)

式中: $\begin{matrix} {\tilde{x}}_{k - 1 | k - 1} \end{matrix}$ 是k-1时刻的状态估计误差。进而一步预测的误差协方差可计算如下:

$\begin{matrix} \begin{matrix} P_{k | k - 1} = E \{{\tilde{x}}_{k | k - 1} {\tilde{x}}^{T}_{k | k - 1}\} = \\ E \{(A_{k - 1} {\tilde{x}}_{k - 1 | k - 1} + A_{s, k - 1} η_{k - 1} x_{k - 1} + B_{k - 1} ω_{k - 1}) \times \\ {(A_{k - 1} {\tilde{x}}_{k - 1 | k - 1} + A_{s, k - 1} η_{k - 1} x_{k - 1} + B_{k - 1} ω_{k - 1})}^{T} = \\ A_{k - 1} P_{k - 1 | k - 1} {A^{T}}_{k - 1} + \\ A_{s, k - 1} X_{k - 1} {A^{T}}_{s, k - 1} + B_{k - 1} Q_{k - 1} {B^{T}}_{k - 1} \end{matrix} \end{matrix}$ (37)

应用垂直投影定理, 状态估计 $\begin{matrix} {\hat{x}}_{k | k} \end{matrix}$ 可计算如下:

$\begin{matrix} {\hat{x}}_{k | k} = \overset{k}{\sum_{i = 1}} E \{x_{k} {ε^{T}}_{i}\} Π_{i}^{- 1} ε_{i} = {\hat{x}}_{k | k - 1} + Ξ_{k} Π_{k}^{- 1} ε_{k} \end{matrix}$ （38）

式中:期望Ξ _k和新息均方值Π _k有如下的计算形式:

$\begin{matrix} \begin{matrix} Ξ_{k} = E \{x_{k} (y_{k} - {\bar{C}}_{k} {\hat{x}}_{k | k - 1} \\ - {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} {ε_{k - 1}}^{T} = \\ E \{x_{k} {\tilde{x}}^{T}_{k | k - 1}\} {\bar{C}}^{T}_{k} + E \{x_{k} {x^{T}}_{k}\} E \{{\bar{C}}^{T}_{k} +\} \\ E \{x_{k} {v^{T}}_{k}\} {\bar{D}}^{T}_{k} - E \{x_{k} {ε^{T}}_{k - 1}\} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} {\bar{D}}^{T}_{k} \end{matrix} \end{matrix}$ （39）

测量噪声与状态不相关, 因此E $\begin{matrix} \{x_{k} {v^{T}}_{k}\} \end{matrix}$ 为0; 由矩阵 $\begin{matrix} {\tilde{C}}^{T}_{k} \end{matrix}$ 的定义可知期望E $\begin{matrix} \{{\bar{C}}^{T}_{k}\} \end{matrix}$ 为0; 根据引理4可知 $\begin{matrix} {\hat{x}}_{k | k - 1} \end{matrix}$ 与 $\begin{matrix} {\tilde{x}}_{k | k - 1} \end{matrix}$ 垂直, 进而有:

$\begin{matrix} \begin{matrix} Ξ_{k} = E \{{\tilde{x}}_{k | k - 1} {\tilde{x}}^{T}_{k | k - 1}\} {\bar{C}}^{T}_{k} - E \{(A_{k - 1} x_{k - 1} + A_{s, k - 1} η_{k - 1} \times \\ x_{k - 1} + B_{k - 1} ω_{k - 1} {ε^{T}}_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} {\bar{D}}^{T}_{k} = \\ P_{k | k - 1} {\bar{C}}^{T}_{k} - A_{k - 1} Ξ_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} {\bar{D}}^{T}_{k} \end{matrix} \end{matrix}$ （40）

考虑到测量噪声是一步跨时自相关, 有:

$\begin{matrix} \begin{matrix} Π_{k} = E \{({\bar{C}}_{k} {\tilde{x}}_{k | k - 1} + {\tilde{C}}_{k} x_{k} + D_{k} v_{k} - {\bar{D}}_{k} R_{k, k - 1} \times \\ {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} ε_{k - 1} ({\bar{C}}_{k} {\tilde{x}}_{k | k - 1} + {\tilde{C}}_{k} x_{k} + D_{k} v_{k} - \\ {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} {ε_{k - 1}}^{T} = \\ {\bar{C}}_{k} P_{k | k - 1} {\bar{C}}^{T}_{k} + {\bar{C}}_{k} E \{{\tilde{x}}_{k | k - 1} {v^{T}}_{k}\} {\bar{D}}^{T}_{k} + \\ E \{{\tilde{C}}_{k} x_{k} {x^{T}}_{k} {\tilde{C}}^{T}_{k}\} + {\bar{D}}_{k} E \{v_{k} {\tilde{x}}^{T}_{k | k - 1}\} {\bar{D}}^{T}_{k} + \\ E \{D_{k} v_{k} {v^{T}}_{k} {D^{T}}_{k}\} - \\ {\bar{D}}_{k} R_{k, k - 1} {\bar{D}}^{T}_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} {\bar{D}}^{T}_{k} \end{matrix} \end{matrix}$ （41）

根据式(25), 引理1, 引理2和引理3, 式(41)中期望可计算如下:

$\begin{matrix} \begin{matrix} E \{{\tilde{x}}_{k | k - 1} {v^{T}}_{k}\} = - A_{k - 1} Ξ_{k - 1} Π_{k - 1}^{- 1} {\bar{D}}_{k - 1} {R^{T}}_{k, k - 1} (42) \\ E \{{\tilde{C}}_{k} x_{k} {x^{T}}_{k} {\tilde{C}}^{T}_{k}\} = E \{J_{k} C_{e, k} x_{k} {x^{T}}_{k} {C^{T}}_{e, k} {J^{T}}_{k}\} = \\ σ_{k}^{2} C_{e, k} X_{k} {C^{T}}_{e, k} (43) \\ E \{D_{k} v_{k} {v^{T}}_{k} {D^{T}}_{k}\} = E \{({\bar{D}}_{k} + {\tilde{D}}_{k}) v_{k} {v^{T}}_{k} ({\bar{D}}_{k} + {\tilde{D}}_{k})\} = \\ {\bar{D}}_{k} R_{k} {\bar{D}}^{T}_{k} + σ_{k}^{2} D_{e} R_{k} {D^{T}}_{e} (44) \end{matrix} \end{matrix}$

将式(42)~(44)代入到式(41), 可得式(33)。

由式(6)和式(37), 估计误差 $\begin{matrix} {\tilde{x}}_{k | k} \end{matrix}$ 可计算如下:

$\begin{matrix} {\tilde{x}}_{k | k} = x_{k} - {\hat{x}}_{k | k - 1} - Ξ_{k} Π_{k}^{- 1} ε_{k} = {\tilde{x}}_{k | k - 1} - Ξ_{k} Π_{k}^{- 1} ε_{k} \end{matrix}$ (45)

由式(44), 估计误差协方差P_k|k可计算如下:

$\begin{matrix} \begin{matrix} P_{k | k} = E \{({\tilde{x}}_{k | k - 1} - Ξ_{k} Π_{k}^{- 1} ε_{k}) {({\tilde{x}}_{k | k - 1} - Ξ_{k} Π_{k}^{- 1} ε_{k})}^{T}\} = \\ P_{k | k - 1} - E \{{\tilde{x}}_{k | k - 1} {ε^{T}}_{k}\} Π_{k}^{- 1} {Ξ^{T}}_{k} - Ξ_{k} Π_{k}^{- 1} \times \\ E \{ε_{k} {\tilde{x}}^{T}_{k | k - 1}\} + Ξ_{k} Π_{k}^{- 1} {Ξ^{T}}_{k} \end{matrix} \end{matrix}$ (46)

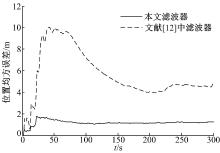
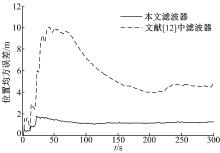
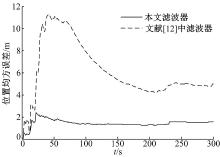
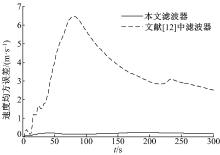
根据引理4, 可得期望E $\begin{matrix} \{ε_{k} {\tilde{x}}^{T}_{k | k - 1}\} \end{matrix}$ =Ξ _k, 将其代入式(46), 可得式(31)。证毕

本节利用新息分析和垂直投影定理完成了递推鲁棒滤波器的设计。新的滤波器与卡尔曼滤波器在形式上的不同主要体现在式(29)和式(32)~(34)上。而这些不同是由系统模型参数随机不确定性和测量信息在传输中出现的随机时滞所造成。也正是这些不同构成了本文所得到的递推鲁棒滤波方法与传统卡尔曼滤波方法的区别。另一方面, 定理1处理的是一个维数为2n的系统, 而传统的将跨时相关性噪声进行增广的方法需要处理一个维数为2n+2m的系统, 因此定理1得到的滤波器具有更小的计算复杂度。另一方面定理1得到的是一个递推滤波器, 相对于传统的非递推形式更容易实时的在线计算。

注释2:文献[14]研究了具有测量丢失现象和相关性噪声的随机非线性不确定系统的最优滤波问题。与文献[14]相比, 本文则研究了具有测量时滞现象的随机不确定性系统的递推鲁棒滤波问题; 在获得所期望滤波器的同时, 对于新得到的新息之间的不相关性本文也给出了严格的数学证明; 在技术途径方面, 本文不但应用了新息分析, 还应用了垂直射影定理和数学归纳法。

3 仿真计算

接下来, 将定理1得到的滤波器应用到下面的二阶目标追踪系统:

$\begin{matrix} \begin{matrix} {\overset{⌒}{x}}_{k + 1} = ([\begin{matrix} 1 & τ \\ 0 & 1 \end{matrix}] + [\begin{matrix} 0.1 & 0 \\ 0 & 0.1 \end{matrix}] η_{k}) {\overset{⌒}{x}}_{k} + [\begin{matrix} τ^{2} / 2 \\ τ \end{matrix}] ω_{k} (47) \\ {\overset{⌒}{y}}_{k} = {[\begin{matrix} 1 & 1 \end{matrix}]}^{T} {\overset{⌒}{x}}_{k} + {\overset{⌒}{v}}_{k} (48) \\ y_{k} = (1 - λ_{k}) {\overset{⌒}{y}}_{k} + λ_{k} {\overset{⌒}{y}}_{k - 1} (49) \end{matrix} \end{matrix}$

式中:τ 是采样周期; $\begin{matrix} {\overset{⌒}{x}}_{k} \end{matrix}$ = $\begin{matrix} [\begin{matrix} s_{k} & {\overset{\cdot}{s}}_{k} \end{matrix}] \end{matrix}$ 是目标的位置与速度; $\begin{matrix} {\overset{⌒}{y}}_{k} \end{matrix}$ 是传感器测量; y_k是最终计算的测量; λ _k是概率已知的随机伯努利序列, 取其概率特性为Prob $\begin{matrix} \{λ_{k} = 1\} \end{matrix}$ =β _k= $\begin{matrix} \{\begin{matrix} 0.1, & 0.2 \end{matrix}\} \end{matrix}$ ; ω _k、 $\begin{matrix} {\overset{⌒}{v}}_{k} \end{matrix}$ 和η _k是互不相关的单位方差零均值噪声。

系统采样周期为τ =0.1 s, 系统初值假设为 $\begin{matrix} {\overset{⌒}{x}}_{0} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} 20 & 1 \end{matrix}]}^{T} \end{matrix}$ , $\begin{matrix} {\overset{⌒}{P}}_{0} \end{matrix}$ =diag $\begin{matrix} (\begin{matrix} 5 & 1 \end{matrix}) \end{matrix}$ , $\begin{matrix} {\overset{⌒}{y}}_{- 1} \end{matrix}$ =0。图1~图4是仿真结果, 从仿真图上可以看到, 无论是对位置还是对速度的估计, 定理1得到的滤波器都具有更高的精度。原因在于文献[12]将噪声作为目标系统的一部分来进行估计, 正如文献[13]分析的, 对噪声很难实现精准估计, 而低精度的噪声估计又将降低整个目标系统的估计精度。

	Figure Option View Download New Window
	图1 位置误差比较(β _k=0.1)Fig.1 Comparison of positional error(β _k=0.1)

	Figure Option View Download New Window
	图2 速度误差比较(β _k=0.1)Fig.2 Comparison of velocity error(β _k=0.1)

	Figure Option View Download New Window
	图3 位置误差比较(β _k=0.2)Fig.3 Comparison of positional error(β _k=0.2)

	Figure Option View Download New Window
	图4 速度误差比较(β _k=0.2)Fig.4 Comparison of velocity error(β _k=0.2)

4 结束语

针对系统中出现的测量信息传输过程中产生的时间延迟和模型参数的随机乘性不确定性, 设计了基于垂直投影定理的递推鲁棒滤波器。滤波器设计思路是:用伯努利序列来描述测量数据传输时滞, 系统参数的不确定性描述成一个乘性噪声, 接着将原系统转化成为一个含跨时相关性噪声的随机参数不确定性系统, 然后重新计算了新息, 并用数学归纳法证明了所得到的新息是一个互不相关的序列, 在此基础上, 利用新息分析和垂直投影定理得到了所期望的递推鲁棒滤波器。与传统的方法相比, 本文对跨时相关性噪声的处理不需要进行状态的增广, 因而计算量小, 估计精度高, 并且所得到的鲁棒滤波器具有递推形式, 因而更加合适于在线实时计算, 仿真结果也验证了该方法的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	姚郁, 刘富春, 贺风华. 基于LMI的范数有界不确定采样系统的输出反馈鲁棒镇定[J]. 吉林大学学报: 工学版, 2009, 39(6): 1568-1572. Yao Yu, Liu Fu-chu, He Feng-hua. LMI-based output feedback robust stabilization for sampled -data systems wit norm-bounded uncertainties[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(6): 1568-1572. [本文引用:1]
[2]	冯建鑫, 王挺峰, 郭劲. 测量丢失不确定性系统的迭代鲁棒滤波[J]. 吉林大学学报: 工学版, 2014, 44(4): 1057-1061. Feng Jian-xin, Wang Ting-feng, Guo Jin. Iterative robust filtering for uncertain systems with missing measurements[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(4): 1057-1061. [本文引用:1]
[3]	Feng J X, Wang Z D, Zeng M. Optimal robust non-fragile Kalman-type recursive filtering with finite-step correlated noises and multiple packet dropouts[J]. Aerospace Science and Technology, 2011, 15(6): 486-494. [本文引用:1]
[4]	Yang F W, Wang Z D, Hung Y S. Robust kalman filtering for discrete time-varying uncertain systems with multiplicative noises[J]. IEEE Transactions on Automatic Control, 2002, 47(7): 1179-1183. [本文引用:1]
[5]	Phillis Y A. Estimation and control of systems with unknown covariance and multiplicative noise[J]. IEEE Transactions on Automatic Control, 1989, 34(10): 1075-1078. [本文引用:1]
[6]	Tekalp A M, Pavloviv G. Image restoration with multiple noise: incorporating the sensor nonlinearity[J]. IEEE Transactions on Signal Processing, 1991, 39(9): 2132-2136. [本文引用:1]
[7]	冯建鑫. 含相关性噪声的估计和融合算法研究[D]. 哈尔滨: 哈尔滨工业大学航天学院, 2012. Feng Jian-xin. Study on estimation and fusion algorithm for systems with correlated noises[D]. Harbin: School of Astronautics, Harbin Institute of Technology, 2012. [本文引用:1]
[8]	Feng J X, Wang Z D, Zeng M. Distributed weighted robust Kalman filter fusion for uncertain systems with autocorreated and cross-correlated noises[J]. Information Fusion, 2013, 14(1): 78-86. [本文引用:2]
[9]	Feng J X, Wang T F, Guo J. Recursive estimation for descriptor systems with multiple packet dropouts and correlated noises[J]. Aerospace Science and Technology, 2014, 32(1): 200-211. [本文引用:2]
[10]	Liu X, Zhang H, Wang W, et al. Kalman filtering for multiple time-delay systems[J]. Automatica, 2005, 41(8): 1455-1461. [本文引用:1]
[11]	Yaz E, Ray A. Linear unbiased state estimation under rand omly varying bounded sensor delay[J]. Applied Mathematical Letters, 1998, 11(4): 27-32. [本文引用:1]
[12]	Wen C H, Liu R L, Chen T W. Linear unbiased state estimation with rand om one-step sensor delay[J]. Circuits Systems and Signal Processing, 2007, 26(4): 573-590. [本文引用:1]
[13]	Feng J X, Zeng M. Descriptor recursive estimation for multiple sensors with different delay rates[J]. International Journal of Control, 2011, 84(3): 584-596. [本文引用:1]
[14]	Zhang S, Zhao Y, Li M, et al. Optimal filtering for uncertain systems with stochastic nonlinearities, correlated noises and missing measurements[J]. Journal of Systems Engineering and Electronics, 2015, 26(5): 1052-1059. [本文引用:1]

2009

0.0

. 2009, 39(6):1568-1572

LMI-based output feedback robust stabilization for sampled -data systems wit norm-bounded uncertainties

基于LMI的范数有界不确定采样系统的输出反馈鲁棒镇定

Yao Yu , Liu Fu-chu , He Feng-hua.

姚郁, 刘富春, 贺风华

摘　要：将采样控制系统转化为等价的跳变系统,设计目标为对所有容许的参数不确定性设计一个输出反馈采样控制器,使得闭环系统渐近稳定。以线性矩阵不等式的形式给出了鲁棒镇定问题可解的充分条件,并由可行解构造输出反馈采样控制器的参数矩阵。对短周期飞行器动态模型的仿真结果验证了所提方法的有效性和正确性。

... 0 引言卡尔曼滤波理论自诞生之初便广泛应用于航空航天和信号处理等军事及民用领域^[1,2] ...

2014

0.0

. 2014, 44(4):1057-1061

Iterative robust filtering for uncertain systems with missing measurements

测量丢失不确定性系统的迭代鲁棒滤波

Feng Jian-xin , Wang Ting-feng , Guo Jin.

冯建鑫, 王挺峰, 郭劲

... 0 引言卡尔曼滤波理论自诞生之初便广泛应用于航空航天和信号处理等军事及民用领域^[1,2] ...

2011

0.0

... 模型参数不确定性的种类很多,乘性噪声作为模型随机不确定性的重要一类广泛存在于航空航天、无线电通信传输等领域^[3,4] ...

2002

0.0

... 模型参数不确定性的种类很多,乘性噪声作为模型随机不确定性的重要一类广泛存在于航空航天、无线电通信传输等领域^[3,4] ...

1989

0.0

... 目前为止,国内外学者在含乘性噪声的随机动态滤波器和控制器设计上做了不少工作形成了包括基于game理论和线性矩阵不等式等的研究方法^[5,6] ...

1991

0.0

... 目前为止,国内外学者在含乘性噪声的随机动态滤波器和控制器设计上做了不少工作形成了包括基于game理论和线性矩阵不等式等的研究方法^[5,6] ...

2012

0.0

. 2012, :-

Study on estimation and fusion algorithm for systems with correlated noises[D]. Harbin: School of Astronautics,

含相关性噪声的估计和融合算法研究[D]

Feng Jian-xin.

冯建鑫

实际应用中，动态系统的外界干扰通常不是互不相关的高斯白噪声，因而，相关性噪声滤波是最优估计理论研究的一个热点并且在近些年得到广大学者的普遍关注。网络的广泛应用推动了相关性噪声滤波理论的发展，对网络产生的时滞、丢包等估计问题的研究在大多数情况下可以转化成对含相关性噪声的随机动态系统的估计问题的研究。另外，传感器技术的发展也同样影响着估计理论的发展，对含相关性噪声系统的多传感器数据融合问题的研究也得到了越来越多的关注。除此之外，系统模型不确定性是估计器估计效果变坏甚至不稳定的重要因素。然而，由于人们认知的局限性以及系统本身和环境的变化，使得所建立的系统数学模型与实际系统之间总会有偏差。因此，不确定系统的鲁棒滤波理论也就成了当前估计理论研究的另外一个热点。本文在总结前人研究的基础上，研究了含相关性噪声，模型不确定性和测量数据时滞、丢失现象的动态系统的估计和融合问题，并将所得到的部分理论结果应用到恒定速度的目标追踪系统和恒定加速度的目标追踪系统。本文的主要工作可概括如下：针对动态系统中存在的有限步跨时自相关过程噪声，模型不确定性和测量数据丢失现象提出了最小方差最优的递推鲁棒滤波器设计方法。综合考虑了动态方程和测量方程中的随机不确定性；过程噪声是有限步跨时自相关的；测量数据丢失现象被描述成一个二进制切换序列。基于最小方差最优的设计思路，得到了所期望的鲁棒滤波器。最后，数字仿真结果表明了所设计的滤波器具有良好的工作性能。提出了含有限步跨时自相关测量噪声，模型不确定性和多包丢失现象的动态系统的最优非脆弱滤波器设计方法。不但考虑了系统模型中存在的不确定性，而且还考虑了所设计的滤波器参数的不确定性。基于一个多包丢失模型和状态向量增广，得到了一个含有限步跨时自相关和互相关噪声的随机不确定系统。在最小方差意义下，得到了所期望的最优非脆弱滤波器。最后，仿真计算验证了所设计滤波器的有效性。将测量数据传输中出现的时滞、丢包等现象扩展到广义系统。提出了基于奇异值分解，革新分析和射影定理的广义滤波器，预测器和平滑器设计方法。基于奇异值分解和状态增广，原时滞广义系统的状态估计问题转化成含跨时相关性噪声的正常子系统和过程噪声的状态估计问题。基于革新分析法和射影定理，首先获得了子系统和过程噪声的滤波器，预测器和平滑器。在此基础上，最终获得了原广义系统的滤波器，预测器和平滑器。研究了含同时相关性噪声的动态系统的最优分布式卡尔曼滤波器融合算法。系统的过程噪声和每个传感器的测量噪声是同时刻相关，同时，每个传感器测量噪声之间也是同时刻相关。基于一个正交化的方法，原始测量转化成了测量噪声互不相关的新测量。基于新建测量，首先推导了不含反馈的最优分布式卡尔曼滤波融合算法，而后，推导了含反馈的最优分布式卡尔曼滤波融合算法。对于新得到的最优分布式卡尔曼滤波融合算法给出了严格的性能分析。最后，将得到的融合算法应用到恒定速度的目标追踪系统和恒定加速度的目标追踪系统，仿真结果表明了算法的有效性和性能分析的正确性。研究了含跨时相关性噪声的动态系统的分布式权重滤波融合。对于每个传感子系统，首先推导了局部的递推滤波器，在此基础上提出了应用分布式权重滤波融合方法来处理含跨时相关性噪声的动态系统的最优无偏融合问题。相对于其他的融合算法，新得到的融合算法有更强的抗干扰能力。最后，仿真计算验证了所设计融合算法的有效性。

... 随着网络技术的发展,网络广泛应用于控制和滤波领域^[7,8,9] ...

2013

0.0

... 随着网络技术的发展,网络广泛应用于控制和滤波领域^[7,8,9] ...

... Wen等^[12]利用将跨时相关性噪声进行状态增广的方法得到了一个最优线性滤波器,然而系统维数的增大必将带来沉重的计算负担,并且将噪声当成状态进行估计本身就是件困难的事情,很难进一步提高系统估计精度^[8,9,13],另外Wen等得到的滤波器非递推,计算时需占用较大内存 ...

2014

0.0

... 随着网络技术的发展,网络广泛应用于控制和滤波领域^[7,8,9] ...

2005

0.0

... Liu等^[10]将本质为随机时变的网络时滞现象描述为确定性时滞 ...

1998

0.0

... 针对这种情况,Yaz等^[11]应用一个已知概率的伯努利分布序列来描述这类网络时滞现象,并在此模型基础上,Yaz设计了一个线性无偏滤波器 ...

2007

0.0

2011

0.0

2015

0.0