基于混沌多项式展开法的线束串扰统计模型

引用本文

王天皓, 王忠福, 王雨蒙, 杨开宇, 高印寒, 马喜来. 基于混沌多项式展开法的线束串扰统计模型. 吉林大学学报（工学版）, 2017, 47(5): 1568-1576
WANG Tian-hao, WANG Zhong-fu, WANG Yu-meng, YANG Kai-yu, GAO Yin-han, MA Xi-lai. Statistic analysis of cable bundle crosstalk based on polynomial chaos expansion. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1568-1576 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705032
Permissions

基于混沌多项式展开法的线束串扰统计模型

王天皓¹, 王忠福², 王雨蒙², 杨开宇², 高印寒², 马喜来³

1.吉林大学仪器科学与电气工程学院,长春 130061

2.吉林大学汽车仿真与控制国家重点实验室,长春130022

3.中国第一汽车股份有限公司技术中心,长春 130011

通信作者:杨开宇(1971-),男,副教授,博士.研究方向:汽车电子,电磁兼容及车辆测试技术.E-mail:yangky@jlu.edu.cn

作者简介:王天皓(1988-),男,在站博士后.研究方向:汽车电子,电磁兼容及车辆测试技术.E-mail:wangtianhao2006@126.com

基金项目:吉林省基础研究计划基金项目(20150101029JC)

摘要

针对线束导线在实际情况中为非确定性几何布置的这一问题,提出了一种基于混沌多项式展开法的线束串扰统计分析方法。该方法根据线束导线位置变量的分布类型选取相应的正交多项式对线束导线分布参数进行展开,结合边界条件,采用模式理论对基于混沌多项式展开的多导体传输线方程扩展形式进行求解,进而得到电压和电流向量的混沌多项式展开表达式,并利用混沌多项式展开法的相关性质得到表征线束串扰统计特征的相关参数。通过与传统的蒙特卡法进行对比可知,该方法在保证计算结果准确可靠的同时,计算效率也得到了大幅度的提高,从而实现复杂系统线束电磁兼容性能的高效预测。

关键词: 仪器仪表技术; 混沌多项式展开; 线束串扰; 多导体传输线; 统计分析

中图分类号:TM930.11 文献标志码:A 文章编号:1671-5497(2017)05-1568-09

Statistic analysis of cable bundle crosstalk based on polynomial chaos expansion

WANG Tian-hao¹, WANG Zhong-fu², WANG Yu-meng², YANG Kai-yu², GAO Yin-han², MA Xi-lai³

1.College of Instrumental & Electrical Engineering, Jilin University,Changchun 130061,China

2.State Key Laboratory of Automotive Simulation and Control, Jilin University,Changchun 130022,China

3.R&D Center, FAW Group Corporation, Changchun 130011,China

Abstract

For the phenomenon that the position of cable bundle in reality is non-deterministic geometric, this paper proposes the statistical analysis method of cable bundle crosstalk model based on Polynomial Chaos Expansion. The orthogonal polynomial basis functions are chosen based on the distribution pattern of the variables related to the positions of wires in the cable bundle, and the distributed parameters of the wires can be expressed by the Polynomial Chaos Expansion. With the boundary conditions, the extended MTL can be solved by the modeling methodology, and then the voltage vector and current vector can be expressed by the Polynomial Chaos Expansion. According to the properties of the Polynomial Chaos Expansion, the mean, standard deviation and variation range of the cable bundle crosstalk can be obtained, and the probability density function of the cable bundle crosstalk can also becalculatedthrough numerical method. Thus, the efficient prediction of electromagnetic compatibility of cable bundle in complex system has realized.

Key words: technology of instrument and meter; polynomial chaos expansion; cable bundle crosstalk; multi-conductor transmission lines; statistical analysis

Show Figures

0 引言

随着现代工业的不断发展, 越来越多的电气电子设备被广泛应用于飞机、舰艇、汽车等复杂系统中。线束作为系统中电路网络主体, 连接着各个电气电子部件, 并使之发挥功效。但其也为干扰信号的传播提供了载体, 不仅会提高临界设备及导线的噪声水平, 还会对系统的传导发射和辐射发射产生影响, 使得系统的整体电磁兼容性能剧烈下降^[1]。因此, 对于复杂系统的前期电磁兼容性设计, 线束导线串扰是其预测的首要任务^[2]。

在实际情况中, 由于线束在系统中的捆扎和安装方式具有一定的随机性, 以及系统所处的不同工作环境和工作状态(如飞机、舰艇、汽车的加速、减速、颠簸、振动等)都会导致线束导线的位置发生变化, 这使得线束导线表现为非确定性几何布置。美国肯塔基大学的PAUL通过实验发现, 串扰对线束导线的位置极为敏感, 由于线束导线之间位置的变化, 可导致串扰的变化高达20 dB^[3]。但由于计算线束导线串扰的传统电磁学方法, 如多导体传输线理论^{[4, 5]}, 时域有限差分法^{[6, 7]}, 矩量法^[8]等, 都是针对线束导线位置固定的理想情况进行计算, 对于非确定性几何布置的线束导线串扰计算, 其不仅会消耗大量的计算资源, 所获得的结果也并不理想。因此, 如何快速准确的描述出线束导线串扰的统计特性, 合理的预测线束导线串扰变化范围已成为了电磁兼容领域的研究热点。在目前已经开展的研究中, 主要有蒙特卡洛(Monte Carlo, MC)法^{[9, 10, 11]}、分形图学法^{[12, 13, 14]}、卷积法^{[15, 16]}、配置法^[17]、克里金法^[18], 以及其他一些统计学方法^{[19, 20, 21]}。但上述方法在计算线束导线串扰统计特性时, 普遍需要获得大量的线束导线在其横截面分布情况的样本, 存在计算效率低下的问题, 并不利于复杂系统线束导线串扰统计分析的工程应用。但上述方法在计算线束导线串扰统计特性时, 普遍需要获得大量的线束导线在其横截面分布情况的样本, 存在计算效率低下的问题, 并不利于复杂系统线束导线串扰统计分析的工程应用。

本文针对上述问题, 提出一种利用混沌多项式展开对线束导线串扰的统计特性进行快速预测的方法。首先, 根据与线束导线位置相关的参数分布类型和变化范围选定正交多项式的基函数, 再将线束导线分布参数进行混沌多项式展开, 同时获得各展开项所对应的系数。然后结合边界条件, 利用模式理论对扩展后的多导体传输线方程进行求解。并由混沌多项式展开的相关性质得到线束导线串扰的均值、标准差以及变化范围, 再利用数值方法得到某一频率下线束导线串扰的概率密度函数。最后通过与蒙特卡洛法的计算结果进行对比, 说明了PCE法在预测线束导线串扰的统计特性方面的准确性和高效性。

1 混沌多项式展开法的数学模型

混沌多项式展开法来源于Wiener^[22]所提出的同性混沌法, 它是一种严密高效的不确定分析方法, 具有很强的数学支撑。该方法利用正交多项式基对不确定变量进行展开, 通过正交多项式的性质, 将变量的随机特性转移至多项式系数上面。Wiener^[22]最初利用PCE法提出并建立了湍流计算模型。随后许多学者将该理论推广至其它工程领域, 如结构力学领域^{[23, 24]}, 环境与声场领域^[25], 随机差分方程领域^[26], 瞬态热传导领域^[27], 以及纳米材料电特性领域^[28]等方面。Wiener采用与高斯型随机变量对应的Hermite正交多项式为基函数对随机过程谱展开^[22]。其中Cameron-Martini定理证明了该展开能够以正交多项式的形式对任意随机过程进行描述^[29]。因此, 将以Hermite正交多项式为基函数的PCE法视为一种响应面模型, 利用原始模型所包含的一个或多个独立标准正态随机变量对其进行正交多项式混沌展开, 从而实现对该随机过程的不同阶精度近似表示。

假设原始模型为Y=y(ξ ), 其中ξ =[ξ ₁, ξ ₂, …, ξ _n]^T表示模型的n维相互独立的随机变量输入, 则模型的输出响应也能够利用ξ =[ξ ₁, ξ ₂, …, ξ _n]^T来表示。针对高斯随机过程, Wiener^[22]确定了以Hermite正交多项式为基函数进行混沌多项式展开的表达式:

$\begin{matrix} \begin{matrix} Y = a_{0} + \overset{n}{\sum_{i = 1}} a_{i} H_{1} (ξ_{i}) + \\ \overset{n}{\sum_{i = 1}} \overset{i}{\sum_{j = 1}} a_{ij} H_{2} (ξ_{i}, ξ_{j}) + \\ \overset{n}{\sum_{i = 1}} \overset{i}{\sum_{j = 1}} \overset{j}{\sum_{k = 1}} a_{ijk} H_{3} (ξ_{i}, ξ_{j}, ξ_{k}) + \dots \end{matrix} \end{matrix}$ (1)

式中:a₀、a_i、a_ij、a_ijk、…为待求解的确定性系数, H_p表示一个p阶Hermite正交多项。

对于一个n维p阶的Hermite正交多项式:H $\begin{matrix} \underset{p}{\underset{︷}{(ξ_{i}, \dots, ξ_{j})}} \end{matrix}$ (ξ _i, …, ξ _j∈ ξ ), 令ζ 表示H $\begin{matrix} \underset{p}{\underset{︷}{(ξ_{i}, \dots, ξ_{j})}} \end{matrix}$ 中所含的不同随机变量组成的向量, 则其表达式可写为:

$\begin{matrix} H_{p} (ζ) = e^{\frac{1}{2} ζ^{T} ζ} {(- 1)}^{n} \frac{\partial^{p}}{\partial ξ_{i} \dots \partial ξ_{j}} e^{- \frac{1}{2} ζ^{T} ζ} \end{matrix}$ (2)

将式(1)进行截断, 用p阶有限项来近似表达, 并设表达式共有m项, 则式(1)可简写为:

$\begin{matrix} Y = \overset{m - 1}{\sum_{i = 0}} {\hat{c}}_{i} φ_{i} (ξ) (3) \end{matrix}$

式中: $\begin{matrix} {\hat{c}}_{i} \end{matrix}$ (i=0, 1, …, m-1)为待求解的确定性展开系数, 与a₀、a_i、a_ij、a_ijk、…依次对应, φ _i(i=0, 1, …, m-1)为Hermite正交多项式, 可由式(2)计算获得, 它们是一组完备的正交基, 其满足:

$\begin{matrix} < φ_{i}, φ_{j} > = < φ_{i}^{2} > δ_{ij} (4) \end{matrix}$

式中:δ _ij为克罗内克函数, < · , · > 为希尔伯特空间下的内积, 此处可将其定义为:

$\begin{matrix} < φ_{i}, φ_{j} > = \int φ_{i} (ξ) φ_{j} (ξ) W (ξ) dξ (5) \end{matrix}$

式(5)中W(ξ )为正交多项式基φ _i所对应的权重函数。当正交多项式基φ _i为Hermite正交多项式时, 其权重函数表达式为n维正态分布函数:

$\begin{matrix} W (ξ) = \frac{\exp (- \frac{ξ^{T} ξ}{2})}{(\sqrt[]{2 π})} \end{matrix}$ （6）

对于待求解的确定性展开系数 $\begin{matrix} {\hat{c}}_{i} \end{matrix}$ , 可通过将已知确定性解投影到正交多项式基φ _i上来确定, 其表达式如下:

$\begin{matrix} {\hat{c}}_{i} = < y (ξ), φ_{i} (ξ) > / < φ_{i} {(ξ)}^{2} > (7) \end{matrix}$

当对式(3)进行多项式p阶截断时, 由于变量的维数为n, 则原始模型的正交多项式展开项数m可由式(8)求得:

$\begin{matrix} m = \frac{(p + n)!}{p! n!} \end{matrix}$ （8）

利用式(7)和式(8)可分别得到原始模型混沌多项式展开后的展开系数和展开项数, 根据Hermite正交多项式所具有的正交性, 原始模型对输入随机变量的响应均值Y_mean为^[30]:

$\begin{matrix} \begin{matrix} Y_{mean} = E_{PC} (Y (ξ)) = \int_{D_{ξ}} Y (ξ) W (ξ) dξ = \\ \int_{D_{ξ}} (\overset{m - 1}{\sum_{i = 0}} {\hat{c}}_{i} φ_{i} (ξ)) W (ξ) dξ = \\ {\hat{c}}_{0} \int_{D_{ξ}} φ_{0} (ξ) W (ξ) dξ + \\ \overset{m - 1}{\sum_{i = 1}} {\hat{c}}_{i} \int_{D_{ξ}} φ_{i} (ξ) W (ξ) dξ = \\ {\hat{c}}_{0} + \overset{m - 1}{\sum_{i = 1}} {\hat{c}}_{i} \int_{D_{ξ}} φ_{0} (ξ) φ_{i} (ξ) W (ξ) dξ = \\ {\hat{c}}_{0} \end{matrix} \end{matrix}$ （9）

式中:D_ξ为ξ 的积分域, 由上式可知, 模型的响应均值Y_mean为其混沌多项式展开的0阶展开项系数 $\begin{matrix} {\hat{c}}_{0} \end{matrix}$ 。利用相同的方法能够得到模型的响应方差Y_var为:

$\begin{matrix} \begin{matrix} Y_{var} = Va r_{PC} (Y (ξ)) = \\ E_{PC} [{(Y (ξ) - Y_{mean} (ξ))}^{2}] = \\ \int_{D_{ξ}} {(Y (ξ) - Y_{mean} (ξ))}^{2} W (ξ) dξ = \\ \int_{D_{ξ}} {(Y (ξ) - {\hat{c}}_{0})}^{2} W (ξ) dξ = \\ \int_{D_{ξ}} {(\overset{m - 1}{\sum_{i = 1}} {\hat{c}}_{i} φ_{i} (ξ))}^{2} W (ξ) dξ \\ \overset{m - 1}{\sum_{i = 1}} \overset{m - 1}{\sum_{j = 1}} \int_{D_{ξ}} {\hat{c}}_{i} φ_{i} (ξ) {\hat{c}}_{j} φ_{j} (ξ) W (ξ) dξ = \\ \overset{m - 1}{\sum_{i = 1}} [{\hat{c}}_{i}^{2} < φ_{i}^{2} >] \end{matrix} \end{matrix}$ （10）

2 基于混沌多项式展开法的线束导线串扰建模

2.1 线束模型的建立

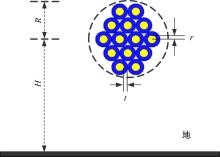
图1为符合德国大众汽车线缆标准的线束横截面。它包含14条导线, 线束半径R=4.5 mm, 线束中心距地高度为H=25 mm, 线束中导体材料为铜, 导体半径r=0.4 mm, 绝缘层材料为聚氯乙烯(PVC), 其相对介电常数为ε _r=3.0, 绝缘层厚度t=0.6 mm。线束长度L=1.25 m, 并假设线束导线为无耗若耦合。

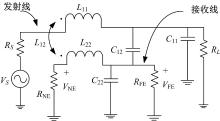
线束中发射线与接收线之间产生串扰的根本原因在于导线间的分布参数矩阵, 图2为发射线、接收线与地之间构成的三导体传输线等效电路模型。对于无耗传输线, 其分布参数矩阵分别为单位长度电感矩阵L和单位长度电容矩阵C, 其中, L的计算表达式为:

$\begin{matrix} \begin{matrix} L = [\begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix}] = \\ [\begin{matrix} \frac{μ_{0}}{2 π} \ln (\frac{2 h_{1}}{r_{1}}) & \frac{μ_{0}}{4 π} \ln (1 + 4 \frac{h_{1} h_{2}}{d^{2}}) \\ \frac{μ_{0}}{4 π} \ln (1 + 4 \frac{h_{1} h_{2}}{d^{2}}) & \frac{μ_{0}}{2 π} \ln (\frac{2 h_{2}}{r_{2}}) \end{matrix}] \end{matrix} \end{matrix}$ （11）

式中:μ ₀为真空磁导率; r₁和r₂分别为发射线和接收线的导体半径; h₁和h₂分别为发射线和接收线的对地高度; d为发射线和接收线之间的距离。

由于线束导线绝缘层的存在, 导体周围形成了非均匀介质。虽然它对单位长度电感矩阵L的影响可以忽略, 但对单位长度电容矩阵C会产生较大影响, 无法通过重要关系式LC=CL=μ ₀ε ₀计算获得。为了解决这一问题, 文献[31]利用镜像法原理推导得到了具有绝缘层的导线的单位长度电容矩阵C, 其表达式为:

$\begin{matrix} \begin{matrix} C = [\begin{matrix} C_{11} + C_{12} & - C_{12} \\ - C_{21} & C_{22} + C_{12} \end{matrix}] = \\ {[\begin{matrix} \frac{1}{2 π ε_{0}} (\frac{1}{ε_{r}} \ln \frac{1}{r_{1}} + ε_{e} \ln \frac{1}{r_{1} + t_{1}} - \ln \frac{1}{2 h_{1}}) & \frac{1}{4 π ε_{0}} \ln (1 + \frac{4 h_{1} h_{2}}{d^{2}}) \\ \frac{1}{4 π ε_{0}} \ln (1 + \frac{4 h_{1} h_{2}}{d^{2}}) & \frac{1}{2 π ε_{0}} (\frac{1}{ε_{r}} \ln \frac{1}{r_{2}} + ε_{e} \ln \frac{1}{r_{2} + t_{2}} - \ln \frac{1}{2 h_{2}}) \end{matrix}]}^{- 1} \end{matrix} \end{matrix}$ （12）

式中:ε ₀为真空介电常数; ε _r为相对介电常数; ε _e=(ε _r-1)/ε _r为有效介电常数; t₁和t₂分别为发射线和接收线的绝缘层厚度。

	Figure Option View Download New Window
	图1 线束横截面模型Fig.1 Cross section model of cable bundies

	Figure Option View Download New Window
	图2 三导体传输线等效电路模型Fig.2 Conductor transmission line crosstalk equivaient circuit model

2.2 线束导线分布参数的混沌多项式展开

由式(11)和(12)可知, 当线束的型号确定后, 分布参数矩阵各元素的大小取决于线束导线的几何位置, 即发射线对地高度h₁, 接收线对地高度h₂, 以及发射线和接收线之间的距离d, 假设上述三个参数为符合正态分布的相互独立的随机变量。为了采用以Hermite正交多项式为基函数对分布参数矩阵进行展开, 需要将上述三个符合正态分布的随机变量利用标准正态分布变量表示如下:

$\begin{matrix} \{\begin{matrix} h_{1} = {\bar{h}}_{1} + σ_{1} ξ_{1} \\ h_{2} = {\bar{h}}_{2} + σ_{2} ξ_{2} \\ d = \bar{d} + σ_{3} ξ_{3} \end{matrix} \end{matrix}$ （13）

式中: $\begin{matrix} {\bar{h}}_{1} \end{matrix}$ 、 $\begin{matrix} {\bar{h}}_{2} \end{matrix}$ 和 $\begin{matrix} \bar{d} \end{matrix}$ 分别表示3个导线位置参数的均值; σ ₁、σ ₂和σ ₃分别表示3个导线位置参数的标准差; ξ ₁、ξ ₂和ξ ₃为3个符合标准正态分布的随机变量。对于标准正态分布变量, 99.7%的数值分布在距离均值3个标准差之内的范围, 故结合图1所示的线束横截面模型和式(14)可得, $\begin{matrix} {\bar{h}}_{1} \end{matrix}$ = $\begin{matrix} {\bar{h}}_{2} \end{matrix}$ =25 mm, $\begin{matrix} \bar{d} \end{matrix}$ =4.5 mm, σ ₁=σ ₂=1.3 mm, σ ₃=1.1 mm。

接下来利用混沌多项式展开法对单位长度电感矩阵L和单位长度电容矩阵C进行展开, 可将其表示为:

$\begin{matrix} L = \overset{m - 1}{\sum_{i = 0}} L_{i} φ_{i} (ξ), C = \overset{m - 1}{\sum_{i = 0}} C_{i} φ_{i} (ξ) (14) \end{matrix}$

式中:ξ 为3维随机序列, ξ =[ξ ₁, ξ ₂, ξ ₃]^T; {L_i}和{C_i}为正交多项式{φ _i}所对应的系数。

本文仅以展开阶数p=1时为例, 对如何利用PCE法求解线束导线串扰的统计特性进行说明, 由式(8)可知展开项数m=4, 利用式(2)能够获得Hermite正交多项式的表达式φ _i, 而利用式(5)可计算获得< $\begin{matrix} φ_{i}^{2} \end{matrix}$ > 的值, 如表1所示。

表1 三维随机变量的Hermite正交多项式2阶展开表 Table 1 Expansion terms and coefficients of three dimensional second order Hermite orthogonal Polynomials

序号i	阶数p	Hermite多项式φ _i	< $\begin{matrix} φ_{i}^{2} \end{matrix}$ >
0	0	1	1
1	1	ξ ₁	1
2	1	ξ ₂	1
3	1	ξ ₃	1

表1 三维随机变量的Hermite正交多项式2阶展开表 Table 1 Expansion terms and coefficients of three dimensional second order Hermite orthogonal Polynomials

对于分布参数矩阵中各元素的确定性展开系数 $\begin{matrix} {\hat{c}}_{_{(a, b), i}} \end{matrix}$ (包括C₍_a_,_b_),_i和L₍_a_,_b_),_i), 其中(a, b)表示该分布参数矩阵中元素的位置, 可由式(7)结合式(11)和式(12), 以及表1计算获得, 其表达式如下:

$\begin{matrix} {\hat{c}}_{_{(a, b)}, i} \end{matrix}$ = $\begin{matrix} \frac{\int_{R^{n}} \frac{{\hat{c}}_{(a, b)} (ξ) φ_{i} (ξ)}{\sqrt[]{{(2 π)}^{n}}} \exp (- \frac{1}{2} ξ^{T} ξ)}{< φ_{i}^{2} >} \end{matrix}$ (15)

表2为利用式(15)得到的分布参数矩阵各元素的Hermite正交多项式展开系数。

表2 C和L基于Hermite正交多项式3阶展开各项系数(电感单位:H/m, 电容单位:F/m) Table 2 Each coefficients of L and C based on the third expansion of Hermite orthogonal polynomials

2.3 基于混沌多项式展开法的线束导线串扰统计模型的建立

无耗多导体传输线频域方程表达为:

$\begin{matrix} \{\begin{matrix} \frac{d}{dz} V (z, s) = - ZI (z, s) \\ \frac{d}{dz} I (z, s) = - YV (z, s) \end{matrix} \end{matrix}$ （16）

式中:电压向量V $\begin{matrix} (z) \end{matrix}$ 、电流向量I $\begin{matrix} (z) \end{matrix}$ , 以及单位长度阻抗矩阵Z和导纳矩阵Y分别为:

$\begin{matrix} \begin{matrix} V (z) = [\begin{matrix} V_{G} (z, s) \\ V_{R} (z, s) \end{matrix}], I (z) = [\begin{matrix} I_{G} (z, s) \\ I_{R} (z, s) \end{matrix}] (17) \\ Z = jωL, Y = jωC (18) \end{matrix} \end{matrix}$

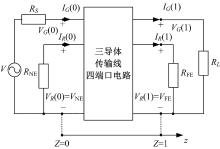
将图2所示的三导体传输线等效电路模型视为如图3所示的四端口电路, 当边界条件确定时, 根据戴维南定理可以将终端限定条件表示为:

$\begin{matrix} \{\begin{matrix} V (0) = V_{S} - Z_{S} I (0) \\ V (l) = Z_{L} I (l) \end{matrix} \end{matrix}$ （19）

式中:激励源V_S= $\begin{matrix} {[V_{S}, 0]}^{T} \end{matrix}$ , 源端阻抗矩阵Z_S=diag $\begin{matrix} ([R_{S}, R_{NE}]) \end{matrix}$ , 负载端阻抗矩阵Z_L=diag $\begin{matrix} ([R_{L}, R_{FE}]) \end{matrix}$ 。

	Figure Option View Download New Window
	图3 三导体传输线的四端口电路Fig.3 Four port circuit of three conductor transmission line

由上述已知条件, 利用模式理论^[32]可分别求得近端串扰电压V_NE和远端串扰电压V_FE等参数。

为了获得线束导线串扰的统计模型, 将电压向量V $\begin{matrix} (z) \end{matrix}$ 和电流向量I $\begin{matrix} (z) \end{matrix}$ 利用混沌多项式展开为:

$\begin{matrix} \{\begin{matrix} V (z, s) = \overset{m - 1}{\sum_{i = 0}} V_{i} φ_{i} (ξ) \\ I (z, s) = \overset{m - 1}{\sum_{i = 0}} I_{i} φ_{i} (ξ) \end{matrix} \end{matrix}$ （20）

再将式(14)、式(18)和式(20)代入式(16)所示的多导体传输线方程中得:

$\begin{matrix} \begin{matrix} \frac{d}{dz} \overset{m - 1}{\sum_{i = 0}} V_{i} (z, s) φ_{i} (ξ) = \\ - jω \overset{m - 1}{\sum_{i = 0}} \overset{m - 1}{\sum_{j = 0}} C_{i} I_{j} (z, s) φ_{i} (ξ) φ_{j} (ξ) \\ \frac{d}{dz} \overset{m - 1}{\sum_{i = 0}} I_{i} (z, s) φ_{i} (ξ) = \\ - jω \overset{m - 1}{\sum_{i = 0}} \overset{m - 1}{\sum_{j = 0}} L_{i} V_{j} (z, s) φ_{i} (ξ) φ_{j} (ξ) \end{matrix} \end{matrix}$ （21）

对式(21)做内积运算, 可以得到关于多导体传输线的一系列微分方程, 其表达式为:

$\begin{matrix} \{\begin{matrix} \forall a = 0, 1, \dots, m - 1 \\ \frac{d}{dz} \overset{m - 1}{\sum_{i = 0}} V_{i} (z, s) < φ_{i} (ξ), φ_{a} (ξ) > = \\ - jω \overset{m - 1}{\sum_{i = 0}} \overset{m - 1}{\sum_{j = 0}} C_{i} I_{j} (z, s) [φ_{i} (ξ) φ_{j} (ξ), φ_{a} (ξ)] \\ \frac{d}{dz} \overset{m - 1}{\sum_{i = 0}} I_{i} (z, s) < φ_{i} (ξ), φ_{a} (ξ) > = \\ - jω \overset{m - 1}{\sum_{i = 0}} \overset{m - 1}{\sum_{j = 0}} L_{i} V_{j} (z, s) < φ_{i} (ξ), φ_{a} (ξ) > \end{matrix} \end{matrix}$ (22)

经过整理、化简, 可将上式表示为:

$\begin{matrix} \{\begin{matrix} \frac{d}{dz} \tilde{V} (z, s) = - \tilde{C} \tilde{I} (z, s) \\ \frac{d}{dz} \tilde{I} (z, s) = - \tilde{L} \tilde{V} (z, s) \end{matrix} \end{matrix}$ （23）

式中:电压向量 $\begin{matrix} \tilde{V} \end{matrix}$ 和电流向量 $\begin{matrix} \tilde{I} \end{matrix}$ 中的元素个数扩大为原向量V和I的m倍, 而分布参数矩阵 $\begin{matrix} \tilde{C} \end{matrix}$ 和 $\begin{matrix} \tilde{L} \end{matrix}$ 的元素个数则扩大为原矩阵C和L的(m× m)倍。与此同时, 式(20)中的激励源V_S、源端阻抗矩阵Z_S、负载端阻抗矩阵Z_L的规模也相应地得到扩大。结合边界条件, 再次利用模式理论对式(24)求解可得近端串扰电压 $\begin{matrix} {\tilde{V}}_{NE} \end{matrix}$ 、电流 $\begin{matrix} {\tilde{I}}_{NE} \end{matrix}$ 以及远端串扰电压 $\begin{matrix} {\tilde{V}}_{FE} \end{matrix}$ 、电流 $\begin{matrix} {\tilde{I}}_{FE} \end{matrix}$ 等参数。

以近端串扰电压为例分析线束导线串扰的统计特性, 上述求得的近端串扰电压为 $\begin{matrix} {\tilde{V}}_{NE} \end{matrix}$ = $\begin{matrix} {[V_{NE 0}, V_{NE 1}, \dots, V_{NEp}]}^{T} \end{matrix}$ , 则由式(9)和式(10)可知, 线束导线近端串扰电压的均值 $\begin{matrix} {\bar{V}}_{NE} \end{matrix}$ =V_NE0, 标准差为 $\begin{matrix} σ_{V_{NE}} \end{matrix}$ = $\begin{matrix} \sqrt[]{\overset{m}{\sum_{i = 1}} V_{_{NEi}}^{2} < φ_{i}^{2} >} \end{matrix}$ 。于是线束导线近端串扰电压的变化范围可规定为 $\begin{matrix} [{\bar{V}}_{NE} - 3 σ_{V_{NE}}, {\bar{V}}_{NE} + 3 σ_{V_{NE}}] \end{matrix}$ , 此时在各种可能存在的线束导线几何布置的情况下, 其99.7%的串扰值将落于此区间范围内。

同时, 为了求取线束导线近端串扰电压的概率密度函数, 将线束导线近端串扰电压在频域进行混沌多项式展开得:

$\begin{matrix} |V_{NE}| = |\overset{m - 1}{\sum_{i = 0}} V_{NEi} φ_{i} (ξ)| \end{matrix}$ （24）

因此, 可通过数值方法对式(25)进行求解得到线束导线近端串扰电压的概率密度函数。

3 仿真验证

以如图1所示的线束为例, 利用PCE法对其串扰电压的统计特性进行分析预测。由2.3节可知, 模型输入为利用式(13)求得的符合标准正态分布的三维随机变量ξ = $\begin{matrix} {[ξ_{1}, ξ_{2}, ξ_{3}]}^{T} \end{matrix}$ , 当截断阶数p=1时, 由式(8)可得展开项数m=4, 混沌多项式展开的相关参数可通过表1和表2查询得到, 将式(14)和式(20)代入式(23)中, 整理可得:

$\begin{matrix} \{\begin{matrix} \tilde{V} = {[V_{0}, V_{1}, V_{2}, V_{3}]}^{T} \\ \tilde{I} = {[I_{0}, I_{1}, I_{2}, I_{3}]}^{T} \\ \tilde{C} = [\begin{matrix} C_{0} & C_{1} & C_{2} & C_{3} \\ C_{1} & C_{0} & 0 & 0 \\ C_{2} & 0 & C_{0} & 0 \\ C_{3} & 0 & 0 & C_{0} \end{matrix}] \\ \tilde{L} = [\begin{matrix} L_{0} & L_{1} & L_{2} & L_{3} \\ L_{1} & L_{0} & 0 & 0 \\ L_{2} & 0 & L_{0} & 0 \\ L_{3} & 0 & 0 & L_{0} \end{matrix}] \end{matrix} \end{matrix}$ （25）

式(19)所示的边界条件可改写为:

$\begin{matrix} \{\begin{matrix} \tilde{V} (0) = {\tilde{V}}_{S} - {\tilde{Z}}_{S} \tilde{I} (0) \\ \tilde{V} (l) = {\tilde{Z}}_{L} \tilde{I} (l) \end{matrix} \end{matrix}$ （26）

式中各项可表示为: $\begin{matrix} {\tilde{V}}_{S} \end{matrix}$ =[V_S, 0, 0, 0, 0, 0, 0, 0]^T, $\begin{matrix} {\tilde{Z}}_{S} \end{matrix}$ =diag([R_S, R_NE, R_S, R_NE, R_S, R_NE, R_S, R_NE]), $\begin{matrix} {\tilde{Z}}_{L} \end{matrix}$ =diag([R_L, R_FE, R_L, R_FE, R_L, R_FE, R_L, R_FE])。

接下来令Z_S和Z_L中的各阻抗值相等, 并分别考虑端接阻抗为高阻抗(R_S=R_L=R_NE=R_FE=1000 Ω )和低阻抗(R_S=R_L=R_NE=R_FE=50 Ω )两种情况下的线束导线近端串扰统计特征及其变化范围。

将式(25)和式(26)代入式(23), 经计算得到线束导线近端串扰电压在端接高阻抗和低阻抗两种情况下的统计特征, 并将其与N=3000次的蒙特卡洛法所得结果进行对比, 分别如图4和图5所示。

	Figure Option View Download New Window
	图4 端接高阻抗时PCE法与MC法频域近端串扰对比图Fig.4 Comparison of crosstalk in near end based on PCE and MC method in frequency domain while terminating high impedance

同时, 利用PCE法可计算得到V_NE_i, 因此采用数值方法通过式(24)能够求得各频率下线束导线在端接高阻抗和低阻抗情况下不同频率的近端串扰概率密度函数^[33]。并将其与3000次MC法的统计结果进行对比, 如图6所示。

	Figure Option View Download New Window
	图5 端接低阻抗时PCE法与MC法频域近端串扰对比图Fig.5 Comparison of crosstalk in near end based on PCE and MC method in frequency domain while terminating low impedance

	Figure Option View Download New Window
	图6 PCE法与MC法的频域近端串扰电压概率密度分布函数对比图Fig.6 Comparison of probability density function of crosstalk in near end based on PCE and MC method in frequency domain

由图4~图6可知, 在将决定线束导线几何位置的发射线对地高度、接收线对地高度, 以及发射线和接收线之间的距离这3个变量视为符合正态分布的随机变量时, 利用本文提出的PCE法计算获得的线束导线串扰统计特性(包括均值、标准差、概率密度函数及合理的变化范围)与3000次MC法的计算结果具有良好的一致性。

同时, 由表3可知, 在利用配置为i7-3770@3.40 GHz, 内存8 GB的个人计算机对线束导线串扰变化范围进行预测时, PCE法在保证计算结果准确可靠的前提下, 其计算效率要远远的高于MC法。

表3 线束导线串扰计算时间对比表(一阶PCE法与3000次MC法) Table 3 Comparison the computing time between Legendre PCE and MC method with 3000 samples

4 结束语

本文针对复杂系统线束导线几何位置非确定的情况, 提出了一种利用PCE法快速预测线束导线串扰统计特性的方法。通过与被广泛应用的MC法计算结果进行对比可知, PCE法不仅计算结果准确可靠, 同时其计算效率也要远远高于MC法。随着现代复杂系统中的线束种类和数量的不断增加, 在预测线束导线串扰方面, PCE法高效、准确等特点将对系统的电磁兼容设计有着重要的指导意义。同时, 本文对线束导线串扰统计特性的预测是基于线束导线位置变量符合正态分布进行的, 在接下来的工作中, 可以针对不同的分布类型(如均匀分布、Gamma分布和Beta分布等)对线束导线串扰统计特性进行更深入的研究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Paul Clayton R. 电磁兼容导论[M]. 闻映红, 译. 北京: 人民邮电出版社, 2007: 324. [本文引用:1]
[2]	Frei S, Jobava R G, Topchishvili D. Complex approaches for the calculation of EMC problems of large systems[C]//International Symposium on Electromagnetic Compatibility, Santa Clara, USA, 2004: 826-831. [本文引用:1]
[3]	Capraro G T, Paul C R. Design of the routing for EMC[C]//The 21st International Symposium on Electromagnetic Compatibility, 1979. [本文引用:1]
[4]	孙亚秀, 卓庆坤, 姜庆辉, 等. 基于多导体传输线理论的差模激励新型线束串扰模型研究[J]. 物理学报, 2015, 64(4): 1-13. Sun Ya-xiu, Zhuo Qing-kun, Jiang Qing-hui, et al. New differential-mode-source cable bundle crosstalk model based on multiconductor transmission lines theory[J]. Acta Phys Sin, 2015, 64(4): 1-13. [本文引用:1]
[5]	Ni G Y, Yan L, Yuan N C. Time-domain analytic solutions of two-wire transmission line excited by a plane-wave field[J]. Chinese Physics B, 2008, 17(10): 3629-3634. [本文引用:1]
[6]	Paul Clayton R. 多导体传输线分析[M]. 杨晓宪, 郑涛, 译. 北京: 中国电力出版社, 2013: 312-313. [本文引用:1]
[7]	吴振军, 王丽芳, 廖承林. 分析端接频变负载的多导体传输线FDTD新方法[J]. 物理学报, 2009, 58(9): 6146-6151. Wu Zhen-jun, Wang Li-fang, Liao Cheng-lin. A novel FDTD method for multi-conductor transmission lines terminating in frequency-dependent loads[J]. Acta Phys Sin, 2009, 58(9): 6146-6151. [本文引用:1]
[8]	Ferrieres X, Parmantier J P, Bertuol S, et al. Application of a hybrid finite difference/finite volume method to solve an automotive EMC problem[J]. IEEE Transactions on Electromagnetic Compatibility, 2004, 46(4): 624-634. [本文引用:1]
[9]	Zhang Q, Liou J J, Mcmacken J, et al. Development of robust interconnect model based on design of experiments and multiobjective optimization[J]. IEEE Transactions on Electron Devices, 2001, 48(9): 1885-1891. [本文引用:1]
[10]	Bellan D, Pignari S. A. probabilistic model for the response of an electrically short two-conductor transmission line driven by a rand om plane wave field[J]. IEEE Transactions on Electromagnetic Compatibility, 2001, 43(2): 130-139. [本文引用:1]
[11]	Shiran S, Reiser B, Cory H. A probabilistic method for the evaluation of coupling between transmission lines[J]. IEEE Transactions on Electromagnetic Compatibility, 1993, 35(3): 387-393. [本文引用:1]
[12]	Salio S, Canavero F, Lefebvre J, et al. Statistical description of signal propagation on rand om bundles of wires[C]//The 13th International Zurich Symposium Electromagnetic Compatibility, Zurich Switizerland , 1999: 499-504. [本文引用:1]
[13]	高印寒, 王天皓, 杨开宇, 等. 汽车线束的动态串扰特性预测[J]. 吉林大学学报: 工学版, 2014, 44(5): 1258-1263. Gao Yin-han, Wang Tian-hao, Yang Kai-yu, et al. Prediction of the dynamic crosstalk of automotive wiring hardness[J]. Journal of Jilin University (Engineering and Technology Edition) 2014, 44(5): 1258-1263. [本文引用:1]
[14]	Sun S, Liu G, Drewniak J L, et al. Hand -assembled cable bundle modeling for crosstalk and common-mode radiation prediction[J]. IEEE Transactions on Electromagnetic Compatibility, 2007, 49(3): 708-718. [本文引用:1]
[15]	Wu M, Beetner D, Hubing T, et al. Estimation of the statistical variation of crosstalk in wiring harnesses[C]//IEEE International Symposium on Electromagnetic Compatibility, Detroit, USA, 2008: 614-619. [本文引用:1]
[16]	Wu M, Beetner D G, Hubing T H, et al. Statistical prediction of "reasonable worst-case" crosstalk in cable bundles[J]. IEEE Transactions on Electromagnetic Compatibility, 2009, 51(3): 842-851. [本文引用:1]
[17]	Diouf F, Canavero F. Crosstalk statistics via collocation method[C]//IEEE International Symposium on Electromagnetic Compotibility, Austin, TX, USA, 2009: 92-97. [本文引用:1]
[18]	Salio S, Canavero F, Lecointe D, et al. Crosstalk prediction on wire bundles by Kriging approach[C]//IEEE International Symposium on Electromagnetic Compatibility, Washington DC, USA, 2000: 197-202. [本文引用:1]
[19]	Bellan D, Pignari S A, Spadacini G. Characterisation of crosstalk in terms of mean value and stand ard deviation multiconductor transmission lines[J]. IEE Proceedings on Science, Measurement and Technology, 2003, 150(6): 289-295. [本文引用:1]
[20]	Bellan D, Pignari S A, Spadacini G. Characterisation of crosstalk in terms of mean value and stand ard deviation multiconductor transmission lines[J]. IEE Proceedings on Science, Measurement and Technology, 2003, 150(6): 289-295. [本文引用:1]
[21]	Halligan M S, Beetner D G. Maximum crosstalk estimation in weakly coupled transmission lines[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(3): 736-744. [本文引用:1]
[22]	Wiener N. The homogeneous chaos[J]. American Journal of Mathematics, 1938, 60(1): 897-936. [本文引用:4]
[23]	Ghanem R G, Spanos P D. Stochastic Finite Elements: a Spectral Approach[M]. Berlin: Springer, 1991: 224. [本文引用:1]
[24]	Ghanem R. Ingredients for a general purpose stochastic finite elements implementation[J]. Computer Methods in Applied Mechanics & Engineering, 1999, 168(1-4): 19-34. [本文引用:1]
[25]	Finette S. A stochastic representation of environmental uncertainty and its coupling to acoustic wave propagation in ocean waveguides[J]. Acoustical Society of America Journal, 2006, 120(5): 2567. [本文引用:1]
[26]	Xiu D, Karniadakis G E. The wiener-askey polynomial chaos for stochastic differential equations[J]. SIAM Journal on Scientific Computing, 2002, 24(2): 619-644. [本文引用:1]
[27]	Xiu D, Karniadakis G E. A new stochastic approach to transient heat conduction modeling with uncertainty[J]. International Journal of Heat & Mass Transfer, 2003, 46(24): 4681-4693. [本文引用:1]
[28]	Stievano I S, Manfredi P, Canavero F G. Carbon nanotube interconnects: process variation via polynomial chaos[J]. IEEE Transactions on Electromagnetic Compatibility, 2012, 54(1): 140-148. [本文引用:1]
[29]	Cameron R H, Martin W T. The orthogonal development of non-linear functionals in series of fourier-hermite functionals[J]. Annals of Mathematics, 1947, 48(48): 385-392. [本文引用:1]
[30]	王晓东, 康顺. 多项式混沌方法在随机方腔流动模拟中的应用[J]. 中国科学: 技术科学, 2011, 33(6): 790-798. Wang Xiao-dong, Kang Shun. Application of polynomial chaos on numerical simulation of stochastic cavity flow[J]. Science China: Technological Sciences, 2011, 33(6): 790-798. [本文引用:1]
[31]	高印寒, 王瑞宝, 马玉刚, 等. 汽车线束导线间寄生电容及串扰的解析预测模型[J]. 吉林大学学报: 工学版, 2011, 41(增刊1): 144-149. Gao Yin-han, Wang Rui-bao, Ma Yu-gang, et al. Analytical prediction of parasitic capacitance and crosstalk in automotive cable bundles[J]. Journal of Jilin University (Engineering and Technology Edition) , 2011 , 41(Sup. 1) 144-149. [本文引用:1]
[32]	Paul C R. Decoupling the multiconductor transmission line equations[J]. IEEE Transactions on Microwave Theory & Techniques, 1996, 44(8): 1429-1440. [本文引用:1]
[33]	Papoulis A. Probability, Rand om Variables and Stochastic Processes[M]. 3rd ed. New York: McGraw-Hill, 1991: 207-209. [本文引用:1]

2007

0.0

... 但其也为干扰信号的传播提供了载体,不仅会提高临界设备及导线的噪声水平,还会对系统的传导发射和辐射发射产生影响,使得系统的整体电磁兼容性能剧烈下降^[1] ...

2004

0.0

... 因此,对于复杂系统的前期电磁兼容性设计,线束导线串扰是其预测的首要任务^[2] ...

1979

0.0

... 美国肯塔基大学的PAUL通过实验发现,串扰对线束导线的位置极为敏感,由于线束导线之间位置的变化,可导致串扰的变化高达20 dB^[3] ...

2015

0.0

. 2015, 64(4):1-13 DOI:doi:10.7498/aps.64.044102

New differential-mode-source cable bundle crosstalk model based on multiconductor transmission lines theory

基于多导体传输线理论的差模激励新型线束串扰模型研究

Sun Ya-xiu , Zhuo Qing-kun , Jiang Qing-hui

孙亚秀, 卓庆坤, 姜庆辉

The traditional cable bundle crosstalk model is established based on an intra-system common mode source, without considering the crosstalk of cable bundles stimulated by a differential-mode source between different systems. To solve the physical problem of crosstalk between independent circuit cable bundles which is stimulated by a differential-mode source, in this article we propose a new differential-mode source cable bundle crosstalk calculation method based on the multiconductor transmission line theory. According to the mechanism of the differential-mode-stimulated transmission line coupling, using this method we obtain a new three-conductor transmission line parasitic parameter circuit model and mathematic matrix model through using the transmission line propagating transverse electro magnetic mode. We deduce the parasitic parameter calculation formula by an image method and Neumann formula, and then obtain the new cable bundle crosstalk chain parameter array equations in frequency domain. By using the top and end boundary conditions of the new differential-mode cable bundle crosstalk model, we finally work out the crosstalk voltage in frequency domain. In this article, we take the crosstalk between differential-mode parallel double culprit cables and the victim cable from other independent circuit for example. By simulating the crosstalk voltage of victim cable in different position arrangements, we obtain the crosstalk physical law between cable bundles under the differential-mode source condition, that is, the crosstalk of the victim cable located between differential-mode circuits is much larger than that situated outside the differential-mode circuit. We can also verify that this model can be used to calculate the crosstalk caused by differential-mode source at different frequencies. In this article, we analytically calculate the crosstalk problems caused by differential-mode source cable bundles for the first time, which provides theoretical basis for solving some practical electromagnetic compatibility problems such as the bundling of a large quantity of wires and the predicting of cable bundle crosstalk. Therefore it perfects the application of multiconductor transmission line model to cable bundle crosstalk problem, and has strong guiding significance.

传统的线束串扰模型只是在系统内共模激励的基础上建立的, 没有考虑系统间差模激励下线束串扰的情况. 针对差模激励下系统独立回路间线束串扰的物理问题, 提出了一种基于多导体传输线理论的差模激励新型线束串扰的计算方法.该方法根据差模激励下线间的耦合机理, 利用传输线传播横向电磁模式得到新型三导体传输线寄生参数电路及数学矩阵模型, 通过镜像法以及诺埃曼公式推导出寄生参数的计算公式, 并在频域内得到新型线束串扰的链参数矩阵方程, 根据新型差模串扰模型始端、终端边界条件最终得到串扰电压的频域解.以差模激励下平行双线回路对其他回路受扰线的串扰为例, 通过仿真受扰线不同布置情况下的串扰电压, 得到了差模激励源的线束间串扰的物理规律, 即受扰线位于差模回路之间时所受的串扰要远大于位于回路外时所受的串扰, 并验证所提出的模型及方法可以计算不同频率差模激励引起的干扰. 利用解析的方法解决了线束串扰中差模激励下的导线串扰问题, 为实际中如大量导线的捆扎以及导线干扰的预测等电磁兼容问题提供了理论依据, 具有指导意义, 完善了多导体传输线理论在线束串扰中的应用.

... 但由于计算线束导线串扰的传统电磁学方法,如多导体传输线理论^[4,5],时域有限差分法^[6,7],矩量法^[8]等,都是针对线束导线位置固定的理想情况进行计算,对于非确定性几何布置的线束导线串扰计算,其不仅会消耗大量的计算资源,所获得的结果也并不理想 ...

2008

0.0

2013

0.0

2009

0.0

. 2009, 58(9):6146-6151

A novel FDTD method for multi-conductor transmission lines terminating in frequency-dependent loads

分析端接频变负载的多导体传输线FDTD新方法

Wu Zhen-jun , Wang Li-fang , Liao Cheng-lin.

吴振军, 王丽芳, 廖承林

A novel finite difference time domain （FDTD） method has been introduced to analyze multi-conductor transmission lines terminated with frequency-dependent loads. The admittance of frequency-dependent loads can be modeled by rational functions by using vector-fitting, then converting these functions into time-domain by inverse Fourier transform （IFT）. Based on the piecewise linear recursive convolution （PLRC） method, the relation between voltage and current of admittance parameters are deduced. Incorporating the formula into multiconductor transmission lines （MTL） FDTD equations, we get the general formula of MTL FDTD dealing with frequency-dependent loads. In simulating a typical circuit, the results agreed well with the results obtained by using the state-variable transmission model. It shows the method is valid in dealing with frequency-dependent loads.

提出了一种新的有效求解端接频变负载的时域有限差分法（FDTD）.该方法将频域导纳经矢量匹配后以有理式表示，通过逆傅里叶变换将其转换到时域，基于分段线性递归卷积法，推导出该导纳两端的电压和电流关系，将其代入到传输线FDTD模型中，得到了求解端接频变负载多导体（MTL）传输线FDTD的一般公式.对一典型电路进行了仿真，和以状态变量法求解任意负载的结果进行了对比，两者基本重合，说明该方法用来求解频变负载是有效的.

2004

0.0

2001

0.0

... 在目前已经开展的研究中,主要有蒙特卡洛(Monte Carlo,MC)法^[9,10,11]、分形图学法^[12,13,14]、卷积法^[15,16]、配置法^[17]、克里金法^[18],以及其他一些统计学方法^[19,20,21] ...

2001

0.0

1993

0.0

1999

0.0

2014

0.0

. 2014, 44(5):1258-1263 DOI:10.7964/jdxbgxb201405006

Prediction of the dynamic crosstalk of automotive wiring hardness

汽车线束的动态串扰特性预测

Gao Yin-han , Wang Tian-hao , Yang Kai-yu

高印寒, 王天皓, 杨开宇

1.State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,China; 2.College of Mechanical & Electrical Engineering,Jiangxi University of Science and Technology,Ganzhou 341000, China; 3.College of Instrumentation& Electrical Engineering,Jilin University,Changchun 130061,China

Different installation methods and different moving states of automobile can bring randomness to the relative position of wire in automobile wiring harness and ground height of wiring hardness. A statistic model is proposed to calculate the dynamic crosstalk of automobile wiring harness under the low frequency. The image method is employed to acquire the unit length distribution parameters of the wire with insulation layer, and the principle of statistics is applied to infer the mean value and variance of the dynamic crosstalk of wiring harness. The reasonable worst-case crosstalk value calculated by the proposed model is compared with the 273 times simulation results of random displacement spline interpolation to verify the accuracy and reliability of the model. The proposed statistic model can also adjust the relevant parameters flexibly according to practical situation and realize rapid prediction, which provide the basis to the design of vehicle electromagnetic compatibility. The model has very important practical significance.

针对汽车线束中导线相对位置和线束对地高度参数以及由于不同的安装方式和汽车不同的运动状态带来的随机性,提出了一种在低频下用来计算汽车线束动态串扰的统计学模型。利用镜像法计算获得了带有绝缘层导线的单位长度分布参数,运用统计学原理推导得到了线束动态串扰的均值与方差,并将计算所得合理的最差串扰值与273次随机中点布置样条插值法(RDSI)仿真结果进行了对比,验证了模型的准确性和可靠性。所建立的线束动态串扰统计模型可以根据实际情况灵活调整相关参数,实现快速预测,为车辆电磁兼容性设计提供依据。

2007

0.0

2008

0.0

2009

0.0

2009

0.0

2000

0.0

2003

0.0

2003

0.0

2014

0.0

1938

0.0

... 1 混沌多项式展开法的数学模型混沌多项式展开法来源于Wiener^[22]所提出的同性混沌法,它是一种严密高效的不确定分析方法,具有很强的数学支撑 ...

... Wiener^[22]最初利用PCE法提出并建立了湍流计算模型 ...

... Wiener采用与高斯型随机变量对应的Hermite正交多项式为基函数对随机过程谱展开^[22] ...

... 针对高斯随机过程,Wiener^[22]确定了以Hermite正交多项式为基函数进行混沌多项式展开的表达式: ...

1991

0.0

... 随后许多学者将该理论推广至其它工程领域,如结构力学领域^[23,24],环境与声场领域^[25],随机差分方程领域^[26],瞬态热传导领域^[27],以及纳米材料电特性领域^[28]等方面 ...

1999

0.0

2006

0.0

2002

0.0

2003

0.0

2012

0.0

1947

0.0

... 其中Cameron-Martini定理证明了该展开能够以正交多项式的形式对任意随机过程进行描述^[29] ...

2011

0.0

. 2011, 33(6):790-798

Application of polynomial chaos on numerical simulation of stochastic cavity flow

多项式混沌方法在随机方腔流动模拟中的应用

Wang Xiao-dong , Kang Shun.

王晓东, 康顺

... 利用式(7)和式(8)可分别得到原始模型混沌多项式展开后的展开系数和展开项数,根据Hermite正交多项式所具有的正交性,原始模型对输入随机变量的响应均值Y_mean为^[30]: ...

2011

0.0

. 2011, 41(增刊1):144-149

Analytical prediction of parasitic capacitance and crosstalk in automotive cable bundles

汽车线束导线间寄生电容及串扰的解析预测模型

Gao Yin-han , Wang Rui-bao , Ma Yu-gang

高印寒, 王瑞宝, 马玉刚

The space full of inhomogeneous media was turned into the infinite space full of homogeneous media using the method of image,and the relation between the bound charges and the free charges on the conductors inside the homogeneous media on the basis of the theory of electromagnetic field,then the analytical model of the per unit length parasitic parameter of insulated conductors in cable bundles was derived and the relevant crosstalk was also estimated.The results of p.u.l parasitic parameter and the crosstalk from the analytical model compared the results from the EMC Studio software.It was turn out that the analytical model was valid.The analytical model was simple,convenient and it can provide a rapid prediction about parasitic parameter and crosstalk of conductor ensure the problem will not be missed especially in the early stage of design absence of complete system information.The analytical model was fit for deterministic and stochastic harness geometry.

应用镜像法把非均匀介质空间变换成无限大均匀介质空间,依靠电磁场理论得到非均匀介质导线束缚电荷与自由电荷的关系,推导出汽车线束内有绝缘层的非均匀介质导线单位长度寄生电容解析模型,并计算相应串扰。以某汽车线束为例,分别用推导的解析公式和EMC Studio软件对线束单位长度寄生电容和串扰进行了计算比较,验证了解析公式的正确性。本文解析模型方便、简单,能够在缺少完整信息的初期设计阶段,快速预测寄生电容和串扰,适用于汽车静态时线束内导线确定性几何布置和动态时的随机性几何布置。

1996

0.0

... 由上述已知条件,利用模式理论^[32]可分别求得近端串扰电压V_NE和远端串扰电压V_FE等参数 ...

1991

0.0

... 同时,利用PCE法可计算得到V_NE_i,因此采用数值方法通过式(24)能够求得各频率下线束导线在端接高阻抗和低阻抗情况下不同频率的近端串扰概率密度函数^[33] ...