边缘检测的实质是利用某种策略来提取图像中前景和背景的边界线。边缘即为图像中灰度发生剧烈变化的区域边界。图像灰度变化的梯度反映了图像灰度的变化程度, 因此经常利用图像中各像素的小范围邻域来构造边缘检测算子。常用的边缘检测算子有Sobel算子^[1], Prewitt算子^[2], Laplacian算子^[3], Canny算子^[4]。近年来, 涌现了许多新兴的算法如:基于小波变换的边缘检测算法^[5], 基于模糊理论的边缘检测方法^[6], 基于聚类的边缘检测方法^[7], 基于群体智能的边缘检测算法。

群体智能作为人工智能的一个分支, 利用了自组织分散算法提供了动态、自组织、灵活的解决方案。因为群体智能在其大部分过程中保有随机性, 它在众多领域都提供了具有鲁棒性的解决方案, 近几年针对科学研究和工程问题, 群体智能的应用有大幅增长。

本文所使用蚁群算法作为群体智能中的经典算法之一, 最早由Dorigo^[8]提出, 运用正反馈的原理和蚂蚁间分布式合作来找到最优解。作为以种群为基础寻求更佳路线的方法, 蚂蚁个体间的信息交换尤其重要, 寻找出洞穴到食物的最佳路线。由于蚁群算法的这个特性, 2005年, Bao等^[9]将其应用到边缘检测中, 取得了不错的成果。2013年, Mullen等^[10]提出了一种自适应变化的阈值策略, 利用每只蚂蚁的局部阈值代替全局阈值, 而且每只蚂蚁个体的局部阈值在其移动过程中都将发生动态变化, 优化了边缘检测的结果。2015年, Liu等^[11]采用一种新的启发式函数, 并利用用户定义阈值的信息素更新过程, 提供一组合适的参数值进一步提高了检测精度。2016年, Dorrani等^[12]在Liu的基础上对含噪声的图像实验同样取得了良好的效果, 同年, Che等^[13]提出了将Otsu算法作为蚁群算法的初始化流程。

本文利用Otsu预处理, 在信息素矩阵和启发式矩阵初始化做了改进, 同时加入信息素异步更新策略和参数自适应修改来避免过早陷入停滞从而发现更多弱边缘。本文方法提取了更多的连续边缘以及弱边缘, 具有更好的鲁棒性。

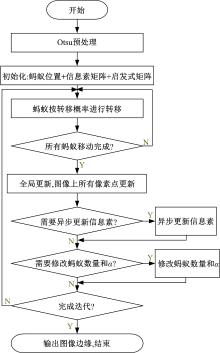
本文基于文献[13]的研究成果加以改进, 成功地发现了更多的连续边缘以及弱边缘。蚁群算法的基本过程如下:

设N只蚂蚁被初始随机分配在若干不同的N个像素点上, 每个蚂蚁个体都有一个移动的准则, 遵循:

(1)由像素i到下一允许访问的像素点j由启发式信息及边上的信息素同时控制选取哪一像素点, 可以用函数表达。

(2)为强行制约蚁群合理地移动, 规定每个个体不能经过刚访问的像素点, 由tabu表控制。

(3)每当做完周游后, 蚂蚁个体能于经过的边残留下信息素。

令τ _ij(t)为像素点i与像素点j之间的信息素大小。在每次发生蚂蚁移动后, 信息素发生变化, 由于信息素有一个蒸发率, 所以有如下信息素更新准则:

τijt+n=1-ρτijt+Δτij1

式中:ρ 为从这次周游后信息素消散水平。

Δτij=∑k=1nΔτijk（2）

Δτijk=ηij/255, 第k只蚂蚁在(i, j)且ηij> T0, 其他（3）

式中:Δ τijk为第k个蚂蚁个体一次移动完成时留存于像素i与像素j连接边上信息素大小; T为用户定义的一个阈值, 只允许启发式信息大于一个特定的常数值的蚂蚁释放信息素; η 为在每一时间点每只蚂蚁的可见性, 即每只蚂蚁从当前像素转移到周围8像素的能见性, 比如在像素(x, y)处:

η _{x-1, y-1}=I(x-1, y)-I(x, y-1)

η _{x-1, y}=I(x-1, y-1)-I(x-1, y+1)

η _{x-1, y+1}=I(x-1, y)-I(x, y+1)

η _{x, y-1}=I(x+1, y-1)-I(x-1, y-1)

η _{x, y+1}=I(x-1, y+1)-I(x+1, y+1)

η _{x+1, y-1}=I(x, y-1)-I(x+1, y)

η _{x+1, y}=I(x+1, y-1)-I(x+1, y+1)

η _{x+1, y+1}=I(x+1, y)-I(x, y+1)

以上各项均为取绝对值后的结果。

定义从像素i转到像素j在时刻t转移概率为:

pijk(t)=[τij(t)]α[ηij(t)]βΣs[τij(t)]α[ηij(t)]β, if(i, j)∈allok0, else（4）

式中:allo_k为第k只蚂蚁的周围8个像素点, 已走过的任意像素即tabu表中的像素点除外; α 和β 分别控制相对信息素路径和可见性的相对重要性, 转移几率是灰度梯度(梯度大的被选几率高, 贪婪性试探法)和信息素浓度共同作用的结果。

很显然, 阈值T是直接影响信息素路径的关键, 进而影响了算法的效果, 当T值很小时, 蚂蚁将释放大量信息素, 其中包括了很多的弱边缘, 而且提取许多背景信息或噪声信息, 不利于提取。当T值很大时, 只允许蚂蚁释放少量信息素, 导致了蚂蚁只能搜索到强边缘而忽略弱边缘, 并且出现许多不连续的边缘线。所以, 取合适的T值显得尤为重要。

文献[13]提出了一种T自适应的阈值改进措施, 代替一个用户自定义的全局阈值, T的更新策略如下:

T(t)n=T(t-1)n+1, ifηn(x, y)> T(t-1)nT(t-1)n-1, ifηn(x, y)< T(t-1)nT-, ifT(t-1)n< T-（5）

式中: T-为每次迭代之后所有蚂蚁的平均阈值; η _n(x, y)为第n只蚂蚁个体在(x, y)像素点处的能见度。

实验流程图如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 流程图Fig.1 Flow chart

由于蚁群算法处理的问题都是NP完全问题, 不存在最优解, 以下初始参数选取均是实验中取得最好效果的值。

蚂蚁数量K:由于蚁群算法是群智能算法, 依赖群体之间的协作和信息传递, 蚂蚁数量越多取得效果越好, 本文设置为 MN。

信息素蒸发率因子ρ :ρ 影响到整个方法收敛速度与功能。ρ 越大, 增长越快, ρ =1时, 只需一次就到达了最大阈值; ρ 越小, 收敛速度越快, 本文将其设置为0.1。

启发式因子β :β 是启发式信息在搜寻时指示个体选取最优行动轨迹的影响力, 若β 太小, 便变为纯正的任意搜寻方法, 找寻到最佳方案的可能性非常低; 若β 太大, 所搜寻到的最佳方案将会有越来越差的趋向。本文将其设置成2。

初始信息素大小:由文献[11]给出, 本实验将其设置为0.0001。

用户自定义初始阈值T:由文献[13]给出, 本实验将其设置为35。

最大迭代次数:迭代次数越大, 蚂蚁可以寻到越多路径(边缘), 由文献[13]给出, 本实验将其设置为300。

其他参数如下:信息素相对影响力因子α 变化后分别为2, 1, 0.5; λ 为1; 异步更新时的迭代次数为50; 信息素相对影响因子修改时的迭代次数为100。

3.1 主观对比

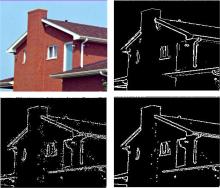
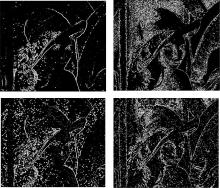
图2~图5分别为基于Lena图像以及从USC-SIPI数据集中的Peppers, House, Cameraman图像在Matlab实验环境下所得到的结果, 图中从左上至右下依次为原图, 文献[11]方法, 文献[13]方法和本文方法结果。

对比每幅图的左下和右下图像可以看出, 本文方法在文献[11]和文献[13]的基础上效果有很大的改进, 能更精确、更多地发现弱边缘, 而且, 本文方法也减少了图像中背景被归为边缘的错误, 在查准率和查全率方面都有明显提高。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 Lena图像及结果Fig.2 Lena pictures and results

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Peppers图像及结果Fig.3 Peppers pictures and results

对于有噪声的图像, 本文同样发现了了更多的弱边缘。

图6中的左图和右图分别是Lena图像加入0.02的高斯噪声和椒盐噪声使用文献[12]方法以及本文方法处理得到的结果。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 House图像及结果Fig.4 House pictures and results

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 Cameraman图像及结果Fig.5 Cameraman pictures and results

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 含噪声的Lena图像处理结果Fig.6 Results of Lena pictures with noise

3.2 定量分析

本文使用的是BSDS300数据库, 该数据库包含了彩色、灰度以及标注过的真实数据, 即边缘二值图像。基于如下指标进行评价:TP, 预测为边缘, 实际也是边缘的像素数; FP, 预测为边缘, 实际不是边缘的像素数; TN, 预测不是边缘, 实际不是边缘的像素数; FN, 预测不是边缘, 实际是边缘的像素数; TPR=TP/(TP+FN), 实际是边缘的像素被成功提取的百分比; FPR=FP/(FP+TN), 实际不是边缘的像素被错误提取为边缘像素的百分比。表1为实验结果对比。

表1

Table 1

表1(Table 1)

表1 实验结果对比 Table 1 Experimental results comparison 图像 方法 TPR FPR Kaola 文献[11] 0.47 0.16 文献[13] 0.69 0.24 本文 0.80 0.30 Plane 文献[11] 0.67 0.18 文献[13] 0.58 0.25 本文 0.72 0.24 House 文献[11] 0.82 0.13 文献[13] 0.68 0.12 本文 0.84 0.13

表1 实验结果对比 Table 1 Experimental results comparison

图7、图8、图9中从左上至右下依次是原图, 文献[11]方法, 文献[13]方法以及本文方法处理得到的结果。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 Kaola图像及结果Fig.7 Kaola pictures and results

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 Plane图像及结果Fig.8 Plane pictures and results

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 House图像及结果Fig.9 House pictures and results

针对蚁群算法检测检测边缘时出现的边缘不连续以及算法易陷入停滞的问题, 提出了改进的方法, 有效地提取了更多的弱边缘和连续的边缘, 在有噪声的图像中能够得到较好的结果, 在对自然图像提取边缘方面具有鲁棒性和精确性。本文对于自然图像的实验取得了较好的结果, 但是对于特定领域的图像如医学图像, 因为其存在一些特定的病理情况或其他特殊原因, 结构边缘十分模糊, 所以很难被准确检测。对于这类图像, 蚁群算法在提取边缘过程中往往不能提取到较细的边缘特征, 以至于不能得到较精确的检测结果。