基于二部图模型的欠、过约束几何约束系统的识别和处理

引用本文

李文辉, 孙明玉, 许光星, 曹春红. 基于二部图模型的欠、过约束几何约束系统的识别和处理. 吉林大学学报（工学版）, 2017, 47(5): 1583-1590
LI Wen-hui, SUN Ming-yu, XU Guang-xing, CAO Chun-hong. Identification and process of under- and over-constrained geometric constraint systems based on bipartite graph model. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1583-1590 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705034
Permissions

基于二部图模型的欠、过约束几何约束系统的识别和处理

李文辉¹, 孙明玉¹, 许光星², 曹春红²

1.吉林大学计算机科学与技术学院,长春 130012

2.东北大学计算机科学与工程学院,沈阳 110819

作者简介:李文辉(1961-),男,教授,博士生导师.研究方向:计算机辅助设计,计算机图形学.E-mail:liwenhui2050@163.com

基金项目:国家自然科学基金项目(61300096); 吉林省科技厅发展计划项目(20140101181JC)

摘要

采用表达几何基元参数和基本几何约束的二部图模型表示几何约束系统,提出一种新的基于二部图最大匹配的几何约束求解方法,并由二部图分解法对几何约束系统的欠、过约束属性进行识别。通过加入几何约束优先级,改进几何约束装配机制来处理欠约束几何约束系统;当处理过约束的几何约束系统时,由改进的人工蜂群算法识别一致性与非一致性过约束并对识别的过约束子域进行有效处理。研究结果表明,本文基于新的二部图模型的几何约束求解方法是行之有效的。

关键词: 计算机应用; 几何约束求解; 二部图分解; 欠约束子域; 过约束子域

中图分类号:TP391.7 文献标志码:A 文章编号:1671-5497(2017)05-1583-08

Identification and process of under- and over-constrained geometric constraint systems based on bipartite graph model

LI Wen-hui¹, SUN Ming-yu¹, XU Guang-xing², CAO Chun-hong²

1.College of Computer Science and Technology, Jilin University, Changchun 130012, China

2. College of Computer Science and Engineering, Northeastern University, Shenyang 110819, China

Abstract

In this paper, a geometric constraint system is represented by a bipartite graph model, which expresses geometric primitive parameters and basic geometric constraints, and a new Geometric Constraint Solving (GCS) method based on the maximum matching of bipartite graph is proposed. The under- and over-constrained sub-domains are identified by using the bipartite graph decomposition method. An under-constrained sub-domain is processed by introducing the geometric constraint priority and improving the geometric constraint assembly mechanism. The consistent and inconsistent over-constraints are identified by the modified artificial bee colony algorithm, and the identified over-constrained sub-domain is also effectively processed. Research results show that the GCS method based on the new bipartite graph model is effective.

Key words: computer application; geometric constraint solving; bipartite graph decomposition; under-constrained sub-domain; over-constrained sub-domain

Show Figures

0 引言

几何约束求解^[1](Geometric constraint solving, GCS)可理解为几何造型(如:产品模型、分子结构造型、工程设计用图等)设计的自动化, 即给定造型的几何约束关系后, 自动生成用户所需设计造型的过程。它作为现代参数化、变量化设计体系的核心, 是现代化计算机辅助设计(Computer aided design, CAD)和计算机辅助制造(Computer aided manufacture, CAM)的重要标志之一^{[2, 3]}。几何约束求解也被广泛应用于产品造型、装配设计、虚拟现实、运动学分析、化学分子建模、机器人动力学和教学几何等诸多领域。

目前, 几何约束求解方法主要包括:数值计算法^{[4, 5, 6]}、符号代数法^[7]、基于规则的方法^[8]和基于图论的方法^[9]。其中, 基于图论的几何约束求解方法以其求解效率高、求解性能稳定在其他各几何约束求解方法中已占据主导地位。该方法使用图来表达一个几何约束系统, 采用一种“ 分而治之” 的策略, 首先, 将系统分解为一系列独立可解的子约束域; 其次; 对分解后获得的子域采用代数或几何的方法进行求解; 最后, 对子域的解进行合并, 获得原几何约束系统的最终解。

本文在使用二部图模型表达几何约束系统的基础上, 提出一种新的基于二部图最大匹配的几何约束求解方法, 该方法由二部图分解机制正确识别一个几何约束系统包含的欠约束和过约束子域, 并通过添加几何约束优先级和改进几何约束装配机制的策略处理欠约束子域, 通过文献[10]中改进的人工蜂群(ABC)算法识别出过约束子域内的一致性与非一致性过约束, 不同类型的过约束问题采用不同的处理方法。

1 几何约束系统冗余性判定

1.1 几何约束系统的建模

对几何约束系统建模是分析系统冗余和几何约束求解的重要前提。本文采用二部图模型对一个几何约束系统实施建模。二部图^[11]是图论中一种特殊的图表达方式, 其主要特点是:图的顶点集被划分为两个不相交的子集, 每条边所关联的两顶点分别属于这两个子集。由二部图模型表示的几何约束系统中, 一个子集表示几何基元, 另一个子集表示几何约束, 边集则表示几何基元与几何约束相关联。该二部图模型完全建立在几何基元与几何约束的相关性上, 因此, 识别系统约束属性(良、欠和过约束)也完全是根据几何基元自由度和几何约束的约束度二者间的这种相关性进行, 导致约束属性的识别仅是建立在结构意义上而绝非几何意义上, 使二者不完全等价, 而本文旨在有效识别出几何约束系统在几何意义上的欠和过约束属性。因此, 针对传统二部图建模方法存在的缺陷进行改进, 新二部图建模方法建立在几何基元参数和基本几何约束的关系上, 用以准确描述几何基元参数和基本几何约束的关系。

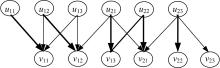
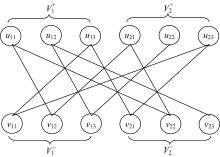假设存在几何约束系统GS=(O, C), 其中O={g_i|1≤ i≤ m}为m个几何基元, C={c_j|1≤ j≤ n}为n个几何约束。假设G=(V⁺, V^-, E)为二部图, 其中V⁺={ $\begin{matrix} V_{i}^{+} \end{matrix}$ |1≤ i≤ m}表示几何基元集O, 其元素 $\begin{matrix} V_{i}^{+} \end{matrix}$ ={u_ip|1≤ p≤ k}, k为g_i的自由度, u_ip为g_i的第p个参数; V^-={ $\begin{matrix} V_{j}^{-} \end{matrix}$ |1≤ j≤ n}为几何约束集C, 其元素 $\begin{matrix} V_{j}^{-} \end{matrix}$ ={v_jq|1≤ q≤ l}, l为c_j的约束度, v_jq表示c_j经过分解后的第q个基本几何约束。当g_i的第p个参数u_ip与c_j的第q个基本几何约束v_jq相关联时, 则在对应的二部图模型中由一条边E_ip_,_jq关联u_ip与v_jq。在V^-中装配用于固定造型的R个基本几何约束v_b₁~v_bR, 并将其与相关联几何基元的参数相连接, 它们可以对任意几何基元施加约束。R在二维和三维情况下的取值分别为3和6。

	Figure Option View Download New Window
	图1 基于新二部图模型的几何约束系统表示实例Fig.1 Example of geometric constraint system representation based on the new bipartite graph model

图1为基于本文二部图模型所表示的几何约束系统实例。其中, u_ij(1≤ i≤ 2, 1≤ j≤ 3)为几何基元 $\begin{matrix} V_{i}^{+} \end{matrix}$ 的第j个参数; v_ij(1≤ i≤ 2, 1≤ j≤ 3)为几何约束 $\begin{matrix} V_{i}^{-} \end{matrix}$ 经分解后所获得的第j个基本几何约束; 而边则表明对应的几何基元与几何约束相关, 如边(u₁₂, v₁₃)表示u₁₂与v₁₃相关。

提出的新的几何约束系统建模方法能够将几何基元和基本几何约束的具体参数相关联, 进一步精确描述约束关系。假设分解获得的基本约束的约束度为1, 任何复杂几何约束均可由分解后的基本几何约束来表示。

1.2 二部图最大匹配

二部图最大匹配的目的是:由适合方法使二部图顶点的可匹配对的数量达到最大。二部图最大匹配的方法众多, 典型的有:①枚举方法, 该方法的时间复杂度过大, 通常不适用于规模较大的二部图模型。②最小点覆盖方法, 该方法虽能获得最大匹配, 但时间复杂度仍然过大, 为NP难问题。③网络流量算法, 该算法实现较为复杂, 难于理解。④匈牙利算法, 是对网络流算法的简化, 但时间复杂度也较大, 难于理解。本文提出基于结点度优先级的最优选择算法, 时间复杂度为O(mn)。

二部图的最大匹配可以简化, 从另一角度, 若假设:当前无匹配对可再进行匹配, 但匹配不是最大的, 则必然存在某个不是最优的匹配, 它使某一顶点失去了选择最佳匹配的机会。因此, 在最大匹配过程中应保证每一匹配对均为最优。本算法的目的是花费最小代价以获得数量最多的匹配对, 换言之, 使用最少的选择权获得二部图的最大匹配。

根据上述分析, 为有效保证二部图模型的最大匹配, 可使度越小的顶点具有越高的优先级, 使匹配选择均为最优。假设二部图为G=(V⁺, V^-, E), 该匹配算法如下:

算法1 基于顶点度的几何约束系统的二部图最大匹配。

步骤1 遍历V⁺(或者V^-)包含的顶点, 如果V⁺不为空集, 找到V⁺中所包含的优先级最高的顶点u, 否则, 算法终止。

步骤2 通过遍历关联u的顶点找到优先级最高的顶点v。

步骤3 装配一条边(u, v)到最大匹配集M。

步骤4 分别拆卸V⁺、V^-的顶点u、v和E的边(u, v)。

步骤5 拆卸该二部图G中所有度等于0的顶点, 转步骤1。

记D(u)为顶点u的度。由算法1构造的集合M为二部图G的一个最大匹配。

定理1 由算法1所获得的每一匹配都是当前最优选择。

证明:令u、v分别为V⁺和V⁺中包含的优先级最高的顶点。

(1)当D(u)=D(v)=1, 此时, 二者仅彼此相互连接。那么, 显然u、v为最佳匹配。

(2)当D(u)=1, D(v)> 1, 同时存在u'∈ V⁺满足:D(u')=1, u'与v相连接。那么, u和u'具有相同的优先级, 其中任一顶点与v相匹配时, 另一顶点将成为孤立点。此时, 将u和v相匹配, 拆卸u'。

(3)当D(u)> 1, D(v)=1, 同时存在v'∈ V^-满足:D(v')=1, v'与u相连接。与(2)中情况相类似, 针对顶点u, v和v'的优先级相同。此时, u与v相匹配, 拆卸v'。

(4)当D(u)> 1, D(v)> 1, 由于顶点u在V⁺中的优先级最高, 所以u将作为对V^-中影响最小的匹配对象。类似地, v将作为对V⁺中影响最小的匹配对象。同时, 由于D(u)> 1, 则与v相连接的顶点的度必然大于1, 同样, 与u相连接的顶点的度也必然大于1, 而在二者相匹配和拆卸关联它们的边后, 与u和v相连接的顶点的度均减少1, 但这些顶点的度仍大于1, 因此仍然具有匹配机会, 则u与v的匹配是当前最佳的。

由算法1 能够找到图1中二部图模型G的一个最大匹配, 如图2中的粗线部分所示, 最大匹配为M={(u₁₁, v₁₁), (u₁₂, v₁₂), (u₂₁, v₁₃), (u₂₂, v₂₁), (u₂₃, v₂₂)}。根据遍历顺序的不同, 被选择的优先级相同的顶点不同, 因此获取的最大匹配并非唯一。

	Figure Option View Download New Window
	图2 二部图的最大匹配表示Fig.2 The maximum matching representation of bipartite graph

1.3 基于二部图的识别算法

针对几何约束系统约束属性的识别, 可使用DM分解法^[12]将二部图模型分解为由子图构成的集合, 集合中的每一子图也均为二部图。由分析识别出这些子图的约束属性, 并根据偏序关系推导出系统的求解序列。

仍然假设GS=(O, C)为一个几何约束系统, G=(V⁺, V^-, E)为二部图模型, G₀, G₁, G₂, …, G_r, $\begin{matrix} G_{\infty} \end{matrix}$ 为使用DM分解法分解G后的子图序列。记DOF(g)为几何基元g的自由度, DOC(c)为几何约束c的约束度, 则DOF(G)=∑ _iDOF(g_i)-∑ _jDOF(c_j)。

定理2 在DM分解法的生成序列G₀, G₁, G₂, …, G_r, $\begin{matrix} G_{\infty} \end{matrix}$ 中, G₁, G₂, …, G_r为良约束子域, G₀和 $\begin{matrix} G_{\infty} \end{matrix}$ 分别为欠约束和过约束子域。

证明:G₀, G₁, G₂, …, G_r为DM分解的强联通子图, 其任一子图G_i中几何基元的自由度与几何约束的约束度相等, 几何基元参数与几何约束一一对应使G_i的几何约束方程组中约束方程的数量与求解变量的数量相等。因此, 约束方程组满秩, 存在唯一解, 由提出的二部图建模方法得到G₁, G₂, …, G_r为良约束子域。

根据几何约束系统欠约束的定义, 若子图G₀满足DOF(G₀)> 0, 则G₀为欠约束子图。根据DM分解法, G₀=S⁺∪ {u|u∈ V⁺∪ V^-, v∈ S⁺, v→ u}, 其中S⁺⊂V⁺为非饱和顶点集, 且若存在饱和顶点v∈ G₀∩ V^-, 则必然存在顶点u∈ V⁺满足u是饱和顶点, v→ u, 进一步地v∈ G₀。G₀中分别属于V⁺和V^-的饱和顶点数相等, 则有 $\begin{matrix} |G_{0} ⋂ V^{+}| \end{matrix}$ - $\begin{matrix} |G_{0} ⋂ V^{-}| \end{matrix}$ = $\begin{matrix} |S^{+}| \end{matrix}$ 成立, 而S⁺≠ φ , 得出DOF(G₀)> 0。因此, G₀为G的欠约束子域。类似地, $\begin{matrix} G_{\infty} \end{matrix}$ 为G的欠约束子域。

2 冗余处理

本文通过改进几何约束装配机制处理欠约束的几何约束系统提高算法效率, 并针对传统符号算法实现复杂、计算量大和求解效率低等不足, 采用文献[10]中改进的ABC算法识别过约束子域的一致性与非一致性。

由几何约束系统的偏序关系可以知道, 若系统同时包含欠约束和过约束子域, 它的过约束子域应优先予以处理; 其次为良约束子域; 最后为欠约束子域。按照这一顺序处理子域的优点是:针对欠约束子域的处理, 可由草图判断所装配的几何约束是否与设计者的设计意图保持一致。

2.1 欠约束子域的处理

几何约束系统欠约束的本质是对几何造型在形态或位置上限制不足导致其产生形变或位移, 反映在几何约束方程组上是指待解未知量在数量上大于方程的数量, 使约束方程组包含无限数量的解。因此, 需要在几何约束系统中装配几何约束使之转换为良约束的几何约束系统。转换的核心思想是:首先, 分解该子域为元素互不相关的集合, 该集合的每一元素仍为欠约束子域; 其次, 由优先级选择性地装配满足条件的几何约束或几何约束组合; 最后, 对所装配几何约束的有效性进行判断。

由于几何约束系统出现欠约束的位置可能不是唯一的, 因此, 分解是针对G₀在整体进行, 所有欠约束子域的顶点均包含于V₀。此时, V₀被分解为r个相互独立的子集V₀₁, V₀₂, …, V₀_r, 其中任意一个V₀_i(1≤ i≤ r)为独立且不可分解的欠约束子域的顶点集, V₀_i∩ V₀_j=φ , 1≤ i, j≤ r。按顺序对V₀_i进行处理。

添加几何约束优先级时, 由于顶点集V₀中仅有其饱和性质受最大匹配影响, 所以装配几何约束时, V₀中所有顶点的优先级相同, 且除V₀外的几何基元间的几何约束或几何约束组合与V₀不相关, 对V₀的欠、过约束属性无任何影响, 导致装配失效。这里, 针对欠约束子域的处理设置3个装配几何约束的优先级:

(1)V₀_i中几何基元间的几何约束或几何约束组合。

(2)V₀_i中与V₀_i以外的几何基元间的几何约束或几何约束组合。

(3)V₀_i中与V₀_j几何基元间的几何约束或几何约束组合。

若优先级相同, 优先选择一元几何约束, 其次是二元、三元, 以此类推, 且优先选择拓扑几何约束。需要注意:装配几何约束或几何约束组合时应避免使用同类型几何约束, 包括距离和角度。换言之, 在几何基元内部或几何基元间装配时, 需对同类型几何约束是否已经存在做出准确判断, 若存在, 则装配无效, 继续选取另一个满足条件的几何约束或几何约束组合进行装配。

对于装配是否有效, 仍然使用DM分解法判断新生成的二部图是否为最大匹配, 若是, 则装配有效。由于V₀外的二部图是良约束子域, 且与它所包含的几何约束不相关, 所以, 判断只需对装配了几何约束或几何约束组合的V₀进行即可。当装配的几何约束对设计者未知, 则装配仍然无效。若判断出所装配的几何约束有效, 则由求解序列求解几何约束系统, 生成满足约束的几何造型。若生成的几何造型与设计意图不相符, 表明装配了不正确的几何约束, 需重新选择进行装配。

算法2 欠约束子域的处理

步骤1 分解欠约束子域的顶点集V₀为r个不相关的子欠约束域顶点集{V₀_i|1≤ i≤ r}, 其中V₀_i∩ V₀_j=φ , 1≤ i, j≤ r。

步骤2 按照V₀_i的生成顺序计算所有V₀_i的子约束域的自由度DOF(G₀_i), 记为k。

步骤3 按照装配优先级, 搜索几何基元内部或几何基元之间满足DOC(c)=k的几何约束c或满足∑ _jDOF(c_j)=k的几何约束组合∪ _jc_j。

步骤4 分解搜索到的满足DOC(c)> 1的几何约束或者满足∑ _jDOF(c_j)> 1的几何约束组合为基本几何约束的组合, 并判断与其相关联的几何基元内部或几何基元间参数是否已经存在同类型的几何约束, 若存在, 表明该基本几何约束无效, 转步骤3。

步骤5 添加搜索到的几何约束或几何约束组合到V₀_i, 并由DM分解法判断装配几何约束后的子图是否为最大匹配, 若不是, 设置装配部分中包含于过约束子域的基本几何约束为无效, 转步骤3。

步骤6 若所装配的几何约束对设计者而言不可知, 则设置该约束为无效, 转步骤3; 否则, 按照求解序列求解几何约束系统, 生成满足约束的几何造型, 若造型与设计意图不相符, 则将装配的几何约束中不相符约束设为无效, 转步骤3。

步骤7 若i≠ r, i=i+1, 转步骤2; 否则, 算法终止。

2.2 过约束子域的处理

几何约束系统过约束是指在形态和位置上对造型限制过多, 换言之, 几何约束方程组中待解变量的数量大于方程数量, 导致方程组可能无解。因此, 需要通过拆卸多余的几何约束, 使系统转换为良约束的几何约束系统。

针对过约束子域的处理, 首先, 分解该子域为不相关的过约束域的集合; 其次, 对集合中每一元素的过约束类型做出有效判断; 最后, 根据不同的过约束类型选择适合的处理方法。

同样地, 由于过约束存在于几何约束系统的位置并非唯一, 所以仍然在整体上分解子图 $\begin{matrix} G_{\infty} \end{matrix}$ , 该子图包含过约束子域顶点集 $\begin{matrix} V_{\infty} \end{matrix}$ 。分解 $\begin{matrix} V_{\infty} \end{matrix}$ 获得r个相互独立的子集 $\begin{matrix} V_{\infty 1} \end{matrix}$ , $\begin{matrix} V_{\infty 2} \end{matrix}$ , …, $\begin{matrix} V_{\infty r} \end{matrix}$ , $\begin{matrix} V_{\infty i} \end{matrix}$ 的子域仍为过约束, $\begin{matrix} V_{\infty i} \end{matrix}$ ∩ $\begin{matrix} V_{\infty j} \end{matrix}$ =φ , 1≤ i, j≤ r, 按照生成顺序分别对 $\begin{matrix} V_{\infty i} \end{matrix}$ 进行处理。

过约束的几何约束系统包括一致性过约束子域和非一致性过约束子域。其中, 一致性过约束子域是指结构上过约束但几何上良约束的约束子域, 几何约束方程组中存在相容方程, 如x+y+z=1和2x+2y+2z=2, 一致性过约束的约束子域具有唯一解; 相对应地, 非一致性过约束子域是指结构上和几何上均为过约束的约束子域, 其几何约束方程组包含的不相容的约束方程导致系统是不可解的, 如2x+y+z=1和2x+3y+5z=2。识别过约束约束子域的一致性与非一致性, 普遍的做法是进行符号计算, 但效率低, 需要消耗大量的计算时间和计算空间。本文采用文献[10]中改进的ABC算法识别过约束的一致性与非一致性。由DM分解法可知 $\begin{matrix} V_{\infty} \end{matrix}$ 中饱和顶点的匹配必为最大匹配, 该最大匹配的解具有唯一性, 若转换饱和顶点的几何约束为约束方程组, 则由改进的ABC算法可获得该唯一解S。其次, $\begin{matrix} V_{\infty} \end{matrix}$ 中饱和顶点的几何约束由非饱和顶点的几何约束所替换, 使替换后的匹配仍为最大匹配, 将S代入替换后的几何约束方程组, 如果该方程组被S所满足, 则两个几何约束方程组同解, 存在相容的几何约束, 表明该子域为一致性过约束子域, 否则为非一致性过约束子域。

对于一致性过约束, 几何约束是相容的, 替换对应的几何约束方程组能够保持几何约束系统的解不变, 因此, 只保留其中的一个几何约束, 且拓扑几何约束被优先保留, 并拆卸其他的冗余几何约束; 对于非一致性过约束, 几何约束不相容, 替换将导致几何约束方程组的解并非唯一, 除只有唯一的正确解以外, 其他不相容几何约束均不符合设计意图, 因此, 输出不相容的几何约束, 并由设计者选择性地拆卸其中不符合设计意图的几何约束。如果过约束子域仅包含一致性过约束或者非一致性过约束中由设计者拆卸的几何约束恰好是 $\begin{matrix} V_{\infty} \end{matrix}$ 的饱和顶点, 那么识别过约束类型的几何约束方程组的解可作为该过约束子域的解, 这样能够降低几何约束求解的计算量。

算法3 过约束子域的处理算法

步骤1 分解过约束子域的顶点集 $\begin{matrix} V_{\infty} \end{matrix}$ 为r个不相关的子过约束域顶点集{ $\begin{matrix} V_{\infty i} \end{matrix}$ |1≤ i≤ r}, 其中 $\begin{matrix} V_{\infty i} \end{matrix}$ ∩ $\begin{matrix} V_{\infty j} \end{matrix}$ =φ , 1≤ i, j≤ r。

步骤2 按照 $\begin{matrix} V_{\infty i} \end{matrix}$ 的生成顺序计算所有 $\begin{matrix} V_{\infty i} \end{matrix}$ 的子约束域自由度DOF( $\begin{matrix} G_{\infty i} \end{matrix}$ ), 记为k。转换 $\begin{matrix} V_{\infty i} \end{matrix}$ 中饱和顶点的几何约束为方程组, 由改进ABC算法获得解S。

步骤3 由 $\begin{matrix} V_{\infty i} \end{matrix}$ 某非饱和顶点的几何约束替换与其相关联的饱和顶点的几何约束, 将解S代入替换后的几何约束方程组。

步骤4 若替换后的几何约束方程组被S所满足, 则拆卸冗余几何约束和对应的非饱和顶点。

步骤5 若几何约束方程组不能被S所满足, 对非饱和顶点的几何约束予以输出, 并由设计者拆卸不符合设计意图的冗余几何约束和顶点; 若拆卸的几何约束与饱和顶点相对应, 则设置保留几何约束的顶点为饱和顶点, 使用保留几何约束的约束方程替换冗余几何约束的约束方程, 求解替换后的几何约束方程组的解S。

步骤6 k=k-1, 若k≠ 0, 转步骤3。

步骤7 若i≠ r, i=i+1, 转步骤2; 否则, 算法终止。

3 求解实例分析

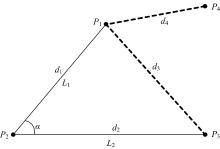
为阐述本文算法的正确性, 给出求解实例如图3所示, 已知点P_i(1≤ i≤ 4)和直线L_j(1≤ j≤ 2), 其中(P₁, P₂)、(P₂, P₃)、(P₁, P₃)和(P₁, P₄)之间的距离分别为d₁、d₂、d₃和d₄, (L₁, L₂)之间的夹角为α 。

	Figure Option View Download New Window
	图3 求解实例的草图Fig.3 Sketch map of a solving example

首先, 使用二部图模型表示该造型实例的几何约束系统, 几何基元包括:点P_i(1≤ i≤ 4)和直线L_j(1≤ j≤ 2), 确定P_i的参数为(x_i, y_i), 确定L_j的参数为(L_j₁, L_j₂); 若使用描述DisPP(A, B, d)表示点A到点B的距离为d, AngleLL(L_A, L_B, θ )表示直线L_A和L_B之间的夹角为θ 和OnLine(A, L)表示点A在直线L上, 则系统几何约束包括:

DisPP(P₁, P₂, d₁), DisPP(P₂, P₃, d₂),

DisPP(P₁, P₃, d₃), DisPP(P₁, P₄, d₄), AngleLL(L₁, L₂, a), OnLine(P₁, L₁), OnLine(P₂, L₁), OnLine(P₂, L₂),

OnLine(P₃, L₂)

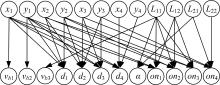
几何约束系统二部图模型见图4, 其中v_b₁、v_b₂和v_b₃为基本几何约束, 用于固定几何造型; on₁, on₂, on₃和on₄分别表示几何约束OnLine(P₁, L₁), OnLine(P₂, L₁), OnLine(P₂, L₂)和OnLine(P₃, L₂)。

	Figure Option View Download New Window
	图4 求解实例的二部图模型Fig.4 Bipartite graph model of the solving example

其次, 识别出该几何约束系统的欠、过约束子域, 由算法1获得二部图的最大匹配为:M={(x₁, v_b₁), (y₁, v_b₂), (L₁₁, v_b₃), (L₁₂, on₁), (x₂, d₁), (y₂, on₂₎, (L₂₁, α ), (L₂₂, on₃), (x₃, d₂), (y₃, on₄), (x₄, d₄)}。

再由DM分解法分解获得最大匹配, 分解后S⁺={y₄}, S^-={d₃}, 且进一步可以得到V₀={x₄, y₄, d₄}和 $\begin{matrix} V_{\infty} \end{matrix}$ ={x₁, y₁, x₂, y₂, x₃, y₃, L₁₁, L₁₂, L₂₁, L₂₂, v_b₁, v_b₂, v_b₃, d₁, d₂, d₃, α , on₁, on₂, on₃, on₄}。欠、过约束子域使用算法2进行识别。由于V₀和 $\begin{matrix} V_{\infty} \end{matrix}$ 均不为空, 所以该求解实例同时包含了欠约束子域和过约束子域。

$\begin{matrix} V_{\infty} \end{matrix}$ 包含的所有顶点不可进一步分解, 此时对 $\begin{matrix} V_{\infty} \end{matrix}$ 分解后, 不相关的过约束子域顶点集合族中仅包含 $\begin{matrix} V_{\infty 1} \end{matrix}$ = $\begin{matrix} V_{\infty} \end{matrix}$ , 由算法3计算出DOF( $\begin{matrix} G_{\infty 1} \end{matrix}$ )=-1, 表明该几何约束系统中仅存在一个冗余几何约束, 转换 $\begin{matrix} V_{\infty 1} \end{matrix}$ 中饱和顶点的几何约束为几何约束方程组, 并假设v_b₁=3, v_b₂=6, v_b₃=0, d₁=6, d₂=4, d₃=7, d₄=7和θ =π /4。此时, 使用改进的ABC算法得到该方程组的解S, 然后使用 $\begin{matrix} V_{\infty 1} \end{matrix}$ 中非饱和顶点的几何约束d₃替换与d₃相关联的饱和顶点的几何约束, 用以保证替换后的匹配仍是最大匹配, 由条件可知, 将S代入替换后的几何约束方程组时, 该方程组并不被S所满足, 可确定该过约束为非一致性过约束。且由二部图模型可得, 所有与d₃(包括d₃本身)相关联的几何约束为:d₁, d₂, d₃, on₁, on₃和on₄, 输出后由设计者拆卸不符合设计意图的几何约束。若几何约束d₃不符合设计者的设计意图, 则将d₃拆卸。

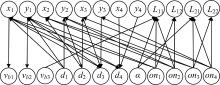同样地, V₀包含的顶点不可分解, 不相关的欠约束子域顶点集合族中仅包含 $\begin{matrix} {V_{0}}_{1} \end{matrix}$ =V₀, 由算法2计算出DOF(G₀₁)=1, 表明装配一个约束度为1且符合设计意图的几何约束即可正确求解, 若P₂和P₄之间的距离尚未明确, 则选择装配距离约束DisPP(P₁, P₄, d₅), 由于已经存在DisPP(P₁, P₄, d₄), 因此装配DisPP(P₁, P₄, d₅)无效; 若继续装配距离约束DisPP(P₂, P₄, d₅), 则由DM分解法分解装配了DisPP(P₂, P₄, d₅)的V₀时, 可得V₀为最大匹配, 表明DisPP(P₂, P₄, d₅)可用, 但并不为设计者所知, 装配约束仍然为无效约束; 若再装配距离约束DisPP(P₃, P₄, d₅), 分解后可得装配了该几何约束的V₀为最大匹配, 且该几何约束为设计者所知。此时, 输入距离参数d₅, 完成欠约束子域的处理。该实例中处理欠、过约束域后的二部图模型如图5所示。

	Figure Option View Download New Window
	图5 处理欠、过约束域后的二部图模型Fig.5 Bipartite graph model after dealing with the under-and over-constrained domains

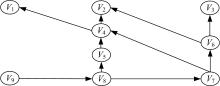
使用DM分解法可以获得该二部图的一个DM分解序列为:V₀=φ , V₁={x₁, v_b₁}, V₂={y₁, v_b₂}, V₃={L₁₂, v_b₃}, V₄={L₁₂, on₁}, V₅={x₂, y₂, d₁, on₂}, V₆={L₂₁, α }, V₇={L₂₂, on₃}, V₈={x₃, y₃, d₂, on₄}, V₉={x₄, y₄, d₄, d₅}, $\begin{matrix} V_{\infty} \end{matrix}$ =φ 。

可以看出, 处理后的几何约束系统为良约束几何约束系统。且由偏序关系能够确定系统求解序列, 其偏序关系如图6所示。

	Figure Option View Download New Window
	图6 几何约束系统求解实例的偏序关系Fig.6 Partial order relation of GCS example

根据偏序关系, 可选择一种适合的几何约束求解方法, 依顺序获得处理后的各参数并生成符合设计意图的几何造型。

4 结束语

本文从几何可解性上识别和处理几何约束系统的欠、过约束子域。采用二部图模型来表达几何约束系统, 改进基于二部图的建模方法。利用DM分解法识别出几何约束系统的欠、过约束子域。由实例证明了新建模方法的优点。提出以结点度为优先级的最优选择算法获得二部图的最大匹配, 证明了该算法的有效性。针对欠约束子域的处理, 添加约束优先级改进算法的几何约束装配机制, 并在装配几何约束的同时判定装配有效; 针对过约束子域的处理, 使用改进的ABC算法来判定过约束的一致性与非一致性, 不同类型的过约束子域采用不同的处理方法, 一致性过约束的处理方法是选择任意的冗余约束并拆卸, 而非一致性过约束的处理方法是输出过约束, 由设计者选择拆卸不符合设计意图的几何约束。最后, 通过实例证明了本文欠、过约束识别及处理算法的可行性和有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Betting B, Hoffmann C M. Geometric constraint solving in parametric computer-aided design[J]. Journal of Computing and Information Science in Engineering, 2011, 11(2): 1-9. [本文引用:1]
[2]	夏秋英. 参数化、变量化技术及其CAD系统[J]. 精密制造与自动化, 2005(1): 53-56. Xia Qiu-ying. Parametric technology, variation technology and CAD system[J]. Precise Manufacturing & Automation, 2005(1): 53-56. [本文引用:1]
[3]	Sun Wei, Ma Tie-qiang, Huang Yu-jun. Research on method of constraint conversion in feature-based data exchange between heterogeneous CAD systems[J]. Journal of Mechanical Science and Technology, 2009, 23(1): 246-253. [本文引用:1]
[4]	He Chun-hua, Zhang Xiang-wei, Lyu Wen-ge. A new approach for solving geometric constraint based on election-survey algorithm[C]//International Conference on Computer, Mechatronics, Control and Electronic Engineering (CMCE), Changchun, China, 2010: 427-430. [本文引用:1]
[5]	Cao Chun-hong, Zhang Bin, Li Wen-hui. The research based on the composite particle swarm optimization algorithm in the geometric constraint solving[J]. Journal of Image and Graphics, 2007, 12(4): 713-717. [本文引用:1]
[6]	Cao Chun-hong, Tang Chuan, Zhao Da-zhe, et al. Geometric constraint solving based on GeesePSO optimization[J]. Journal of Chinese Computer System, 2011, 32(11): 2299-2302. [本文引用:1]
[7]	Kondo K. Algebraic method for manipulation of dimensional relationships in geometric models[J]. Computer-Aided Design, 1992, 24(3): 141-147. [本文引用:1]
[8]	Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Journal on Computing, 1997, 26(5): 1484-1509. [本文引用:1]
[9]	Lin Qiang, Gao Xiao-shan, Liu Yuan-yuan. The complete method based on geometric constraint solving[J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(7): 828-834. [本文引用:1]
[10]	曹春红, 许光星. 基于改进人工蜂群算法的几何约束求解[J]. 计算机科学与探索, 2015, 9(9): 1122-1131. Cao Chun-hong, Xu Guang-xing. Geometric constraint solving based on improved artificial bee colony algorithm[J]. Journal of Frontiers of Computer Science & Technology, 2015, 9(9): 1122-1131. [本文引用:1]
[11]	王朝瑞. 图论[M]. 北京: 北京工业学院出版社, 1987: 222-229. [本文引用:1]
[12]	蒋鲲, 张岩, 潘锲. 用DM-分解求解几何约束问题[J]. 黑龙江大学自然科学学报, 2005, 22(5): 674-680. Jiang Kun, Zhang Yan, Pan Qie. Geometric constraint solving with DM-decomposition of bigraph[J]. Journal of Natural Science of Heilongjiang University, 2005, 22(5): 674-680. [本文引用:1]

2011

0.0

... 0 引言几何约束求解^[1](Geometric constraint solving,GCS)可理解为几何造型(如:产品模型、分子结构造型、工程设计用图等)设计的自动化,即给定造型的几何约束关系后,自动生成用户所需设计造型的过程 ...

0.0

. , 2005(1):53-56 DOI:doi:10.3969/j.issn.1009-962X.2005.01.018

Parametric technology, variation technology and CAD system

参数化、变量化技术及其CAD系统

Xia Qiu-ying.

夏秋英

CAD概念是1962年美国麻省理工学院(MIT)的博士生1.E.Sutherland在其博士学位论文中提出来的.CAD作为信息技术的一个重要组成部分,对加速工程和产品的开发、缩短设计与制造周期、提高质量和降低成本、增强企业市场竞争能力与创新能力发挥着重要作用.随着计算环境和计算技术的不断变革,CAD技术仍会不断地出现新的研究领域和研究课题.本文首先对两种主流CAD造型基础技术--参数化技术和变量化技术进行了阐述,然后介绍了国际上的主流CAD系统和产品谱系.这对于当前全面了解两种造型技术的技术特点以及CAD系统的选型是有所裨益的.

... 它作为现代参数化、变量化设计体系的核心,是现代化计算机辅助设计(Computer aided design,CAD)和计算机辅助制造(Computer aided manufacture,CAM)的重要标志之一^[2,3] ...

2009

0.0

2010

0.0