基于多尺度的区域生长的图像分割算法

引用本文

肖明尧, 李雄飞, 张小利, 张刘. 基于多尺度的区域生长的图像分割算法. 吉林大学学报（工学版）, 2017, 47(5): 1591-1597
XIAO Ming-yao, LI Xiong-fei, ZHANG Xiao-li, ZHANG Liu. Medical image segmentation algorithm based on multi-scale region growing. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1591-1597 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705035
Permissions

基于多尺度的区域生长的图像分割算法

肖明尧^1,², 李雄飞², 张小利², 张刘³

1.长春师范大学计算机科学与技术学院长春 130032

2.吉林大学计算机科学与技术学院长春 130012

3.吉林大学仪器科学与电气工程学院,长春 130061

通信作者:张刘(1978-),男,教授.研究方向:卫星姿态测量与控制技术,空间对接测量技术及空间遥感成像系统设计与仿真技术.E-mail:zhangliu@jlu.edu.cn

作者简介:肖明尧(1980-),男,讲师,博士.研究方向:数据挖掘与图像处理.E-mail:fengyuanqing@tom.com

基金项目:国家自然科学基金项目(61272209); “十二五”国家科技支撑计划项目(2012BAH48F02)

摘要

针对医学图像的特点,提出了一种多尺度区域生长分割算法。该算法首先利用高斯滤波器对原图像进行滤波处理,之后利用区域生长算法分别对原图像与平滑图像进行分割操作,最后将两个分割图谱进行比对,获得最终的分割结果。进行区域生长算法时,从背景区域选择一个像素作为初始种子点进行区域生长。该方法的优势为噪音具有较好鲁棒性,初始种子点选取规则简单。该方法同样适合于其他背景简单、目标区域复杂的图像分割情形。为了选取合适分割阈值,提出了最大梯度概念。利用图像的最大梯度矩阵的统计特性,将阈值选取问题转化为求最小值问题。实验表明,该方法能够准确地获得医学图像的分割结果。

关键词: 计算机应用; 医学图像分割; 区域生长; 多尺度; 梯度

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2017)05-1591-07

Medical image segmentation algorithm based on multi-scale region growing

XIAO Ming-yao^1,², LI Xiong-fei², ZHANG Xiao-li², ZHANG Liu³

1.College of Computer Science and Technology, Changchun Normal University, Changchun 130032, China

2.College of Computer Science and Technology, Jilin University, Changchun 130012,China

3.College of Instrumentation & Electrical Engineering, Jilin University,Changchun 130061,China

Abstract

Considering the characteristics of medical images, a multi-scale region growing segmentation algorithm is proposed. First, the original image is smoothed by a Gaussian filter. Then, the region growing segmentation is performed on both the original image and the smoothed image. Finally, the two obtained segmentation maps are compared to get the final segmentation. In the process of region growing segmentation, a pixel in the background region is selected as the initial seed for region growing. The advantages of the proposed algorithm are the robustness to noises and easiness of initial seed selection. This method is also suitable to other segmentation applications, in which background region is simple but target region is complex. In order to select an appropriate threshold, the concept of Maximum Gradient Transform (MGT) is proposed. The issue of threshold selection is converted into a minimization problem with the assistance of the statistical properties of the transformation matrix. Experiment results show that the proposed algorithm can obtain accurate medical image segmentation results.

Key words: computer application; medical image segmentation; region growing; multi-scale; gradient

Show Figures

0 引言

图像分割是指将图像中空间位置连通的、且具有相似视觉形态的像素聚类在一起, 并提取感兴趣区域(Regions of interest, ROI)的技术的统称, 是计算机视觉领域内一个重要的研究课题^{[1, 2]}。本文探讨医学图像的分割问题, 与传统的分割目的不同, 主要研究如何将组织区域与背景区域进行有效分离。它已经成为多种医学图像处理的基础, 如三维重建面绘制^[3]、多模态医学图像配准^{[4, 5]}、医学图像质量评价^[6]等。对于图像分割算法的分类方式尚无统一标准。文献[7]给出了较为清晰的分类方法, 作者将现有的图像分割分为局部过滤方法、活动轮廓模型(或者称之为Snake模型)、区域生长类或者合并区域类、全局优化模型类。区域生长类算法最初是由Adams等^[8]提出的, 其基本原理是首先选取种子点集, 并与周围与之形态(灰度、纹理等)相似的像素进行合并, 不断更新种子点集, 迭代合并周围相似像素, 直到满足生长停止条件为止。因其兼顾了像素特征分布和空间分布, 所以, 该类算法多数情况下能够得到较好的视觉分割效果。更重要的是, 该方法的分割结果能够提供封闭的区域, 对于区域内部的变化具有较好的鲁棒性^[9]。医学图像大致可以分为背景区域和目标组织区域两部分。其中, 背景区域比较平滑, 而目标组织相对复杂, 所以该方法较适合于医学图像分割^{[10, 11]}。但传统的区域生长法易受噪音的影响, 形成有洞区域。针对该问题, 通常的做法是首先进行高斯滤波, 将噪音去除, 然后再进行区域生长算法分割^{[12, 13]}。这种做法往往存在两个问题:容易造成边缘模糊, 影响分割效果^[14]; 若降噪不彻底, 同样会造成分割区域有洞的情况发生。为了消除有洞的情况, 文献[13]提出在分割的基础上做闭操作, 将洞去掉。

本文提出了一种针对于医学类图像的分割算法。该方法引入了多尺度图像表示的概念。多尺度表示可同时提供图像的不同尺度表示, 在不同尺度上可得到不同的分割结果, 且各具优势。若将各个分割结果进行整合, 则可显著提高分割质量。同时, 利用邻差变换的统计信息确定分割阈值。该分割方法具有初始种子点选取规则简单、不受噪音影响等特点。

1 图像分割分析

1.1 问题描述

令集合R表示整个图像区域, 对R的分割可以看作将R分成N个满足以下5个条件的非空子集R₁, R₂, …, R_N。

(1) $\begin{matrix} \overset{N}{⋃_{i = 1}} \end{matrix}$ R_i=R

(2)若i≠ j, 则R(i)∩ R(j)=∅

(3)P(R(i))=TRUE其中, i=1, 2, …, N

(4)若i≠ j, 则P(R(i)∪ R(j))=FALSE

(5)∀ i=1, 2, …, N, R_i是连通的。

1.2 传统区域生长法

区域生长法的步骤如下:

(1)选择一个种子点, 将其纳入到队列Q中。

(2)检查周围所有点像素, 并判断其是否与种子点相似, 如果相似, 则将其纳入到Q中, 否则不予处理。

(3)将队列Q中的第一个元素弹出, 并加入到集合R₁中。并检查Q是否为空, 若不为空, 则将当前Q中的第一个元素作为种子点, 并重复步骤(2); 否则, 将尚未列入R₁中的元素纳入到R₂。

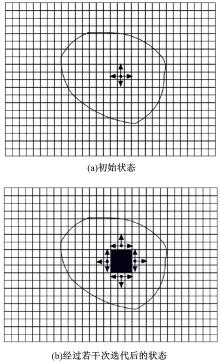
	Figure Option View Download New Window
	图1 区域生长分割示例Fig.1 Illustration of region growing

图1为区域生长的一个实例。经过不断的迭代, 相似的元素则不断纳入到种子点所在的区域中。

命题1 对于任意图像R, 初始种子点为p, 经过区域生长后, p∈ R₁, 则R₁是连通的。

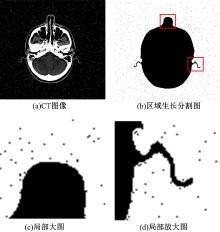
通过命题1可知, 传统区域生长算法只能保证初始种子点所在的区域是连通的, 而无法保证其他区域也是连通的。该算法容易受到噪音或不规则边缘的影响, 往往会将噪音划分成孤立的小区域。同时, 也会在边界处产生很多小的孤立点。具体如图2所示。图2(a)为一幅脑部CT图像, 本文希望通过分割算法能将组织部分与背景部分有效分离。图2(b)为区域生长算法得到的结果, 种子点选在了图像的左上角点。图2(c)(d)为图2(b)中的方框处的放大图。实际上, 在图2中这些孤立区域应均属于背景区域。为了解决该问题, 本文提出了多尺度区域生长算法。

	Figure Option View Download New Window
	图2 区域生长图像分割效果Fig.2 Segmentation of region growing

2 算法描述

2.1 最大梯度变换

本文提出一种新的图像变换方式— — 最大梯度变换(Maximum gradient transform, MGT), 该变换可以反映图像中各个像素与邻差像素的最大差别。

对于给定图像I, p为图像I内的像素坐标, 则MGT定义为如下形式:

$\begin{matrix} MG T_{f} (p) = \max_{q \in w_{p}} (| I_{p} - I_{q} |) \end{matrix}$ （1）

式中:w_p为以p的邻域。

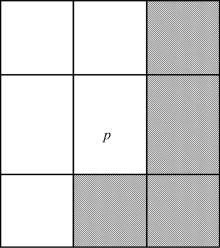
w_p内的元素包含p的右上角、右侧、右下角及下面。如图3所示, w_p部分为纹理填充区域。

	Figure Option View Download New Window
	图3 w_p示意图Fig.3 Illustration of w_p

w_p没有选择像素p的八邻域的原因在于, 通过实验发现与选择八邻域时对于阈值的选择极为相近, 而当前w_p的设置则比八邻域降低一半的时间开销。

为了方便计算, 给出对于图像I的邻差变换的另外一种形式:

$\begin{matrix} \begin{matrix} MGT (I) = \max (| MG T_{i} (I) |) \\ i = 1, 2, 3, 4 \end{matrix} \end{matrix}$ （2）

将D(I)记为图像I的邻差矩阵, 其大小与I一致。在式(2)中, D_i(I)的大小与图像I相同, 每一元素表示图像I对应像素与其成iπ /4, 且紧邻的像素的灰度之差的计算公式为:

${\begin{matrix} D \end{matrix}}_{i} (I) = I° C_{i} i = 1, 2, 3, 4$ (3)

式中:􀳱表示卷积操作; C_i为3× 3大小的核函数, 具体定义如下:

$\begin{matrix} \begin{matrix} C_{1} = (\begin{matrix} 0 & 0 & - 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{matrix}), C_{2} = (\begin{matrix} 0 & 0 & 0 \\ 0 & 1 & - 1 \\ 0 & 0 & 0 \end{matrix}), \\ C_{3} = (\begin{matrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & - 1 \end{matrix}), C_{4} = (\begin{matrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & - 1 & 0 \end{matrix}) 。 \end{matrix} \end{matrix}$

2.2 算法框架

考虑到图像中往往受到噪音、弱边缘的影响, 使用传统的区域分割算法容易产生孤立区域, 所以本文使用其改进算法— — 多尺度区域分割法。在该算法中, 需要确定分割阈值, 该阈值对分割结果将产生较大的影响。所以, 本文通过邻差变换获取图像的变换矩阵, 并通过变换矩阵的统计信息获取分割阈值。分割的具体步骤如下:

(1)对图像I进行高斯滤波, 得到平滑图像I'=I􀳱K。其中, K为高斯核函数。

(2)根据式(2), 对待分割图像I和I'做最大梯度变换, 得到最大梯度变换矩阵MGT(I)和MGT(I')。

(3)根据MGT(I)和MGT(I')的统计信息获得分割阈值λ 和λ '。

(4)分别对原始图像I和平滑图像I'进行区域生长分割, 其结果分别保存在RG和RG'中。

(5)对分割结果RG和RG'进行整合, 获得最终的分割结果Map。

矩阵Map即图像I的分割结果, 该矩阵中, 黑色部分为目标区(灰度值用0填充), 白色为背景区域(灰度值用1填充)。

步骤(1)的目的在于图像的多尺度表示, 即原图像I与平滑图像I'是图像I的不同尺度上的表示。其中, I'中已经消除了图像I中的部分噪音, 但同时也弱化了原始图像的边缘, 所以其分割结果RG'中能有效消除噪音的影响, 但在区域边缘处分割效果较差。而原始图像的分割结果RG受噪音影响较大, 分解效果差, 但在区域边缘处效果较好。因此, 在步骤(5)中, 将二者进行整合, 则可综合二者的优势。

2.3 阈值选择

本文的算法是要针对于背景区域简单、前景区域复杂的情况。通过观察发现, 背景部分的颜色接近黑色, 所以该部分内像素I_p的MGT值应该尽量小。因此, 可以通过最小化该区域内MGT值来寻找最优阈值。但注意到, 应尽量找全所有背景区域, 所以, 还需要最大化背景区域像素数量。综上所述, 将阈值的设定转化为如下最小化问题。

$\begin{matrix} λ = \underset{j}{\arg} \{\min (\frac{\sum_{p \in Bj} MGT (I_{p})}{N_{Bj}})\} \end{matrix}$ (4)

式中:N_Bj为阈值设定为j的背景区域的像素的数量; MGT(I_p)为邻差矩阵MGT(I)在p处的取值。

同样, 对于I', 利用式(4)可得到相应的λ '。式(4)则是通过最小化背景区域内MGT值之和以及最大化背景区域大小来实现最优阈值选取的。

2.4 分割结果整合

在本文算法中, 需要使用区域生长对源图像I和平滑图像I'进行分割, 得到分割结果分别为RG和RG', 需要对两个结果进行整合, 以获得最终的融合结果Map。

首先, 比较RG和RG'之间的差异, 即

$\begin{matrix} α = RG \oplus R G^{'} (5) \end{matrix}$

式中:􀱇为异或运算符。

当且仅当RG和RG'内对应的元素不同时, α 矩阵内对应的元素为1。对于任意p, 若α (p)=1, 说明该像素需要重新进行分类, 此时, 该像素的分类标签为:

$\begin{matrix} Map (p) = \underset{i = 0, 1}{\arg} \max \{\sum_{q \in w_{p}} Ind (RG (p) = i)\} \end{matrix}$ （6）

式中:Ind(RG(p)=i)为指示函数, 当RG(p)=i为真时, 该函数取值为1; 否则为0。

如果α (p)=0, 表示RG(p)=RG'(p), 此时有

$\begin{matrix} Map (p) = RG (p) (7) \end{matrix}$

综合式(6), 图像分割的整合公式可以定义为:

$\begin{matrix} \begin{matrix} Map (p) = \\ \{\begin{matrix} \underset{i = 0, 1}{\arg} \max {\sum_{q \in w_{p}} Ind (RG (p) = i)}, α (p) = 1 \\ RG (p), α (p) = 0 \end{matrix} \end{matrix} \end{matrix}$ （8）

3 实验结果与分析

3.1 分割结果客观评估指标

设图像I为分割测试图像, G和R都是二值矩阵, 分别表示为人工分割结果和算法分割结果, I中像素(x, y)可以被分为以下4个类别:

真正类:G(x, y)=1∧ R(x, y)=1

假正类:G(x, y)=0∧ R(x, y)=1

假负类:G(x, y)=1∧ R(x, y)=0

真负类:G(x, y)=0∧ R(x, y)=0

根据这个分类标准, 可统计出整幅图像的真正实例数量、假正实例数量、假负实例数量和真负实例数量, 分别标记为TP、FP、FN、TN, 关系如表1所示。

表1 混淆矩阵 Table 1 Confusion matrix

根据表1, 可以得到两项指标:

$\begin{matrix} \begin{matrix} tpr = \frac{TP}{TP + FN} (9) \\ tnr = \frac{TN}{TN + FP} (10) \end{matrix} \end{matrix}$

式中:tpr为真正率, 表示实际正类被分类正确的比率; tnr为真负率, 表示实际负类被分类正确的比率。二者的取值范围均为[0, 1], 且取值越大表明图像分割质量越好。

3.2 实验结果

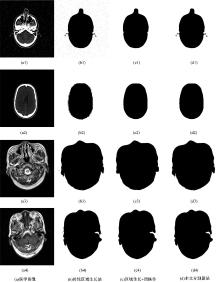
图4为不含噪音的医学图像的分割结果, 第1列为4幅原始图像, 其中, 图4(a1)(a2)下载自Vanderbilt大学的图像配准评估项目网站, 是两幅不同部位的CT切片, 图4(a3)(a4)是由吉林大学第二附属医院提供的MR-T1和MR-T2切片。第二列为传统区域生长算法的分割结果, 第三列为区域生长后进行闭操作处理所得结果, 第四列为本文分割算法所得的结果。

	Figure Option View Download New Window
	图4 医学图像分割结果Fig.4 Segmentation of medical images

从图4的分割结果来看, 传统的区域分割对于噪音和孤立边缘区域的处理是不理想的:由图4(b1)可以看到, 在背景区域存在大量的孤立点, 这是因为在原始图像中存在大量的噪音。在图4(b2)中, 边界处也存在较多孤立区域, 导致背景区域内有洞, 目标区域不连通。注意到图4(a2)的背景区域内灰度值均为0, 背景区域不含任何噪音, 所以在图4(b2)内没有出现因为噪音像素引起的孤立区域。而在图4(b3)(b4)中, 不仅在两个区域的边界处出现了孤立点, 而且在背景区域出现了孤立点。而对于区域生长+闭操作算法, 能够有效去除孤立点, 而且使得两个区域的边界更为平滑。但也降低了分割质量, 比如图4(c1), 因为闭操作, 将耳骨信息去除了, 这样的情况同样出现在图4(c3)(c4)中。而本文提出的多尺度区域生长算法则对噪音和孤立边缘进行了很好的处理, 在图4(d1)(d2)中, 虽然两个区域的边界处仍然不平滑, 但是其周围的孤立区域已经全部去除。在图4(d3)(d4)中也去除了所有的孤立点。从主观判断上来看, 本文算法在处理孤立点方面比传统区域生长算法更具优势。而在边界保真方面, 比区域生长+闭操作算法表现更好。

使用tpr和tnr对图4中的4组分割结果进行定量评估, 结果如图5所示。

	Figure Option View Download New Window
	图5 测试图像客观评价结果Fig.5 Objective evaluation of test images

由图5可知, tpr指标的评价结果认为本文算法的表现最优, 其次为传统区域生长, 最后为区域生长+闭操作算法。其原因在于本文算法能够修正传统算法在图像边界处的分割误差。而闭操作导致欠分割情况的出现, 所以, 区域生长+闭操作算法的tpr指标比传统的区域生长算法的低。tnr指标中, 区域生长+闭操作算法的得分最高, 其原因同样是因为欠分割的结果, 尤其在最后一组中, 其得分达到了100%。而本文算法在tpr和tnr上的得分基本持平, 说明不存在明显的过分割和欠分割, 且两项指标得分均较高, 从而说明了本文算法的有效性。

4 结束语

提出了一种改进的区域生长分割算法— 多尺度区域分割算法。该算法首先利用高斯滤波器对原图像进行滤波处理, 之后利用区域生长算法分别对原图像与平滑图像进行分割操作, 最后将两个分割图谱进行比对, 获得最终的分割结果。该算法种子点选取规则简单, 对噪音具有较强的鲁棒性, 保证背景区域和目标区域均为不带洞的连通区域。为了实现分割阈值的自动选取, 提出了最大梯度的概念, 通过统计最大梯度矩阵的分布规律, 将阈值选取问题转化为优化问题。本文实验表明, 在原图像有、无噪音的情况下, 该算法均可得到较好的分割效果, 没有出现明显的过分割或欠分割现象。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Hojjatoleslami S A, Kittler J. Region growing: a new approach[J]. IEEE Transactions on Image Processing, 1998, 7(7): 1079-1084. [本文引用:1]
[2]	张明慧, 卢振泰, 张娟, 等. 基于多图谱活动轮廓模型的脑部图像分割[J]. 计算机学报, 2015, 38(118): 1-10. Zhang Ming-hui, Lu Zhen-tai, Zhang Juan, et al. Brain image segmentation based onmultiple atlas active contour model[J]. Chinese Journal of Computers, 2015, 38(118): 1-10. [本文引用:1]
[3]	何晖光, 田捷, 赵明昌, 等. 基于分割的三维医学图像表面重建算法[J]. 软件学报, 2002, 13(2): 219-226. He Hui-guang, Tian Jie, Zhao Ming-chang, et al. A 3D medical imaging surface reconstruction scheme based on segmentation[J]. Journal of Software, 2002, 13(2): 219-226. [本文引用:1]
[4]	Rueckert D, Aljabar P. Nonrigid registration of medical images: theory, methods, and applications[J]. Signal Processing Magazine, 2010, 27(4): 113-119. [本文引用:1]
[5]	许鸿奎, 江铭炎, 杨明强. 基于改进光流场模型的脑部多模医学图像配准[J]. 电子学报, 2012, 40(3): 525-529. Xu Hong-kui, Jiang Ming-yan, Yang Ming-qiang. Registration of multimodal brain medical images based on improved optical flow model[J]. Acta Electronica Sinica, 2012, 40(3): 525-529. [本文引用:1]
[6]	Greve D N, Fischl B. Accurate and robust brain image alignment using boundary-based registration[J]. Neuroimage, 2009, 48(1): 63-72. [本文引用:1]
[7]	Song C Z, Yuille A. Region competition: unifying snakes, region growing, and Bayes/MDL for multiband image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(9): 884-900. [本文引用:1]
[8]	Adams R, Bischof L. Seeded region growing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(6): 641-647. [本文引用:1]
[9]	徐杰, 施鹏飞. 基于相位一致与区域生长的自然彩色图像分割[J]. 电子学报, 2004, 32(7): 1203-1205. Xu Jie, Shi Peng-fei. Natural color image segmentation based on phase congruency and region growing[J]. Acta Electronica Sinica, 2004, 32(7): 1203-1205. [本文引用:1]
[10]	Mehnert A, Jackway P. An improved seeded region growing algorithm[J]. Pattern Recognition Letters, 1997, 18(10): 1065-1071. [本文引用:1]
[11]	Fan J, Yau D Y, Elmagarmid A K, et al. Automatic image segmentation by integrating color-edge extraction and seeded region growing[J]. IEEE Transactions on Image Processing, 2001, 10(10): 1454-1466. [本文引用:1]
[12]	Shan J, Cheng H D, Wang Y. A novel automatic seed point selection algorithm for breast ultrasound images[C]//The 19th International Conference on Pattern Recognition(ICPR2008), Tampa, Florida, USA, 2008: 1-4. [本文引用:1]
[13]	Pan Z, Lu J. A Bayes-based region-growing algorithm for medical image segmentation[J]. Computing in Science & Engineering, 2007, 9(4): 32-38. [本文引用:1]
[14]	Lin Z, Jin J, Talbot H. Unseeded region growing for 3D image segmentation[J]. Journal of Trauma, 2002, 24(11): 938-945. [本文引用:1]

1998

0.0

... 0 引言图像分割是指将图像中空间位置连通的、且具有相似视觉形态的像素聚类在一起,并提取感兴趣区域(Regions of interest,ROI)的技术的统称,是计算机视觉领域内一个重要的研究课题^[1,2] ...

2015

0.0

. 2015, 38(118):1-10 DOI:doi:10.11897/SP.J.1016.2016.01490

Brain image segmentation based onmultiple atlas active contour model

基于多图谱活动轮廓模型的脑部图像分割

Zhang Ming-hui , Lu Zhen-tai , Zhang Juan

张明慧, 卢振泰, 张娟

丘脑、海马体、伏隔核、尾状核等关键脑结构的位置、体积、形态等的变化与多种脑部疾病息息相关，对其精准分割是进行相关定量分析的前提。然而在磁共振图像中这些结构对比度不高、边界模糊，传统方法只是利用了标号图像，没有考虑到待分割图像、先验信息等，因无法实现准确分割。文中将多图谱配准与活动轮廓模型相结合，提出了一种新的多图谱活动轮廓模型框架，有效地利用了图谱的先验信息和待分割图像的灰度信息，将多图谱的形状先验项引入到活动轮廓模型中，并在融合标号图像的过程中利用活动轮廓模型校正配准引起的误差，可以得到光滑、准确的分割结果。该框架包含3个部分：第1部分为图谱先验项，利用配准的局部相似性作为权重融合多个图谱的信息；第2部分为数据项，利用待分割图像的局部信息，可以校正配准中的误差；第3部分为平滑项，用于保证曲线在演化过程中的平滑。大量的实验表明了该方法的有效性和准确性。

2002

0.0

. 2002, 13(2):219-226

A 3D medical imaging surface reconstruction scheme based on segmentation

基于分割的三维医学图像表面重建算法

He Hui-guang , Tian Jie , Zhao Ming-chang

何晖光, 田捷, 赵明昌

... 它已经成为多种医学图像处理的基础,如三维重建面绘制^[3]、多模态医学图像配准^[4,5]、医学图像质量评价^[6]等 ...

2010

0.0

... 它已经成为多种医学图像处理的基础,如三维重建面绘制^[3]、多模态医学图像配准^[4,5]、医学图像质量评价^[6]等 ...

2012

0.0

. 2012, 40(3):525-529 DOI:doi:10.3969/j.issn.0372-2112.2012.03.019

Registration of multimodal brain medical images based on improved optical flow model

基于改进光流场模型的脑部多模医学图像配准

Xu Hong-kui , Jiang Ming-yan , Yang Ming-qiang.

许鸿奎, 江铭炎, 杨明强

Registration method based on optical flow model is very suitable to time-sequence images,but the assumption of constant brightness at a point makes it only be used to make registration for signal-modal images.So an exact histogram specification method is proposed to transform MR-PD model to MR-T2 modal before registration based on optical flow model.If the difference between two images is large the registration result could not be ideal because this registration method is mainly used to correct the light deformation between time-sequence images,so information which reflects the structural feature of image is taken to improve optical flow model,that is,image landmarks are utilized to produce an additional external-force for optical flow model to get ideal registration parameters.Experimental results demonstrate that the improved method can realize accurate registration of multi-modality time-sequence MR images between which there is large difference.

基于光流场模型的配准其常亮假设的光流场约束要求待配准的源图像和目标图像具有一致的灰度,因而只适用于单模态图像之间的配准,为此使用基于排序的精确直方图规定化对脑部MR-PD图像进行模态变换,完成与MR-T2图像之间的灰度映射.由于此配准方法主要用来寻找时间序列图像中的细小形变,当待配准的两图像差异较大时就不能取得满意的配准效果,为此使用能反映图像结构的标记点构造附加的外力对光流场模型加以改进,以获得更理想的配准参数.实验证明,本文方法能够实现具有较大差异的脑部MR多模序列图像之间的准确配准.

... 它已经成为多种医学图像处理的基础,如三维重建面绘制^[3]、多模态医学图像配准^[4,5]、医学图像质量评价^[6]等 ...

2009

0.0

... 它已经成为多种医学图像处理的基础,如三维重建面绘制^[3]、多模态医学图像配准^[4,5]、医学图像质量评价^[6]等 ...

1996

0.0

1994

0.0

... 区域生长类算法最初是由Adams等^[8]提出的,其基本原理是首先选取种子点集,并与周围与之形态(灰度、纹理等)相似的像素进行合并,不断更新种子点集,迭代合并周围相似像素,直到满足生长停止条件为止 ...

2004

0.0

. 2004, 32(7):1203-1205 DOI:doi:10.3321/j.issn:0372-2112.2004.07.036

Natural color image segmentation based on phase congruency and region growing

基于相位一致与区域生长的自然彩色图像分割

Xu Jie , Shi Peng-fei.

徐杰, 施鹏飞

A new method for meaningful regions segmentation in natural color image is proposed in this study.After edge detecting in term of phase congruency,long edge lines are clustered using K-means algorithm based on the joint distribution of their color in image space and in color space to get meaningful seeds,while short ones are merged to eliminate the negative affection causing trivial features in images.Region growing technique is employed in color space to achieve the final segmentation results with the properly selected seeds.The proposed method overcomes the disadvantage of traditional region growing method,and applies it to color images.The meaningful segmentation results are consistent with those executed by people and have shown feasibility and effectiveness to various natural color images.

提出一种自然彩色图像中有意义区域的分割方法.利用相位一致模型检测图像边界,根据边界颜色在图像空间及色彩空间的联合分布,对长边界进行K-means聚类形成有意义的种子生长点,合并短边界以克服局部细节的干扰,最后区域生长方法作用于色彩空间得到封闭的分割区域.算法克服了传统区域生长算法缺少区域模型的局限性,同时将其成功应用到彩色图像,并得到与视觉判断相一致的有意义的分割结果.实验结果显示了所提方法对于不同自然彩色图像的有效性与适应性.

... 更重要的是,该方法的分割结果能够提供封闭的区域,对于区域内部的变化具有较好的鲁棒性^[9] ...

1997

0.0

... 其中,背景区域比较平滑,而目标组织相对复杂,所以该方法较适合于医学图像分割^[10,11] ...

2001

0.0

... 其中,背景区域比较平滑,而目标组织相对复杂,所以该方法较适合于医学图像分割^[10,11] ...

2008

0.0

... 针对该问题,通常的做法是首先进行高斯滤波,将噪音去除,然后再进行区域生长算法分割^[12,13] ...

2007

0.0

... 针对该问题,通常的做法是首先进行高斯滤波,将噪音去除,然后再进行区域生长算法分割^[12,13] ...

2002

0.0

... 这种做法往往存在两个问题:容易造成边缘模糊,影响分割效果^[14] ...