基于谱分解的不确定数据聚类方法

引用本文

李嘉菲, 孙小玉. 基于谱分解的不确定数据聚类方法. 吉林大学学报（工学版）, 2017, 47(5): 1604-1611
LI Jia-fei, SUN Xiao-yu. Clustering method for uncertain data based on spectral decomposition. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1604-1611 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705037
Permissions

基于谱分解的不确定数据聚类方法

李嘉菲^1,², 孙小玉^1,²

1.吉林大学符号计算与知识工程教育部重点实验室,长春 130012

2.吉林大学计算机科学与技术学院,长春130012

作者简介:李嘉菲 (1976-),女,副教授,博士.研究方向:信息融合.E-mail:jiafei@jlu.edu.cn

基金项目:吉林省科技厅发展计划项目(20130206046GX, 20140101201JC); 国家自然科学基金项目(61133011, 61472161,61170092, 60973088, 61202308)

摘要

提出了一种基于谱分解的不确定数据聚类方法,利用数据本身的潜在关联,探寻不确定表象下底层数据记录的真实协方差结构。根据协方差结构,使用基于谱分解的数据分析方法,获取锐化降噪后的数据,再将此数据进行聚类分析。对比实验结果表明:本方法得到的聚类质量显著提高,RMS均方根误差以及CH指标结果均优于传统方法。

关键词: 人工智能; 不确定数据; 谱分解; 聚类; 数据降噪; 协方差结构

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2017)05-1604-08

Clustering method for uncertain data based on spectral decomposition

LI Jia-fei^1,², SUN Xiao-yu^1,²

1.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012, China

2.College of Computer Science and Technology, Jilin University, Changchun 130012, China

Abstract

A clustering method for uncertain data based on spectral decomposition was proposed. The method was applied to explore the true covariance structure of data records behind the uncertain representation under the natural potential association of the data. The data analysis method based on spectral decomposition can get the sharpening data according to the covariance structure. Then, clustering analysis of the sharpening data is carried out. The comparison experiment results show that, using the proposed method, the clustering quality improves significantly; the results of root mean square error and CH index are all better than that obtained using the traditional method.

Key words: artificial intelligence; uncertain data; spectral decomposition; clustering; data sharpening; covariance structure

Show Figures

0 引言

随着各种新型信息发布方式的不断涌现, 以及云计算、物联网等技术的快速发展, 数据正以前所未有的速度在不断地增长和积累, 大数据时代已经到来^[1]。在大数据时代的背景下, 庞大的数据处理量, 相异的数据来源, 以及不同数据类型的出现, 为挖掘数据的潜在价值造成了很大的困难。而其中涌现的不确定数据更为数据分析带来了阻碍, 如何有效挖掘这种不确定数据已成为研究热点。数据的不确定性来源于多种情况, 物理仪器采集数据所产生的误差, 环境状况对数据的影响, 网络传输中受到带宽、传输延时等因素的干扰^[2], 以及出于隐私保护的目的等都可能导致数据不确定性的产生^[3]。数据不确定性的表现形式分为两种, 即存在级的不确定性和属性级的不确定性^[4]。存在级不确定性代表元组的不确定性, 属性级不确定性代表元组数据值的不确定性, 数据挖掘领域多考虑的是属性级的不确定性^[5]。

由于传统聚类方法在处理不确定数据时产生很多误差, 聚类结果对不确定性程度表现得非常敏感。所以, 近年来针对不确定数据聚类相应提出了许多改进性聚类算法。Kriegel等^[6]通过改进DBSCAN算法^[7]提出了基于密度的不确定数据聚类算法FDBSCAN, 并且改进了OPTICS算法, 提出了FOPTICS算法^[8]; Ngai等^[9]提出了利用MBR最小边界矩形以及剪枝策略的UK-means算法; Lee等^[10]在UK-means的基础之上, 提出了计算量大幅降低的CK-means算法; 而后李云飞等^[11]根据CK-means再次提出改进, 简化距离计算, 提高算法效率。除此之外, 不确定数据的研究也扩大到不确定数据流的方向上, Aggarwal等^[12]提出了扩展CF结构的UMicro算法, 并针对高维不确定数据流提出了投影聚类方法, 解决了高维数据聚类所面临的一定问题^[13]; 曹振丽等^[14]也提出一种基于高斯混合模型的不确定数据流聚类方法。

综上所述, 现有的不确定数据的聚类方法大多是根据传统的处理确定性数据的聚类算法改进而成, 它们主要存在以下的问题:①算法虽然提升了不确定数据的聚类质量, 但聚类结果依旧受误差影响严重。②在处理较高维不确定数据时, 由于不确定性导致高维数据的稀疏性加重, 聚类效果并不理想。③没有从不确定性根源上降低数据的不确定性, 方法适用性弱。为解决上述问题, 本文提出了一种基于谱分解的不确定数据聚类方法Feature Decomposition-means(FD-means), 其中谱分解又称特征分解, 该方法将利用数据本质上的潜在关联, 探寻不确定表象下底层数据记录的真实协方差结构; 再根据获得到的真实协方差结构, 使用基于谱分解的数据分析方法, 提取数据的主要特征; 然后, 通过特征值的有效选取及对应的特征向量得到数据转换矩阵, 经过投影锐化产生降噪后的数据。最后, 将处理结果进行聚类分析, 从而完成不确定数据的聚类。

1 准备工作

1.1 底层数据的真实协方差结构

在概率论和统计学中, 经常使用协方差衡量两个变量的总体误差, 协方差也可以被简单地理解为变量的关联程度。而在数据挖掘领域, 利用协方差可以计算数据内部不同属性间的关联程度。数据的协方差结构是极其重要的信息, 当数据中的不同属性来自于相互独立的来源时, 使用协方差结构降低不确定性将成为可能。并且它也是本方法中后续处理过程的基础。

由于在实际的应用中, 人们通常只能得到数据的不确定表示, 而无法获取数据的真值。所以如何探寻不确定表象下底层数据记录的真实协方差结构将成为关键。无论不确定性存在与否, 这种数据本质上存在的关联都不会被改变。如果可以获取到不确定表象下数据真实的协方差结构, 就等同于获取到真实数据中属性间的关联。

1.2 锐化降噪原理

在获取了底层数据的真实协方差结构之后, 如何利用协方差结构获取数据主要成分, 如何极大程度地保留主要信息将成为重点。本文将使用基于谱分解的方法, 分析协方差结构, 探究主要信息所在维度, 并以此提取数据主要特性和有效降低数据不确定性。其原理是将高维向量通过一个特殊的转换矩阵, 投影到低维的向量空间中, 表征为低维向量, 这个过程仅仅损失了一些次要信息, 而很大程度保留了主要且密切关联的信息, 有效去除信息冗余和噪音。

2 FD-means聚类方法

第一步, 获取不确定数据的真实协方差结构, Aggarwal在多维锐化不确定数据表示的文章中提出了一种方法可以用于获取所需的协方差结构^[15], 本文将引用这种方法。

首先给出一些符号和定义, 假定数据集中包含N条均值表示为 $\begin{matrix} {\bar{M}}_{1} \end{matrix}$ … $\begin{matrix} {\bar{M}}_{N} \end{matrix}$ 的不确定性记录, 对应的概率分布函数表示为 $\begin{matrix} {\bar{f}}_{1} \end{matrix}$ (· )… $\begin{matrix} {\bar{f}}_{N} \end{matrix}$ (· )。并假定数据记录的第j个元素表示为m_ij, 第i条记录的第j个元素的概率分布表示为f_ij(· )。接下来将数据记录 $\begin{matrix} {\bar{M}}_{i} \end{matrix}$ 第j维的源值表示为s_ij, 由r_ij加上m_ij得到s_ij的值。因此, r_ij表示在构造分布f_ij(· )的均值过程中产生的噪音。由此可以给出:

$\begin{matrix} \begin{matrix} s_{ij} = m_{ij} + r_{ij} (1) \\ m_{ij} = s_{ij} - r_{ij} (2) \end{matrix} \end{matrix}$

将数据库 $\begin{matrix} {\bar{M}}_{1} \end{matrix}$ … $\begin{matrix} {\bar{M}}_{N} \end{matrix}$ 第j维对应的随机变量表示为 $\begin{matrix} {\hat{M}}_{j} \end{matrix}$ 。因此相应的数据记录显示的N个可能值被表示为m₁_j, …, m_Nj。注意, $\begin{matrix} {\hat{M}}_{i} \end{matrix}$ 表示第i行代表一个实例, $\begin{matrix} {\hat{M}}_{j} \end{matrix}$ 表示一个随机变量, 前者对应的是[m_ij]的行向量, 后者对应的是[m_ij]的列向量。类似的, 将对应于源数据第j维的真值[s_ij]的随机变量表示为 $\begin{matrix} {\hat{S}}_{j} \end{matrix}$ 。对应于[r_ij]的第j维的随机变量表示为 $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ 。接下来, 可以有:

$\begin{matrix} {\hat{M}}_{j} = {\hat{S}}_{j} - {\overset{^{}}{R}}_{j} (3) \end{matrix}$

随机变量 $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ 与随机变量 $\begin{matrix} {\hat{S}}_{j} \end{matrix}$ 对应的真实记录值是相互独立的。这是获取底层数据记录真实协方差结构的关键性假定。接下来, 将源数据第j维和第k维的协方差表示为Cov( $\begin{matrix} {\hat{S}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{S}}_{k} \end{matrix}$ ), 并希望由Cov( $\begin{matrix} {\hat{M}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{M}}_{k} \end{matrix}$ )和Cov( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{R}}_{k} \end{matrix}$ )得到Cov( $\begin{matrix} {\hat{S}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{S}}_{k} \end{matrix}$ ), 它将被用于构造真实协方差矩阵[s_ij]。

获取源数据真实协方差结构的求解公式如下:

$\begin{matrix} Cov ({\hat{M}}_{j}, {\hat{M}}_{k}) = Cov ({\hat{S}}_{j}, {\hat{S}}_{k}) + Cov ({\hat{R}}_{j}, {\hat{R}}_{k}) \end{matrix}$ （4）

式(4)的证明过程可以详见文献[14]。如果要使用上述公式来估计协方差Cov( $\begin{matrix} {\hat{S}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{S}}_{k} \end{matrix}$ )的值, 就需要先知道Cov( $\begin{matrix} {\hat{M}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{M}}_{k} \end{matrix}$ )的值和Cov( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{R}}_{k} \end{matrix}$ )的值。其中Cov( $\begin{matrix} {\hat{M}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{M}}_{k} \end{matrix}$ )的值可以由观测数据得到。但是Cov( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{R}}_{k} \end{matrix}$ )的估计值需要进一步的探讨。因为不同维度的数据有相互独立的数据来源, 其所携带的噪音是相互独立的, 所以当j≠ k时, Cov( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{R}}_{k} \end{matrix}$ )=0; 当j=k时, Cov( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{R}}_{k} \end{matrix}$ )的值就是个方差, 可以用var( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ )来表示。

假定f_ij(· )的标准差为σ _ij。如此, [r_ij]第j维的值可以由对应的概率密度的方差的均值给出。因此, 可以估计var( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ )的值:

$\begin{matrix} var ({\hat{R}}_{j}) = \overset{N}{\sum_{i = 1}} σ_{ii}^{2} / N \end{matrix}$ （5）

在求var( $\begin{matrix} {\hat{R}}_{j} \end{matrix}$ )值的过程中要先求出不确定数据的概率密度, 这里将利用Matlab中的ksdensity函数求解:

$\begin{matrix} [f, x_{i}] = ksdensity (x) (6) \end{matrix}$

由式(6)计算样本向量X的概率密度估计, 返回在点x_i的概率密度f。再以每维数据为一个样本向量, 计算不确定数据各点的概率密度分布, 即f_ij(· )。式(5)所需要的标准差σ _ii的值可以由下式得到:

$\begin{matrix} σ_{ii} = \sqrt[]{\overset{N}{\sum_{j = 1}} {(f_{jj} (\cdot) - f_{ii} (\cdot))}^{2}} \end{matrix}$ （7）

根据上述过程得到Cov( $\begin{matrix} {\hat{S}}_{j} \end{matrix}$ , $\begin{matrix} {\hat{S}}_{k} \end{matrix}$ )的值, 它将被用于构造协方差矩阵[s_ij]或者称为C^S, 得到源数据真实的协方差结构。协方差矩阵[m_ij]和[s_ij]唯一的区别就在于后者的对角线上的值较低, 但是其他协方差值都是一样的。由于s_ij是由r_ij加上m_ij得到的, 所以协方差矩阵[s_ij]对角线上的值较低, 与我们的直觉相反。这是因为r_ij是被假定与不确定数据的真值相互独立的, 而不是与概率密度函数的平均估计值相互独立, 概率密度函数的平均估计值由于构造假定包含着被加入的噪音, 所以当我们知道[s_ij]是真实值, 不包含被加入的噪音, 而[m_ij]包含着不确定测量中的各种噪音时, 就可以很好地理解协方差矩阵[s_ij]对角线上的值较低的原因。

第二步, 利用获取到的数据真实的协方差结构, 进行数据的降噪处理。首先对协方差矩阵C^S进行对角化处理:

$\begin{matrix} C^{S} = V \cdot D \cdot V^{T} (8) \end{matrix}$

式中:矩阵D为相应的特征值; V为与特征值相对应的特征向量。

特征值越大代表着其对应的特征向量中包含的有效信息越多, 也就是背后其潜在的数据关联更为密切。在很多真实的数据集中, 特征值的结果大都趋近于0, 这也就是代表其对应的特征向量利用价值很少, 并且通常带有大量冗余和噪音, 对这样的信息进行聚类处理会对聚类结果造成很大的干扰并且降低效率。

将协方差矩阵D中元素按照从大到小方式进行排序, 即特征值由大到小排序, 并将对应的排序顺序保存在矩阵I中。然后将V中对应的特征向量按照I中特征值的顺序再进行排列。较大特征值对应的特征向量包含着数据的主要特性。采取按比例的方式, 保留相对来说较大的特征值以及对应的特征向量, 得到主要特征向量构成的投影矩阵。再利用投影矩阵将底层数据M转化成M', 此时M'就是经过处理锐化降噪后的数据, 此数据除去了大量的噪音, 有效地减少了不确定性。上述比例的选取要考虑到具体数据的维度以及数据间的相关程度, 需要在实验过程中有效地选取。

第三步, 利用K-means对锐化后的数据进行聚类分析。选择K-means算法是因为其对于噪声异常敏感, 并且在处理不确定数据时会对均值产生极大的影响, 这种传统的未经改进的聚类算法更能显示锐化降噪过程的有效性, 而改进过后的算法反而在某种程度上会影响对处理结果的判断。

综上, 基于谱分解的不确定数据聚类方法FD-means的详细流程, 如下所示。

算法1 FD-means

输入:

$\begin{matrix} {\bar{M}}_{1} \end{matrix}$ … $\begin{matrix} {\bar{M}}_{N} \end{matrix}$ :不确定观测数据的表示;

Proportion:降维比例;

k:簇的数量;

输出:k个簇的集合

方法:

构造观测数据 $\begin{matrix} {\bar{M}}_{1} \end{matrix}$ … $\begin{matrix} {\bar{M}}_{N} \end{matrix}$ 的协方差矩阵C^M;

根据Matlab函数ksdensity计算不确定数据对应的概率密度分布f_ij(· );

计算标准差σ _ii;

估计矩阵C^R其第j维对角线元素值为 $\begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix} \begin{matrix} σ_{ii}^{2} \end{matrix}$ /N, 其余元素为0;

获取源数据的真实协方差结构C^S=C^M-C^R;

利用公式C^S=V· D· V^T提取协方差矩阵C^S的特征值以及特征向量;

D=diag(D)将在对角线上的特征值提取放入矩阵D的第一维中;

[D, I]=sort(D, 'descend')将特征值按照降序进行排序;

in=floor(d· proportion)选取有效比例

N=V(:, I(1:in))按照特征值的顺序和选取比例, 排列特征向量, 得到投影矩阵;

M'=M· N对观测数据进行有效投影, 得到锐化后数据;

从M'中选取任意的k个对象作为初始簇中心;

Repeat

根据簇中对象的均值, 将每个对象分配到最相似的簇中;

重新计算每个簇中对象的均值, 更新簇均值;

until不再发生变化

3 实验及结果分析

本实验将对相同的不确定数据分别使用FD-means方法, K-means方法以及模糊K-means方法进行聚类。将其结果进行对比分析, 验证本方法的效果。

由于在大多数实际应用中可能无法获取数据的真实值, 而仅仅能够得到它们的不确定表示, 也就是观测数据。为了实验结果能够有一致的评判基准, 就需要人为地在UCI真实数据中加入噪音。把均值为0, 标准差在[0, 2f]范围内服从正态分布的噪音分别地加入到数据集的每个维度上。然后通过改变参数f的值, 就可以控制整个数据集的不确定性程度。显然, 各个维度f的选取都是带有随机性的, 所以整个数据集的不确定性是无法确定的。这里所加入的噪音就代表了在实际应用中因为数据收集或者构造产生的误差。

接下来, 从UCI数据库中选取了3个真实数据集, Poker Hand Training Data Set(PHT Data Set), 它包含了19 020条维度为11的数据; Abalone Data Set(Aba Data Set), 它包含4177条维度为8的数据; Breast Cancer Wisconsin(Original) Data Set(BCW Data Set), 它包含699条维度为10的数据。

本实验将选取两种重要的聚类评价指标, 它们分别为RMS均方根误差和CH指标。

RMS均方根误差:

$\begin{matrix} RMS = \frac{\sqrt[]{\overset{k}{\sum_{i = 1}} \sum_{x \in c_{i}} d (x, c_{i})^{2}}}{n} \end{matrix}$ （9）

式中:n为数据条目数; d(x, c_i) 为每一个数据点与它对应的聚类中心的距离。RMS的值越低, 代表聚类效果越好, 簇中对象越集中。并且RMS随着参数f变化的幅度越小, 代表聚类方法对于噪音的抵抗能力越强。

CH指标:

$\begin{matrix} CH = \frac{\frac{1}{k - 1} (\overset{k}{\sum_{i = 1}} n_{i} d^{2} (c_{i}, c))}{\frac{1}{n - k} (\overset{k}{\sum_{i = 1}} \sum_{x \subseteq c_{i}} d^{2} (x, c_{i}))} \end{matrix}$ （10）

式中:c为整个数据集的均值; c_i为第i簇的均值; k为分类数; n_i为第i簇内包含的对象个数; CH指标表示簇间距离与簇内距离的比值, CH值越高, 代表聚类效果越好。

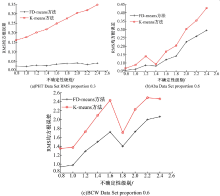
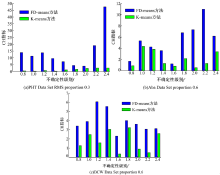
本文方法的源程序采用MATLAB2010a编写, 软件平台是Window7, 机器配置为i5(2.53 GHz), 2 GB RAM, 320 GB硬盘。实验结果如图1~图4所示。图1为FD-means与K-means的RMS均方根误差对比图, 图2为FD-means与K-means的CH指标对比图。由图1可以看出, 数据集PHT Data Set, Aba Data Set和BCW Data Set随着f的增加, FD-means方法的RMS均方根误差都低于K-means方法的RMS均方根误差, 并且受误差影响波动更微弱。由图2可以看出,

	Figure Option View Download New Window
	图1 RMS均方根误差基于FD-means与K-meansFig.1 RMS based on FD-means and K-means

	Figure Option View Download New Window
	图2 CH指标基于FD-means与K-meansFig.2 CH index based on FD-means and K-means

FD-means方法的聚类效果很大程度优于K-means方法, 因为CH值越高, 代表簇间距离比簇内距离比值越高, 聚类效果越好。

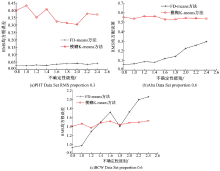
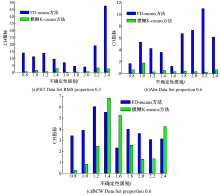
图3为FD-means与模糊K-means的RMS均方根误差对比图, 图4为FD-means与模糊K-means的CH指标对比图。由图3可以看出, 数据集PHT Data Set, Aba Data Set随着f的增加, FD-means方法的RMS均方根误差都低于模糊K-means方法的RMS均方根误差, 而数据集BCW Data Set随着f的增加出现了FD-means方法RMS均方根误差高于模糊K-means方法RMS均方根误差的情况, 这是因为数据集BCW Data Set规模很小, 其数据特征不明显, 不确定性难以进行清除造成的。而对于较大的数据集PHT Data Set, 可以看到, FD-means的聚类效果远远优于模糊K-means方法, 并且受误差影响波动也远弱于模糊K-means方法。由图4可以看出, FD-means方法的CH值远高于模糊K-means方法的CH值, 所以基于CH指标FD-means方法聚类效果同样很大程度优于模糊K-means方法。但是, 同样是在处理较小的数据集时可能会出现后者CH相近于前者CH, 或者高于前者CH的情况。这是因为不确定性的随机添加可能会导致某些原本不重要的属性对数据的影响加重, 干扰了算法的对象分配。而对于较小的数据集来说, 很难依据所给的少有的数据特征清除误差, 这就导致出现根据不重要的属性将对象分配的情况, 使CH指标相近于或者反而低于模糊K-means方法。

	Figure Option View Download New Window
	图3 RMS均方根误差基于FD-means与模糊K-meansFig.3 RMS based on FD-means and fuzzy K-means

	Figure Option View Download New Window
	图4 CH指标基于FD-means与模糊K-meansFig.4 CH index based on FD-means and fuzzy K-means

对比实验结果表明, 本文提出的FD-means方法更能够有效降低数据中的不确定性, 从本质上减少数据不确定性对聚类算法的影响, 使聚类结果受误差干扰程度减弱。本文方法有效地利用了不确定数据潜藏的内部关联结构, 最大程度地保留了不确定数据中的重要信息, 这样使经过锐化得到的降噪数据适用性更强, 可以应用于其他数据处理方法中。实验中所选取的数据集来源于医疗、科技等领域, 这些先期工作同样有助于相关领域的进一步研究, 挖掘相关数据的潜在价值。

最后, 针对FD-means算法的时间复杂度与传统算法以及改进算法的时间复杂度进行对比。传统算法K-means的时间复杂度为O(n), 即线性的, K-medoids改善K-means的噪音敏感后, 复杂度上升为O $\begin{matrix} (k {(n - k)}^{2}) \end{matrix}$ ; 传统DBSCAN算法的时间复杂度为O(n²), 基于DBSCAN的改进算法EXPDBSCAN的时间复杂度为O(s²· n²)。传统OPTICS算法的时间复杂度为O(n²), 其改进算法FOPTICS的时间复杂度也为O(s²· n²)。FD-means算法的时间复杂度的计算过程如下:首先需要计算FD-means方法的时间频度, 一个算法中语句执行次数称为语句频度或时间频度, 记为T(n)。FD-means方法中针对不确定数据进行锐化降噪过程的时间频度为T(n)=k²n²+mk²+ik, 其中n为数据量, k为数据维度, k、m、i均为常量。FD-means方法中锐化降噪过程的时间频度的计算方法如下:由算法1步骤可知, 求得C^M计算过程的时间频度是最为关键的, 算法利用了MATLAB中的Cov函数求解C^M, MATLAB中协方差矩阵的计算公式为:

$\begin{matrix} 协方差 (i, j) = (第 i 列所有元素 - 第 i 列均值) \times \frac{(第 j 列所有元素 - 第 j 列均值)}{(样本数 - 1)} \end{matrix}$ (11)

所以, 计算协方差矩阵的时间频度为k²n²+k²。而算法的其他步骤的时间频度可以统一概括成mk²+ik, 因为其都是与数据维度k相关的时间频度, 不涉及数据量n。由此, FD-means锐化降噪过程的时间频度为T(n)=k²n²+mk²+ik, 其时间复杂度为O(n²), 聚类过程K-means时间复杂度为O(n), 综上所述FD-means算法的时间复杂度为O(n²+n), FD-means算法的时间复杂度相较于传统算法, 其复杂度上升, 而与其他改进性算法的时间复杂度相近。

4 结束语

本文提出的FD-means方法以不确定数据本质特征为切入点, 根据不确定数据潜藏的内部协方差结构, 得到数据属性间的关联, 并利用这种关联最大程度地获取不确定数据中的主要信息, 该方法能够有效降低数据中的不确定性, 使聚类质量大幅提升。本文中得到的降噪数据适用性很强, 既可以使用多种聚类方法对其进行分析处理, 也可将其应用在信息分类、信息融合等其他数据处理领域, 具有非常广泛的应用空间。关于未来的工作, 将针对降噪处理过程再进行改进, 并与其他数据分析方法结合, 以达到更加显著的处理效果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	孟小峰, 慈祥. 大数据管理: 概念、技术与挑战[J]. 计算机研究与发展, 2013, 50(1): 146-169. Meng Xiao-feng, Ci Xiang. Big data management: concepts, techniques and challenges[J]. Journal of Computer Research and Development, 2013, 50(1): 146-169. [本文引用:1]
[2]	Aggarwal C C. On density based transforms for uncertain data mining[C]//Proceedings of the 23rd IEEE International Conference on Data Engineering. NJ: IEEE, 2007: 841-850. [本文引用:1]
[3]	Aggarwal C C. On unifying privacy and uncertain data models[C]//Proceedings of the 24th IEEE International Conference on Data Engineering. NJ: IEEE, 2008: 386-395. [本文引用:1]
[4]	Jin C, Yu J X, Zhou A, et al. Efficient clustering of uncertain data streams[J]. Knowledge and Information Systems, 2014, 40(3): 509-539. [本文引用:1]
[5]	Aggarwal C C, Yu P S. A survey of uncertain data algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2009, 21(5): 609-623. [本文引用:1]
[6]	Kriegel H P, Pfeifle M. Density-based clustering of uncertain data[C]//Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining. New York: ACM, 2005: 672-677. [本文引用:1]
[7]	张海龙, 王仁彪, 聂俊, 等. 海量数据的网格启发信息密度聚类算法[J]. 吉林大学学报: 工学版, 2011, 41(增刊2): 254-258. Zhang Hai-long, Wang Ren-biao, Nie Jun, et al. Grid heuristic information density clustering algorithm based on mass data[J]. Jounal of Jillin University(Engineering and Technology Edition), 2011, 41(Sup. 2): 254-258. [本文引用:1]
[8]	Kriegel H P, Pfeifle M. Hierarchical density based clustering of uncertain data[C]//Proceedings of the 5th IEEE International Conference on Data Mining. NJ: IEEE, 2005: 689-692. [本文引用:1]
[9]	Ngai W K, Kao B, Chui C K, et al. Efficient clustering of uncertain data[C]//Proceedings of the 6th IEEE Internatiaonal Conference on Data Mining. NJ: IEEE, 2006: 436-445. [本文引用:1]
[10]	Lee S D, Kao Ben, Cheng Reynold. Reducing UK-means to K-means[C]//IEEE 13th International Conference on Data Mining Workshops, Omaha, Nebraska, USA, 2007: 483-488. [本文引用:1]
[11]	李云飞, 王丽珍, 周丽华. 不确定数据的高效聚类方法[D]. 广西师范大学学报: 自然科学版, 2011, 29(2): 21-27. Li Yun-fei, Wang Li-zhen, Zhou Li-hua. Efficient clustering algorithm of uncertain data[D]. Journal of Guangxi Normal University (Natural Science Edition), 2011, 29(2): 21-27. [本文引用:1]
[12]	Aggarwal C C. A framework for clustering uncertain data streams[C]//Proceedings of the 24th IEEE International Conference on Data Engineering. NJ: IEEE, 2008: 150-159. [本文引用:1]
[13]	Aggarwal C C. On high dimensioal projected clustering of uncertain data streams[C]//Proceedings of 25th International Conference on Data Engineering. NJ: IEEE, 2009: 1152-1154. [本文引用:1]
[14]	曹振丽, 孙瑞志, 李勐. 一种基于高斯混合模型的不确定数据流聚类方法[J]. 计算机研究与发展, 2014, 51(增刊2): 102-109. Cao Zhen-li, Sun Rui-zhi, Li Meng. A method for clustering uncertain data streams based on GMM[J]. Journal of Computer Research and Development, 2014, 51(Sup. 2): 102-109. [本文引用:1]
[15]	Aggarwal C C. On multidimensional sharpening of uncertain data[C]//Proceedings of the SIAM International Conference on Data Mining. PA: SIAM, 2010: 136-148. [本文引用:1]

2013

0.0

. 2013, 50(1):146-169

Big data management:concepts,techniques and challenges

大数据管理:概念、技术与挑战

Meng Xiao-feng , Ci Xiang.

孟小峰, 慈祥

... 0 引言随着各种新型信息发布方式的不断涌现,以及云计算、物联网等技术的快速发展,数据正以前所未有的速度在不断地增长和积累,大数据时代已经到来^[1] ...

2007

0.0

... 数据的不确定性来源于多种情况,物理仪器采集数据所产生的误差,环境状况对数据的影响,网络传输中受到带宽、传输延时等因素的干扰^[2],以及出于隐私保护的目的等都可能导致数据不确定性的产生^[3] ...

2008

0.0

2014

0.0

... 数据不确定性的表现形式分为两种,即存在级的不确定性和属性级的不确定性^[4] ...

2009

0.0

... 存在级不确定性代表元组的不确定性,属性级不确定性代表元组数据值的不确定性,数据挖掘领域多考虑的是属性级的不确定性^[5] ...

2005

0.0

... Kriegel等^[6]通过改进DBSCAN算法^[7]提出了基于密度的不确定数据聚类算法FDBSCAN,并且改进了OPTICS算法,提出了FOPTICS算法^[8] ...

2011

0.0

. 2011, 41(增刊2):254-258

Grid heuristic information density clustering algorithm based on mass data

海量数据的网格启发信息密度聚类算法

Zhang Hai-long , Wang Ren-biao , Nie Jun

张海龙, 王仁彪, 聂俊

... Kriegel等^[6]通过改进DBSCAN算法^[7]提出了基于密度的不确定数据聚类算法FDBSCAN,并且改进了OPTICS算法,提出了FOPTICS算法^[8] ...

2005

0.0

... Kriegel等^[6]通过改进DBSCAN算法^[7]提出了基于密度的不确定数据聚类算法FDBSCAN,并且改进了OPTICS算法,提出了FOPTICS算法^[8] ...

2006

0.0

... Ngai等^[9]提出了利用MBR最小边界矩形以及剪枝策略的UK-means算法 ...

2007

0.0

... Lee等^[10]在UK-means的基础之上,提出了计算量大幅降低的CK-means算法 ...

2011

0.0

... 而后李云飞等^[11]根据CK-means再次提出改进,简化距离计算,提高算法效率 ...

2008

0.0

... 除此之外,不确定数据的研究也扩大到不确定数据流的方向上,Aggarwal等^[12]提出了扩展CF结构的UMicro算法,并针对高维不确定数据流提出了投影聚类方法,解决了高维数据聚类所面临的一定问题^[13] ...

2009

0.0

2014

0.0

. 2014, 51(增刊2):102-109

A method for clustering uncertain data streams based on GMM

一种基于高斯混合模型的不确定数据流聚类方法

Cao Zhen-li , Sun Rui-zhi , Li Meng.

曹振丽, 孙瑞志, 李勐

... 曹振丽等^[14]也提出一种基于高斯混合模型的不确定数据流聚类方法 ...

2010

0.0

... 2 FD-means聚类方法第一步,获取不确定数据的真实协方差结构,Aggarwal在多维锐化不确定数据表示的文章中提出了一种方法可以用于获取所需的协方差结构^[15],本文将引用这种方法 ...