BB84协议是第一个量子密钥分配协议^[2]。协议包含4个偏振态和两组正交基。主要工作流程如下:发送方Alice制备并发送单光子序列, 每个光子随机选取一种偏振态; 接收方Bob随机选取+基和× 基测量光子偏振态并记录光子位置信息; 通过经典信道Bob将测量基发送给Alice, 双方进行基矢比对, 保留相同的测量基; 最后, Alice和Bob将保留的光子偏振态信息转换成相应的密钥比特信息, 经过纠错和私密放大得到最终的安全通信密钥。

目前, 量子密钥分发系统中并不存在完美的单光子源, 因此通信双方实际使用的是衰减后的相干光, 以及压缩光等亚泊松分布光源。假设光源相位完全随机, p_n表示发送脉冲中出现n光子态的概率, μ 表示相干光的平均光子数, 光源表达式为:

ρ _A= ∑n=0∞p_n|n> < n|= ∑n=0∞e^-μ μnn!|n> < n| (1)

采用强衰减方法得到的弱相干脉冲传输过程中易受环境影响, 导致信号衰减。实验使用的1550 nm的商用单模光纤衰减系数α 为0.20 dB/km, l代表信道长度, 信号脉冲在信道中的传输效率可表示为:

tAB=10-αl/102

实际通讯过程中, 探测器及其他光学设备中也包含一些固有损耗, 以t_Bob表示探测器的探测效率, η _D表示在光学设备固有损耗下的传输效率, 则单光子在实际QKD系统中的总传输效率η 可表示为:

η=tABtBobηD3

由式(3)可得, n光子脉冲的总传输效率(假设多光子脉冲中的光子均为独立传输)为:

η _n=1- 1-ηn=1- 1-tABtBobηDn(4)

Bob探测到Alice发出n个光子的脉冲概率可表示为:

Yn=Y0+ηn-Y0ηn≈Y0+ηn5

光源的总计数率为:

Qμ=∑n=0∞Qμ=∑n=0∞pnYn6

结合式(4)(5)可得, n光子态的量子比特错误率(Quantum bits error rate, QBER)为:

en=e0Y0+edetηnYn(7)

式中:e_det为单光子错误到达探测器的概率; 假设背景噪音完全随机进而引起的错误也完全随机, 即e₀=1/2。

由式(1)(5)(6)(7)可得系统总QBER:

EμQμ=∑n=0∞enYnpn（8）

式中:Q_μ 为探测效率; E_μ 为总误码率。

用δ 表示原始密钥误码率, H₂(δ )表示纠错泄露的信息量, 则在理想单光子光源状态下QKD系统安全成码率可表示为:

R=1-H2δ-H2δp(9)

但是, 实际系统中会存在某些漏洞, GLLP公式给出了常用的弱相干光源BB84协议安全密钥率, 可以写成如下的形式^[16]:

R≥q-fEμQμH2Eμ+Q11-H2e110

式中:q为对基效率; f(E_μ )为纠错效率。

本文采用的诱骗态方法中包含信号态、诱骗态、真空态3种不同平均光子数的脉冲。发射几率分别为p_μ 、p_v、p₀, Y_k表示k光子在接收端被探测到的几率, 则信号态和诱骗态误码率可分别表示为:

E_μ = 1Que0p0, μY0+e1p1, μY1+∑k=2∞ekpk, μYk

E_v= 1Qμe0p0, vY0+e1p1, vY1+∑k=2∞ekpk, vYk

结合式(10)可以得到诱骗态方法安全码率的下限^[11]。

基于BB84协议原理, 本文设计并搭建了Alice到Bob的点对点量子密钥分发及量子信道应力分析整合实验系统, 系统主要部件和结构如图1所示。QKD系统工作频率为40 MHz, 信号光脉宽为200 ps。双方通过量子信道实现密钥分发, 通过经典信道实现基矢比对和数据传输。应力测试装置对量子信道实施外力作用, 应力分析系统采集信道应力变化相关数据和量子密钥分发相关数据信息。在整个应力分析实验中, 本文采用长度为20 m、内径为9 μ m、外径为125 μ m、波长为1550 nm的商用单模光纤作为量子信道, 信道衰减为0.2 dB。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 点对点量子保密通信应力分析系统Fig.1 Point to point quantum cryptography stress analysis system

(1)压力作用下量子密钥分发误码率及成码率分析

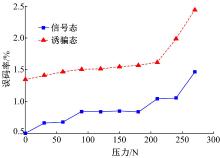
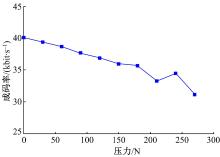
量子信道对外力作用十分敏感, 为了保持系统稳定, 经多次验证, 本文将压力的位移速度设定为3.6 mm/s, 垂直下压光纤, 光纤受力长度为30 cm。压力F_pre从0 N开始, 每次增加30 N, 约30 s作用力稳定后, 采集数据。经计算后得到信号态误码率、诱骗态误码率以及成码率随压力的变化曲线, 如图2、图3所示。从图2可以看出, 随着压力的增加, 无论是信号态错误率还是诱骗态错误率都随之增大。这与文献[15]通过POVM半正定算子测量方法仿真得出的理论结果相符。另外, 相同压力作用下, 诱骗态的错误率要明显高于信号态错误率。但是, 当压力增加到300 N时, 超出信道承载极限, 量子密钥分发系统会进行偏振反馈, 重新建立连接。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 压力作用下误码率曲线Fig.2 Bit error rate curve under pressure

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 压力作用下成码率曲线Fig.3 Bit generation rate curve under pressure

图3中数据点纵坐标为系统30 s内成码率均值。可以看出, 随着压力的增大, 系统成码率呈下降趋势。值得注意的是, 当压力小于180 N时下降趋势比较稳定, 而当压力大于210 N时震荡较为明显, 此阶段诱骗态错误率上升趋势极为明显, 迅速逼近误码率极限。可见, 量子信道在小于210 N压力作用下, 量子密钥分发过程是相对稳定的。

(2)拉力作用下量子密钥分发误码率及成码率分析

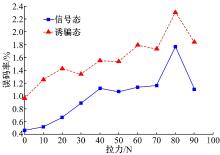
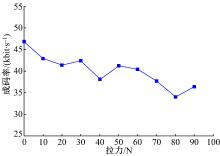
将拉力的位移速度设定为2.5 mm/s, 沿光纤轴向进行拉伸实验。拉力F_ten从0 N开始, 每次增加10 N, 系统稳定后采集数据。信号态误码率、诱骗态误码率以及成码率随拉力的变化曲线如图4、图5所示。从图4可以看出, 随着拉力的增加, 信号态错误率和诱骗态错误率都相应增大, 总体呈现震荡上升趋势。相同拉力作用下, 信号态错误率低于诱骗态的错误率。值的注意的是, 当拉力大于70 N时, 错误率急速上升后又转而下降, 呈现不稳定状态, 超过90 N时量子密钥分配发生错误。另外, 随着拉力的增加, 系统成码率呈震荡下降趋势, 如图5所示。相对于压力作用, 拉力对误码率和成码率的影响更为明显。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 拉力作用下误码率曲线Fig.4 Bit error rate curve under tension

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 压力作用下成码率曲线Fig.5 Bit generation rate curve under tension

另外, 本文采集了拉力变化下光纤量子信道的衰减数据, 与相同作用力下的信号态误码率、诱骗态误码率进行对比, 如表1所示。可以看出, 随着衰减的增加, 误码率也相应增大。当衰减大于4.85 dB后, QKD系统无法正常生成密钥。

综合以上分析可以推断, 应力导致光纤信道衰减发生变化, 进而使QKD系统误码率增加, 最终影响密钥的生成。

表1

Table 1

表1(Table 1)

表1 衰减与误码率的关系 Table 1 Relationship of attenuation and bit error rate 拉力/N 10 20 30 40 50 60 70 80 90 信道衰减/dB 0.22 0.33 0.57 0.82 1.69 2.17 3.71 4.25 4.85 信号态误码率/% 0.52 0.66 0.88 1.12 1.06 1.13 1.16 1.77 1.10 诱骗态误码率/% 1.25 1.42 1.34 1.55 1.53 1.79 1.73 2.30 1.84

表1 衰减与误码率的关系 Table 1 Relationship of attenuation and bit error rate