一种高灵敏度Galileo E1B/C联合捕获方法

引用本文

罗士栋, 巴晓辉, 王云, 陈杰. 一种高灵敏度Galileo E1B/C联合捕获方法. 吉林大学学报（工学版）, 2017, 47(5): 1617-1624
LUO Shi-dong, BA Xiao-hui, WANG Yun, CHEN Jie. Joint strategy for high sensitivity Galileo E1B/C signal acquisition. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1617-1624 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705039
Permissions

一种高灵敏度Galileo E1B/C联合捕获方法

罗士栋^1,², 巴晓辉¹, 王云¹, 陈杰¹

1.中国科学院微电子研究所,北京 100029

2.中国科学院大学,北京 100049

通信作者:陈杰(1963-),男,研究员,博士生导师.研究方向:通信,多媒体处理,VLSI设计.E-mail:jchen@ime.ac.cn

作者简介:罗士栋(1984-),男,助理研究员,博士研究生.研究方向:超大规模集成电路设计.E-mail:luoshidong@ime.ac.cn

基金项目:国家自然科学基金项目(61376027)

摘要

提出了一种基于中频回放的Galileo E1B/C联合捕获架构,该架构可以时分复用处理E1B/C信号,之后将处理结果联合起来进行判决,相比只使用E1B或E1C信号有更高的发现概率,且不增加硬件规模。同时,本文提出了一种门限结合码相位判决方法,该方法利用门限以及中频数据不同起始点多次回放间卫星信号码片相关性,弱星发现概率相比传统恒虚警率门限判决方法有较大的提高,在系统虚警率为0.002, 载噪比低至27 dB·Hz情况下,捕获轮数为2,每轮取前10个最大值,门限结合码相位判决方法发现概率接近40%,而此时传统恒虚警率门限判决方法发现概率不足10%。

关键词: 通信技术; Galileo E1信号捕获; 中频回放; 门限结合码相位; 高灵敏度

中图分类号:TN967.1 文献标志码:A 文章编号:1671-5497(2017)05-1617-08

Joint strategy for high sensitivity Galileo E1B/C signal acquisition

LUO Shi-dong^1,², BA Xiao-hui¹, WANG Yun¹, CHEN Jie¹

1.Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100029, China

2.University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

High sensitivity acquisition architecture for Galileo E1 signal is proposed. This architecture processes E1B/C signals by time-division multiplexing, and then joins the results together. Compared with individual E1B or E1C channel acquisition, higher detection probability is achieved without the increase in hardware burden. In addition, a novel decision strategy, named threshold combining code phase, is also proposed. The strategy utilizes threshold and the code phase correlation of correct cell between multiple Intermediate Frequency (IF) data replays with different starting point of each replay. Compared with traditional threshold decision strategy based constant false alarm rate, the proposed strategy enhances the detection probability. When overall false probability is 0.002 and Carrier to Noise Ratio (CNR) downs to 27 dBHz, the number of acquisition rounds is 2, and the top 10 maximum values are retained in each round, the overall detection probability of the decision strategy is near 40%, while the overall detection probability of the traditional threshold decision strategy is less than 10%.

Key words: communication technology; Galileo E1 signal acquisition; IF signal replay; threshold combines with code phase; high sensitivity

Show Figures

0 引言

Galileo凭借其更优越的星座结构和信号体制特点, 使其在定位精度、抗多径性能、完好性监测等方面都优于GPS系统。Galileo信号捕获为近年来研究热点。

文献[1-3]提出了联合利用Galileo E1导频/数据通道结构的捕获策略用于提高接收机灵敏度。文献[4]的仿真表明双边带捕获相比单边带捕获性能改善大约2 dB。本文使用双边带以及导频/数据通道联合捕获以提高捕获灵敏度。另外, 为了进一步提高发现概率, 文献[5-10]介绍了一些相关器相关之后的处理技术:相干、非相干、差分。文献[5, 6]通过延长相干积分时间来提高增益, 然而由于未知的数据以及二级码跳变存在, 这需要辅助信息进行辅助。文献[7]提出了一种非相干联合技术, 这种技术将一些包络函数相加, 带来平方损失。文献[8-10]介绍了差分联合技术, 这种技术中相关器输出与它的延迟的共轭相乘, 但是由于Galileo E1信号数据比特长度与码周期一致, 这将带来6 dB^[8]损失。考虑到独立Galileo接收机复杂度与灵敏度, 本文采用非相干技术用于相关器相关之后的处理。

文献[11]提出了一种二维压缩相关器快速捕获Galileo E1信号方法, 这种方法第一阶段利用一个二维压缩相关器进行相关捕获, 第二阶段使用常规相关器搜索第一阶段捕获到的几个伪码相位以及多普勒频偏。这种方法在第一阶段使用压缩方案使得发现概率有所降低, 压缩并行度越高, 发现概率降低越多, 但是能够明显提高捕获速度。本文提出的捕获引擎系统结构通过中频RAM存储信号可以让系统以高于中频采样率的频率对信号进行处理, 提高系统捕获速度, 同时本文在捕获判决时使用门限结合码相位判决的方法提高发现概率。本文提出的捕获以及判决方法是一种通用的方法, 可以灵活应用到其他导航系统中。

1 中频回放式E1B/C联合捕获架构

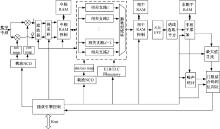
图1为本文设计的E1B/C联合捕获引擎的系统结构图。对于E1信号来说, 该结构为时分复用, 先处理E1B(数据通道)上边带信号, 之后处理E1B下边带信号。E1C(导频通道)信号处理过程与E1B类似, 最后将4个边带非相干结果累加联合起来进行判决。

捕获引擎的工作流程可简要描述为:

(1)数字中频信号首先下变频至基带, 经低通滤波器后降采样至半码片速率附近, 存储基带信号至本地的中频RAM中。

(2)存储结束后, 高速回放中频RAM中数据至相关器阵列, 记录中频回放起始时间, 短时相关结果存储至相干RAM中作缓存。

	Figure Option View Download New Window
	图1 捕获引擎系统结构图Fig.1 Acuqisition engine structure

(3)相干积分结束后, 输出短时相关结果至快速傅里叶变换(Fast Fourier transform, FFT)单元, FFT运算输出后选择一半谱线, 平方后得到能量值。

(4)能量值与非相干RAM中存储的对应值输出至非相干累加单元, 实现累加, 累加结束后将相应的结果存回非相干RAM。

(5)非相干累加结束后, 搜索前K个最大值以及统计噪底, 输出前K个最大值及其对应码片频偏、噪底、回放起始时间至捕获引擎控制模块。

(6)处理器通过总线取回这些结果, 并在处理器作软件判决, 根据判决结果配置下一次捕获参数。

2 Galileo E1B/C信号捕获分析

接收机接收Galileo E1B/C信号经过射频变频滤波后, 再经过ADC(Analog-to-digital converter)变为数字中频信号。文献[12]证明了对于捕获来说, BOC(1, 1)(Binary Offset Carrier)与CBOC(6, 1, 1/11)(Composite-binary offset carrier)性能差距可以忽略, 因此对于某一颗卫星来说, 忽略BOC(6, 1)信号, k时刻数字中频信号表达式如下:

$\begin{matrix} \begin{matrix} y (k) = A [d (k) c_{d} (k) - p (k) c_{p} (k)] \\ \cos [2 πk T_{s} (f_{IF} + f_{dop}) + φ_{0}] \\ sgn [\sin (2 πk T_{s} f_{sc})] \approx \\ A [d (k) c_{d} (k) - p (k) c_{p} (k)] \\ \cos [2 πk T_{s} (f_{IF} + f_{dop}) + φ_{0}] \\ \sin (2 πk T_{s} f_{sc}) = \\ \frac{A}{2} B (k) {\sin [2 πk T_{s} (f_{sc} + f_{c}) + φ_{0}] + \\ \sin [2 πk T_{s} (f_{sc} - f_{c}) - φ_{0}]} + η_{0} (k) \end{matrix} \end{matrix}$ （1）

式中:B(k)=d(k)c_d(k)-p(k)c_p(k), d(k)为k时刻数据通道导航电文比特, p(k)为导频通道二次码, c_d(k)和c_p(k)分别为k时刻数据通道以及导频通道码序列值; f_c=f_IF+f_dop, f_IF和f_dop分别为中频载波频率和多普勒频偏; A为接收机接收信号幅度; f_sc为子载波频率; T_s为采样周期; φ ₀为载波初相; η ₀(k)为中心频率位于f_IF高斯白噪声, 其均值为0, 方差为σ ²。

在本文中, 相干积分总时间设为T_Coh, 短时相关分段数为M, 则短时积分时间为T_p=T_Coh/M, 短时相关时间内采样点数L=T_p/T_s。

2.1 捕获过程公式推导

首先对数据通道进行上边带捕获推导, 在第i个总相干积分时间T_Coh内, 第n段短时相关中, 数据通道短时相关输出信号项可表示为:

$\begin{matrix} \begin{matrix} I_{i, s, dup} (n) + j Q_{i, s, dup} (n) = \frac{A}{4} d (k) R_{d} (τ_{id}) \cdot \\ \frac{\sin (πLΔf T_{s})}{\sin (πΔf T_{s})} [\cos (Δφ'_{i}) + jsin (Δφ'_{i})] \end{matrix} \end{matrix}$ (2)

式中:τ _i_d为k时刻接收中频信号中数据通道伪码与本地复现数据通道伪码的相位延迟; Δ φ '_i=Δ φ +π (2Ln+L-1)Δ fT_s, Δ f和Δ φ 分别为接收信号载波与本地复现载波之间的残留频差和残相差; R_d(τ _i_d)为数据通道伪码自相关函数。短时相关输出I路噪声和Q路噪声仍服从高斯分布, 其均值为零, 方差为Lσ ²/2。

对短时相关输出的M个值作N点复数FFT运算, 假定在推导过程中, τ _i_d保持不变, 并且假定电文比特不发生翻转, 即d(k)维持不变, 则N点复数FFT运算后信号项为:

$\begin{matrix} \begin{matrix} I'_{i, s, dup} (m) + jQ'_{i, s, dup} (m) = \\ [\cos (ψ_{1}) + jsin (ψ_{1})] \frac{A}{4} d (k) R_{d} (τ_{id}) \cdot \\ \frac{\sin (πLΔf T_{s})}{\sin (πΔf T_{s})} \frac{\sin [πM (Δ f T_{p} - m / N)]}{\sin [π (Δf T_{p} - m / N)]} \end{matrix} \end{matrix}$ （3）

FFT运算后I路噪声与Q路噪声仍为高斯分布, 其均值为0, 方差为LMσ ²/2。

类似地, 对数据通道进行下边带捕获, 得到相应的复数FFT运算后信号项为:

$\begin{matrix} \begin{matrix} I'_{i, s, ddown} (m) + jQ'_{i, s, ddown} (m) = \\ [\cos (ψ_{2}) + jsin (ψ_{2})] \frac{A}{4} d (k) R_{d} (τ_{id}) \cdot \\ \frac{\sin (πLΔf T_{s})}{\sin (πΔf T_{s})} \frac{\sin [πM (Δ f T_{p} - m / N)]}{\sin [π (Δf T_{p} - m / N)]} \end{matrix} \end{matrix}$ （4）

同理, 对导频通道进行上/下边带捕获, 可得FFT运算后信号项结果。

设非相干累加次数为P, 且在整个非相干累加操作内接收中频信号中数据(导频)通道伪码与本地复现数据通道伪码的相位延迟τ _i_d(τ _i_p)维持不变。联合使用E1B/C信号捕获, 非相干累加之后信号项可表示为:

$\begin{matrix} \begin{matrix} Y_{s} (m) = \frac{A^{2}}{8} P [R_{d}^{2} (τ_{id}) + R_{p}^{2} (τ_{ip})] \cdot \\ {\{\frac{\sin (πLΔf T_{s})}{\sin (πΔf T_{s})} \frac{\sin [πM (Δ f T_{p} - m / N)]}{\sin [π (Δf T_{p} - m / N)]}\}}^{2} \end{matrix} \end{matrix}$ （5）

此时噪声项服从自由度为8P的中心χ ²分布, 其均值为8PLMσ ²/2, 方差为16P· [LMσ ²/2]²。

信号项加噪声项服从自由度为8P的非中心χ ²分布, 均值为:

$\begin{matrix} \begin{matrix} s_{1} = 4 PLM σ^{2} + \frac{A^{2}}{8} P [R_{d}^{2} (τ_{id}) + R_{p}^{2} (τ_{ip})] \cdot \\ {\{\frac{\sin (πLΔf T_{s})}{\sin (πΔf T_{s})} \frac{\sin [πM (Δ f T_{p} - m / N)]}{\sin [π (Δf T_{p} - m / N)]}\}}^{2} \end{matrix} \end{matrix}$ （6）

方差为:

$\begin{matrix} \begin{matrix} {δ_{1}}^{2} = 4 P [LM σ^{2}]^{2} + \\ \frac{A^{2}}{4} LM σ^{2} P [R_{d}^{2} (τ_{id}) + R_{p}^{2} (τ_{ip})] \cdot \\ {\{\frac{\sin (πLΔf T_{s})}{\sin (πΔf T_{s})} \frac{\sin [πM (Δ f T_{p} - m / N)]}{\sin [π (Δf T_{p} - m / N)]}\}}^{2} \end{matrix} \end{matrix}$ （7）

若只使用E1B或E1C信号捕获, 则非相干累加之后信号项加噪声项服从自由度为4P的非中心χ ²分布。

2.2 门限判决方法分析

采用文献[13]中给出的基于恒虚警率的门限设计算法, 得到E1B/C双边带联合捕获判决门限为:

$\begin{matrix} V_{t} = \sqrt[]{4 P} LM σ^{2} Q^{- 1} (P_{fa}) + 4 PLM σ^{2} (8) \end{matrix}$

发现概率为:

$\begin{matrix} P_{d} = Q (\frac{V_{t} - s_{1}}{δ_{1}}) \end{matrix}$ (9)

式中:Q(x)= $\begin{matrix} \frac{1}{\sqrt[]{2 π}} \end{matrix} \begin{matrix} \int_{x}^{\infty} \end{matrix} \begin{matrix} e^{- t^{2} / 2} \end{matrix}$ dt。

2.3 门限结合码相位判决方法分析

门限结合码相位判决方法具体过程如下:从第一轮捕获开始, 每轮首先使用门限进行判决, 若超过门限则捕获成功, 停止捕获; 若不超过门限, 则记录前K个最大值对应的多普勒频偏以及伪码相位, 捕获轮数加1, 继续下一轮捕获。若J轮捕获门限判决都失败, 则根据J轮记录的每轮前K个最大值对应的多普勒频偏以及伪码相位做进一步判决。相比唐搜索检测器以及N中取M的搜索检测器, 该方法不是仅仅判决统计量峰值, 而是保留更多的候选观测量, 通过后续的比较和统计得出判决结果。

2.3.1 门限结合码相位判决方法具体流程

对同一颗星, 捕获J轮, 每轮捕获对应的中频回放起始时间为T(i)(i=1, 2, …, J)。每轮捕获的判决量表示为R(τ , f_d), τ 和f_d分别为捕获结果的伪码相位和多普勒频率, 取R(τ , f_d)的前K个最大值:

$\begin{matrix} RR (τ, f_{d}) = \max (R (τ, f_{d}), K) \end{matrix}$ （10）

式中:max(X, K)表示取X的前K个最大值; 每轮捕获记录RR(τ , f_d)对应的多普勒频率和伪码相位, J轮捕获完成后得到多普勒频率矩阵F_{J* K}、伪码相位矩阵C_{J* K}。

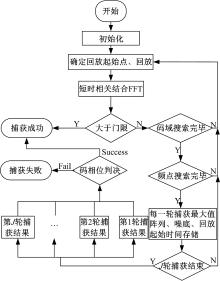
	Figure Option View Download New Window
	图2 门限结合码相位判决流程图Fig.2 Flow chart of threshold combines code phase decision strategy

图2为门限结合码相位判决流程图, 具体步骤如下:

第一步若RR(τ , f_d)中最大值超过基于恒虚警率门限判决方法确定的门限, 则判定捕获成功, 否则进入第二步。

第二步以F_{J* K}中第一个值为比较对象, 记为F(m₀, n₀)。按式(11)确定伪码相位比较集合V, 其中C(i, j)表示矩阵C_{J* K}中对应第i行第j列的值。

$\begin{matrix} \begin{matrix} (i, j) = \{(i, j) || F (i, j) - F (m_{0}, n_{0}) | < f_{th}\} \\ i \in (1, J), i \neq m_{0}, j \in (1, K), V = \{C (i, j)\} \end{matrix} \end{matrix}$ （11）

式中:f_th为预先设定的多普勒偏移门限。

第三步取F(m₀, n₀)对应的码相位记为C(i₀, j₀), 与V中值一一比较, 现以第二个值C(i₁, j₁)为例分析比较过程。C(i₀, j₀)、C(i₁, j₁)对应的中频回放起始时间分别为T(i₀)、T(i₁)。T(i₀)至T(i₁)时间间隔内卫星走过的理论半码片数为:

$Δc'_{w} = (f_{code} + F (m_{0}, n_{0}) f_{code} / f_{L 1}) \cdot (T (i_{1}) - T (i_{0}))$ （12）

式中:f_code表示半码片速率, 其值为2.046 MHz, f_L1为1575.42 MHz。

第四步计算T(i₁)时刻的理论伪码相位为:

$\begin{matrix} C' (i, j) = (Δc'_{w} + C (i_{0}, j_{0} {))}_{S} (13) \end{matrix}$

式中:S为Galileo E1信号半码片数, 其值为8184, (x)_S表示x对S的取模操作。

第五步判决。如果|C(i₁-j₁)-C'(i, j)|≤ th, th为预先设定的码片偏移门限, 则判定捕获成功; 否则, 重复第二至第五步完成V中所有值与C(i₀, j₀)比较, 若V中所有值都比较完, 均捕获不成功, 则回归第二步, 取F_{J* K}中下一个频率值为比较对象, 记为F(m₀, n₀), 重复上述比较过程。若F_{J* K}中所有值比较完, 均捕获失败, 则判定整个捕获过程失败。

2.3.2 多轮捕获多普勒以及码片偏移门限设计

码片对齐时, 当频率分辨率比较小时, 非相干累加后的统计量会在正确谱线以及相邻谱线出现较大值, 以谱线分辨率为172 Hz为例(1 ms分11段时), f_th可设为200, 表示相邻两根谱线从属同一频率范围。

码片偏移门限th的设定由采样率偏差决定。假设标称采样率为f_s, 实际采样率为f'_s, 则标称1 s的时间实际为f_s/f'_s。标称t秒内, 走过的半码片数为(f_code+F(m₀, n₀)f_code/f_L1)t, 实际走过的半码片数为(f_code+F(m₀, n₀)f_code/f_L₁)tf_s/f'_s, 这样, 产生的半码片偏差为(f_code+F(m₀, n₀)f_code/f_L₁)t(f_s-f'_s)/f'_s。由于F(m₀, n₀)f_code/f_L₁这一项要远远小于f_code, 这样半码片偏差约为f_codet(f_s-f'_s)/f'_s, 若标称采样率f_s为16 368 000 Hz, 实际采样率f'_s为16 367 996 Hz, 以两次捕获间隔t=1 s为例, 则产生的半码片偏差为0.5, 这样th可设为1。

2.4 系统发现概率与虚警率分析

为了叙述方便, 记事件一为单轮RR(τ , f_d)最大值包含卫星信号能量且超过基于门限判决方法确定的门限; 事件二为单轮RR(τ , f_d)最大值为噪声能量且超过基于门限判决方法确定的门限; 事件三为单轮RR(τ , f_d)里某个值包含卫星信号能量并且没有超过基于门限判决方法确定的门限; 事件四为单轮RR(τ , f_d)都为噪声能量并且没有超过基于门限判决方法确定的门限。

2.4.1 系统发现概率分析

当卫星信号存在时, 门限结合码相位判决方法发现卫星信号由以下两部分组成:

(1)第j(1≤ j≤ J)轮捕获发生事件一, 并且小于j的轮数里没有发生事件一。

(2)j(2≤ j≤ J)轮捕获中有两轮及以上发生事件三, 并且这两轮卫星信号对应的多普勒频率以及伪码相位飘移在设定门限以内。

第一部分中每轮捕获的发现概率可由式(9)获得, 因此第一部分发现概率为:

$\begin{matrix} P_{d 1} = P_{d} + (1 - P_{d}) P_{d} + \dots + (1 - P_{d})^{J - 1} P_{d} (14) \end{matrix}$

捕获J轮, 每轮都用门限判决方法, 其发现概率即为上述第一部分。

对于第二部分发现概率, 根据文献[14], 对于每轮捕获, 信号能量位于前K个最大值的概率为:

$\begin{matrix} P_{K} = \int_{0}^{\infty} \overset{K - 1}{\sum_{n = 0}} C_{U - 1}^{n} [1- F {(x)]}^{n} [F {(x)]}^{U - 1 - n} \cdot p (x |H_{1}) dx \end{matrix}$ (15)

式中:F(x)= $\begin{matrix} \int_{0}^{x} \end{matrix}$ p(y $\begin{matrix} |H_{0} \end{matrix}$ )dy; U为搜索的单元数; p(x $\begin{matrix} |H_{0} \end{matrix}$ )、p(x $\begin{matrix} |H_{1} \end{matrix}$ )分别为没有卫星信号以及有卫星信号情况下捕获判决量的概率密度函数。

假定多普勒频率以及伪码相位飘移门限设定合理, 使得捕获时间里飘移在设定门限以内, 那么第二部分发现概率为:

$\begin{matrix} P_{d 2} = \overset{J}{\underset{z = 2}{\sum C_{J}^{z}}} (1 - P_{d})^{J} (1 - P_{K})^{J - z} (P_{K})^{z} \end{matrix}$ (16)

由于第一与第二部分为互斥事件, 因此系统发现概率为P_ds=P_d1+P_d2。

2.4.2 系统虚警率分析

门限结合码相位判决方法系统虚警率由以下两部分组成:

(1)J轮捕获中第j(1≤ j≤ J)轮RR(τ , f_d)发生事件二, 并且小于j的轮数里没有发生事件二。

(2)j(2≤ j≤ J)轮捕获中有两轮及以上发生事件四, 并且这两轮噪声对应的多普勒频率以及伪码相位飘移在设定门限以内。

对于并行捕获, 由文献[15]可知, 单轮捕获系统虚警率为:

$\begin{matrix} P_{FA} = 1 - (1 - P_{fa})^{U} \end{matrix}$ （17）

式中:P_fa为搜索单个单元格的虚警率。

第一部分虚警率为:

$\begin{matrix} P_{fa 1} = P_{FA} + (1 - P_{FA}) P_{FA} + \dots + (1 - P_{FA})^{J - 1} P_{FA} \end{matrix}$ （18）

捕获J轮, 每轮都用门限判决方法, 其系统虚警率即为上述第一部分。

当卫星信号不存在时, 假设搜索U个单元格, 对所有单元格判决量进行排序, 则容易证明某个单元的判决量落在前K个的可能性为K/U。因此, 第二部分虚警率为:

$\begin{matrix} P_{fa 2} = \overset{J}{\sum_{z = 2}} C_{J}^{z} {(1 - K / U)}^{J - z} {(K / U)}^{z} (19) \end{matrix}$

由于第一与第二部分为互斥事件, 因此系统虚警率为P_fas=P_fa1+P_fa2。

3 仿真测试结果

使用自产生数据, 信号载噪比为26~31 dBHz, 多普频偏分别为:1000、-2345、3250、1700、4100、-4500 Hz, 伪码相位分别为:16、254、510、766、1020、1226, 进行10 000次捕获实验。数字中频量化为2 bit, 采样率为16 367 986 Hz, 中频为4 093 344 Hz, 降采样率为4.2 MHz, 相干积分总时间设为4 ms, 短时相关分段数为44, 搜索频点数为5, FFT运算点数为64, 但是只取32根谱线, 频率分辨率为172 Hz, 非相干累加次数为29。使用PC程序进行定点运算。

3.1 捕获统计量分析

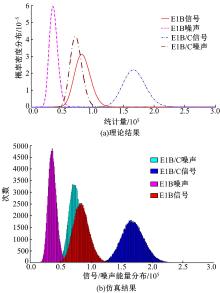
由图3可以看出, 捕获的能量分布仿真结果与理论结果比较吻合。

	Figure Option View Download New Window
	图3 31 dBHz 29次非相干累加的概率密度分布Fig.3 Probability density distribution at 31 dBHz and 29 non-coherent accumulations

3.2 捕获灵敏度分析

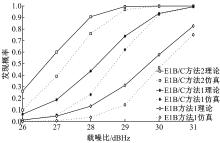
系统虚警率为0.002, E1B/C以及E1B捕获判决门限分别为125 700和73 670, 多普勒偏移门限f_th为200 Hz, 码片偏移门限th为2。J和K分别为2和10时的发现概率如图4所示。

	Figure Option View Download New Window
	图4 仿真发现概率和理论发现概率Fig.4 Simulated and theoretic detection probability

图4中方法1表示门限判决方法, 方法2表示门限加码相位判决方法。

从图4可以看出, 3种方法中E1B/C门限结合码相位判决方法发现概率最高, E1B门限判决方法发现概率最低。同时, 对于相同的载噪比信号, 仿真的发现概率低于理论的发现概率, 其主要原因是由于本地伪码和输入信号伪码相位差造成的。由于采样率约为2倍伪码速率, 因此理论上最大的伪码相位偏差可以达到1/4码片, 其引起的信号能量损失最大可以达到2 dB; 另外, FFT带来的频率模糊度也会降低系统发现概率。

从图4还可以看出, E1B/C联合捕获时, 使用基于恒虚警率的门限判决方法在载噪比为27 dBHz时仿真发现概率不到10%, 而使用门限结合码相位判决方法在载噪比为27 dBHz时仿真发现概率接近40%, 明显提高了捕获灵敏度。

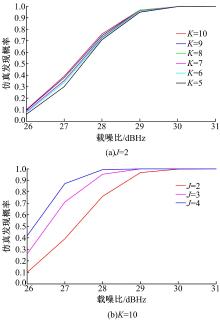
由图5(a)可以看出, 当J固定时, 随着K的增加, 系统发现概率呈递增趋势, 但这需要更多的存储空间以及比较时间。由图5(b)可以看出, 当K固定时, 随着J的增加, 系统发现概率也呈递增趋势, 但是这会带来捕获时间的增加。

	Figure Option View Download New Window
	图5 方法2系统发现概率(仿真结果)Fig.5 Detection probability of system 2(simulated results)

3.3 弱星最大捕获时间分析

本文提出了一种基于中频回放的联合捕获架构, 可根据中频回放时钟频率调整捕获速度。忽略FFT运算以及判决比较时间, 捕获一颗弱星最大时间计算公式如下:

$\begin{matrix} T_{\max} = 2 \times 2 \times J \times T_{Coh} \times P \times (S / Z) \times f_{num} \times (f_{down} / f_{play}) \end{matrix}$ (20)

式中:右边第一个2代表分时处理上、下边带; 第二个2代表分时处理E1B、E1C信号; S为需搜索半码片数, 值为8184; Z为相关支路数; f_num为搜索频点数; f_down为降采样后中频数据速率, 值为2.2 MHz; f_play为中频回放时钟频率。

卫星相干积分总时间为4 ms, 捕获轮数J为2, 非相干累加次数为29, 搜索频点数为5, 相关支路为1024时, 中频回放时钟频率分别为50、100、200 MHz三种情况下捕获一颗Galileo E1弱星最大时间分别为3.11、1.56和0.78 s。由此可以看出, 该捕获引擎回放时钟频率在200 MHz时捕获一颗弱星最长用时不足1 s, 完全能满足接收机实时性需求。

4 结束语

本文提出了一种基于中频回放的Galileo E1B/C联合捕获架构, 在不增加硬件规模下分时联合使用E1B/C信号相比只使用E1B或E1C信号在弱信号下明显地提高了发现概率; 并且捕获引擎工作在200 MHz时捕获一颗卫星最长用时不足1 s, 满足接收机实时性要求。同时, 本文提出了一种门限结合码相位判决方法, 与传统的门限判决方法相比, 该方法在弱信号情况下明显地提高了发现概率。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Mattos P G. Acquisition of the Galileo OAS L1B/C signal for the massmarket receiver[C]//ION GNSS 18th International Technical Meeting of the Satellite Division, Long Beach, CA, USA, 2005: 13-16. [本文引用:1]
[2]	Borio D, Presti L L. Data and pilot combining for composite GNSS signal acquisition[J]. International Journal on Navigation and Observation, DOI: DOI:10.1155/2008/738183. [本文引用:1]
[3]	Ta T H, Dovis F, Lesca R, et al. Comparison of joint data/pilot high-sensitivity acquisition strategies for indoor Galileo E1 signal[C]//European Navigation Conference ENC-GNSS, Toulouse, France, 2008: 23-25. [本文引用:1]
[4]	Adina Burian, Elena Simona Lohan, Markku Renfors. BPSK-like Methods for Hybrid-Search Acquisition of Galileo Signals[C]//IEEE International Conference on Communications, Istanbul, Turkey, 2006: 5211-5216. [本文引用:1]
[5]	Dovis F, Lesca R, Boiero G, et al. A test-bed implementation of an acquisition system for indoor positioning[J]. GPS Solution, 2010, 14(3): 241-253. [本文引用:1]
[6]	Musumeci L, Dovis F. Design of a very high sensitivity acquisition system for a space GNSS receiver[C]//IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, 2014: 556-568. [本文引用:1]
[7]	Choi I H, Park S H, Cho D J, et al. A novel weak signal acquisition scheme for assisted GPS[C]//15th Int Technical Meeting of the Satellite Division of the Institute of Navigation, Portland , OR, USA, 2002: 177-183. [本文引用:1]
[8]	Parks S H, Choi I H, Lee S J, et al. A novel GPS initial synchronization scheme using decomposed differential matched filter[C]//2002 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 2002: 246-253. [本文引用:1]
[9]	Schmid A, Neubauer A. Perfomance evaluation of differential correlation for single shot measurement positioning[C]//17th Int Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, 2004: 1998-2009. [本文引用:1]
[10]	Yu W, Zhen B, Watson R, et al. Differential combining for acquiring weak GPS signals[J]. Signal Process, 2007, 87(5): 824-840. [本文引用:1]
[11]	Kim Binhee, Kong Seung-Hyun. Two-dimensional compressed correlator for fast acquisition of CBOC-modulated signal in GNSS[C]//IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, 2014: 818-822. [本文引用:1]
[12]	Dovis F, Presti L L, Fantino M, et al. Comparison between Galileo CBOC cand idates and BOC(1, 1) in terms of detection performance[J]. Int J Navig Obs, 2008(2): 83-88. [本文引用:1]
[13]	巴晓辉. GPS基带接收机算法及其SoC芯片实现研究[D]. 北京: 中国科学院微电子研究所, 2007. Ba Xiao-hui. Research on algorithm and SoC implementation of GPS baseband receiver[D]. Beijing: Institute of Microelectronics of Chinese Academy of Sciences, 2007. [本文引用:1]
[14]	李健, 陈杰. 一种改进的北斗卫星信号并行捕获方法[J]. 宇航学报, 2014, 35(11): 1299-1305. Li Jian, Chen Jie. An improved parallel acquisition method for BDS signals[J]. Journal of Astronautics, 2014, 35(11): 1299-1305. [本文引用:1]
[15]	Borio D, Cmoriano L, Presti L L. Impact of GPS acquisiton strategy on decision probabilities[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(3): 996-1011. [本文引用:1]