用于遥感图像拼接的改进SURF算法

引用本文

董强, 刘晶红, 周前飞. 用于遥感图像拼接的改进SURF算法. 吉林大学学报（工学版）, 2017, 47(5): 1644-1652
DONG Qiang, LIU Jing-hong, ZHOU Qian-fei. Improved SURF algorithm used in image mosaic. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1644-1652 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705042
Permissions

用于遥感图像拼接的改进SURF算法

董强^1,², 刘晶红¹, 周前飞^1,²

1.中国科学院长春光学精密机械与物理研究所,长春 130033

2.中国科学院大学,北京 100049

通信作者:刘晶红(1967-),女,研究员,博士生导师.研究方向:机载光电成像测量.E-mail:liu1577@126.com

作者简介:董强(1989-),男,博士研究生.研究方向:遥感图像拼接技术.E-mail:dongqiang0518@126.com

基金项目:吉林省重大科技攻关项目(11ZDGG001); 装备预研项目; 国家林业公益性行业科研专项项目(201204515)

摘要

经典的SURF算法存在许多不足,如特征描述符维度高、运算量大,对于旋转和拍射视角变换角度过大时,匹配精度低等。针对以上问题,提出了一种改进算法,首先通过Hessian矩阵提取特征点,然后采用特征点圆形邻域进行特征描述,使用Haar小波响应为每个特征点建立描述符,同时计算邻域内归一化的灰度差分及二阶梯度,形成新的特征描述符,最后采用RANSAC算法剔除误匹配点。该算法不仅较经典SURF算法具有速度优势,同时充分利用了灰度信息和细节信息,具有更高的精度。实验结果表明:该算法对图像的模糊、光照差异、角度旋转、视场变换等均有良好的鲁棒性和稳定性。将该算法应用于遥感图像拼接,得到无明显几何移位、边缘衔接良好的拼接图像。该算法是一种耗时短、精度高的图像配准算法,能够满足遥感图像拼接对配准的要求。

关键词: 计算机应用; 图像配准; 特征提取; SURF算法; 二阶梯度

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2017)05-1644-09

Improved SURF algorithm used in image mosaic

DONG Qiang^1,², LIU Jing-hong¹, ZHOU Qian-fei^1,²

1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

2.University of Chinese Academy of Science, Beijing 100049, China

Abstract

To overcome the redundant feature descpriptor, high computational complexity, low matching precision when the angle of rotation or view spends greatly in image registration method based on SURF algorithm, an improved SURF algorithm is proposed. First, the feature points are extracted using Hessian matrix. Then, the feature descriptor for each keypoint in the circular neighborhood is constructed using Haar wavelet response; meanwhile, the normalized gray values difference and second-order gradient of this region are computed. Finally, RANSAC algorithm is applied to eliminate false matches. This method not only performs faster than SURF algorithm, but also fully employs the image gray information and details to acquire higher accuracy. Results indicate that the proposed method has strong robustness and stability for blur, illumination difference, angle rotation and viewpoint change. A well-edge mosaic image is obtained without obvious geometric misalignment in the remote sensing image mosaicking process. This method is an effective image registration algorithm with high-speed and precision, and it satisfies the need of registration in the remote sensing image mosaic.

Key words: computer application; image registration; feature extraction; SURF algorithm; second-order gradient

Show Figures

0 引言

近年来, 随着计算机技术的飞速发展, 图像处理技术也得到空前的提升, 作为其重要组成部分的图像配准已经广泛应用于图像拼接、目标识别、医学图像处理等各领域^[1]。图像配准技术的方法大体分为两类:基于灰度信息的配准方法和基于特征的配准方法^[2]。基于灰度的图像配准方法较为简单, 直接计算两图像灰度值的关系来匹配图像, 这种方法虽然简单、易实现, 但其稳定性差, 对光照变化敏感。相比之下, 基于特征的配准方法具有良好的稳定性, 在克服图像的光照、尺度、旋转等变化具有更好的鲁棒性, 是目前主流的图像配准方法^[3]。

为了提高配准精度和速度, 学者们对图像的特征进行了许多研究, 如图像的点特征^{[4, 5, 6]}、轮廓特征^{[7, 8]}、边缘特征^{[9, 10]}等。SIFT(Scale invariant feature transform)特征检测算法^{[11, 12, 13, 14]}是基于尺度空间的, 对于图像的各种变化都具有良好的适应性, 但是, SIFT也存在着算法复杂、耗时长、计算效率较低等问题。PCA-SIFT^[15]是SIFT的改进算法, 该算法大大提高了SIFT的匹配速度, 但是其鲁棒性不如SIFT。Bay等^[16]于2006年提出了一种SIFT的改进算法— — SURF(Speeded up robust feature)算法。该算法速度更快且性能稳定, 但仍存在特征描述符复杂, 运算量大, 对于旋转和视场角度变换过大时, 匹配精度低等问题。

针对上述问题, 本文提出一种改进的特征描述符, 将SURF算法的方形邻域变为同心圆环, 同时, 加入图像的灰度特征及二阶梯度特征, 使其具有更好的稳定性, 特征描述符由64维降到26维, 减少特征匹配耗时, 提高运行速度。最后, 使用RANSAC (Random sample consensus)^{[17, 18]}进行误匹配点剔除, 提高精度。

1 SURF算法

经典的SURF算法主要分为以下4个步骤完成。

(1)特征点提取。选取不同尺寸的盒子滤波器生成图像的尺度空间, 利用快速Hessian矩阵行列式确定特征点的位置, 同时在尺度空间和图像空间插值, 精确定位特征点的尺度和位置。

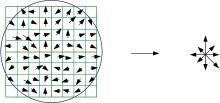
(2)主方向分配。以特征点为圆心, 6S(S为尺度)为半径的圆, 计算y方向和x方向的Haar小波响应, 并根据距离特征点远近进行高斯加权, 统计60° 扇形内的响应, 计算响应之和, 以小角度(一般为5° )旋转扇形遍历整个圆, 选取最大值方向为该点的主方向。

(3)描述符生成。以特征点为中心旋转坐标轴到主方向后, 选取边长为20S的正方形区域, 并将其划分为16个子区域(每个子区域大小为5S× 5S), 计算每一点的Haar小波响应, 并赋给权值, 统计每个子区域的水平、垂直方向的响应及其绝对值, 这样就可得到一个64维的特征描述符。

(4)特征点匹配。采用最小欧氏距离准则来进行特征点匹配。

虽然SURF算法在工程上具有广泛的应用, 但其特征描述符冗余、计算量大, 不能满足工程中实时性的要求, 当两幅图像光照变化强烈时, 其匹配效果不理想, 同时, 对于图像配准中经常出现的大角度旋转和三维视角变换等问题, SURF算法也不能满足要求。

2 改进算法

针对经典SURF算法中存在的问题, 本文从以下3个方面进行改进。

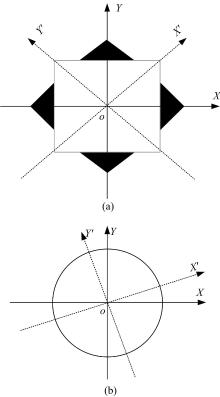
(1)采用圆形邻域进行特征描述符的提取。经典SURF算法的主方向确定对于特征点描述符的生成起着至关重要的作用。SURF算法的描述符准确与否依赖于主方向的确定。经典SURF算法采用矩形区域进行特征描述符的计算, 当主方向确定出现误差时, 其描述符计算区域会发生变化, 如图1(a)所示。本文采用圆型区域计算特征描述符, 当主方向存在误差时, 其计算区域相同, 如图1(b)所示。

	Figure Option View Download New Window
	图1 矩形与圆形区域比较Fig.1 Comparison of square with circular area

(2)引入区域灰度值差分作为特征描述符的一部分, 可在一定程度上克服光照对于配准的影响。

(3)引入二阶梯度值作为特征描述符的扩展。二阶梯度值是图像纹理细节信息的一种直观反映^[19], 为了更好地利用图像的细节, 本文将二阶梯度引入特征描述符, 以增加算法的鲁棒性和健壮性。本文使用的二阶梯度计算方法如下:

记图像I(x, y)的灰度值为f(x, y), 在数字图像中以差分来近似替代导数, 以g_y(x, y)表示该点在y方向上的一阶梯度, 其计算式为:

$\begin{matrix} \begin{matrix} g_{y} (x, y) = \\ f (x, y + 1) + f (x, y + 2) + f (x, y + 3) - \\ [f (x, y - 1) + f (x, y - 2) + f (x, y - 3)] \end{matrix} \end{matrix}$ （1）

图像在该点的y方向二阶梯度值记为h_y(x, y), 其计算式为:

$\begin{matrix} \begin{matrix} h_{y} (x, y) = \\ g_{y} (x, y + 1) + g_{y} (x, y + 2) + g_{y} (x, y + 3) - \\ [g_{y} (x, y - 1) + g_{y} (x, y - 2) + g_{y} (x, y - 3)] \end{matrix} \end{matrix}$ （2）

将式(1)代入式(2), 整理可得:

$\begin{matrix} h_{y} (x, y) = \overset{6}{\sum_{i = - 6}} f (x, y + i) t [i] \end{matrix}$ (3)

式中:t[i]为系数矩阵, t[i]=[0, 1, 2, 1, 0, -2, -4, -2, 0, 1, 2, 1, 0]。

同理, 可以求出x方向的二阶梯度为:

$\begin{matrix} h_{x} (x, y) = \overset{6}{\sum_{i = - 6}} f (x + i, y) t [i] \end{matrix}$ (4)

图像点I(x, y)的二阶梯度和方向计算式为:

$h (x, y) = \sqrt[]{h_{x} {(x, y)}^{2} + h_{y} {(x, y)}^{2}}$ (5)

$\begin{matrix} θ (x, y) = ta n^{- 1} (h_{y} (x, y) / h_{x} (x, y)) \end{matrix}$ （6）

2.1 特征点提取与主方向确定

本文算法与SURF前两步其本一致。首先, 用不同尺寸的滤波器模板构建尺度空间提取特征点, 本文算法在提取特征点时进行边缘抑制, 去除过边缘点, 为后面的步骤节省时间。然后, 确定主方向, 以特征点为中心, 将坐标轴旋转到主方向。

2.2 特征描述符生成

(1)以特征点为中心, 选取半径分别为r₁=3 $\begin{matrix} \sqrt[]{2} \end{matrix}$ S、r₂=5 $\begin{matrix} \sqrt[]{2} \end{matrix}$ S、r₃=7 $\begin{matrix} \sqrt[]{2} \end{matrix}$ S(S为特征点的尺度)的同心圆。3个同心圆将特征描述区域分割成3个子区域, 即:一个中心圆和两个圆环, 如图2所示。

	Figure Option View Download New Window
	图2 特征点邻域分割方式Fig.2 Split of square region centered around interest point

(2)在每一个子区域计算每一个点在水平方向和垂直方向上的Haar小波响应值, 同时将以特征点为中心的高斯加权系数赋予这些响应值, 以达到增强算法稳健性的目的, 然后计算每个子区域响应值的和。这样, 每一个子区域就得到V_sub:

$\begin{matrix} V_{sub} = (\sum dx, \sum | dx |, \sum dy, \sum | dy |) \end{matrix}$ （7）

由式(7)可知, 该步特征描述符是3× 4=12维的。表示为:D=(d₁, d₂, …, d₁₂), 将D进行归一化:

$\begin{matrix} \bar{D} = \frac{D}{\sqrt[]{\overset{12}{\sum_{i = 1}} d_{i}^{2}}} = ({\bar{d}}_{1}, {\bar{d}}_{2}, \dots, {\bar{d}}_{12}) \end{matrix}$ （8）

(3)计算区域的灰度值之和, 记:半径为r₁、r₂、r₃的圆内区域像素的灰度值之和分别为f₁、f₂、f₃, 得到一个三维描述符:F=(f₁, f₂, f₃)。将F=(f₁, f₂, f₃)进行归一化处理:

$\begin{matrix} \bar{F} = \frac{F}{\sqrt[]{\overset{3}{\sum_{j = 1}} f_{j}^{2}}} = ({\bar{f}}_{1}, {\bar{f}}_{2}, {\bar{f}}_{3}) \end{matrix}$ （9）

(4)根据步骤(3)得到的( $\begin{matrix} {\bar{f}}_{1} \end{matrix}$ , $\begin{matrix} {\bar{f}}_{2} \end{matrix}$ , $\begin{matrix} {\bar{f}}_{3} \end{matrix}$ )计算3个圆形区域的差分值:

$\begin{matrix} \{\begin{matrix} d {\bar{f}}_{1} = | {\bar{f}}_{1} - {\bar{f}}_{2} | \\ d {\bar{f}}_{2} = | 2 {\bar{f}}_{2} - {\bar{f}}_{1} - {\bar{f}}_{3} | \\ d {\bar{f}}_{3} = | {\bar{f}}_{3} - {\bar{f}}_{2} | \end{matrix} \end{matrix}$ （10）

(5)根据式(5)(6)计算半径为r₃的圆内所有点的二阶梯度值及方向, 并赋予以特征点为中心的高斯加权系数, 然后, 计算8个方向的二阶梯度和, 生成一个8维向量(h₁, h₂, h₃, h₄, h₅, h₆, h₇, h₈), 并进行归一化, 生成8维向量( $\begin{matrix} {\bar{h}}_{1} \end{matrix}$ , $\begin{matrix} {\bar{h}}_{2} \end{matrix}$ , $\begin{matrix} {\bar{h}}_{3} \end{matrix}$ , $\begin{matrix} {\bar{h}}_{4} \end{matrix}$ , $\begin{matrix} {\bar{h}}_{5} \end{matrix}$ , $\begin{matrix} {\bar{h}}_{6} \end{matrix}$ , $\begin{matrix} {\bar{h}}_{7} \end{matrix}$ , $\begin{matrix} {\bar{h}}_{8} \end{matrix}$ ), 如图3所示。

	Figure Option View Download New Window
	图3 特征点邻域二阶梯度描述符Fig.3 Descriptor of second-order gradient of feature point’ s neighborhood

(6)生成26维描述符:

$\begin{matrix} D = ({\bar{d}}_{1}, {\bar{d}}_{2}, \dots, {\bar{d}}_{12}, {\bar{f}}_{1}, {\bar{f}}_{2}, {\bar{f}}_{3}, d {\bar{f}}_{1}, d {\bar{f}}_{2}, d {\bar{f}}_{3}, {\bar{h}}_{1}, {\bar{h}}_{2}, \dots, {\bar{h}}_{8}) \end{matrix}$ （11）

2.3 特征点匹配

采用最小欧氏距离准则进行特征点匹配。计算特征向量的最小欧氏距离和次小欧氏距离的比值, 记:待配准图像中与参考图像特征点欧氏距离最近的两个关键点的欧氏距离为d₁、d₂。

$\begin{matrix} \frac{d_{1}}{d_{2}} < T \end{matrix}$ (12)

设定阈值T(一般为0.6~0.8, 本文取0.6), 若比值小于阈值则认为两点为正确匹配点对, 遍历所有特征点, 得到全部匹配点对。

2.4 误匹配点剔除

由上述度量方法进行匹配的特征点会存在一定的误匹配点, 故本文采用RANSAC算法剔除误匹配点, 提高匹配正确率。RANSAC是随机采样一致性算法, 此算法的原理为:随机选取m个点计算模型参数, 然后利用得到的模型衡量其他点, 把小于阈值的点作为内点。重复以上过程n次, 选择内点最多的点集计算准确的模型参数。该算法不仅可以有效剔除大量误匹配点, 还可以得到鲁棒性更好的估计结果。

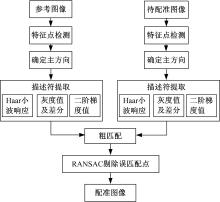
综上所述, 图像配准算法流程如图4所示。

	Figure Option View Download New Window
	图4 算法流程Fig.4 Flow chart of algorithm

3 实验结果与分析

针对本文提出的改进SURF算法, 采用了大量图像进行了图像配准实验, 并将本文算法与SIFT算法和SURF算法进行比较, 对其匹配性能进行了定量评价与分析。同时, 将本文算法用于遥感图像拼接, 并对拼接精度进行评价。

3.1 运行环境

算法运行环境如下:CPU为Intel core i5, 3.20 GHz, 内存为4 GB的PC机, 32位Win7操作系统, 仿真软件为Matlab 8.1.0.604(R2013a)。

3.2 评价指标

本文采用3个参数对图像匹配的效果进行综合评价。

(1)采用运行时间(加上RANSAC算法时间)对匹配速度进行评价。

(2)采用匹配性能客观评价指标— — 匹配正确率CMR(Correct matching rate), CMR值越大, 匹配性能越好, CMR定义如下:

$\begin{matrix} CMR = \frac{N_{c}}{N} \end{matrix}$ （13）

式中:N为所有匹配点对数; N_c为正确匹配点对数。

(3)采用均方根误差RMSE(Root mean square error)进行参考图像与配准后图像之间的距离度量, 两者距离越大, 则RMSE的值越大, 说明配准精度越低, 配准效果越差, 反之, 配准效果越好^[20]。RMSE的计算公式如下:

$\begin{matrix} RMSE = \sqrt[]{\frac{1}{M} \overset{M}{\sum_{i = 1}} ‖(x_{i}, y_{i}) - f (x'_{i}, y'_{i}) ‖^{2}} (14) \end{matrix}$

式中:M为最终匹配点对的数目; (x'_i, y'_i)为待配准图像中特征点的坐标; (x_i, y_i)为参考图像中特征点的坐标; f(· )为仿射变换模型。

3.3 配准实验结果

采用4对测试图像分别对算法的抗模糊、光照、旋转、视角变换性能进行测试, 如图5(a)~(d)所示, 图像尺寸分别为1000× 700、800× 640、850× 680、800× 640像素, 使用SIFT算法、SURF算法和本文算法进行配准。

	Figure Option View Download New Window
	图5 四组测试图像Fig.5 Four groups of test image

表1为匹配运算时间, 表2为匹配点对和正确率, 表3为配准精度评价指标(均方根误差)。

表1 运算时间 Table 1 Run time s

表2 匹配点对和正确率 Table 2 Matching pairs and correct matching rate

表3 均方根误差 Table 3 Root mean square error

由表1可以看出, 本文算法用时比SIFT算法和SURF算法更少, 相较于SIFT算法和SURF算法, 速度分别提高97.61%和22.94%。尤其当图像复杂度较高时, 本文算法速度优势明显, 这是因为本文采用26维描述符, 大大减少了特征描述符提取和匹配用时, 故此算法具有速度优势。

由表2可以看出, SIFT算法在抗模糊、光照、旋转方面性能优越, 提取出的提征点多且匹配正确率高, 但其对视角变换提取的特征点较少, 往往不能满足要求。本文算法匹配正确率均高于SURF算法, 且对于光照、旋转、视角变化均有显著提高, 相较于SURF算法, 匹配正确率平均提高10.84%。

由表3可以看出, SIFT算法RMSE值最小, 匹配精度最高。本文算法RMSE的值均小于SURF算法, 平均减小22.61%, 算法精度提高。

3.4 遥感图像拼接精度评价

在获得两幅图像的精确匹配特征点对后, 由式(15)图像变换关系可以求解出变换矩阵H, 将待配准图像I'通过H进行变换后与参考图像I进行叠加, 就可得到拼接图像。

$\begin{matrix} [\begin{matrix} x' \\ y' \\ 1 \end{matrix}] = H [\begin{matrix} x \\ y \\ 1 \end{matrix}] = [\begin{matrix} h_{0} & h_{1} & h_{2} \\ h_{3} & h_{4} & h_{5} \\ h_{6} & h_{7} & h_{8} \end{matrix}] [\begin{matrix} x \\ y \\ 1 \end{matrix}] \end{matrix}$ (15)

式中:(x', y')和(x, y)分别为待配准图像I'和参考图像I的匹配点对。

采用图6所示的两幅图像进行拼接精度测试, 人为在图像的重叠区域加入十字监测点, 图6(a)中绿色的点和图6(b)中红色的点是人为加入的3组十字监测点, 每组含17个独立点。

	Figure Option View Download New Window
	图6 加入十字监测点Fig.6 Join cross monitoring points

对图像进行拼接, 并高亮显示重叠区域, 得到图7所示图像。将其中一组监测点放大并标记每个点的序号, 如图8所示。记录每个监测点的坐标, 并求出每个监测点间的距离, 对其他两组十字监测点进行相同操作。

	Figure Option View Download New Window
	图7 带监测点的拼接图像Fig.7 Mosaic images with monitoring points

	Figure Option View Download New Window
	图8 监测点区域放大图像Fig.8 Magnified image with monitoring points

	Figure Option View Download New Window
	图9 监测点距离比较图Fig.9 Monitoring points distance comparison table

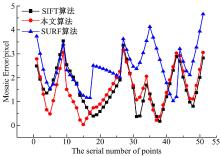
对图6中的两幅图像分别采用SIFT算法、SURF算法和本文算法进行拼接实验, 记录各监测点间的距离的均方根误差(RMSE)。将3种算法的实验数据进行对比, 如图9所示。由图9可以看出, 本文算法的平均RMSE=1.2653, SURF算法的平均RMSE=1.8727, SIFT算法的平均RMSE=1.2275。由以上数据对比可知, 使用本文算法获得的拼接图像精度虽较SIFT算法略低, 但较SURF算法有显著提高, 平均提高32.43%。

	Figure Option View Download New Window
	图10 图像拼接比较Fig.10 Comparison of image masoic

3.5 遥感图像拼接结果

分别使用SURF算法和本文算法对图像进行拼接实验, 放大拼接边缘, 如图10所示。由图10(b)(c)可以看出, 使用SURF算法拼接图像精度较差, 有明显几何错位, 由图10(e)(f)可以看出, 本文算法无明显的几何错位, 边缘衔接良好, 拼接精度较SURF算法有显著提高。

最后, 针对两图像亮度差异产生的明显接缝, 采用加权平滑算法对图像进行平滑处理, 得到亮度变化均匀、无明显接缝、无鬼影、保真度高的拼接图像, 如图11所示。

	Figure Option View Download New Window
	图11 拼接图像Fig.11 Image mosaic result

4 结束语

针对经典SURF算法存在的运行时间长、对于大角度旋转及视角变化配准效果差的问题, 本文提出一种全新的特征描述符, 将经典SURF算法特征描述符提取采用的方形区域改变为同心圆环区域, 大大加强了算法的稳健性。同时, 利用归一化的灰度差分描述该区域的灰度特征, 从而令其对光照变化有更好的稳健性。引入区域内的二阶梯度因子, 更充分地利用图像的细节信息, 增强了算法的鲁棒性和适应性。最后, 采用RANSAC算法剔除误匹配点, 进一步提高算法的配准精度。将特征描述符从64维降至26维, 大大减少了特征提取及匹配用时, 使该算法具有速度优势。实验证明本文算法对图像的模糊、光照、旋转缩放及视角变化都优于经典SURF算法, 同时算法运行耗时更少。本文算法能够有效利用图像的细节信息, 提高匹配正确率, 为图像拼接提供更为准确的变换模型。在遥感图像拼接实验中, 本文算法精度高, 较SURF算法有明显提高, 拼接边缘无明显错位, 衔接良好。本文算法速度快、耗时短, 在遥感图像拼接等实时性要求高等领域具有现实意义, 为向高速实时图像处理硬件平台的移植提供可能。综上所述, 本文算法相较SURF算法更具优越性, 是一种有快速、稳定、有效的图像配准新方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	席海峰, 田超. 基于 SVR 的宽基线图像匹配方法[J]. 重庆邮电大学学报: 自然科学版, 2013, 25(2): 197-202. Xi Hai-feng, Tian Chao. Wide baseline image matching using support vector regression[J]. Journal of Chongqing University of Posts & Telecommunications(Natural Science Edition), 2013, 25(2): 197-202. [本文引用:1]
[2]	杨光, 田地, 李军, 等. 基于投影特征的快速图像匹配方法[J]. 吉林大学学报: 工学版, 2010, 40(5): 1340-1344. Yang Guang, Tian Di, Li Jun, et al. Fast image matching method based on projective feature[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(5): 1340-1344. [本文引用:1]
[3]	余先川, 吕中华, 胡丹. 遥感图像配准技术综述[J]. 光学精密工程, 2013, 21(11): 2960-2972. Yu Xian-chuan, Lyu Zhong-hua, Hu Dan. Review of remote sensing image registration technique[J]. Optics and Precision Engineering, 2013, 21(11): 2960-2972. [本文引用:1]
[4]	颜雪军, 赵春霞, 袁夏. 一种鲁棒的基于图像对比度的局部特征描述方法[J]. 电子与信息学报, 2014, 36(4): 882-887. Yan Xue-jun, Zhao Chun-xia, Yuan Xia. A robust local feature descriptor based on image contrast[J]. Journal of Electronics & Information Technology, 2014, 36(4): 882-887. [本文引用:1]
[5]	安建妮, 刘贵喜. 利用特征点配准和变换参数自动辨识的图像拼接算法[J]. 红外与激光工程, 2011, 40(3): 564-569. An Jian-ni, Liu Gui-xi. Image mosaic algorithm base on feature points matching and automatic transform parameters identifying[J]. Infrared and Laser Engineering, 2011, 40(3): 564-569. [本文引用:1]
[6]	Wang Wei-xing, Cao Ting, Liu Sheng, et al. Remote sensing image automatic registration on multi-scale harris-laplacian[J]. Indian Soc Remote Sens, 2015, 43(3): 501-511. [本文引用:1]
[7]	Olszewska J I. Active contour based optical character recognition for automated scene understand ing[J]. Neurocomputing, 2015, 161: 65-71. [本文引用:1]
[8]	Zhang Jian-wei, Huang Da-cheng, Gui Jiang-qin, et al. 2D registration based on contour matching for partial matching images[J]. Journal of Central South University, 2014, 21(12): 4553-4562. [本文引用:1]
[9]	Sutour C, Aujol J F, Deledalle C A, et al. Edge-based multi-modal registration and application for night vision devices[J]. Journal of Mathematical Imaging and Vision, 2015, 53(2): 131-150. [本文引用:1]
[10]	Zhang Han, Ni Wei-ping, Yan Wei-dong. Robust SAR image registration based on edge matching and refined coherent point drift[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12: 2115-2119. [本文引用:1]
[11]	Lowe D G. Object recognition from local scaleinvariant features[C]//Proceedings of the 7th International Conference on Computer Vision, Corfu, Greece, 1999: 1150-1157. [本文引用:1]
[12]	Lowe D G. Distinctive Image features from scale-invariant key points[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. [本文引用:1]
[13]	汪松, 王俊平, 万国挺, 等. 基于SIFT算法的图像匹配方法[J]. 吉林大学学报: 工学版, 2013(增刊1): 279-282. Wang Song, Wang Jun-ping, Wan Guo-ting, et al. Image matching method based on SIFT algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2013(Sup. 1): 279-282. [本文引用:1]
[14]	曾峦, 王元钦, 谭久彬. 改进的SIFT特征提取和匹配算法[J]. 光学精密工程, 2011, 19(6): 1391-1397. Zeng Luan, Wang Yuan-qin, Tan Jiu-bin. Improved algorithm for SIFT feature extraction and matching[J]. Optics and Precision Engineering, 2011, 19(6): 1391-1397. [本文引用:1]
[15]	Ke Y, Sukthankar R. PCA-SIFT: a more distinctive representation for local image descriptors[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington DC, USA, 2004: 506-513. [本文引用:1]
[16]	Bay H, Tuytelaars T, Gool L. SURF: speeded up robust features[C]//Proceedings of the 9th European Conference Computer Vision, IEEE, 2006: 404-417. [本文引用:1]
[17]	谷宗运, 谭红春, 殷云霞, 等. 基于SURF和改进的RANSAC算法的医学图像配准[J]. 中国医学影像学杂, 2014, 22(6): 470-475, 480. Gu Zong-yun, Tan Hong-chun, Yin Yun-xia, et al. Medical image registration based on SURF and improved RANSAC algorithm[J]. Chinese Journal of Medical Imaging, 2014, 22(6): 470-475, 480. [本文引用:1]
[18]	Misra I, Moorthi S M, Dhar D, et al. An automatic satellite image registration technique based on harris corner detection and rand om sample consensus (RANSAC) outlier rejection model[C]//International Conference on Recent Advances in Information Technology, IEEE, 2012: 68-73. [本文引用:1]
[19]	Chen Q, Montesinos P, Sun Q S, et al. Adaptive total variation denoising based on difference curvature[J]. Image and Vision Computing, 2010, 28: 298-306. [本文引用:1]
[20]	Zhang R J, Zhang J Q, Yang C. Image registration approach based on SURF[J]. Infrared and Laser Engineering, 2009, 38(1): 160-165. [本文引用:1]

2013

0.0

. 2013, 25(2):197-202 DOI:doi:10.3979/j.issn.1673-825X.2013.02.011

Wide baseline image matching using support vector regression

SVR 的宽基线图像匹配方法

Xi Hai-feng , Tian Chao.

席海峰, 田超, .基于

针对宽基线图像匹配处理中的误匹配问题,使用支持向量回归(support vector regression,SVR)方法来解决宽基线图像匹配,采用了一种改进的拓扑过滤器新算法来剔除误匹配。改进拓扑过滤机制匹配大量SIFT(scale-in-variant feature transform)特征,剔除一些误匹配项获得高正确率的初始匹配,实现使用高正确率的初始匹配来构建SVR;同时,基于构建SVR关系给出的预测值附件搜索新的匹配。在宽基线条件下对室内和室外的环境图像进行测试实验,结果表明,该算法能够自动获取大量正确匹配。

... 0 引言近年来,随着计算机技术的飞速发展,图像处理技术也得到空前的提升,作为其重要组成部分的图像配准已经广泛应用于图像拼接、目标识别、医学图像处理等各领域^[1] ...

2010

0.0

. 2010, 40(5):1340-1344

Fast image matching method based on projective feature

基于投影特征的快速图像匹配方法

Yang Guang , Tian Di , Li Jun

杨光, 田地, 李军

... 图像配准技术的方法大体分为两类:基于灰度信息的配准方法和基于特征的配准方法^[2] ...

2013

0.0

. 2013, 21(11):2960-2972 DOI:doi:10.3788/OPE.20132111.2960

Review of remote sensing image registration technique

遥感图像配准技术综述

Yu Xian-chuan , Lyu Zhong-hua , Hu Dan.

余先川, 吕中华, 胡丹

Remote sensing image registration is an indispensable part for remote sensing image fusion, multispectral classification, environmental monitoring, image mosaicing and so on. In this paper, the important and latest registration methods for remote sensing are discussed and are divided into four types, including area-based methods, feature-based methods, hybrid-based model methods and physically-based model methods. Then, the classic algorithms of each type are analyzed respectively, and their advantages and shortcomings are also stated. The scale invariant feature transform algorithms are mainly discussed. Furthermore, the difficulties of remote sensing image registration techniques are summarized, including the multi-source remote sensing image registration, the real-time registration of remote sensing image, the nonlinear registration of remote sensing image and the accuracy evaluation of remote sensing image registration. Finally, the prospects of image registration are pointed out.

遥感图像配准是图像融合、多光谱分类、环境监测和图像镶嵌等不可缺少的步骤。本文讨论了遥感图像领域中重要的和最新的配准算法，将配准方法划分为基于区域的配准、基于图像特征的配准、基于混合模型的配准和基于物理模型的配准四类；描述了四类配准方法中的典型算法，并分析了它们的优势和不足，重点概述了基于特征配准中的局部不变特征变换算法。评述了国内外遥感图像配准的发展现状；指出了遥感图像配准技术中存在的问题，即多源遥感图像的配准、遥感图像配准的实时性、遥感图像的非线性配准和遥感图像配准的精度评价，最后展望了遥感图像配准技术的发展前景。

... 相比之下,基于特征的配准方法具有良好的稳定性,在克服图像的光照、尺度、旋转等变化具有更好的鲁棒性,是目前主流的图像配准方法^[3] ...

2014

0.0

. 2014, 36(4):882-887

A robust local feature descriptor based on image contrast

一种鲁棒的基于图像对比度的局部特征描述方法

Yan Xue-jun , Zhao Chun-xia , Yuan Xia.

颜雪军, 赵春霞, 袁夏

... 为了提高配准精度和速度,学者们对图像的特征进行了许多研究,如图像的点特征^[4,5,6]、轮廓特征^[7,8]、边缘特征^[9,10]等 ...

2011

0.0

. 2011, 40(3):564-569 DOI:doi:10.3969/j.issn.1007-2276.2011.03.038

Image mosaic algorithm base on feature points matching and automatic transform parameters identifying

利用特征点配准和变换参数自动辨识的图像拼接算法

An Jian-ni , Liu Gui-xi.

安建妮, 刘贵喜

提出了一种不同尺度的图像配准与自适应拼接算法。通过特征点匹配与图像间变换几何参数的自动辨识,实现了不同尺度和旋转图像间的匹配和拼合。利用尺度不变特征点提取算法(SIFT)提取出待拼接图像的特征点,根据互信息量最大原则实现特征点的匹配,然后通过得到的匹配对的几何信息自动辨识出两幅图像之间的变换参数关系,得到反映图像平移、旋转和尺度变换信息的投影变换矩阵,最终实现图像的无缝融合拼接。仿真结果表明:与现有算法相比,该算法较好地解决了不同尺度图像间的配准与自适应拼合问题。

... 为了提高配准精度和速度,学者们对图像的特征进行了许多研究,如图像的点特征^[4,5,6]、轮廓特征^[7,8]、边缘特征^[9,10]等 ...

2015

0.0

... 为了提高配准精度和速度,学者们对图像的特征进行了许多研究,如图像的点特征^[4,5,6]、轮廓特征^[7,8]、边缘特征^[9,10]等 ...

2015

0.0

... 为了提高配准精度和速度,学者们对图像的特征进行了许多研究,如图像的点特征^[4,5,6]、轮廓特征^[7,8]、边缘特征^[9,10]等 ...

2014

0.0

... 为了提高配准精度和速度,学者们对图像的特征进行了许多研究,如图像的点特征^[4,5,6]、轮廓特征^[7,8]、边缘特征^[9,10]等 ...

2015

0.0

... 为了提高配准精度和速度,学者们对图像的特征进行了许多研究,如图像的点特征^[4,5,6]、轮廓特征^[7,8]、边缘特征^[9,10]等 ...

2015

0.0

... 为了提高配准精度和速度,学者们对图像的特征进行了许多研究,如图像的点特征^[4,5,6]、轮廓特征^[7,8]、边缘特征^[9,10]等 ...

1999

0.0

... SIFT(Scale invariant feature transform)特征检测算法^{[11,12,13,14]}是基于尺度空间的,对于图像的各种变化都具有良好的适应性,但是,SIFT也存在着算法复杂、耗时长、计算效率较低等问题 ...

2004

0.0

. , 2013(增刊1):279-282

Image matching method based on SIFT algorithm

基于SIFT算法的图像匹配方法

Wang Song , Wang Jun-ping , Wan Guo-ting

汪松, 王俊平, 万国挺

摘　要：依据Brown的理论,并基于SIFT算法提出了一种有效的图像匹配方法。首先对图像进行高斯和Wallis滤波处理,然后采用简化SIFT算法进行特征点提取,最后通过特征点双向匹配方法实现图像的精确匹配。通过对缺陷版图图像的试验验证了该方法具有匹配点数量多、准确率高、无重复点等优点。将该方法应用于优化线网的自动检测方面得到较好的效果,并为版图的优化打下了基础。

2011

0.0

. 2011, 19(6):1391-1397 DOI:doi:10.3788/OPE.20111906.1391

Improved algorithm for SIFT feature extraction and matching

改进的SIFT特征提取和匹配算法

Zeng Luan , Wang Yuan-qin , Tan Jiu-bin.

曾峦, 王元钦, 谭久彬

A robust automated image matching strategy based on an improved SIFT feature extraction algorithm was proposed according to the characteristics of SIFT algorithm and lunar images. Firstly, the extraction equilibrium of key points was improved by automatically adjusting the coefficient of controlling contrast in the SIFT algorithm.Then, the coarse matching was carried out by using the ratio of the minimum and the second minimum Euclidean distance between the description vectors of SIFT as a threshold and the part incorrect matching of the coarse matching set was removed by principal direction angle difference histogram of matches. Finally, the initial parameters of perspective transformation model were determined by using modified RANSAC method, automatically calculated random sampling numbers, and parameters of error tolerance. Moreover, the model and the error tolerance were used to calibrate the matching pairs in the matching set and to select the correct matching pairs. The experimental results prove that the proposed method is stable and reliable under some variations for view points, illumination, rotation, scale and out of focus and it can select the matching threshold of images automatically without manual intervention.

针对月球影像和尺度不变特征变换(SIFT)算法的特点,在改进SIFT特征提取算法的基础上,提出了一种稳健的图像自动匹配策略。首先,自动调整SIFT算法中的对比度控制系数,提高关键点提取的均衡性;然后,用SIFT描述向量之间的欧氏距离最小值与次小值的比值作为阈值,进行粗匹配,并利用匹配对主方向角度差直方图剔除部分伪匹配;最后,自动计算随机采样次数、误差容忍度等参数,使用改进的随机选取一致性(RANSAC)方法确定透视变换模型初始参数,并用该模型和误差容忍度对匹配集合中的匹配对进行校验,选取出正确的匹配对。实验结果表明,在图像有一定程度的视点、光照、旋转、比例、模糊和对比度变化等情形下,该算法稳定、可靠。该方法能有效解决图像匹配门限的选择问题,真正实现了无人工干预的自动匹配。

2004

0.0

... PCA-SIFT^[15]是SIFT的改进算法,该算法大大提高了SIFT的匹配速度,但是其鲁棒性不如SIFT ...

2006

0.0

... Bay等^[16]于2006年提出了一种SIFT的改进算法#cod#x02014 ...

2014

0.0

. 2014, 22(6):470-475, 480

Medical image registration based on SURF and improved RANSAC algorithm

基于SURF和改进的RANSAC算法的医学图像配准

Gu Zong-yun , Tan Hong-chun , Yin Yun-xia

谷宗运, 谭红春, 殷云霞

... 最后,使用RANSAC (Random sample consensus)^[17,18]进行误匹配点剔除,提高精度 ...

2012

0.0

... 最后,使用RANSAC (Random sample consensus)^[17,18]进行误匹配点剔除,提高精度 ...

2010

0.0

... 二阶梯度值是图像纹理细节信息的一种直观反映^[19],为了更好地利用图像的细节,本文将二阶梯度引入特征描述符,以增加算法的鲁棒性和健壮性 ...

2009

0.0

... (3)采用均方根误差RMSE(Root mean square error)进行参考图像与配准后图像之间的距离度量,两者距离越大,则RMSE的值越大,说明配准精度越低,配准效果越差,反之,配准效果越好^[20] ...