偏X型细胞自动机与经典T型细胞自动机原理一致, 这种可逆的细胞自动机依靠相邻2个时刻的全局状态演化, 而初始迭代是没有前驱状态的, 因此我们通过另一个混沌规则细胞自动机, 以明文图像信息为种子, 演化出一个初始状态S₁的前驱S₀。偏X型邻居细胞自动机具有T型邻居细胞自动机的特征, 如果细胞的当前时刻邻居状态相同, 而前一时刻状态不同, 其邻域函数规则演化状态互补, 则该细胞自动机是可逆并且其逆细胞自动机就是其自身。

S^t+1=F(S^t, S^t-1)关系式表达了下一时刻状态由前面相邻两状态决定。

以X型邻居为例说明, 对于 Si, jt+1=f( Si-1, j-1t, Si-1, j+1t, Si, jt, Si+1, j-1t, Si+1, j+1t, Si, jt-1), 若有 Si, jt+1= Si, jt-1, 则有 Si, jt-1=f( Si-1, j-1t, Si-1, j+1t, Si, jt, Si+1, j-1t, Si+1, j+1t, Si, jt+1), 若二者不等, 则有 Si, jt+1= S-i, jt-1(互补状态), 可推出: S-i, jt-1=f( Si-1, j-1t, Si-1, j+1t, Si, jt, Si+1, j-1t, Si+1, j+1t, S-i, jt+1)。

由于该演化规则互补, 有: Si, jt-1=f( Si-1, j-1t, Si-1, j+1t, Si, jt, Si+1, j-1t, Si+1, j+1t, Si, jt+1)推出:S^t-1=F(S^t, S^t+1), 可逆性证毕。

本文采用96699669H可逆规则作为主CA的迭代规则, 文献[5]对可逆规则的选取进行了详细说明, 表1给出了前驱状态为 Si, jt-1=0时的可逆规则真值表, 当前驱状态为 Si, jt-1=1时真值表取反即可。

表1

Table 1

表1(Table 1)

表1 可逆规则表 Table 1 Reversible rule Si-1, j-1t, Si-2, j+1t, Si, jt, Si+1, j-1t, Si+2, j+1t Si, jt+1 Si-1, j-1t, Si-2, j+1t, Si, jt, Si+1, j-1t, Si+2, j+1t Si, jt+1 00000 1 10000 1 00001 0 10001 0 00010 0 10010 0 00011 1 10011 1 00100 0 10100 0 00101 1 10101 1 00110 1 10110 1 00111 0 10111 0 01000 0 11000 0 01001 1 11001 1 01010 1 11010 1 01011 0 11011 0 01100 1 11100 1 01101 0 11101 0 01110 0 11110 0 01111 1 11111 1

表1 可逆规则表 Table 1 Reversible rule

大多数应用于加密系统的细胞自动机一般为二态细胞自动机, 二态细胞自动机演化过程之中只有0, 1两个状态, 如何将灰度图像的0~255灰度值进行二态化就十分重要, 直接对图像进行二值化处理只会让图像损失部分信息, 即发生图像失真, 文献[4]提出了将图像分为8个位面图的思想, 每个位面图的信息只含有0和1。在此作简要说明:

I为图像的灰度值, mod为取余数运算, 高层位面到低层位面顺序为Layer8~Layer1,

Layer8=I/2⁷

Layer7=(I mod2⁷)/2⁶

Layer6=(I mod2⁶)/2⁵

Layer5=(I mod2⁵)/2⁴

Layer4=(I mod2⁴)/2³

Layer3=(I mod2³)/2²

Layer2=(I mod2²)/2¹

Layer1=(I mod2¹)/2⁰

由8个位面复原一副图像时, 只需将每个位面的数据乘以其权值即可还原图像。公式如下所示:

Image=Layer8* 2⁷+Layer7* 2⁶+Layer6* 2⁵+Layer5* 2⁴+Layer4* 2³+Layer3* 2²+Layer2* 2¹+Layer1

细胞自动机的边界条件是其迭代过程中不可缺少的环节, 常规的边界条件设置方法有边界补零, 和边界补1以及循环边界条件等方法, 边界条件设置的不同, 最终迭代结果也有显著差异。本文从提高密钥在加密系统中参与度的方面考虑, 提出了一种将密钥嵌入到细胞自动机边界条件的设计方法。

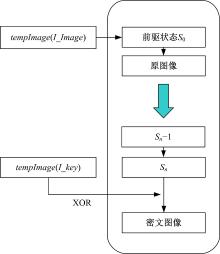
取密钥种子图像I_KEY, 行数为m, 列数为n, 使用混沌规则的细胞自动机对其进行迭代。取迭代结果的第n-1, n列作为左边界; 第1, 2列作为右边界; 第m-1, m行作为上边界, 第1, 2行为下边界, 其余四角空余位以0填充, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 密钥嵌入边界条件的示意图Fig.1 Key embedding boundary condition

受到文献[3]的尾数据与密钥进行异或运算的启发, 首先将密钥图像I_KEY分为8个位面, 分别与S_n对应的8个位面进行按位异或运算:

ScipN=S^NXOR key

式中:I_KEY为密钥种子图像, I_Image为明文图像, tempImage()函数代表混沌规则的细胞自动机的输出。S₀为初始迭代的前驱状态, 该状态由明文图像内容决定, 即以I_Image为种子, 由混沌行为的细胞自动机迭代n次得到尾数据S_n。随后将此数据与以I_KEY为种子产生的图像按位异或, 最终获得受密钥保护的密文信息, 具体过程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 密钥对尾数据进行保护Fig.2 Key protects tail data

单一对明文图像进行细胞自动机迭代的方法虽然简便, 却存在明文扩散性差的缺点, 仅仅依靠提高迭代次数的方法无疑增加了计算成本, 而且降低系统运行效率。考虑到计算效率的问题, 本文采用将历次迭代结果进行行列矩阵转置的方法来提高明文扩散性, 这种轻量级的转置运算对系统运行效率造成的影响较低, 同时也能达到置乱的目的, 转置运算的效果分析在实验部分有详细阐述。

该算法采用m× n的图像作密钥, 结合加密系统的五邻居细胞自动机规则选取, 因此其密钥空间巨大, 密钥空间公式为:

Keyspace= 225× 2^mn

式中:m, n为密钥图像行列数, 本文加密示例Lena图像仅为300* 300, 则其密钥空间高达2³²× 2^{300× 300}, 因此该算法可有效抵抗穷举攻击。

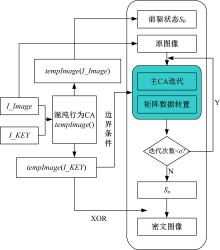
首先将待加密的明文图像I_Image, 和密钥种子图像I_KEY分为8个位面图, 输入具有混沌行为的一维二态四邻居细胞自动机tempImge(), 用以产生好的随机图像, 其中该细胞自动机采用9d62(hex)规则; 其次, 将输出的tempImge(I_Image)作为原图像的前驱状态, tempImge(I_KEY)嵌入主CA迭代的边界条件; 再次, 设主CA的迭代次数n, 每次迭代后的结果经过矩阵转置运算后再次进入CA迭代, 直到循环n次, 产生尾数据S_n; 最终, 尾数据S_n与前面已经生成的tempImge(I_KEY)进行按位异或运算得到密文图像。流程图如图3所示。解密是加密的逆过程, 此处不再赘述。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 整体加密算法流程图Fig.3 Flow chart of whole encryption algorithm

密钥混淆性统计的是密钥仅有一位变化, 按此密钥解密图像出错位数有多少; 图4为按照错误密钥解密的效果图, 这里的密钥仅有一位出错, 选取CA迭代次数n=100, 采用控制变量法, 以下各图仅CA邻居结构不同, 其他参数完全一致。根据以下图表可以发现, 偏X2型细胞自动机邻居结构下的解密出错位数明显高于其他情况, 即按偏X2型结构迭代的细胞自动机的密钥混淆性更好。故本文采用偏X2型邻居结构。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同邻居结构下的解密图Fig.4 Decryption graphs with different neighborhood structures

表2

Table 2

表2(Table 2)

表2 密钥混效率 Table 2 Mixing efficiency of key 邻居结构类型 Von Neumann X型 偏X1型 偏X2型 密钥混淆率/% 58.72 46.04 77.9 93.78

表2 密钥混效率 Table 2 Mixing efficiency of key

明文扩散性是指, 当原图像仅一位变化时, 加密后密文图像变化多少位, 加入转置运算后明文扩散性具有明显的提升, 密钥混淆性也有小幅度提升; 以偏X2型为例, 选取CA迭代次数n=100, 加密Lena图像, 混淆性比较如图5所示; 由于扩散性的比较是两个密文图像对照, 故只在表3中给出数据。

表3

Table 3

表3(Table 3)

表3 转置运算对混淆率和扩散性的影响 Table 3 Influence of transpose operations on aliasing and diffusivity 偏X2型结构 有转置运算时 无转置运算时 密钥混淆率/% 98.32 93.78 明文扩散性/% 60.62 24.48

表3 转置运算对混淆率和扩散性的影响 Table 3 Influence of transpose operations on aliasing and diffusivity

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 转置运算的影响Fig.5 Influence of transpose operation

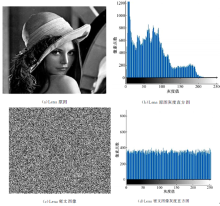
首先, 关注加密前后灰度直方图的变化, 对比效果如图6所示。评价加密算法的好坏一个重要的指标就是密文相关性大小, 对于图像而言, 有水平相关性, 垂直相关性, 和对角相关性。其次, 本文相关性指标如图7所示。如下公式中N为像素点数, E(x)为期望, D(x)为方差, r_xy为相关系数, cov(x, y)为协方差。

E(x)=1N∑i=1Nx(i)D(x)=1N∑i=1N[x-E(x)]2rxy=cov(x, y)D(x)D(y)cov(x, y)=1N∑i=1N[x(i)-E(x)][y(i)-E(y)]

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 加密前后图像以及灰度直方图Fig.6 Original image and gray histogram before and after encryption

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 相关性系列分析Fig.7 Correlation series analysis

表4

Table 4

表4(Table 4)

表4 相关性分析 Table 4 Correlation series analysis 图像参数 明文 密文 文献[5]密文 垂直相关度 0.9784 2.0406e-04 -8.9706e-004 水平相关度 0.9661 -3.0670e-05 0.0049 对角相关度 0.9786 0.0043 0.0027

表4 相关性分析 Table 4 Correlation series analysis

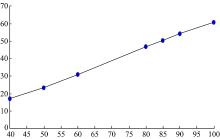
所谓雪崩效应是明文的扩散特性的一种程度:即明文中的任意一比特位发生变化时, 经过n次迭代得到密文中接近有一半的比特位发生变化, 密文中变化的比特位数越接近50%, 说明雪崩效应越明显。雪崩效应实质上反应了一种不稳定的平衡状态, 是衡量加密算法的重要指标。本文提出的算法的雪崩效应走势, 如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 雪崩效应走势图Fig.8 Avalanche effect chart

表5

Table 5

表5(Table 5)

表5 雪崩效应 Table 5 Avalanche effect 迭代次数 40 50 60 80 85 90 100 明文扩散率/% 18.1 23.26 30.76 46.67 50.24 54.08 60.62

表5 雪崩效应 Table 5 Avalanche effect