目标电磁散射特性对高分辨率星载SAR图像仿真影响

引用本文

康利鸿, 田菁, 孙希龙, 张晔. 目标电磁散射特性对高分辨率星载SAR图像仿真影响. 吉林大学学报（工学版）, 2017, 47(5): 1661-1668
KANG Li-hong, TIAN Jing, SUN Xi-long, ZHANG Ye. Influence of target electromagnetic scattering characteristics on high resolution space borne SAR image simulation. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1661-1668 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705044
Permissions

目标电磁散射特性对高分辨率星载SAR图像仿真影响

康利鸿^1,², 田菁², 孙希龙², 张晔¹

1.哈尔滨工业大学电子与信息工程学院,哈尔滨 150001

2.北京市遥感信息研究所,北京100192

作者简介:康利鸿(1974-),男,研究员,博士.研究方向:星载SAR应用总体.E-mail:gregrs@126.com

基金项目:“863”国家高技术研究发展计划项目(2015AA7013029)

摘要

建立了考虑目标电磁散射特性时频变化的回波仿真模型,给出了目标电磁散射特性对回波在方位向和距离向的调制效果,并对典型目标进行了回波仿真和成像处理,验证了目标电磁散射特性对高分辨率星载SAR图像仿真的影响,并提出了高分辨率星载SAR图像仿真方法改进的方向。

关键词: 雷达工程; 星载合成孔径雷达; 高分辨率; 仿真误差; 电磁散射特性

中图分类号:TN955 文献标志码:A 文章编号:1671-5497(2017)05-1661-08

Influence of target electromagnetic scattering characteristics on high resolution space borne SAR image simulation

KANG Li-hong^1,², TIAN Jing², SUN Xi-long², ZHANG Ye¹

1.School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001, China

2.Beijing Remote Sensing Information Institute, Beijing 100192, China

Abstract

The raw echo generation model is established considering the varying target electromagnetic scattering characteristics, and the module effects on azimuth and range direction are also presented. The echo generation and imaging results for typical target demonstrate the effectiveness of the proposed analysis method. Further improvement direction is put forward for the high resolution spaceborne SAR image simulation.

Key words: radar engineering; spaceborne synthetic aperture radar; high resolution; simulation error; electromagnetic scattering characteristic

Show Figures

0 引言

合成孔径雷达(SAR)系统具有全天时全天候成像的优点, 已成为现代遥感中不可或缺的重要手段。近年来, 我国SAR系统研究发展迅速, 在地形测绘、灾害监测、资源调查等诸多领域获得了广泛应用^{[1, 2, 3, 4]}。

星载SAR图像仿真是进行星载SAR系统设计和成像算法验证、SAR图像分析的有效手段^{[5, 6, 7]}。通常, 为了实现SAR信号与图像仿真, 都会对系统信号模型做一定程度的近似, 如计算目标后向散射系数(RCS)时, 一般采用SAR系统中心频点和正侧视情况下目标的RCS作为仿真输入^{[8, 9]}。在高分辨率情况下, 随着系统信号带宽的增大、合成孔径时间变长、前后斜视角变大, 采用中心频点和正侧视角度目标RCS作为输入, 必然会产生较大的图像模拟误差, 甚至在电磁散射特征上出现明显偏差, 对图像仿真的应用带来严重影响。近年来, 国内外一些学者已经开展了基于目标电磁散射计算的SAR仿真方法研究^{[10, 11, 12]}, 文献[10]中提出了利用弹射线法计算金属目标在不同频点和不同方位角度下电磁散射特性的回波仿真方法; 文献[11]中提出了利用并行时域有限差分方法进行SAR回波仿真的方法; 文献[12]提出了综合利用几何光学方法和全波电磁计算的方法进行大场景回波仿真的方法。但是以上研究中, 对于稳态散射中心假设在高分辨率情况下引入的仿真误差影响并未进行深入的分析和比较, 难以进一步支撑后续研究开展。

本文首先分析了典型目标RCS随频率和角度变化特性, 建立了考虑目标电磁散射特性变化的SAR回波信号模型, 从理论上分析了在SAR系统回波仿真时简化目标RCS模型带来的仿真误差, 然后以典型目标为例, 给出了典型高分辨率SAR系统参数情况下, 未考虑RCS随方位角和入射频率变化时计算得到的回波数据, 以及考虑RCS随方位角和入射频率变化时计算得到的回波数据, 进行了对比分析; 同时, 采用RD成像算法对上述两种回波数据进行成像处理, 分析了未考虑RCS随方位角和入射频率变化将会带来显著的SAR图像特征偏差, 验证了理论分析的正确性。最后, 给出了高分辨率SAR仿真方法的改进方向。

1 典型目标RCS特性

为了开展目标后向散射特性时变特性对高分辨率SAR图像仿真的影响, 首先对几种简单目标的RCS随方位角和频率变化的特性进行分析。

理想导电矩形薄板的RCS近似为:

$\begin{matrix} \begin{matrix} σ = \frac{4 π s^{2} h^{2}}{λ^{2}} {(cosθ)}^{2} \cdot \\ {(\frac{\sin (sksinθcosφ)}{sksinθcosφ} \frac{\sin (h k sinθcosφ)}{h ksinθcosφ})}^{2} \end{matrix} \end{matrix}$ （1）

式中:λ 为入射波长; s为平板短边; h为平板长边; θ 为视角; φ 为方位角, k=2π /λ 。

图1给出了理想导电矩形薄板在中心频点为9 GHz, 带宽为2 GHz、方位观测角度在± 9° 范围内, RCS随频率和视角的变化曲线。

	Figure Option View Download New Window
	图1 理想导电矩形薄板RCS随频率和方位角的变化Fig.1 RCS of ideal conductive rectangular plate changing with frequency and azimuth angle

理想导电三角形平板的RCS可近似为:

$\begin{matrix} \begin{matrix} σ = \frac{4 π A^{2}}{λ^{2}} {(cosθ)}^{2} \cdot \\ (\frac{[si n^{2} α - (\sin {(β / 2))}^{2}]^{2} + σ_{0}}{α^{2} - {(β / 2)}^{2}}) \end{matrix} \end{matrix}$ （2）

式中:a为三角形平板高度; b为三角形平板底长;

σ ₀=0.25(sin²φ · [(2a/b)cosφ sinβ -sinφ sin2α ]²; α =kasinθ cosφ ;

β =kbsinθ sinφ ;

A=ab/2。

图2给出了理想导电三角形平板在中心频点为9 GHz, 带宽为2 GHz、方位观测角度在± 9° 范围内, RCS随频率和视角的变化曲线。

	Figure Option View Download New Window
	图2 理想导电三角形平板RCS随频率与方位角变化Fig.2 RCS of ideal conductive triangular plate changing with frequency and azimuth angle

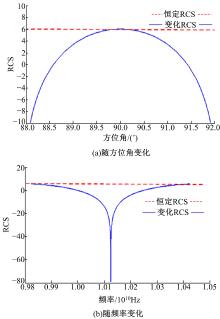
显然, 目标的RCS随方位角和频率发生显著变化, 仿真时若仅仅采用中心角度和中心频点处RCS, 必然会引入仿真图像失真。

随着目标结构复杂程度的增加, 目标RCS随角度和频率的变化会更剧烈, 如飞机进气口的腔型结构、舰船甲板以上的舰岛等。在这种情况下, 如仍采用单一角度和频点的简化目标RCS进行SAR仿真, 将会给仿真图像应用带来较大影响。

2 理论分析

将目标看作一个系统, 星载SAR系统发射信号经目标反射后被SAR接收, 目标的信号系统模型如图3所示。其中, s_t(t)为星载SAR系统发射的线性调频信号, γ (η , τ )为目标系统的系统响应, s_r(t)为SAR系统收到的回波信号。

	Figure Option View Download New Window
	图3 点目标信号与系统模型Fig.3 Signal and system model for point target

假设雷达发射如下形式的线性调频信号:

$\begin{matrix} s_{t} (τ) = rect (τ / T_{p}) \cos (2 π f_{c} τ + π k_{r} τ^{2}) (3) \end{matrix}$

式中:T_p为发射线性调频信号脉宽; f_c为线性调频信号中心频率; k_r为线性调频信号调频率。

当慢时刻为η 时刻, 回波信号可以写成如下形式:

$\begin{matrix} s (η, τ) = γ (η, τ) \otimes_{τ} g (η, τ) (4) \end{matrix}$

式中:g(η , τ )为系统对目标散射特性稳定为1的理想点目标的回波信号, 即:

$\begin{matrix} \begin{matrix} g (η, τ) = rect (η / T_{η}) rect [(τ - \frac{2 R (η)}{λ}) / T_{p}] \cdot \\ \exp (- j \frac{4 π}{λ} R_{0}) \exp (- j \frac{2 π v_{r}^{2}}{λ R_{0}} η^{2}) \cdot \\ \exp [jπ k_{r} {(τ - \frac{2 R (η)}{c})}^{2}] \end{matrix} \end{matrix}$ （5）

式中:T_η为合成孔径时间; R₀为中心斜距; R(η )为瞬时斜距; v_r为相对运动速度。

对于目标的散射特性γ (η , τ ), 传统的仿真方法往往采用稳态散射中心假设, 将其当做与入射波的频率和入射方向无关的常量来处理, 即令γ (η , τ )=σ 。

稳态散射中心假设不能反映目标散射特性在孔径和带宽内的变化, 对于低分辨星载SAR系统而言, 由于在合成孔径时间内雷达和目标的视线角变化不大, 且信号带宽也相对不大, 因此, 该假设对图像仿真的影响可以忽略。但是在高分辨率情况下, 在整个合成孔径时间内雷达与目标之间的视线角变化角度较大, 且SAR发射信号带宽也很大(达到几个GHz), 如果还将目标的RCS当作常数进行处理, 必将导致图像仿真失真。

一般地, 若目标散射特性函数γ (η , τ )的距离向频谱为γ (η , f_τ), 由式(4)可知:

$\begin{matrix} s (η, f_{τ}) = γ (η, f_{τ}) g (η, f_{τ}) (6) \end{matrix}$

将s(η , f_τ)进行方位向傅里叶变换就可得到回波信号的二维频谱s(f_η, f_τ):

$\begin{matrix} \begin{matrix} s (f_{η}, f_{τ}) = \\ \int_{-}^{\infty} γ (η, f_{τ}) g (η, f_{τ}) \exp (- j 2 π f_{η} η) dη = \\ γ (η, f_{τ}) \otimes_{f_{η}} γ (f_{η}, f_{τ}) \end{matrix} \end{matrix}$ （7）

由式(7)可知, 实际回波频谱为目标二维散射函数的频谱与理想点目标回波频谱关于方位频域的卷积。在SAR回波仿真中, 如果不考虑目标散射特性随方位角和带内频率的变换, 那么仅能得到g(f_η, f_τ)所示的部分信号, 其与真实回波信号s(f_η, f_τ)之间存在较大差异, 当采用二维匹配滤波进行成像后, 所得图像与真实图像之间偏差较大, 仿真精度不高。下面分距离向和方位向进一步分析。

2.1 距离向失真理论分析

对于距离向而言, s(η , τ )进行距离向匹配滤波的结果应该是g(η , τ )距离向匹配滤波结果与γ (η , τ )关于距离向快时间的卷积, 即:

$\begin{matrix} \begin{matrix} I_{s_r} = IF [s (f_{τ}) h_{r} (f_{τ})] = \\ IF [γ (f_{τ}) g (f_{τ}) h_{r} (f_{τ})] = γ (τ) \otimes_{τ} I_{g_r} \end{matrix} \end{matrix}$ （8）

式中:I_{s_r}为s(η , τ )成像结果的距离向剖面; h_r(f_τ)为距离向匹配滤波器的频域表示; I_{g_r}为g(η , τ )成像结果的距离向剖面。

以目标时延位置作为快时间0时刻, 则归一化后端I_{g_r}可近似表示成如下的sinc函数的形式:

$\begin{matrix} I_{g_r} = sinc (B_{τ} τ) = \frac{\sin (π B_{τ} τ)}{π B_{τ} τ} \end{matrix}$ （9）

式中:B_τ为发射信号带宽。

假设目标随频率的散射特性函数γ (f_τ)为:

$γ (f_{τ}) = \frac{B_{τ}}{4} - \frac{|f_{τ}|}{2}$ （10）

此时, 有

$I_{s_r} = IF [s (f_{τ}) h_{r} (f_{τ})] = IF [γ (f_{τ}) g (f_{τ}) h_{r} (f_{τ})] = IF \{(\frac{B_{τ}}{4} - \frac{|f_{τ}|}{2}) g (f_{τ}) h_{r} (f_{τ})\}$ （11）

其中, g $\begin{matrix} (f_{τ}) \end{matrix}$ 和h_r $\begin{matrix} (f_{τ}) \end{matrix}$ 可写为如下的形式:

$g (f_{τ}) = rect (\frac{f_{τ}}{B_{τ}}) \cdot \exp \{- j \frac{π f_{τ}^{2}}{k_{r}}\}$ （12）

$h_{r} (f_{τ}) = \exp \{j \frac{π f_{τ}^{2}}{k_{r}}\}$ (13)

需要注意的是, 式(12)中忽略了一些不影响后续分析的常数项。

将式(12)(13)代入式(11)得:

$\begin{matrix} \begin{matrix} I_{s_r} = IF \{(B_{τ} - \frac{|f_{τ}|}{2}) \cdot rect (\frac{f_{τ}}{B_{τ}}) \cdot \\ \exp \{- j \frac{π f_{τ}^{2}}{k_{r}}\} \cdot \exp \{j \frac{π f_{τ}^{2}}{k_{r}}\}\} = \\ IF \{rect (\frac{f_{τ}}{B_{τ}}) (\frac{B_{τ}}{4} - \frac{|f_{τ}|}{2})\} \end{matrix} \end{matrix}$ (14)

则I_{s_r}为:

$\begin{matrix} I_{s_r} = \frac{{[\sin (\frac{B_{τ}}{4} τ)]}^{2}}{τ^{2}} = {(\frac{B_{τ}}{4})}^{2} \frac{{[\sin (π \cdot \frac{B_{τ}}{4 π} τ)]}^{2}}{{(π \cdot \frac{B_{τ}}{4 π} τ)}^{2}} = {(\frac{B_{τ}}{4})}^{2} {[sinc (\frac{B_{τ}}{4 π} τ)]}^{2} \end{matrix}$ （15）

归一化后, I_{s_r}的形式如下:

$\begin{matrix} I_{s_r} = {[sinc (\frac{B_{τ}}{4 π} τ)]}^{2} \end{matrix}$ （16）

比较式(9)与式(16)可得:

$I_{s_r} = I_{g_r} \cdot Δ_{r} (τ)$ （17）

式中：

$\begin{matrix} Δ_{r} (τ) = {[sinc (\frac{B_{τ}}{4 π} τ)]}^{2} / sinc (B_{τ} τ) \end{matrix}$ (18)

即当仿真时未考虑目标散射特性随频率的变化特性时, 仿真得到的图像与真实图像间距离向信号差异。

2.2 方位向失真理论分析

对于方位向而言, s(η , τ )进行方位向匹配滤波的结果应该是g(f_η, τ )与γ (f_η, τ )卷积的匹配滤波器输出。

$\begin{matrix} I_{s_a} = IF \{[γ (f_{η}) \otimes_{η} g (f_{η})] \cdot h_{a} (f_{η})\} \end{matrix}$ (19)

式中:I_{s_a}为s(η , τ )成像结果的方位向剖面; h_a(f_η)为方位向匹配滤波器的频域表示。

假设γ (η )具有如下的一种特殊形式:

$\begin{matrix} γ (η) = rect (\frac{2 η}{η_{A}}) = \{\begin{matrix} 1, |η| \leq η_{A} / 4 \\ 0, else \end{matrix} \end{matrix}$ (20)

式中:η _A为合成孔径时间。

由式(19)可得图像的方位向剖面的具体形式如下:

$\begin{matrix} \begin{matrix} I_{s_a} = IF \{FT [γ (η) g (η)] \cdot h_{a} (f_{η})\} = \\ IF \{FT [rect (\frac{2 η}{η_{A}}) g (η)] \cdot h_{a} (f_{η})\} = \\ IF \{rect (\frac{2 f_{η}}{B_{a}}) g (f_{η}) \cdot h_{a} (f_{η})\} \end{matrix} \end{matrix}$ (21)

此时方位向的多普勒带宽为B_a/2, 仅为目标散射特性不随方位向视角变化时的一半。由式(21)可得到具体形式为:

$\begin{matrix} I_{s_a} = sinc (\frac{B_{a}}{2} η) \end{matrix}$ (22)

而当目标散射特性不随方位角变化时, 图像的方位向剖面I_{g_a}为如下的形式:

$I_{g_a} = IF \{[δ (f_{η}) \otimes_{η} g (f_{η})] \cdot h_{a} (f_{η})\} = IF \{g (f_{η}) \cdot h_{a} (f_{η})\} = sinc (B_{a} η)$ (23)

比较式(22)和式(23)可得:

$\begin{matrix} I_{s_a} = I_{g_a} \cdot Δ_{a} (η) (24) \end{matrix}$

式中:Δ _a(η )=sinc $\begin{matrix} (\frac{B_{a}}{2} η) \end{matrix}$ /sinc $\begin{matrix} (B_{a} η) \end{matrix}$ =1/cos(π $\begin{matrix} \frac{B_{a}}{2} \end{matrix}$ η ), 为仿真时未考虑目标散射特性随频率的变化特性时, 仿真得到的图像与真实图像间方位向信号差异。

如果目标的散射不是全向性的, 而是具有式(20)所示的这种特殊形式时, 方位向的图像的实际分辨率无法达到理论分辨率。

3 仿真验证与分析

为进一步验证前面的理论分析结果, 本文进行了典型时变后向散射特性目标的回波信号仿真, 进一步从仿真得到的数据上分析了目标电磁散射特性变化对图像的影响。

3.1 目标RCS变化仿真分析

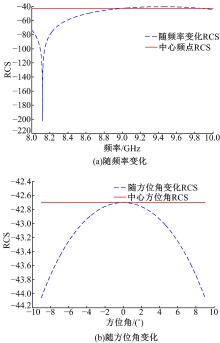
不失一般性, 考虑如图4所示的“ 哑铃状” 目标。仿真系统参数如下:方位向波束宽度为3.4° ; 信号带宽为700 MHz; 中心频率为10.124 GHz。

	Figure Option View Download New Window
	图4 “ 哑铃” 目标相对RCS几何关系Fig.4 RCS of “ dumbbell” target

计算得到上述仿真条件下目标RCS随方位角和频率的关系曲线分别如图5(a)(b)所示。

	Figure Option View Download New Window
	图5 目标RCS变化曲线Fig.5 Curve of target RCS changing

3.2 SAR回波数据与成像仿真分析

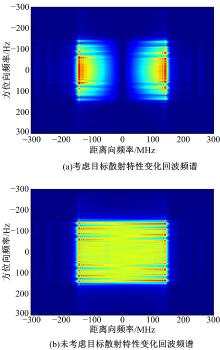
图6给出了理想点目标和考虑目标散射特性变化两种情况下的仿真回波数据, 图6(a)为考虑了目标散射特性变化的回波频谱, 图6(b)为未考虑目标散射特性变化的回波频谱。从图中可以明显看出散射特性变化对二维频谱的调制。

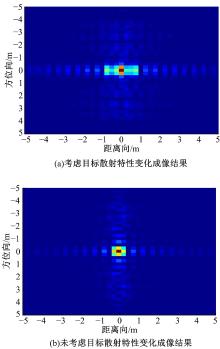
	Figure Option View Download New Window
	图6 回波频谱对比Fig.6 Comparison of echo frequency spectrum

利用RD算法, 对回波数据进行成像处理, 图7(a)和图7(b)分别给出了图6(a)和图6(b)两种情况下的成像结果。

	Figure Option View Download New Window
	图7 成像结果对比Fig.7 Comparison of image formulation results

	Figure Option View Download New Window
	图8 距离向频谱Fig.8 Frequency spectrum in range distance

从图7可见两种情况下成像结果间存在明显差异, 说明目标RCS空间变化特性和频率响应特性将在其SAR图像上直接体现。由于回波信号频谱受到了目标散射特性变化的调制, 两者的成像结果存在较大的差异, 下面根据成像结果分别对两者之间的方位向差异和距离向差异进行分析。

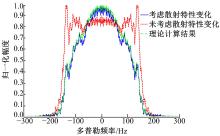
首先分析两种仿真中图像距离向剖面之间的差异。图8给出了距离向频谱, 实线是考虑散射特性变化时回波的距离向频谱, 虚线是未考虑散射特性变化时回波的距离向频谱。可见, 由于图5所示的频率响应函数γ (f_τ)的存在, 造成两者频谱间存在较大的差异。基于仿真中使用如图5所示的γ (f_τ), 通过式(8)计算得到的距离向频谱如图9所示, 可见理论计算结果与仿真中获得的实际频谱(图8中的实线)具有很高的吻合度。

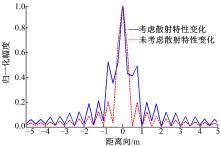
图10给出了两种仿真中成像结果的距离向剖面, 可以看出, 由于目标散射特性随频率变化的存在, 距离向聚焦结果与理想点目标聚焦结果存在较大的差异。图11给出了利用计算得到的距离向聚焦结果, 可见理论计算结果与图10中实线给出的实际仿真结果吻合较好。

	Figure Option View Download New Window
	图9 距离向频谱理论计算结果Fig.9 Frequency spectrum in azimuth distance

	Figure Option View Download New Window
	图10 图像距离向剖面Fig.10 Image profile in range distance

	Figure Option View Download New Window
	图11 距离向剖面理论计算结果Fig.11 Theoretical image profile in range distance

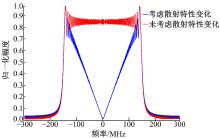
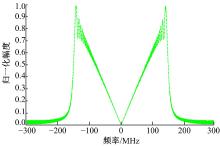
下面对方位向成像结果的差异进行说明。图12给出了方位向剖面的频谱, 其中, 实线为考虑散射特性变化时回波的方位向频谱, 虚线为未考虑散射变化时的方位向频率。从图12可以看出, 两者之间的频谱存在较大的差异, 根据前面的分析, 当考虑电磁散射特性变化时, 方位向频率应该等于电磁散射变化的方位向函数的频谱与理想点目标回波频谱的卷积。基于仿真中使用如图5所示的γ (f_τ), 计算得到回波方位向频率如图12中的点划线所示, 可以看出, 理论计算结果与仿真结果具有很高的吻合度。

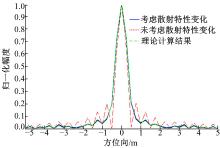
	Figure Option View Download New Window
	图12 方位向频谱Fig.12 Frequency spectrum in azimuth distance

图13给出了图像的方位向剖面, 考虑散射特性变化时的图像(实线)与未考虑散射特性变化时的图像(虚线)存在一定的差异, 主瓣有所展宽。图中的点划线是理论计算结果, 与实线所示的考虑散射特性变化时的方位向剖面具有很高的吻合度。

	Figure Option View Download New Window
	图13 图像方位向剖面Fig.13 Image profile in azimuth distance

从以上仿真结果可以看出, 采用目标“ 稳态散射假设” , 高分辨率SAR系统仿真忽略了目标后向散射特性的空间变化特性和频率响应特性, 将会产生失真, 一是出现方位向“ 球化” 效应, 即不考虑目标角度导致仿真图像中的目标会产生方位角旋转效应; 二是出现“ 尺寸频变” 效应, 即不考虑频率响应特性导致目标电尺寸不变而几何尺寸随频点变化。

4 结束语

采用目标“ 稳态散射假设” , 高分辨率SAR系统仿真忽略了目标后向散射特性的空间变化特性和频率响应特性, 将会产生失真, 主要是方位向“ 球化” 和“ 尺寸频变” 效应。为确保高分辨率情况下目标的SAR图像仿真能够准确反映目标特征, 后续应采用宽带电磁场数值算法计算目标在每个角度和每个频点上的RCS特性, 然后进行SAR系统仿真, 才能保证精度。可以采用时域有限差分方法等电磁场数值计算方法进行目标散射特性计算, 但这会带来极大的计算困难, 后续还需进一步研究降低计算量的方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	吴一戎, 朱敏慧. 合成孔径雷达技术的发展现状与趋势[J]. 遥感技术与应用, 2000, 15(2): 121-123. Wu Yi-rong, Zhu Min-hui. The developing status and trends of synthetic aperture radar[J]. Remote Sensing Technology and Application, 2000, 15(2): 121-123. [本文引用:1]
[2]	邓云凯, 赵凤军, 王宇. 星载SAR 技术的发展趋势及应用浅析[J]. 雷达学报, 2012, 1(1) : 1-10. Deng Yun-kai, Zhao Feng-jun, Wang Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1-10. [本文引用:1]
[3]	张雄美, 易昭湘, 田淞, 等. 结合形态学属性断面与支持向量机的合成孔径雷达图像变化检测[J]. 光学精密工程, 2014, 22(10): 2832-2839. Zhang Xiong-mei, Yi Zhao-xiang, Tian Song, et al. Change detection of SAR images using morphologic attribute profile and support vector machine[J]. Optics and Precision Engineering, 2014, 22(10): 2832-2839. [本文引用:1]
[4]	刘向增, 田铮, 史振广, 等. 基于FKICA-SIFT特征的合成孔径图像多尺度配准[J]. 光学精密工程, 2011, 19(9): 2186-2196. Liu Xiang-zeng, Tian Zheng, Shi Zhen-guang, et al. SAR image multi-scale registration based on FKICA-SIFT features[J]. Optics and Precision Engineering, 2011, 19(9): 2186-2196. [本文引用:1]
[5]	Smolarczyk M, Radar signal simulator for SAR algorithms tests[C]//Proceedings of International Radar Symposium, Germany, 2003: 509-513. [本文引用:1]
[6]	Chang Y L, Chiang C Y, Chen K S. SAR image simulation with application to target recognition[J]. Progress in Electromagnetics Research, 2011, 19: 35-57. [本文引用:1]
[7]	Zeng Tao, Hu Cheng, Sun Han-wei, et al. A novel rapid SAR simulator based on equivalent scatters for three-dimensional forest canopies[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(9): 5243-5255. [本文引用:1]
[8]	张月婷, 仇晓兰, 丁赤飚, 等. 高分辨率 SAR 图像桥梁目标仿真与特性分析[J]. 雷达学报, 2015, 4(1): 78-83. Zhang Yue-ting, Qiu Xiao-lan, Ding Chi-biao, et al. The simulation and characteristics analysis on high resolution SAR images of bridges[J]. Journal of Radars, 2015, 4(1): 78-83. [本文引用:1]
[9]	董纯柱, 胡利平, 朱国庆, 等. 地面车辆目标高质量SAR图像快速仿真方法[J]. 雷达学报, 2015, 4(3): 351-360. Dong Chun-zhu, Hu Li-ping, Zhu Guo-qing, et al. Efficient simulation method for high quality SAR images of complex ground vehicles[J]. Journal of Radars, 2015, 4(3): 351-360. [本文引用:1]
[10]	张锐, 洪峻, 明峰. 基于电磁散射的复杂目标SAR回波与图像仿真[J]. 电子与信息学报, 2010, 32(12): 2836-2841. Zhang Rui, Hong Jun, Ming Feng. SAR echo and image simulation of complex targets based on electromagnetic scattering[J]. Journal of Electronics & Information Technology, 2010, 32(12): 2836-2841. [本文引用:1]
[11]	Pan Xin, Kang Li-hong, Zou Bin, et al. High-resolution SAR signal simulation using parallel FDTD method[C]//IEEE International Geoscience and Remote Sensing Symposium, Quebec City, 2014: 409-493. [本文引用:1]
[12]	Kulpa K S, Samczynski P, Malanowski M, et al. An advanced SAR simulator of three-dimensional structures combining geometrical optics and full-wave electromagnetic methods[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 776-784. [本文引用:1]

2000

0.0

. 2000, 15(2):121-123

The developing status and trends of synthetic aperture radar

合成孔径雷达技术的发展现状与趋势

Wu Yi-rong , Zhu Min-hui.

吴一戎, 朱敏慧

(Institute of Electronics,The Chinese Academy of Sciences,Beijing100080)

The recent developing status both in china and abroad on synthetic aperture radar is reviewed in the er. The trends of synthetic aperture radar in the early of coming century are analyzed, that include: multi- ameter (multi-frequency, multi-polarization, multi-angle, etc.) synthetic aperture radar; interferometric synthetic aperture radar; spotlight SAR; interference and anti-interference of SAR; SAR constellation and technology of calibration.

对合成孔径雷达技术在国外的发展现状和发展趋势进行了归纳分析。对当前合成孔径雷达技术研究的热点:多参数(多频段、多极化和多视角) SAR系统、SAR干涉测量、聚束SAR、SAR的干扰和反干扰、定标技术及其应用等方面进行了讨论。最后介绍了我国在合成孔径雷达技术研究方面的工作进展。

... 近年来,我国SAR系统研究发展迅速,在地形测绘、灾害监测、资源调查等诸多领域获得了广泛应用^[1,2,3,4] ...

2012

0.0

. 2012, 1(1):1-10

Brief analysis on the development and application of spaceborne SAR

星载SAR 技术的发展趋势及应用浅析

Deng Yun-kai , Zhao Feng-jun , Wang Yu.

邓云凯, 赵凤军, 王宇

... 近年来,我国SAR系统研究发展迅速,在地形测绘、灾害监测、资源调查等诸多领域获得了广泛应用^[1,2,3,4] ...

2014

0.0

. 2014, 22(10):2832-2839 DOI:doi:10.3788/OPE.20142210.2832

Change detection of SAR images using morphologic attribute profile and support vector machine

结合形态学属性断面与支持向量机的合成孔径雷达图像变化检测

Zhang Xiong-mei , Yi Zhao-xiang , Tian Song

张雄美, 易昭湘, 田淞

针对传统合成孔径雷达 (SAR)图像变化检测方法存在误差大、检测率低等问题,提出了一种基于形态学属性断面(MAP)的SAR图像变化检测方法。该方法利用MAP算法提取差异图像的几何结构特征,构造深入描述图像结构化信息的特征向量空间;在利用阈值法对图像进行分割的基础上,引入偏移因子,实现训练样本的自动选取;最后, 用支持向量机(SVM)在多维特征空间中对图像进行变化类与非变化类的分类。实验结果显示:本文算法的检测结果优于基于高斯模型的KI阈值法 (GM_KI)、基于广义高斯模型的KI阈值法(GGM_KI)和大津法(Otsu)等3种阈值法的检测结果,Kappa系数保持在0.87以上;当峰值信噪比(PSNR)介于[29,44]dB时,抗噪性能指标保持在0.97以上。这些结果证明了文中方法的有效性和优越性。

... 近年来,我国SAR系统研究发展迅速,在地形测绘、灾害监测、资源调查等诸多领域获得了广泛应用^[1,2,3,4] ...

2011

0.0

. 2011, 19(9):2186-2196 DOI:doi:10.3788/OPE.20111909.2186

SAR image multi-scale registration based on FKICA-SIFT features

基于FKICA-SIFT特征的合成孔径图像多尺度配准

Liu Xiang-zeng , Tian Zheng , Shi Zhen-guang

刘向增, 田铮, 史振广

In order to realize automatic registration of a Synthetic Aperture Radar(SAR) image, an approach of image multi-scale registration based on affine invariant Fast Kernel Independent Component Analysis-Scale Invariant Feature Transform(FKICA-SIFT) features is presented. First, the affine invariant SIFT descriptors are constructed according to the Hessian matrix of feature points. The FKICA is used to extract the independent components of the affine invariant SIFT descriptors to obtain new descriptors (FKICA-SIFT). After filtering the input images by using Steerable pyramid, the new descriptors are used to match the feature points detected from the synthetic images of the band-pass sub-images in each layer. Finally, a coarse-to-fine procedure is adopted for gradual optimizing transformation parameters to achieve the multi-scale registration results. Experimental results show that the correct matching rate of proposed algorithm is more than 85% when the threshold is less than 0.7 and that is more than 90% when the threshold is less than 0.5. The registration accuracy of the proposed algorithm can achieve sub-pixel level and it is better than those of SIFT, PCA-SIFT, ICA-SIFT and SURF methods. It has been applied to accurate detection of the changes of the Tangjiashan waters before and after the Wenchuan earthquake, and obtained results meet the requirements of accurate registration for SAR images.

针对合成孔径(SAR)图像的配准,提出一种基于仿射不变快速核独立成分分析-尺度不变特征变换(FKICA-SIFT)的多尺度配准方法。首先,根据特征点的Hessian矩阵构建仿射不变SIFT描述子。接着,利用FKICA提取该描述子的独立成分得到新的描述子FKICA-SIFT。然后,利用该描述子对Steerable滤波后的各层带通合成子图像提取的特征点进行匹配。最后,采用由粗到细的匹配策略逐步优化变换参数,实现图像的多尺度精确配准。实验结果表明,对有较大仿射变化的SAR图像,当阈值小于0.7时,该方法的匹配正确率大于85%,阈值小于0.5时,匹配正确率可达90%以上,配准精度达到亚像素水平, 优于SIFT,PCA-SIFT,ICA-SIFT及SURF等相关方法。使用该方法准确地检测出了地震前后唐家山堰塞湖水域的变化情况,基本满足了SAR图像变换检测前精确配准的要求。

... 近年来,我国SAR系统研究发展迅速,在地形测绘、灾害监测、资源调查等诸多领域获得了广泛应用^[1,2,3,4] ...

2003

0.0

... 星载SAR图像仿真是进行星载SAR系统设计和成像算法验证、SAR图像分析的有效手段^[5,6,7] ...

2011

0.0

... 星载SAR图像仿真是进行星载SAR系统设计和成像算法验证、SAR图像分析的有效手段^[5,6,7] ...

2014

0.0

... 星载SAR图像仿真是进行星载SAR系统设计和成像算法验证、SAR图像分析的有效手段^[5,6,7] ...

2015

0.0

. 2015, 4(1):78-83 DOI:10.12000/JR14139

The simulation and characteristics analysis on high resolution SAR images of bridges

SAR 图像桥梁目标仿真与特性分析

Zhang Yue-ting , Qiu Xiao-lan , Ding Chi-biao

张月婷, 仇晓兰, 丁赤飚

① (Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China) ② (Key Laboratory of Spatial Information Processing and Application System Technology,Chinese Academy of Sciences, Beijing 100190, China)

An approach for simulation and analysis on the high resolution Synthetic Aperture Radar (SAR) images is provided and bridges are chosen for analysis. According to the principle of SAR, the Geometry Optics (GO) is employed to calculate the direct scatterings and multi-path scatterings of the bridge in this approach. In this study, the Sydney Bridge is chosen for analysis, and the Terra-SAR data with 1 m resolution is used. The results show that, the main properties of the bridge with the simulation and the real data are consistent, which tests the validity of the approach. Furthermore, according to the simulation process, the main scattering characteristics of the SAR image of the Sydney Bridge are interpreted. The experiments show that this approach can provide the main scattering characteristics of the target, and also show that it can be helpful for SAR images interpretations.

该文针对多径散射特征，给出了一种高分辨率SAR图像的仿真与特性分析方法，以桥梁目标为例开展了分析，该仿真方法从SAR工作原理出发，利用几何光学法计算和分析桥梁目标的单次散射情况和多径散射情况，并根据雷达工作原理和成像机理利用散射数据获得仿真SAR图像。文中选择了悉尼大桥为研究对象，利用分辨率为1 m的Terra-SAR数据开展了实验，仿真获得的SAR图像与实际SAR图像的主要散射特征一致，验证了方法的有效性；同时，根据仿真算法的分析过程，文中给出了悉尼大桥SAR图像主要散射特征的细节解释。实验表明，该方法能够有效获得目标的多径散射特征，同时能够有效辅助目标的SAR图像理解工作。

... 通常,为了实现SAR信号与图像仿真,都会对系统信号模型做一定程度的近似,如计算目标后向散射系数(RCS)时,一般采用SAR系统中心频点和正侧视情况下目标的RCS作为仿真输入^[8,9] ...

2015

0.0

. 2015, 4(3):351-360 DOI:doi:10.12000/JR15057

Efficient simulation method for high quality SAR images of complex ground vehicles

地面车辆目标高质量SAR图像快速仿真方法

Dong Chun-zhu , Hu Li-ping , Zhu Guo-qing

董纯柱, 胡利平, 朱国庆

Aiming at meeting the requirement of the amass high-quality SAR images needed by template-based ground target recognition engineering practice, a novel efficient SAR signal level simulation method is proposed. The electromagnetic scattering interaction mechanisms including coherent clutter of ground, multiple reflection and edge diffraction of vehicle, coupling-scattering between vehicle and ground are accurately estimated by utilizing an efficient ray-tracing technique. High quality SAR images are finally created through the SAR imaging procedure. Simulation results show that, the new method is feasible and effective.

为满足基于模板的SAR地面车辆目标识别对海量高质量模板图像的工程应用需求,该文提出了一种基于射线追踪技术的SAR信号级高效仿真方法.该方法通过构建地面车辆目标SAR仿真场景物理模型并利用射线追踪方法准确模拟SAR探测过程中电磁波与场景中目标与环境的作用机理,实现对地面环境的宽带相干杂波、表面粗糙的复杂目标的宽带电磁散射以及地面-目标间耦合散射的快速计算,并通过SAR成像处理和图像相似度评估确认形成高质量SAR模板图像.数值结果验证了该文方法的准确性和高效性.

2010

0.0

. 2010, 32(12):2836-2841

SAR echo and image simulation of complex targets based on electromagnetic scattering

基于电磁散射的复杂目标SAR回波与图像仿真

Zhang Rui , Hong Jun , Ming Feng.

张锐, 洪峻, 明峰

... 近年来,国内外一些学者已经开展了基于目标电磁散射计算的SAR仿真方法研究^[10,11,12],文献[10]中提出了利用弹射线法计算金属目标在不同频点和不同方位角度下电磁散射特性的回波仿真方法 ...

2014

0.0

2014

0.0