作者简介:王靖宇(1976-),男,副教授,博士.研究方向:汽车空气动力学.E-mail:wangjy@jlu.edu.cn
采用双向流固耦合的方法对汽车外后视镜扰流进行仿真分析,对主要的振动形式进行阐述,探究其振动的机理。首先,研究了刚性后视镜模型,得到后视镜的阻力系数 Cd和升力系数Cl,为流致振动的研究提供一个比较的基础,同时验证了仿真方案的可行性。再对流致振后视镜绕流进行数值模拟,研究流致振后视镜在不同来流速度下的振动特性,得到阻力和升力系数、振动的振幅、涡脱频率等参数随速度的变化趋势。结果表明:当涡脱频率与后视镜结构的固有频率接近时,可以引起后视镜强烈的振动,而且对振动强度的影响程度远远大于对风场强度的影响。
Based on fluid-solid interaction method, simulation analysis of the flow around the external rearview mirror was carried out to investigate the mechanism of fluid-induced vibration, and the main vibration forms were described. First, the rigid external rearview mirror model was investigated to get the drag coefficient Cd, and lift coefficient Cl, which provide a comparison basis for the study of fluid-induced vibration and verify the feasibility of the simulation program. Then, the flow around the external rearview mirror was simulated by numerical method to investigate the vibration characteristics of the mirror under different velocities. The changes of the drag and lift coefficients, vibration amplitude, frequency of vortex shedding and other parameters with the velocity were obtained. Results show that strong vibration of the mirror occurs when the vertex shedding frequency is approach to the structural natural frequency of the external rearview mirror, and the vibration strength is far greater than the impact strength of the wind.
汽车外后视镜外形属于钝体结构, 气流流经后视镜时, 在外壳边缘发生气流分离, 在背风区形成卷涡, 随着涡的不断形成和脱落, 整个后视镜结构承受的气动力不断发生变化, 导致后视镜产生气动振动, 严重影响汽车舒适性及行驶安全性。
本文选取单个后视镜进行流动及结构振动的流固耦合数值模拟。单后视镜外形简单, 周围流场不会受到其他物体干扰, 便于探究流致振动的规律及深入探讨流致振机理, 可以作为整车模型的基础, 为寻求整车行驶时后视镜振动的控制方法提供基础。
许多学者在后视镜扰流方面已经做了一些研究, 文献[1, 2]通过试验研究, 分析了后视镜的振动特性。李启良等[3]通过数值模拟和实验研究研究了汽车后视镜的流场特性。杨博等[4]采用计算流体力学软件Star-CD和稳态那维尔-斯托克斯方法, 获得后视镜区域流场特性。Homsi和Narain[5]进行了后视镜的稳态和瞬态数值计算, 结果表明, 后视镜后面形成的涡脱落现象是造成气动力波动的主要原因。Xiong等[6]使用单向流固耦合方法研究了后视镜振动问题, 证明了频率为0~100 Hz时容易使后视镜发生共振。Watkins[7]主要研究了后视镜在气动力激励下的旋转振动, 认为后视镜的振动是由于周围流场的变化导致后视镜外壳振动。在过去的汽车后视镜外流场研究中, 关于后视镜流固耦合的研究内容较少, 已有的研究也多是集中于试验研究和单向耦合仿真。试验研究成本大, 耗时长且不能深入地探讨振动机理; 单向耦合只是把流体计算结果作为固体计算的初值, 不能很好地反映流体与固体相互作用的过程。
针对以上研究的不足, 本文采用双向弱耦合的数值解法, 采用有限体积法离散求解任意拉格朗日-欧拉描述下的不可压缩N-S方程, 结构部分采用有限元法求解弹性动力学方程求解, 进行后视镜双向流固耦合的三维流场和结构的数值模拟, 同时对比无耦合仿真(CFD)和有耦合仿真(FSI), 研究了车速变化对后视镜振动特性的影响规律。
假设空气为不可压牛顿流体, 后视镜绕流模拟过程中的控制方程为非定常雷诺平均N-S方程[8], 其无量纲形式的表达式为:
式中:Q为守恒向量变量; Fi、Gi、Hi为对流项通量向量; Fv、Gv、Hv为黏性项通量向量。流场部分通过star-ccm+进行模拟。
后视镜结构部分考虑流体的作用, 结构动力响应由以下运动方程描述:
式中:
数值计算中, 通常流体运动和结构运动的描述方式不同, 固体力学中通常采用拉格朗日坐标系, 在于描述物质点的运动; 流体力学中通常采用欧拉坐标系, 在于描述空间点的状态。任意拉格朗日-欧拉(Arbitrary Lagrange-Euler, ALE)法综合了拉格朗日方法和欧拉方法的优势, 通过引入参考域, 解决了流固耦合求解中因坐标系不统一而引起的流固运动界面不协调的问题。
在ALE方法中, 引入了除拉格朗日和欧拉坐标系以外的第3个坐标系, 与参考坐标相关的材料微商可以用式(3)描述:
式中:Xi为拉格朗日坐标; xi为欧拉坐标; wi为相对速度。
假设
(1)质量守恒方程为:
(2)动量守恒方程
控制流体流动的方程式N-S方程的ALE描述如式(5)所示:
式中:
式中:p为压强; μ 为流体动力黏性系数; δ ij为乘积函数。
(3)能量守恒方程为:
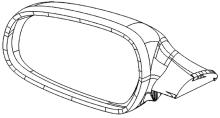
首先对刚性后视镜进行数值模拟和分析, 采用的后视镜模型为DrivAer整车外后视镜, 如图1所示。
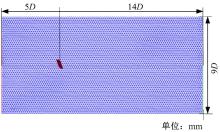
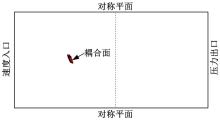
计算域大小的确定原则是确保阻塞比小于5%, 同时保证在后视镜存在振动位移时也能满足此要求。后视镜垂直于流向的展向长度分别为234 mm和138.62 mm, 取较大值作为后视镜特征长度D=234 mm。将得到的几何模型在Hypermesh中几何清理。建立如图2所示的计算域, 入口、出口距离后视镜分别为5D、14D; 沿特征长度方向取为9D; 计算域高度取为7倍后视镜高度。这样得到的计算域阻塞比为1.13%, 满足要求。计算域上下表面为滑移壁面, 与展向垂直的面为对称平面, 采用速度入口和压力出口。
本文计算域表面网格大小为50 mm, 后视镜表面网格为2 mm。为了捕捉这些流动特征, 采用如图3所示的3个加密区, 加密区尺寸分别为8、20和30 mm, 采用多面体网格, 体网格总数为166万。
考虑到汽车是在额定风速下运行, 汽车后视镜外部存在着分离、剪切等复杂的流动现象, 因此计算湍流模型采用具有层流-湍流转捩修正的SST k-ω 湍流模型, 该模型在近壁面区域有更好的计算精度和算法稳定性[9]。
本文共计算不同雷诺数下固定后视镜9个工况, 计算中监测阻力系数和升力系数的变化, 之后计算得到斯特罗哈数。计算得到对应车速下的升力系数Cl的均方根值Clrms、最大值Clmax、最小值Clmin和阻力系数Cd的平均值Cdmean、最大值Cdmax、最小值Cdmin, 如表1所示。
| 表1 不同车速下外后视镜动力系数 Table 1 Dynamic coefficient of external rearview mirror under different velocities |
由阻力系数平均值可以看出, 在低速时阻力系数处于不平稳状态, 存在小幅度的波动, 当速度大于70 km/h时, 阻力系数趋于稳定。这样的规律从升力系数的均方根值变化中也可以看出。
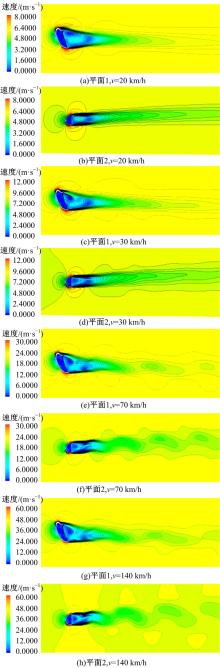
为了观察后视镜尾流区域流场的结构, 沿后视镜几何中心作水平平面1、垂直平面2。在本次仿真中, 得到的不同截面上二维速度标量如图4所示。
当速度低于30 km/h时, 平面1和2均未出现规则的漩涡脱落现象。所以此速度下未发生周期性脱落的漩涡, 这使得升力的变化规律不唯一。当车速大于70 km/h时, 以图示速度为例, 在水平截面内观察到了规则的漩涡脱落, 而且在尾流区脱落漩涡的外围形成了第二层漩涡, 同时随着内部漩涡的脱落也向后脱落, 在垂直截面内也观察到了相同的现象。
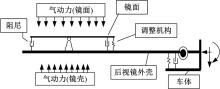
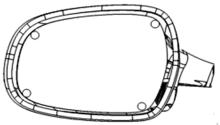
在实际情况中, 流体和固体是一个相互作用的过程, 本文将固体赋予可变的边界条件, 从空气动力学的角度探究流致振的发生机理及影响规律。在本文研究中, 考虑到后视镜内部几何结构对流场干扰较小, 只对后视镜镜面的运动产生影响。因此简化后视镜内部几何构造, 对后视镜的运动连接使用等效单元代替。简化模型如图5所示。
在工程实际中, 后视镜在每一个自由度方向的振动都受到刚度和阻尼的影响。因此, 在后视镜有限元模型中应赋予材料刚度和阻尼特性。本文设置的后视镜的两个刚度属性分别如下:球副为16 640(N· mm/rad), 转动副为959 000(N· mm/rad), 阻尼比为0.005[10]。因简化了后视镜内部结构, 质量相应减小。因此, 在后视镜总成质心处附加集中质量点, 得到的总质量为1.09 kg, 保证质量与实际后视镜一致。
流致振后视镜模拟时采用与刚性后视镜相同大小的计算域, 入口和出口条件分别为速度入口和压力出口, 上下壁面为对称平面, 镜壳和镜面内外表面为流固耦合面, 如图6所示。
采用star-ccm+计算流场, Abaqus计算固体变形, 通过star-ccm+协同仿真平台实现数据的实时交换。在Abaqus软件中建立有限元模型, 参数如前文所述, 使用线性摄动分析步中的Lanczos求解器计算模型前10阶模态, 如表2所示。
由表2可以看出, 后视镜3阶模态以后模态频率已经超出了气流激励频率的范围, 因此有效模态只取前3阶进行分析。
| 表2 后视镜模态分布 Table 2 Modal distribution of external rearview mirror |
研究后视镜流致振数值模拟, 计算工况车速
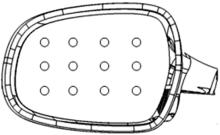
其中位移监测点取镜面边缘4个端点处, 如图7所示。压力系数监测点取镜面等间距12个, 通过压力系数反映表面压力分布, 如图8所示。
定量分析不同速度下后视镜振动的区别。其中, fs为刚性后视镜漩涡脱落频率;
| 表3 后视镜在不同车速下的振动参数 Table 3 Vibration parameters of external rearview mirror under different vehicle speed |
表3中分别得到了不同速度下后视镜钢化计算和涡激振计算唯一的漩涡脱落频率。由结果可知, 后视镜固定与振动时得到的涡脱频率基本接近, 但是存在微小的偏差, 后视镜固定时漩涡的脱落频率较小。
当v=20 km/h时, 中高频振幅大约为低频和高频的2倍, 低频振动频率与涡脱频率接近, 可见此频率振动由漩涡脱落引起; 当v=30 km/h时, 涡脱频率与位移频率相互错开, 可见此时没有产生强烈涡激现象; 当v=70 km/h时, 涡脱频率与中频振动基本接近, 但此时的频率相对于后视镜结构的固有频率差值较大, 因此涡激现象没有对振动产生很强烈的作用; 当80 km/h≤ v≤ 160 km/h时, 随着涡脱频率的不断增大, 致使其与结构的固有频率的差值也不断增加, 后视镜结构振动频率锁定在两个固定频率不再发生变化, 而且振动强度也呈现接近倍数的增长, 说明此时漩涡的脱落影响较小, 振幅只随着风场的强度增大而增加; 当v=180 km/h时, 此时低频振动频率发生了微弱的变化, 但是此时振幅却没有随着车速的增大而有明显的增加, 低频振幅反而减小, 说明此时风场强度特性的影响开始减小。
对后视镜振动的影响除升力和阻力外, 表面压力分布对气动特性同样有重要的影响。表面压力分布可用压力系数
式中:p0为大气压强; ρ 为空气密度; v∞ 为来流速度。
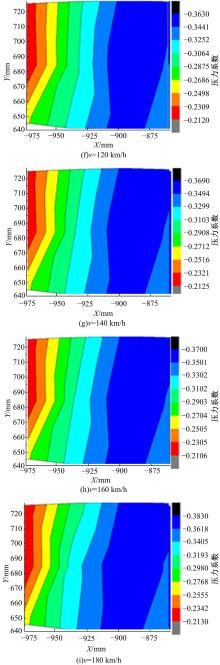
表面压力分布可以反应附面层的分离点以及转捩点, 压力分布可以间接通过压力系数来获得。由计算获得的压力系数做出镜面压力系数分布云图如图9所示。从图9可以看出, 各速度下镜面表面压力均为负值, 说明气流在镜壳边缘分离后没有再附着。而且所有速度下得到的表面压力分布规律出现一致性, 在镜面靠近车体侧压力较小, 沿着镜面展向逐渐增大, 在镜面最外端上方到达最大值。在表面压力的逐渐变化过程中, 就形成了使后视镜镜面趋于失稳的压差力。
由图9可知, 在低速时压差较小, 此时风场作用力不强烈; 随着风速的增大, 压差逐渐增大, 风场的作用力也变得强烈。因此通过表面压力证明了当涡脱频率大于固有频率时, 随着风速的增大, 风场强度对后视镜振动起主导作用。
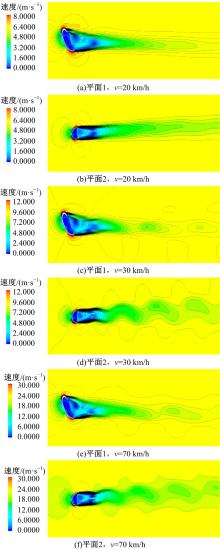
取与钢化后视镜相同的截面, 得到的流致振后视镜不同截面上二维速度标量如图10所示。
通过观察垂直截面的涡结构, 可以看出:随着速度的不断增大, 漩涡完全脱落的位置在不断地向后视镜方向移动, 导致这种现象的原因为流场速度不断增强, 因此漩涡的能量可以很快增大, 从而产生脱落。而且外层漩涡与内层漩涡的分界随着速度的增大也越来越明显, 外层漩涡从包络变为了与内层并列的漩涡。
(1)当涡脱频率与后视镜结构的固有频率接近时, 可以引起后视镜强烈的振动, 而且对振动强度的影响程度远远大于对风场强度的影响。
(2)各速度下后视镜表面存在相同的表面压力分布, 压力差导致后视镜失稳, 涡脱频率大于后视镜固有频率时, 随着风速的增大, 风场强度对后视镜振动起主导作用。
(3)随着速度的不断增大, 漩涡完全脱落的位置在不断地向后视镜方向移动。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|