基于液力缓速器换挡控制的半挂汽车列车制动稳定性

引用本文

何仁, 陈珊珊. 基于液力缓速器换挡控制的半挂汽车列车制动稳定性[J].吉林大学学报（工学版）, 2017,47(6): 1677-1687
HE Ren, CHEN Shan-shan. Braking stability of tractor-semitrailer based on gear-shifting strategy of hydraulic retarder[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1677-1687 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706002
Permissions

基于液力缓速器换挡控制的半挂汽车列车制动稳定性

何仁, 陈珊珊

江苏大学汽车与交通工程学院,江苏镇江 212013

作者简介:何仁(1962-),男,教授,博士生导师.研究方向:汽车机电一体化技术.E-mail:heren@ujs.edu.cn

基金:国家自然科学基金项目(51275212); 总装备部军内科研项目

摘要

针对液力缓速器改变半挂汽车列车车轮制动力分配会影响制动稳定性的问题,提出了一种液力缓速器换挡控制策略。根据牵引车后轴车轮与半挂车车轮的转速关系,对液力缓速器工作挡位进行主动调控。以半挂汽车列车车轮最佳抱死顺序为控制目标,采用Matlab/Stateflow设计换挡控制策略,并与半挂汽车列车整车动力学Matlab/Simulink模型联合仿真,分别模拟直线制动车轮抱死情况和直线制动受侧向力时的横向运动情况。仿真结果表明:本文换挡控制策略能使半挂汽车列车保持最佳抱死顺序,减小在部分路面上的制动距离,并且提高汽车列车直线行驶制动受侧向力作用时的横向稳定性。

关键词: 车辆工程; 液力缓速器; 换挡控制策略; 半挂汽车列车; 制动稳定性

中图分类号:U461.3 文献标志码:A 文章编号:1671-5497(2017)06-1677-11

Braking stability of tractor-semitrailer based on gear-shifting strategy of hydraulic retarder

HE Ren, CHEN Shan-shan

School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China

Abstract

The hydraulic retarder may change the distribution ratio the braking power of the tractor-semitrailer that negatively affects the braking stability. To solve this problem, a gear-shifting strategy of the hydraulic retarder is proposed. The strategy is designed to actively change the gear of the hydraulic retarder based on the relationship between the rear wheel of the tractor and the wheel of the semitrailer. With goal to optimize the locking sequence of the tractor-semitrailer, the Matlab/Stateflow is applied to design the gear-shifting strategy. Then this strategy is associated with the dynamic model of the tractor-semitrailer built with Matlab/Simulink to study the braking sequence during straight braking and the lateral motion during straight braking with lateral force. Simulation results show that the proposed strategy can help keep the optimum braking sequence, decrease the braking distance on the road with particular tire-road adhesion and improve the lateral stability of the tractor-semitrailer.

Keyword: vehicle engineering; hydraulic retarder; gear-shifting strategy; tractor-semitrailer; braking stability

Show Figures

0 引言

为了提高制动安全性和可靠性, 《机动车安全运行技术条件》^[1]中指出, 总质量大于等于12 000 kg的货车和专用作业车、危险货物运输车, 应装备缓速器或其他辅助制动装置。但是在半挂汽车列车上装配液力缓速器后, 牵引车后轴车轮所受制动力矩是液力缓速器与摩擦制动器制动力矩的叠加。由于液力缓速器制动力矩与传动轴转速的平方成正比, 半挂汽车列车各轮制动力之比在制动过程中是不断变化的, 导致车轮抱死顺序发生改变。如果牵引车后轮先抱死, 半挂汽车列车就可能会发生折叠失稳。迄今为止, 研究汽车列车制动稳定性的文献很多。文献^[2]提出了一种基于滑移率的制动力分配算法, 根据牵引车前轮滑移率控制牵引车后轮和半挂车车轮滑移率, 保证牵引车前轮先抱死, 以提高车辆的制动稳定性。文献^[3]根据牵引车的实际横摆角速度与目标值之间的误差, 实施主动制动, 可预防半挂汽车列车在低附着路面上发生折叠。另外, 针对装备有缓速器的单体车制动问题的研究也取得了丰富的成果。文献[4]建立了装备有缓速器的单体汽车的制动力与广义I曲线匹配的定性和定量评价法来评价制动稳定性。文献^[5]提出了将电涡流缓速器输出的制动力矩进行调节并加载在单体车后轮的方法, 改善了车辆的制动稳定性。文献^[6]提出安装缓速器的单体车辆需要重新调整制动力分配比。但是在现有研究中, 针对半挂汽车列车装备缓速器带来的制动稳定性问题的研究相对较少。文献^[7]提出一种通过控制器使半挂车预先制动, 从而实现牵引车和半挂车联合辅助制动的设计方案。文献^[8]指出威伯科研发的产品EBS会优先采用缓速器给牵引车后轴提供制动力, 减少牵引车后轴摩擦制动器摩擦片的磨损, 同时EBS系统会调节制动气室的压力, 使车轮滑移率保持最佳。在国外, 汽车列车上早已安装EBS系统, 但是EBS价格昂贵, 国内汽车列车鲜有安装, 且由于WABCO, KONRR等企业实行技术封锁, 无法获得EBS系统中相关的核心技术。

为此, 为了在提高半挂汽车列车的制动稳定性的同时降低产品成本, 本文拟利用一种新的液力缓速器换挡策略帮助半挂汽车列车在制动过程中实现最佳抱死顺序, 以提高半挂汽车列车的制动性能。

1 整车模型

1.1 半挂汽车列车运动模型

半挂汽车列车的结构参数如表1所示。半挂汽车列车在水平、干燥、硬实的路面上满载制动, 忽略空气阻力, 转向盘转角取0, 只考虑车辆行驶方向速度变化; 将牵引车多驱动轴和半挂车多轴各简化成一根轴, 且地面作用于车轮的法向力经过车轴中心。

(1)整车纵向动力学方程

$\begin{matrix} (m_{1} + m_{2}) \overset{\cdot}{v} = F_{x 1} + F_{x 2} + F_{x 3} (1) \end{matrix}$

式中: $\begin{matrix} v \end{matrix}$ 为整车纵向速度, m/s; F_x₁为牵引车前轴地面制动力, N; F_x₂为牵引车后轴地面制动力, N; F_x₃为半挂车车轴地面制动力, N。

(2)车轮转动动力学方程

$J_{1} {\overset{\cdot}{ω}}_{1} = - F_{x 1} R - T_{b 1} (2)$

$J_{2} {\overset{\cdot}{ω}}_{2} = - F_{x 2} R - T_{b 2} - T_{r} (3)$

$J_{3} {\overset{\cdot}{ω}}_{3} = - F_{x 3} R - T_{b 3} (4)$

式中:ω ₁为牵引车前轮转速, rad/s; ω ₂为牵引车后轮转速, rad/s; ω ₃为半挂车车轮转速, rad/s; J₁、J₂分别为牵引车前轮和后轮的转动惯量, kg· m²; J₃为半挂车车轮转动惯量, kg· m²; T_b1、T_b2分别为牵引车前轮和后轮制动器的制动力矩, N; T_b3为半挂车车轮制动器的制动力矩, N; T_r为液力缓速器作用在车轮上的制动力矩, N· m。

(3)车轮垂直载荷

轮胎的垂直载荷由静态载荷和动态载荷组成, 其中动态载荷由车辆在纵向加速度引起的。轮胎的垂直载荷可表示为:

$F_{z 1} = \frac{m_{1} g (l_{1} - \frac{\overset{\cdot}{v}}{g} h_{1})}{l_{1}} + [m_{2} g (l_{5} - l_{4} - \frac{\overset{\cdot}{v}}{g} h_{3}) (l_{1} - \frac{\overset{\cdot}{v}}{g} h_{2})] \times {[l_{3} (l_{5} - \frac{\overset{\cdot}{v}}{g} h_{2})]}^{- 1} (5)$

$F_{z 2} = \frac{m_{1} g (l_{3} - l_{2} + \frac{\overset{\cdot}{v}}{g} h_{1})}{l_{3}} + [m_{2} g (l_{5} - l_{4} - \frac{\overset{\cdot}{v}}{g} h_{3}) (l_{3} - l_{1} + \frac{\overset{\cdot}{v}}{g} h_{2})] \times {[l_{3} (l_{5} - \frac{\overset{\cdot}{v}}{g} h_{2})]}^{- 1} (6)$

$F_{z 3} = \frac{m_{2} g [l_{4} + \frac{\overset{\cdot}{v}}{g} (h_{3} - h_{2})]}{l_{5} - \frac{\overset{\cdot}{v}}{g} h_{2}} (7)$

式中: $\begin{matrix} F_{z 1} 、 F_{z 2} \end{matrix}$ 分别为牵引车前轴和后轴的垂直载荷, N; $\begin{matrix} F_{z 3} \end{matrix}$ 为半挂车车垂直载荷, N。

表1 半挂汽车列车参数 Table 1 Parameters of tractor-semitrailer

1.2 轮胎模型

采用基于双指数模型的纵向附着系数计算模型^[9]:

$μ = A [\exp (- bs) - \exp (- as)] (8)$

式中：

$a_{k + 1} = \frac{1}{S_{xm}} \ln \frac{(μ_{xp} / μ_{xs} - S_{xm}) a_{k} - 1}{μ_{xp} / μ_{xs} - 1}$

$A = \frac{μ_{xs}}{1 - aexp (- a S_{xm})}$

$b = - \ln [1 - aexp (- a S_{xm})]$

根据式(8)对a进行迭代求解时, 当 $\begin{matrix} a |\frac{a_{k + 1} - a_{k}}{a_{k}}| \leq e = 10^{- 3} \end{matrix}$ 停止迭代, 令 $\begin{matrix} a = a_{k + 1} 。 \end{matrix}$ 其中, 各种道路工况及行驶条件下路面附着特征参数的公式为:

$μ_{xp} = 0.92 \times 0 . 1304^{σ} + 0.002 \times e^{σ} (64 - v) - 0.0426 u (9)$

$μ_{xs} = 0.677 \times 0 . 1553^{σ} + 0.002 \times e^{σ} (64 - v) - 0.0426 u (10)$

$S_{xm} = 0.1532 σ^{3} - 0.47801 σ^{2} + 0.256 σ + 0.01693 + 0.105 \lg (64 / v) (11)$

式中:μ _x_p为峰值附着系数; S_x_m为峰值附着系数对应的车轮滑移率; μ _x_s为车轮完全滑移时路面附着系数; $\begin{matrix} u \end{matrix}$ 为车轮载荷系数, u=F_z/F_s, F_s为轮胎的标定载荷, N; $\begin{matrix} σ \end{matrix}$ 为路面状况的附着特征影响因子对各种路面的路况因子的分配。

1.3 主制动器模型

由于半挂汽车列车气压制动管路较长, 摩擦制动器制动力矩响应存在时间延迟, 因此将制动力增长时间作为气压制动响应延迟的输入因素, 可表示为:

$\begin{matrix} P_{mt} = \frac{1}{τs + 1} P_{mu} (12) \end{matrix}$

式中:P_mt为制动气室压力, MPa; $\begin{matrix} τ \end{matrix}$ 为制动力增长时间, s; P_mu为目标制动压力, MPa; $\begin{matrix} s \end{matrix}$ 为车轮滑移率。

凸轮型鼓式制动器制动力矩可表示为^[10]:

$\begin{matrix} T_{b} = P_{mt} A_{0} l_{SAL} B_{f} (13) \end{matrix}$

式中:T_b为制动力矩, N· m; B_f为制动鼓的制动因数; $\begin{matrix} A_{0} \end{matrix}$ 为制动缸作用面积, m²; $\begin{matrix} l_{SAL} \end{matrix}$ 为调整机构有效长度, m。

1.4 液力缓速器模型

半挂汽车列车采用某款液力缓速器。该液力缓速器分为5挡, 分别是恒速挡、一挡、二挡、三挡和四挡, 其中液力缓速器的一挡~四挡的充液率分别为25%、50%、75%、100%。该液力缓速器能提供的最大制动力矩为4000 N· m, 制动转矩 $\begin{matrix} T_{zh} \end{matrix}$ 与转子转速和充液率的关系^[11]为:

$\begin{matrix} \begin{matrix} T_{zh} = 745.83 {(\frac{n_{r}}{1000})}^{2} q_{c} - 12.32 (\frac{n_{r}}{1000}) q_{c} + \\ 11.8274 q_{c} + 7.54 (14) \end{matrix} \end{matrix}$

式中:n_r为转子转速, r/min; q_c为充液率。

2 摩擦制动器制动力分配系数优化

文献[12]以曲线 $\begin{matrix} φ_{j} - z \end{matrix}$ 与直线 $\begin{matrix} φ - z \end{matrix}$ 在对应制动强度下的两曲线之差的均方根最小为控制目标, 最佳抱死顺序为约束条件对半挂汽车列车的制动器制动力固定分配系数进行优化, 但是没有考虑联合国欧洲经济委员会汽车法规(ECE法规)^[14]中对牵引车和半挂车制动协调性的要求, 下面将把此要求作为优化约束条件之一, 对分配系数进行优化。

2.1 设计变量

待优化参数是制动器制动力分配系数β ₁ 、β ₂ 、β ₃, 三者满足关系:β ₁+β ₂+β ₃=1。本文仅考虑半挂汽车列车满载时的制动器制动力分配情况。

2.2 目标函数

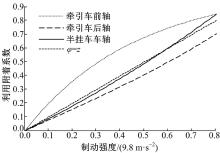
当各轮利用附着系数曲线φ _j-z接近于直线φ -z时, 整车制动效能最佳, 因此, 可用曲线与直线在对应制动强度下的两曲线之差的均方根最小作为目标函数:

$\begin{matrix} F (x) = \sqrt[]{\overset{3}{\sum_{i = 1}} \overset{16}{\sum_{j = 1}} (φ_{ij} - z_{j})^{2}} (15) \end{matrix}$

式中: $\begin{matrix} z_{j} = 0.05 j, j = 1, 2, \dots, 16 。 \end{matrix}$

2.3 约束条件

对于半挂汽车列车而言, 不同车轮抱死顺序将带来不同的制动安全问题。牵引车前轮先抱死时, 汽车将失去转向能力, 如果受到侧向力干扰, 汽车可能出现跑偏, 但是可通过操纵制动踏板及加速等方式恢复转向性能; 牵引车后轮先抱死时, 可能出现折叠现象, 此时车辆无法恢复稳定行驶状态, 处于危险工况; 半挂车车轮先抱死时, 可能出现甩尾现象, 但是也可通过操纵制动踏板及加速等方式恢复稳定行驶状态。根据车辆制动时的可控制性, 以上3种情况的危险程度由高到低依次为折叠、甩尾和失去转向能力。因此当车轮无法同时抱死时, 理想的抱死顺序为牵引车前轮、半挂车车轮和牵引车后轮^[13], 要使半挂车得到最佳抱死顺序, 约束条件可写为^[12]:

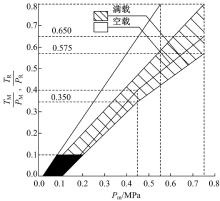
$\begin{matrix} \{\begin{matrix} φ_{1 j} \geq φ_{3 j} \\ φ_{3 j} \geq φ_{2 j} \end{matrix} (16) \end{matrix}$

ECE制动法规对制动力在车轴之间的分配及牵引车与挂车之间的制动协调性都有要求^[14]。满载和空载下, 牵引车轴上的制动器制动力与其静载荷之比T_M/P_m与制动控制阀出口气压P_m的关系不能超过图1中的阴影范围, 标准满载半挂车轴上的制动器制动力与其静载荷之比 $\begin{matrix} T_{R} / P_{R} \end{matrix}$ 与制动控制阀出口气压P_m的关系如图2所示, 而对于其他尺寸和质量参数的半挂车, 采用修正系数 $\begin{matrix} K \end{matrix}$ 对图2所示的法规上、下限进行修正^[15]。制动控制阀出口气压P_m与半挂汽车列车的制动强度有关。

修正系数 $\begin{matrix} K \end{matrix}$ 的计算式为:

$\begin{matrix} \begin{matrix} K = (1.7 - 0.7 \frac{P_{R}}{P_{\max}}) \{1.35 - \frac{0.96}{l_{5}} [1.0 + \\ \frac{(h_{3} - 1.2) P}{P_{R}}]\} - (1.0 - \frac{P_{R}}{P_{Rmax}}) \frac{h_{3} - 1.0}{2.5} (17) \end{matrix} \end{matrix}$

式中:P为半挂车质量, kg; P_Rmax为满载半挂车轴静载荷, N。

	Figure Option View Download New Window
	图1 牵引车制动器制动力要求Fig.1 Requirements of brake force of tractor

	Figure Option View Download New Window
	图2 半挂车制动器制动力要求Fig.2 Requirements of brake force of semitrailer

为了使满载半挂汽车列车满足制动协调性要求, 约束条件可写为:

$\frac{T_{M}}{P_{M}} \leq \{\begin{matrix} 0, 0 \leq P_{m} \leq 0.2 \\ 0.11 (P_{m} - 0.2), 0.2 < P_{m} \leq 7.5 \end{matrix} (18)$

$\frac{T_{M}}{P_{M}} \geq \{\begin{matrix} 0, 0 \leq P_{m} \leq 1 \\ 0.11 (P_{m} - 0.2), 1 < P_{m} \leq 4.5 \\ 0.075 (P_{m} - 4.5) + 0.35, \\ 4.5 < P_{m} \leq 7.5 \end{matrix} (19)$

$\frac{T_{R}}{P_{R}} \leq \{\begin{matrix} 0, 0 \leq P_{m} \leq 0.2 \\ K_{c} \times 0.1 (P_{m} - 0.2), \\ 0.2 < P_{m} \leq 4.5 \\ K_{c} [0.08 \times (P_{m} - 4.5) + 0.41], \\ 4.5 < P_{m} \leq 7.5 \end{matrix} (20)$

$\frac{T_{R}}{P_{R}} \geq \{\begin{matrix} 0, 0 \leq P_{m} \leq 1 \\ K_{c} \times 0.08 (P_{m} - 1), \\ 1 < P_{m} \leq 4.5 \\ K_{c} [0.05(P_{m} - 4.5) + 0.41], \\ 4.5 < P_{m} \leq 7.5 \end{matrix} (21)$

式中:K_c为满载修复系数(P取半挂车满载质量)。

由此, 半挂汽车列车制动器制动力分配系数的选择可归结为求解下列优化模型:

$minF (x) = \sqrt[]{\overset{3}{\sum_{i = 1}} \overset{16}{\sum_{j = 1}} (φ_{ij} - z_{j})^{2}} (22)$

$g_{1} (x) = φ_{3 j} - φ_{1 j} \leq 0 (23)$

$g_{2} (x) = φ_{2 j} - φ_{3 j} \leq 0 (24)$

$\begin{matrix} \begin{matrix} g_{3} (x) = \frac{T_{M}}{P_{M}} - 0.11 (P_{m} - 0.2) \leq 0 (25) \\ 0.2 < P_{m} \leq 7.5 \end{matrix} \end{matrix}$

$\begin{matrix} g_{4} (x) = - \frac{T_{M}}{P_{M}} + 0.11 (P_{m} - 0.2) \leq 0 1 < P_{m} \leq 4.5 (26) \end{matrix}$

$g_{5} (x) = - \frac{T_{M}}{P_{M}} + 0.075 (P_{m} - 4.5) + 0.35 \leq 0, 4.5 < P_{m} \leq 7.5 (27)$

$g_{6} (x) = \frac{T_{R}}{P_{R}} - K_{c} [0.1(P_{m} - 0.2)] \leq 0 0.2 < P_{m} \leq 4.5 (28)$

$g_{7} (x) = \frac{T_{R}}{P_{R}} - K_{c} [0.08(P_{m} - 4.5) + 0.41] \leq 0, 4.5 < P_{m} \leq 7.5 (29)$

$g_{8} (x) = - \frac{T_{R}}{P_{R}} + K_{c} [0.08(P_{m} - 1)] \leq 0, 1 < P_{m} \leq 4.5 (30)$

$g_{9} (x) = - \frac{T_{R}}{P_{R}} + K_{c} [0.05(P_{m} - 4.5) + 0.41] \leq 0, 4.5 < P_{m} \leq 7.5 (31)$

此模型为有约束的线性规划, 采用Matlab-Fmincon求解器进行求解。

2.4 优化结果

半挂汽车列车的结构参数如表1所示, 代入优化模型中求解。优化结果为 $\begin{matrix} β_{1} = 0.279 、 β_{2} = 0.280 、 β_{3} = 0.441, \end{matrix}$ 在此固定制动器制动力分配比作用下, 半挂汽车列车的各轴利用附着系数 $\begin{matrix} φ \end{matrix}$

与制动强度 $\begin{matrix} z \end{matrix}$ 的关系如图3所示。当半挂汽车列车满足该制动力分配系数时, 制动抱死顺序始终为最佳抱死顺序。

	Figure Option View Download New Window
	图3 利用附着系数与制动强度的关系Fig.3 Relationships between adhesion utilization and braking severity

3 液力缓速器换挡控制策略设计及整车仿真模型建立

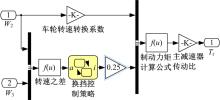
液力缓速器挡位调节模式一般分为手动操纵模式和联动操纵模式。两种模式下液力缓速器的工作挡位分别由驾驶员拨动的挡位键和制动踏板位移决定。两种情况下均受限于驾驶员的判断能力和驾驶水平, 无法根据车辆实际行驶情况做出准确的挡位选择。本文设计的液力缓速器换挡控制策略(见图4)根据牵引车后轴车轮转速与半挂车车轮转速的关系, 调节液力缓速器的挡位, 保证牵引车后轴车轮转速始终大于半挂车车轮转速, 从而实现了半挂车车轮先于牵引车后轴车轮抱死的目标。

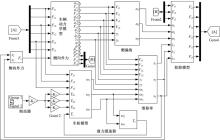
	Figure Option View Download New Window
	图4 液力缓速器控制策略Fig.4 Gear-shifting strategy of hydraulic retarder

根据式(17)和液力缓速器换挡控制策略建立如图5所示的液力缓速器仿真模型。根据式(1)~(16)和图5所示的液力缓速器仿真模型, 建立如图6所示的半挂汽车列车整车制动仿真模型。

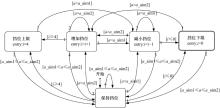
	Figure Option View Download New Window
	图5 液力缓速器仿真子模块模型Fig.5 Simulated model of hydraulic retarder

如图4所示, 采用Matlab/Stateflow设计的换挡控制策略, 这个模块包括5个状态, 分别为保持液力缓速器挡位、减小液力缓速器挡位、增加液力缓速器挡位、液力缓速器挡位上限和液力缓速器挡位下限。仿真开始时, 液力缓速器挡位默认状态为最高挡(四挡), 如果牵引车后轴车轮转速与半挂车轴车轮转速之差 $\begin{matrix} a \end{matrix}$ 小于第1目标速度差a_aim1(-0.1), 转移进入降低液力缓速器挡位的状态; 如果牵引车后轴车轮转速与半挂车轴车轮转速之差大于第2目标速度差a_aim2(0.01), 转移进入增加液力缓速器挡位的状态; 如果牵引车后轴车轮转速与半挂车轴车轮转速之差大于第1目标速度差a_aim1小于第2目标速度差a_aim2, 转移进入保持液力缓速器挡位; 液力缓速器挡位上限和液力缓速器挡位下限两个状态, 保证了液力缓速器挡位 $\begin{matrix} i \end{matrix}$ 的数值始终在0、1、2、3、4之中变化。

	Figure Option View Download New Window
	图6 半挂汽车列车整车仿真模型Fig.6 Brake simulated model of tractor-semitrailer

4 半挂汽车列车直线制动仿真分析

4.1 车轮抱死顺序仿真结果分析

现有研究中, “ I-β ” 分析法只能分析车轮即将抱死情况下的制动稳定性, 而液力缓速器在驱动轴抱死时不产生制动力矩, 所以该分析方法不能体现液力缓速器产生的制动力矩对半挂汽车列车各轮抱死顺序的影响; 附着系数法也是建立在车轮即将抱死的前提下, 同样不适用于分析液力缓速器对半挂汽车列车抱死顺序的影响。本文通过仿真得到的各轴车轮抱死时间点来简单、直观地展现液力缓速器对半挂汽车列车抱死顺序的影响。

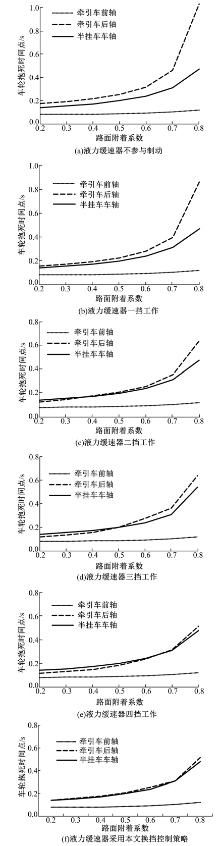
按照GB7258— 2012的要求^[1], 设定该满载半挂汽车列车的制动初速度为60 km/h, 将摩擦制动器制动力矩参数设置成制动强度为0.85对应的数值, 仿真得到不同制动工况下各轮抱死时间点图, 如图7所示。

	Figure Option View Download New Window
	图7 不同制动工况下各轮抱死时间点图Fig.7 Point diagram of wheel lock under different braking conditions

如图7(a)所示, 液力缓速器不参与工作时, 各轴车轮始终遵循最佳抱死顺序, 但是牵引车后轮与半挂车轮抱死时间间隔长, 制动效能低。如图7(b)所示, 液力缓速器一挡工作时, 牵引车后轮与半挂车轮抱死时间间隔有一定程度的减小。

如图7(c)~图7(e)所示, 液力缓速器二挡、三挡和四挡工作时, 虽然牵引车后轮与半挂车轮抱死时间间隔都有进一步的减小, 但是在部分附着系数的路面上, 出现了牵引车前轮、牵引车后轮、半挂车车轮, 这一非最佳抱死顺序。

如图7(f)所示, 对液力缓速器应用换挡控制策略后, 使得牵引车后轮始终在半挂车车轮抱死后抱死, 保证了半挂汽车列车的最佳抱死顺序; 并且, 在低附着系数的路面上, 该换挡控制策略可以最大限度将牵引车前轴车轮的抱死时间点贴近半挂车车轮的抱死时间点。

4.2 制动距离仿真结果分析

如表2所示, 在6种不同工况下半挂汽车列车在不同附着系数路面上的制动距离情况。

表2 液力缓速器6种工况下半挂汽车列车制动距离 Table 2 Braking distance of tractor-semitrailer in six conditions m

$\begin{matrix} μ \end{matrix}$	挡位
$\begin{matrix} μ \end{matrix}$	缓速器不工作	缓速器一挡	缓速器二挡	缓速器三挡	缓速器四挡	加入控制策略
0.2	79.7965	79.7954	79.7946	79.7939	79.7933	79.7950
0.3	59.8818	59.8812	59.8806	59.8702	59.8785	59.8807
0.4	44.9285	44.9217	44.9179	44.9141	44.9093	44.9142
0.5	35.9218	35.9139	35.9112	35.9090	35.9072	35.9129
0.6	29.9278	29.9152	29.8905	29.8847	29.8180	29.8820
0.7	25.5455	25.5351	25.5229	25.5153	25.5143	25.5143
0.8	22.2015	22.1397	22.0912	22.0795	22.0820	22.0820

表2 液力缓速器6种工况下半挂汽车列车制动距离 Table 2 Braking distance of tractor-semitrailer in six conditions m

本文液力缓速器换挡控制策略最大能够缩短制动距离0.1195 m, 但是也使制动距离增加了0.064 m。当液力缓速器不工作和液力缓速器一挡工作时, 半挂汽车列车的制动距离均大于液力缓速器采用该换挡控制策略时的制动距离; 当液力缓速器二挡、三挡工作时, 在路面附着系数μ =0.6、0.7和0.8路面上, 半挂汽车列车的制动距离大于液力缓速器采用该换挡控制策略时的制动距离; 当液力缓速器四挡工作时, 在路面附着系数μ =0.7和0.8路面上, 半挂汽车列车的制动距离等于液力缓速器采用该换挡控制策略时的制动距离。但是在其他情况下, 该换挡控制策略使得半挂汽车列车的制动距离均有不同程度的增加, 制动效能降低, 这是因为在换挡控制策略的操控下, 液力缓速器低挡工作, 制动力矩较小, 半挂汽车列车的制动强度降低, 制动距离相应增加。虽然制动距离增加, 但是半挂汽车列车车轮抱死顺序满足了最佳抱死顺序。

5 半挂汽车列车制动横向稳定性仿真分析

半挂汽车列车在直线制动过程中, 侧向力易使抱死的车轮发生侧向滑动, 对半挂汽车列车的制动稳定性产生不良影响。

为了分析半挂汽车列车在制动过程中遇到短暂侧向力作用时该液力缓速器换挡控制策略是否能提高半挂汽车列车的横向稳定性, 故而在半挂汽车列车仿真模型中加入侧向力模块, 仿真出牵引车横向速度、牵引车横摆角速度、铰接角大小和铰接角速度相关变量的变化情况。

5.1 半挂汽车列车运动方程补充

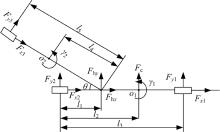
图8为侧向力作用时半挂汽车列车受力分析。图中, F_c为牵引车质心所受侧向力, N; γ ₁为牵引车横摆角速度, rad/s; γ ₂为半挂车横摆角速度, rad/s; $\begin{matrix} θ \end{matrix}$ 为铰接角, (° ); F_h_x为鞍座对牵引车的纵向力, N; F_h_y为鞍座对牵引车的侧偏力, N; F_y₁为牵引车前轮侧偏力, N; F_y₂为牵引车后轮侧偏力, N; F_y₃为半挂车车轮侧偏力, N。表3为补充的半挂汽车列车参数。

	Figure Option View Download New Window
	图8 侧向力作用时半挂汽车列车受力分析Fig.8 Force analysis of tractor semi-trailer combination with lateral force

表3 半挂汽车列车参数补充 Table 3 Supplement of parameters of tractor-semitrailer

如图8所示, 由于半挂汽车列车在侧向力作用下有侧向运动, 需要对上述运动方程进行补充。

牵引车纵向运动方程为:

$\begin{matrix} m_{1} ({\overset{\cdot}{V}}_{x 1} - γ_{1} V_{y 1}) = F_{x 1} + F_{x 2} + F_{hx} (32) \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot}{V}}_{x 1} \end{matrix}$ 为牵引车纵向加速度, m/s²; $\begin{matrix} V_{y 1} \end{matrix}$ 为牵引车侧向车速, m/s。

牵引车侧向运动方程为:

$\begin{matrix} m_{1} ({\overset{\cdot}{V}}_{y 1} + γ_{1} V_{x 1}) = F_{y 1} + F_{y 2} + F_{hy} + F_{c} (33) \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot}{V}}_{y 1} \end{matrix}$ 为牵引车侧向加速度, m/s²。

牵引车横摆运动方程为:

$\begin{matrix} I_{z 1} {\overset{\cdot}{γ}}_{1} = F_{y 1} (l_{3} - l_{2}) - F_{y 2} l_{2} - F_{hy} (l_{2} - l_{1}) (34) \end{matrix}$

半挂车纵向运动方程为:

$\begin{matrix} m_{2} ({\overset{\cdot}{V}}_{x 2} - γ_{2} V_{y 2}) = F_{x 3} - F_{hx} cosθ + F_{hy} sinθ (35) \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot}{V}}_{x 2} \end{matrix}$ 为半挂车纵向加速度, m/s²; $\begin{matrix} V_{y 2} \end{matrix}$ 为半挂车侧向车速, m/s。

半挂车侧向运动方程为:

$\begin{matrix} m_{2} ({\overset{\cdot}{V}}_{y 2} + γ_{2} V_{x 2}) = F_{y 3} - F_{hy} cosθ - F_{hx} sinθ (36) \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot}{V}}_{yz} \end{matrix}$ 为半挂车侧向加速度, m/s²。

半挂车横摆运动方程为:

$\begin{matrix} I_{z 2} {\overset{\cdot}{γ}}_{2} = (- F_{hy} cosθ - F_{hx} sinθ) l_{4} - F_{y 3} (l_{5} - l_{4}) (37) \end{matrix}$

鞍座处的约束方程为^[16]:

$\begin{matrix} \{\begin{matrix} V_{x 2} = V_{x 1} cosθ - [V_{y 1} - (l_{2} - l_{1}) γ_{1}] sinθ \\ V_{y 2} = V_{x 1} sinθ + [V_{y 1} - (l_{2} - l_{1}) γ_{1}] cosθ - l_{4} γ_{2} \\ \overset{\cdot}{θ} = γ_{1} - γ_{2} \end{matrix} (38) \end{matrix}$

牵引车前轴的动态载荷为:

$\begin{matrix} \begin{matrix} F_{z 1} = [F_{hz} l_{1} + m_{1} (- {\overset{\cdot}{V}}_{x 1} + γ_{1} V_{y 1}) h_{1} + \\ m_{1} g l_{2} + F_{hx} h_{2}] / l_{3} (39) \end{matrix} \end{matrix}$

式中: $\begin{matrix} F_{hz} \end{matrix}$ 为鞍座垂直载荷, N。

牵引车后轴的动态载荷为:

$\begin{matrix} \begin{matrix} F_{z 2} = [F_{hz} (l_{3} - l_{1}) + m_{1} ({\overset{\cdot}{V}}_{x 1} - γ_{1} V_{y 1}) h_{1} + \\ m_{1} g (l_{3} - l_{2}) - F_{hx} h_{2}] / l_{3} (40) \end{matrix} \end{matrix}$

半挂车轴的动态载荷为:

$\begin{matrix} \begin{matrix} F_{z 3} = [m_{2} ({\overset{\cdot}{V}}_{x 2} - γ_{2} V_{y 2}) h_{3} + m_{2} g l_{4}] / l_{5} + \\ [(F_{hx} cosθ - F_{hy} sinθ) h_{2}] / l_{5} (41) \end{matrix} \end{matrix}$

鞍座载荷变化为:

$\begin{matrix} \begin{matrix} F_{hz} = [m_{2} (- {\overset{\cdot}{V}}_{x 2} + γ_{2} V_{y 2}) h_{3} + m_{2} g (l_{5} - l_{4})] / l_{5} + \\ [(- F_{hx} cosθ + F_{hy} sinθ) h_{2}] / l_{5} (42) \end{matrix} \end{matrix}$

半挂汽车列车的各轴上车轮侧偏角分别为^[17]:

$α_{1} = \arctan [\frac{V_{y 1} + (l_{3} - l_{2}) γ_{1}}{V_{x 1}}] (43)$

$α_{2} = \arctan (\frac{V_{y 1} - l_{2} γ_{1}}{V_{x 1}}) (44)$

$α_{3} = \arctan [\frac{V_{y 2} - (l_{5} - l_{4}) γ_{2}}{V_{x 2}}] (45)$

式中:α ₁、α ₂分别为牵引车前轴和后轴车轮侧偏角, rad; α ₃为半挂车轴车轮侧偏角, rad。

考虑到半挂汽车列车在制动过程中会出现横向运动, 将轮胎模型换成“ Dugoff” 轮胎模型^[18]描述轮胎纵向力和侧偏力与滑移率和侧偏角间的非线性关系:

$Δ = \frac{μ |F_{zi}| (1 - s_{i})}{2 \sqrt[]{C_{xi}^{2} s_{i}^{2} + C_{yi}^{2} ta n^{2} α_{i}}} (46)$

$f (Δ) = \{\begin{matrix} Δ (2 - Δ), Δ < 1 \\ 1, Δ \geq 1 \end{matrix} (47)$

$\{\begin{matrix} F_{xi} = - \frac{C_{xi} s_{i}}{1 - s_{i}} f (Δ) \\ F_{yi} = - \frac{C_{yi} \tan α_{i}}{1 - s_{i}} f (Δ) \end{matrix} (48)$

式中:i=1, 2, 3; s₁、s₂分别为牵引车前轴和后轴车轮滑移率; s₃为半挂车轴车轮滑移率。

5.2 仿真模型及仿真结果分析

半挂汽车列车侧向力响应模型如图9所示。

	Figure Option View Download New Window
	图9 半挂汽车列车侧向力响应模型Fig.9 Responding model of tractor-semitrailer to lateral force

根据前面的分析, 在μ =0.2的路面上, 液力缓速器四挡工作时, 半挂汽车列车车轮抱死顺序是:牵引车前轴-牵引车后轴-半挂车车轴; 液力缓速器采用本文提出的换挡控制策略后, 半挂汽车列车车轮抱死顺序是:牵引车前轴-半挂车车轴-牵引车后轴。

半挂汽车列车制动初速度, 制动器制动力矩均与第4节中一样, 液力缓速器四挡工作时, 从牵引车后轴车轮抱死的时刻开始, 对牵引车质心施加1000 N的侧向力, 侧向力持续时间0.01 s; 液力缓速器采用本文提出的换挡控制策略时, 从半挂车车轮抱死的时刻开始, 对牵引车质心施加1000 N的侧向力, 侧向力持续时间0.01 s。

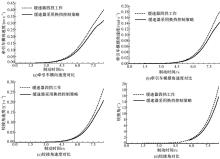
如图10(a)~图10(d)所示, 两种工况下, 半挂汽车列车从开始制动到完全停车为止, 牵引车的横向速度、牵引车横摆角速度、铰接角速度和铰接角大小与制动时间的关系图。与液力缓速器四挡工作的工况相比, 在换挡控制策略的作用下, 4个变量的数值均有不同程度的降低, 牵引车的横向速度减小0.081 m/s, 牵引车横摆角速度减小0.037 rad/s、铰接角减小3.322° , 铰接角速度减小0.057 ° /s。

	Figure Option View Download New Window
	图10 两种工况下牵引车运动参数对比Fig.10 Comparison of motion parameters of tractor under two conditions

6 结论

(1)基于半挂汽车列车车轮最佳抱死顺序, 对液力缓速器挡位进行主动调控, 采用Matlab/Stateflow设计了换挡控制策略, 实现了牵引车后轮转速始终大于半挂车车轮转速的目标。

(2)液力缓速器换挡控制策略基于牵引车后轮与挂车车轮转速的关系, 可以改变原半挂汽车列车在低附着路面上的车轮抱死顺序, 保证了半挂汽车列车的各车轮始终以最佳抱死顺序抱死。

(3)液力缓速器换挡控制策略能够缩短半挂汽车列车在高附着路面上, 液力缓速器低挡工作时的制动距离, 但是在低附着系数路面上, 液力缓速器高挡工作时, 半挂汽车列车的制动距离反而增加。

(4)半挂汽车列车直线制动遇到短暂侧向力时, 该换挡控制策略可在一定程度上减小牵引车和半挂车的侧向速度和横摆角速度, 同时, 牵引车与半挂车的铰接角大小和速度也得到了抑制。

(5)本文换挡控制策略虽然对半挂汽车列车的制动横向稳定性有所改善, 但是效果不显著。为了更好地提升半挂汽车列车制动的横向稳定性, 还需要对半挂汽车列车的气压制动系统进行改进, 根据各轴动态载荷施加制动力矩, 并与液力缓速器挡位进行配合, 保证牵引车和半挂车始终都有相同的制动强度, 减小铰接点的冲撞力, 最好能实现牵引车和半挂车各轴的车轮同时抱死。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	GB7258-2012. 机动车运行安全技术条件[S]. [本文引用:2]
[2]	Wang L, Zheng H. A slip-rate-based braking force distribution algorithm for the electronic braking system of combination vehicle[C]//SAE Technical Paper, 2014-01-2385. [本文引用:1]
[3]	Li B, Rakheja S. Jackknifing prevention of tractor-semitrailer combination using active braking control[C]//SAE Technical Paper, 2015-01-2746. [本文引用:1]
[4]	马建, 陈荫三, 余强, 等. 缓行器对制动稳定性影响评价[J]. 交通运输工程学报, 2002, 2(1): 105-109. Ma Jian, Chen Yin-san, Yu Qiang, et al. Evaluation of retarder to automobile braking stability[J]. Journal of Traffic and Transportation Engineering, 2002, 2(1): 105-109. [本文引用:1]
[5]	赵迎生, 何仁, 王永涛, 等. 利用电涡流缓速器调节车辆制动稳定性[J]. 江苏大学学报, 2007, 28(4): 309-311. Zhao Yin-sheng, He Ren, Wang Yong-tao, et al. Adjusting vehicle's braking stability using eddy retarder[J]. Journal of Jiangsu University, 2007, 28(4): 309-311. [本文引用:1]
[6]	赵国柱, 魏民祥. 缓速器与行车制动系复合制动稳定性的定量评价[J]. 兵工学报, 2009, 30(2): 185-189. Zhao Guo-zhu, Wei Min-xiang. Quantitative evaluation on the braking stability of the composite braking system composed of a retarder and a service-brake system[J]. Acta Armamentarii, 2009, 30(2): 185-189. [本文引用:1]
[7]	何建清, 高树新, 何仁. 牵引车和半挂车联合辅助制动设计[J]. 专用汽车, 2006(2): 35-38. He Jian-qing, Gao Shu-xin, He Ren. A design about united assistant brake of tractor and semitrailers[J]. Special Purpose Vehicle, 2006(2): 35-38. [本文引用:1]
[8]	赵伟强. 商用半挂车制动意图辨识与制动力分配控制策略开发及验证[D]. 长春: 吉林大学汽车工程学院, 2013. Zhao Wei-qiang. Development and test of intention recognition and braking force distribution control strategies for tractor-semitrailer[D]. Changchun: College of Automotive Engineering, Jilin University, 2013. [本文引用:1]
[9]	边明远. 基于双指数模型的纵向附着系数计算模型[J]. 农业机械学报, 2005, 36(5): 5-8. Bian Ming-yuan. Estimation of longitudinal road friction coefficient based on a dual-exponential model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(5): 5-8. [本文引用:1]
[10]	Myung-Won S, Yoon-Ki P, Kyun K, et al. A simulation program for the braking characteristics of tractor-semitrailer vehicle[C]//SAE Technical Paper, 2000-01-3415. [本文引用:1]
[11]	宋建军. 重型载重汽车液力缓速器及其控制系统研究[D]. 长春: 吉林大学机械科学与工程学院, 2013. Song Jian-jun. Research on hydrodynamic retarder and its control system of heavy truck[D]. Changchun: School of Mechanical Science and Engineering, Jilin University, 2013. [本文引用:1]
[12]	潘公宇. 半挂汽车列车制动性能的研究[J]. 江苏理工大学学报, 1997, 18(4): 17-23. Pan Gong-yu. Research on braking performance of tractor-semitrailer[J]. Journal of Jiangsu University of Science and Technology, 1997, 18(4): 17-23. [本文引用:1]
[13]	宗长富, 李伟, 郑宏宇, 等. 汽车列车电控制动系统制动力分配的控制算法[J]. 汽车工程, 2011, 33(10): 885-910. Zong Chang-fu, Li Wei, Zheng Hong-yu, et al. A controlled algorithm of braking force distribution for the electric braking system of combination vehicle[J]. Automotive Engineering, 2011, 33(10): 885-910. [本文引用:1]
[14]	ECE R-13. Uniform provisions concerning the approval of vehicles of categories M, N and O with regard to braking[S]. [本文引用:2]
[15]	童成前. 基于ECE法规的多轴汽车制动性能分析方法研究[D]. 镇江: 江苏大学汽车与交通工程学院, 2010. Tong Cheng-qian. Study on analysis method of braking performance for multi-axle automobile based on ECE regulation[D]. Zhenjiang: School of Automotive and Traffic Engineering, Jiangsu University, 2010. [本文引用:1]
[16]	高红博. 半挂汽车列车转弯制动方向稳定性及控制策略研究[D]. 长春: 吉林大学交通学院, 2014. Gao Hong-bo. Research on directional stability and control strategy of tractor-semitrailer steering and braking[D]. Changchun: College of Transportation, Jilin University, 2014. [本文引用:1]
[17]	彭涛. 半挂汽车列车非线性稳定性控制研究[D]. 长春: 吉林大学交通学院, 2012. Peng Tao. A study on control of nonlinear stability for tractor-semitrailer[D]. Changchun: College of Transportation, Jilin University, 2012. [本文引用:1]
[18]	Dugoff H P, Fancher P S, Segel L. An analysis of tire traction properties and their influence on vehicle dynamic performance[C]//SAE Technical Paper, 700377. [本文引用:1]

0.0

... 0 引言为了提高制动安全性和可靠性,《机动车安全运行技术条件》^[1]中指出,总质量大于等于12 000 kg的货车和专用作业车、危险货物运输车,应装备缓速器或其他辅助制动装置 ...

... 2012的要求^[1],设定该满载半挂汽车列车的制动初速度为60 km/h,将摩擦制动器制动力矩参数设置成制动强度为0 ...

2014

0.0

... 文献^[2]提出了一种基于滑移率的制动力分配算法,根据牵引车前轮滑移率控制牵引车后轮和半挂车车轮滑移率,保证牵引车前轮先抱死,以提高车辆的制动稳定性 ...

2015

0.0

... 文献^[3]根据牵引车的实际横摆角速度与目标值之间的误差,实施主动制动,可预防半挂汽车列车在低附着路面上发生折叠 ...

2002

0.0

. 2002, 2(1):105-109 DOI:doi:10.3321/j.issn:1671-1637.2002.01.023

Evaluation of retarder to automobile braking stability

缓行器对制动稳定性影响评价

Ma Jian , Chen Yin-san , Yu Qiang

马建, 陈荫三, 余强

提出了装用缓行器后汽车前后制动力分配的广义I曲线概念,导出了同步附着系数的计算公式.建立了带缓行器汽车的制动力与广义I曲线匹配的定性评价法和定量评价法,从而能从制动稳定性角度对缓行器制动力匹配的优劣程度给出评价.

... 文献[4]建立了装备有缓速器的单体汽车的制动力与广义I曲线匹配的定性和定量评价法来评价制动稳定性 ...

2007

0.0

. 2007, 28(4):309-311

Adjusting vehicle's braking stability using eddy retarder

利用电涡流缓速器调节车辆制动稳定性

Zhao Yin-sheng , He Ren , Wang Yong-tao

赵迎生, 何仁, 王永涛

... 文献^[5]提出了将电涡流缓速器输出的制动力矩进行调节并加载在单体车后轮的方法,改善了车辆的制动稳定性 ...

2009

0.0

. 2009, 30(2):185-189 DOI:doi:10.3321/j.issn:1000-1093.2009.02.012

Quantitative evaluation on the braking stability of the composite braking system composed of a retarder and a service-brake system

缓速器与行车制动系复合制动稳定性的定量评价

Zhao Guo-zhu , Wei Min-xiang.

赵国柱, 魏民祥

To quantify the effect of retarder on the braking stability of automobiles, an adhesion coeffi?cient model was built for the composite braking system composed of a retarder and a service-brake sys-tem. The stability of the composite braking jointly provided by the retarder and the service-brake sys?tem was evaluated by the model and the standard of ECE Rl3. The. evaluated results show that the composite braking stability decreases gradually with the increase of the braking force from the re?tarder ;To improve composite braking stability, the braking power distribution coefncient of the ser?vice-brake system was adjusted by the position relationship among the braking power distribution line of the service-brake system, the generalized braking force distribution line and the generalized I curve, and the constraints from ECE Rl 3. Simulation results show that the composite braking stability is im?proved significantly.

为定量评价缓速器对汽车制动稳定性的影响，建立了缓速器与行车制动系复合制动的利用附着系数数学模型，利用该模型，以ECE R13法规为标准对缓速器与行车制动系复合制动稳定性进行了评价，分析表明随着缓速器制动力的增大，复合制动+稳定性将逐渐下降；根据汽车行车制动系制动力分配线、广义制动力分配曲线与广义I曲线的位置关系，以ECE R13法规为约束条件对行车制动系制动力分配系数进行了调整。仿真结果表明复合制动稳定性得到了显著提高。

... 文献^[6]提出安装缓速器的单体车辆需要重新调整制动力分配比 ...

2006

0.0

... 文献^[7]提出一种通过控制器使半挂车预先制动,从而实现牵引车和半挂车联合辅助制动的设计方案 ...

2013

0.0

. 2013, :-

Development and test of intention recognition and braking force distribution control strategies for tractor-semitrailer

商用半挂车制动意图辨识与制动力分配控制策略开发及验证[D]

Zhao Wei-qiang.

赵伟强

商用车电控制动系统是一种非常先进的制动系统，通过实现制动线控化，极大弥补了传统气压制动系统的制动延迟，提高了制动系统的响应时间，从而提高了制动安全性及舒适性，为商用车制动性能的提升带了巨大的空间，是未来商用车制动系统研发的方向。本文依托国家863项目“高品质重型商用车集成开发先进技术”（编号：2006AA110104）及国家自然科学基金项目“基于模型预测的重型半挂车动力学稳定性多目标控制研究”（编号：51075176），在调研国内外商用车电控制动系统理论和应用的现有研究成果基础上，以提高制动安全性及舒适性为目标，以商用车电控制动系统为硬件基础，开发兼顾紧急制动及常规制动的驾驶员制动意图辨识的方法，并在此基础上开发制动辅助、多轴制动力分配等控制策略，为我国商用车电控制动系统的自主研发提供理论支持。论文主要进行了以下几个方面的研究工作： (1)通过分析商用半挂车的结构特性，开发了商用半挂车26自由度非线性车辆动力学模型。文中将多轴半挂车简化为三轴形式：转向轴、驱动轴和挂车轴。所建立的模型主要是从车辆各个总成部件出发，对每一个子系统进行建模。子系统模型包括驾驶员模型、转向模型、发动机模型、传动系模型、制动系模型、车轮模型、轮胎模型、悬架模型、非簧载模型、车体动力学模型、路面模型和空气动力学模型。利用制动及操稳的工况进行了仿真，并与TruckSim对应工况的实验数据进行对比验证。为控制策略的离线仿真及硬件在环实验台验证提供了模型基础。 (2)对电控制动系统关键部件进行了性能分析及特性测试，针对各个执行机构的不同特性开发有针对性的闭环控制方法。通过对比例继动阀的结构进行观察、分析及测试，验证了其开环特性；针对其存在较大迟滞特性的特点，开发了PID结合前馈控制的控制方法，补偿其迟滞造成的闭环控制误差。由于桥控调节器及挂车桥控阀的核心构件均是开关阀，所以对其采用PWM的控制方法，为提高气室目标压力的闭环控制精度，采用了小步长增压的阶梯增压法。通过对这些关键部件进行开、闭环测试，掌握了这些阀的控制方法，为商用车电控制动系统控制策略的开发提供了硬件基础。 (3)搭建了电控制动系统硬件在环实验台，并进行EBS系统关键部件特性测试及EBS控制策略的硬件在环试验台验证。实验台由轮速模拟系统、测控系统、电控制动系统、人机交互系统及动力学实时交互系统组成。利用Matlab/xPCTarget技术搭建了电控制动系统快速原型平台，以软硬件结合的方式构建了电控制动系统硬件在环实验台，对比例继动阀、桥控调节器和挂车桥控阀的闭环特性进行了测试，并以此为基础，结合26自由度商用半挂车动力学模型，对驾驶员制动意图辨识方法、多轴车辆制动力分配控制策略及制动辅助控制策略进行了硬件在环实验台验证。 (4)利用神经网络的方法，建立了兼顾紧急制动及常规制动的驾驶员制动意图辨识模型。通过对制动时驾驶员制动特性的分析并结合EBS系统硬件特性，选定踏板开度及其变化率作为辨识驾驶员制动意图的参数，通过踏板开度辨识驾驶员期望制动减速度，踏板开度变化率辨识驾驶员制动的紧急程度。并选择神经网络的方法，结合小型驾驶模拟器，设计实验方案，采集驾驶员的制动操纵行为及车辆制动减速度，最终建立了同时适用于紧急制动及常规制动的驾驶员制动意图辨识模型，并对模型精度进行了离线验证。 (5)开发了制动辅助控制方法。利用硬件在环实验台，采集多个驾驶员的紧急制动行为，并通过后处理方法得到相应的紧急制动阈值。利用所建立的制动意图辨识模型，开发了制动辅助控制策略。当判断驾驶员有紧急制动意图时，制动辅助控制策略将取代驾驶员，向气室释放最大制动压力，确保制动系统对车辆施加最大的制动功率，并利用实验台对所开发的控制策略进行了验证。 (6)根据稳定性控制目标，分析了商用半挂车各轴分别抱死时的车辆状态，并基于滑移率控制方法，建立了多轴车辆制动力分配控制策略。通过分析确定，多轴车辆各轴的抱死顺序不同，对车辆的制动稳定性影响非常大：1）当前轴先抱死时，车辆稳定且可控；2）当挂车轴先抱死时，车辆稳定但不可控；3）当牵引车后轴先抱死时，车辆将既不稳定也不可控，将处于危险状态。利用TruckSim对分析结果进行了仿真验证。仿真结果验证了半挂车制动稳定性分析结果，即牵引车后轴先抱死是商用半挂车制动过程中最危险状况。根据商用半挂车动力学分析的结果，本文采用基于滑移率控制的方法，建立了多轴车辆制动力分配控制策略，根据车辆的实际状态通过相关控制算法确定目标滑移率，利用PID控制将滑移率控制在目标滑移率附近。利用所开发的26自由度车辆动力学模型及商用车电控制动系统硬件在环实验台，进行了控制策略的验证。综上所述，本文取得的创新性成果如下： (1)通过分析、测试商用车电控制动系统核心执行器的结构、功能及动态特性，搭建了商用半挂车硬件在环实验台，解决了商用车试验难度大，非线性强，试验精度不高等问题，并结合建立的26自由度多轴车辆非线性车辆动力学模型，对所开发的控制策略进行了验证。 (2)通过采集经验丰富的商用车驾驶员制动样本，利用神经网络方法，建立了兼顾紧急制动及常规制动的驾驶员制动意图辨识模型。并对模型进行了离线验证。利用建立的制动意图辨识方法，开发了制动辅助控制策略。 (3)针对多轴汽车抱死给制动安全性带来的隐患，通过对商用半挂车制动时车辆稳定性的分析，确定了牵引车及半挂车各轴抱死顺序对车辆的操纵性及稳定性的影响，提出了多轴车辆各轴抱死的最优顺序；并据此建立了基于滑移率的多轴车辆制动力控制策略；并结合所开发的多轴车辆动力学模型及硬件在环实验台对控制策略进行了验证。

... 文献^[8]指出威伯科研发的产品EBS会优先采用缓速器给牵引车后轴提供制动力,减少牵引车后轴摩擦制动器摩擦片的磨损,同时EBS系统会调节制动气室的压力,使车轮滑移率保持最佳 ...

2005

0.0

. 2005, 36(5):5-8 DOI:doi:10.3969/j.issn.1000-1298.2005.05.002

Estimation of longitudinal road friction coefficient based on a dual-exponential model

基于双指数模型的纵向附着系数计算模型

Bian Ming-yuan.

边明远

提出了一种含有3个参数的双指数形式的纵向道路附着系数计算模型.与目前应用的一些经验模型相比,该模型具有结构形式简单、需拟合参数少、计算量小的特点,能够较好地描述纵向附着系数随车轮滑移率及其他因素非线性变化的规律.通过仿真计算与试验结果以及与魔术公式拟合结果的比较,验证了该模型的有效性.

... 2 轮胎模型采用基于双指数模型的纵向附着系数计算模型^[9]: ...

2000

0.0

... 凸轮型鼓式制动器制动力矩可表示为^[10]: ...

2013

0.0

. 2013, :-

Research on hydrodynamic retarder and its control system of heavy truck

重型载重汽车液力缓速器及其控制系统研究[D]

Song Jian-jun.

宋建军

为了保证重型车辆的行车安全，除行车制动器外，车辆还需配备辅助制动器，常用的辅助制动器有液力缓速器和电涡流缓速器两种。与电涡流缓速器相比，液力缓速器的单位质量制动效能高，且无热衰退现象，因此国外的重型、大功率车辆普遍采用液力缓速器作为辅助制动器。而由于价格和相关政策的原因，我国以前对辅助制动器的应用主要倾斜于电涡流缓速器，导致液力缓速器方面的研究明显落后。随着我国载重汽车辅助制动器相关法规标准的颁布，国外著名液力缓速器生产厂家迅速抢占国内重型汽车辅助制动器市场，因此有必要对液力缓速器进行深入、系统的研究，研发拥有我国自主知识产权的液力缓速器产品。本文从液力缓速器的结构、液压控制系统、性能预测方法和下坡缓速性能等方面对液力缓速器进行了系统的研究，主要的研究工作和结论如下： 1.液力缓速器结构设计与分析在充分考虑重型载重汽车动力传动系结构和液力缓速器自身特点的基础上，根据车辆下坡行驶时的受力平衡方程和国内外相关法规标准对液力缓速器下坡缓速效能的规定，确定了液力缓速器的设计要求，即当转子转速为1064r/min时，由其提供的制动转矩必须大于772N.m。详细分析了开式液力缓速器和闭式液力缓速器的优缺点，设计了一种开式液力缓速器，其转子循环圆直径为358mm，定子循环圆直径为360mm。 2.液力缓速器液压控制系统设计与分析详细分析了VOITH、ZF和ALLISON液力缓速器液压控制系统的特点，在此基础上，根据液力缓速器的控制要求，设计了一种与开式液力缓速器相适应的液压控制系统，该系统可以实现液力缓速器的快速充排油控制，并能根据缓速需求连续地调节液力缓速器工作腔的充液率。阐述了液压控制系统各组成阀的工作原理，并对各组成阀的压力流量特性、流量连续性方程和阀芯动力平衡方程进行了详细分析。 3.液力缓速器性能预测给出了液力缓速器的性能预测流程，建立了液力缓速器计算流域模型和网格模型，确定了描述液力缓速器内部气液两相流动的控制方程，指定了计算模型的边界条件和流体属性，在此基础上采用有限体积法对控制方程进行了离散，并采用SIMPLE算法对离散方程组进行了迭代计算。采用欧拉方程对CFD计算获得的速度分布进行了计算，获得了不同转子转速和充液率下的制动转矩，计算结果表明：制动转矩是转子转速的二次函数，是充液率的线性函数。在此基础上，采用最小二乘曲面拟合方法获得了描述制动转矩随转子转速和充液率变化关系的数学表达式。采用面积加权平均算法对CFD计算获得的出油口压力分布进行了计算，获得了不同转子转速和充液率下的出油口压力值，计算结果表明：出油口压力是转子转速的二次函数，是充液率的线性函数。在此基础上，采用最小二乘曲面拟合方法获得了描述出油口压力随转子转速和充液率变化关系的数学表达式。 4.液力缓速器下坡缓速性能计算与分析建立了液力缓速器下坡缓速性能机电液一体化仿真模型，对定坡度坡道和变坡度坡道下的液力缓速器缓速性能进行了仿真计算。详细分析了液力缓速器的缓速工作过程，并对变速箱挡位和设定车速对缓速性能的影响进行了对比分析，结果表明：当变速箱挡位固定时，设定车速越大，车辆达到设定车度恒速行驶所用的时间越短；当设定车速一定时，变速箱挡位越高，车辆达到设定速度恒速行驶所用的时间越长。提出了评价液力缓速器下坡缓速性能的三个指标：最大动态偏差、速度超调量和恒速位移系数，并对本文研究的液力缓速器进行了评价，评价结果表明本文研究的液力缓速器具有良好的下坡缓速性能。

... m,制动转矩 Tzh与转子转速和充液率的关系^[11]为: ...

1997

0.0

. 1997, 18(4):17-23

Research on braking performance of tractor-semitrailer

半挂汽车列车制动性能的研究

Pan Gong-yu.

潘公宇

... 因此当车轮无法同时抱死时,理想的抱死顺序为牵引车前轮、半挂车车轮和牵引车后轮^[13],要使半挂车得到最佳抱死顺序,约束条件可写为^[12]: ...

2011

0.0

. 2011, 33(10):885-910

A controlled algorithm of braking force distribution for the electric braking system of combination vehicle

汽车列车电控制动系统制动力分配的控制算法

Zong Chang-fu , Li Wei , Zheng Hong-yu

宗长富, 李伟, 郑宏宇

摘　要：为汽车列车提出了一种基于滑移率的电控制动系统制动力分配算法,即根据不同情况,使牵引车后轮和半挂车车轮的目标滑移率随牵引车前轮滑移率而变化。运用Matlab/Simulink和Trucksim软件进行列车在高附着和低附着路面上行驶的联合仿真,结果表明该算法能缩短汽车列车的制动距离,提高了制动稳定性。

... 因此当车轮无法同时抱死时,理想的抱死顺序为牵引车前轮、半挂车车轮和牵引车后轮^[13],要使半挂车得到最佳抱死顺序,约束条件可写为^[12]: ...

0.0

... 2 摩擦制动器制动力分配系数优化文献[12]以曲线 φj-z与直线 φ-z在对应制动强度下的两曲线之差的均方根最小为控制目标,最佳抱死顺序为约束条件对半挂汽车列车的制动器制动力固定分配系数进行优化,但是没有考虑联合国欧洲经济委员会汽车法规(ECE法规)^[14]中对牵引车和半挂车制动协调性的要求,下面将把此要求作为优化约束条件之一,对分配系数进行优化 ...

... ECE制动法规对制动力在车轴之间的分配及牵引车与挂车之间的制动协调性都有要求^[14] ...

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1837448

Study on analysis method of braking performance for multi-axle automobile based on ECE regulation

基于ECE法规的多轴汽车制动性能分析方法研究[D]

Tong Cheng-qian.

童成前

汽车的制动性能是汽车安全行驶的重要保障,ECE制动法规对汽车的制动性能有着明确的要求。双轴汽车的制动性能分析方法,已经成熟并被广泛采用；多轴汽车的制动系统结构与双轴汽车比较更为复杂,以致较难分析其制动性能。近年来,有一些相关的研究,但方法大都是基础性的且繁琐,很难在实际中应用。本文提出一套较完整的基于ECE制动法规的多轴汽车制动性能分析方法。研究成果有： (1)指出以往汽车制动性能评价指标的不足,给出了完整的多轴汽车制动性能评价指标体系。 (2)通过分析ECE制动法规对多轴汽车剩余制动和应急制动性能的要求,分别提出了多轴汽车剩余制动和应急制动性能分析方法。 (3)以三轴汽车为例,推导出多轴汽车的驻车极限坡度计算公式,并对其影响因素进行分析；在此基础上,提出了多轴汽车的驻车制动性能分析方法；另外,首次提出了极限坡度利用率的概念,作为对驻车制动性能分析指标的补充。(4)分析了ECE制动法规对多轴汽车制动力分配的要求,指出目前多轴汽车制动力分配方面的分析方法的不足,提出了基于ECE制动法规的“利用附着系数图示法”；提出了一种新的多轴汽车各轴地面法向反力的计算方法。分析了汽车列车的制动不协调的产生原因、带来的危害以及解决措施；在此基础上,提出了汽车列车制动协调性分析方法。 (5)分析了目前几种常用的制动性能试验,整理出ECE制动法规对几种常用试验方法所对应的制动性能的要求,并给出每个试验的条件、试验方法。最后,按照本文提出的多轴汽车制动性能分析方法,对六辆试验样车的制动性能进行分析和评价,以阐述本文的方法的整个分析过程,同时验证了该方法的正确性和实用性。

... 满载和空载下,牵引车轴上的制动器制动力与其静载荷之比T_M/P_m与制动控制阀出口气压P_m的关系不能超过图1中的阴影范围,标准满载半挂车轴上的制动器制动力与其静载荷之比 TR/PR与制动控制阀出口气压P_m的关系如图2所示,而对于其他尺寸和质量参数的半挂车,采用修正系数 K对图2所示的法规上、下限进行修正^[15] ...

2014

0.0

. 2014, :-

Research on directional stability and control strategy of tractor-semitrailer steering and braking

半挂汽车列车转弯制动方向稳定性及控制策略研究[D]

Gao Hong-bo.

高红博

近年来，伴随着甩挂运输的大范围推广，半挂汽车列车已经成为了公路运输车辆的主体，但由于汽车列车自身结构的复杂性、车辆安全性评价体系不完善以及牵引车和半挂车匹配不合理等因素，导致由半挂汽车列车引发的交通事故一直居高不下。车辆制动稳定性直接影响车辆的行驶安全，作为高效运输工具的半挂汽车列车在制动时，由于特殊的车辆结构和行驶环境，比单体车辆更容易发生失稳，尤其是在弯道制动，极易发生甩尾、折叠甚至侧翻等危险工况，从而引发恶性交通事故。因此，开展半挂汽车列车弯道制动的方向稳定性研究，分析车辆转弯制动的失稳机理，提出改善车辆转弯制动方向稳定性的控制策略，对保障公路货物运输的安全、顺畅有重要的现实意义。本文首先建立了包括制动系、转向系、非线性轮胎、悬架和鞍座组成的半挂汽车列车底盘系统模型，其中利用相关数据完成了轮胎模型的特性仿真。在此基础上根据车辆动力学原理，建立了包含载荷转移在内的半挂汽车列车19自由度动力学模型，并利用Matlab/Simulink完成了仿真模型的构建。其次依据半挂汽车列车行驶特点，搭建了由VBOX Ⅲ、陀螺仪、汽车操纵力角测量仪、制动踏板计和制动触发条组成的半挂汽车列车行驶稳定性检测系统。制定了半挂汽车列车稳态圆周运动和定半径转弯制动的试验方案，通过实车道路试验，验证了所建模型的可靠性。利用所建仿真模型，针对半挂汽车列车结构参数和使用参数对车辆转弯制动方向稳定性的影响进行了仿真分析，并提出了改善意见。同时，理论分析了半挂汽车列车转弯制动引起失稳的机理原因，并仿真验证了理论分析的正确性。最后为提高半挂汽车列车转弯制动方向稳定性设计了控制策略，即在控制轮胎最佳滑移率的基础上，以差动制动作为主要执行方式，侧向加速度、牵引车横摆角速度、铰接角和铰接角速度为控制参数的多目标LQR最优控制。控制仿真结果表明，所提出的主动控制策略可显著提高半挂汽车列车弯道制动的横摆稳定性和侧倾稳定性，为车辆稳定性控制系统的进一步研发提供了技术参考。

... 鞍座处的约束方程为^[16]: ...

2012

0.0

. 2012, :-

A study on control of nonlinear stability for tractor-semitrailer

半挂汽车列车非线性稳定性控制研究[D]

Peng Tao.

彭涛

半挂汽车列车作为牵引车与半挂车的重要组合形式，已逐渐成为道路运输车辆的主体。由于普遍采用牵引车和半挂车独立生产和市场经营的运作模式，难以保证牵引车和挂车的匹配和综合安全性，加之国内针对半挂汽车列车安全性评价标准不尽完善、检测技术相对落后等原因，使半挂汽车列车操纵性和行驶稳定性较差，导致交通事故居高不下，甚至有不断加剧的趋势。因此，从牵引车和半挂车匹配和综合安全性的角度，分析和研究汽车列车运动学特性，改善整车操纵和行驶稳定性能，仍然是当前迫切需要解决的问题。围绕半挂汽车列车运动特性分析、行驶稳定域估计以及主动安全控制等方面的问题展开研究，力求从根本上掌握半挂汽车列车稳定性和非线性动力学特性，解决工程中广泛关注的半挂汽车列车操纵稳定性检测、行驶稳定域估计及车辆在侧向风干扰和极限转向情况下的行驶稳定性控制等问题，主要研究内容如下： 1）构建多自由度半挂汽车列车动力学模型，分析车辆在不同载荷和转向条件下的运动响应及失稳的形式和特点；应用GPS技术和惯性测量技术集成，开发适用于半挂汽车列车操纵和行驶稳定性的检测装置，并对实车进行典型工况试验测试；根据所研究对象合理简化半挂汽车列车动力学模型并验证模型可靠性。 2）基于半挂汽车列车动力学系统相关特性，从系统稳态转向平衡点、非稳态转向平衡域及系统能量转化角度对车辆转向稳定性进行分析，掌握半挂汽车列车和牵引车单车在不同行驶条件下各状态参量平衡点、平衡域变化及系统能量转化规律；定性和定量分析半挂车对牵引车及整车协同运动的影响。 3）依据分岔理论、中心流定理和混沌理论，在构建包含Pacejka轮胎魔术公式的半挂汽车列车动力学系统Jacobian矩阵的基础上，分析车辆稳态转向临界状态时的鞍结分岔特性，获得外界干扰条件下系统平衡点及分岔形式的变化规律，并对考虑纵向速度和转角幅值变化的车辆动力学系统在非稳态转向条件下是否存在混沌运动问题进行了初步探讨。 4）依据二自由度单车行驶稳定域的John分析方法，构建包含三次项轮胎公式的车辆系统二次型Lyapunov能量函数，利用Lagrange切点法确定能量函数边界条件并依据Lyapunov稳定性理论求解车辆行驶稳定域；通过分析上述方法的局限，提出改进方法：构建包含Pacejka轮胎魔术公式的车辆系统二次型Lyapunov能量函数，利用系统能量转化特性确定能量函数边界条件并对车辆行驶稳定域进行估计；从定性和定量角度对两种方法估计的车辆行驶稳定域进行对比分析，并通过实车和仿真试验验证改进方法的准确性。 5）提出考虑轮胎参数摄动和侧向风干扰的半挂汽车列车线性分式变换(LFT)模型；基于鲁棒控制理论，应用主动前轮转向和鞍座主动横摆力矩控制策略，利用H回路成形方法和期望状态输出的H范数指标设计多输入多输出的H前馈和反馈综合控制器；通过车辆在侧向风干扰和极限转向输入条件下的半挂汽车列车运动仿真试验，分析和验证控制器对于消除车辆参数摄动和外界不确定因素干扰的影响以及提高车辆直线保持性和期望状态跟踪性方面的控制效果。

... 半挂汽车列车的各轴上车轮侧偏角分别为^[17]: ...

0.0

... 轮胎模型^[18]描述轮胎纵向力和侧偏力与滑移率和侧偏角间的非线性关系: ...