电动汽车(Electric vehicle, EV)以其良好的环境保护和能源调整效应, 成为推动车辆节能减排, 实现汽车产业技术转型、升级以及跨越发展的主流技术方向。而电动汽车所具备的特性则完全符合现代物流业的客观要求, 与近年来所提出的“ 绿色物流” ^[1]发展方向一致。在政策引导和示范运营推广下, 电动汽车已在物流领域进行初步尝试, 在城市区域为货物进行配送。作为电动汽车配送的核心问题, 电动汽车车辆路径问题受到广泛关注。

电动汽车是由全部或部分电能驱动的车辆类型。但目前由于电池技术问题, 受限的续驶里程使得电动汽车在车辆路径问题上与传统汽油车不相同。并且当完成行程所需的里程不能得到满足时, 车辆需要在行驶途中前往充电站补充电量。近几年, 国内外学者对基于电动汽车的车辆路径问题研究不多。大部分是通过考虑不同的影响因素(如续驶里程约束、充电约束、载重约束或者时间窗约束等)去建立模型, 最后采用算法进行求解。Sevgi等^[2]针对电动汽车续驶里程少和充电设施缺乏的问题, 考虑了时间窗的约束, 提出了绿色车辆路径问题, 运用两种启发式算法求解以求到达终点时总的行驶距离最少。Schneider等^[3]研究了电动汽车在物流问题“ 最后一公里” 的应用, 考虑了顾客时间、货物质量、续驶里程的约束, 提出了电动物流车路径优化和调度模型, 避免了配送货物的长时间无用路线, 且能在剩余里程不能满足配送任务的情况下选择合适的充电站充电。Conrad等^[4]考虑了里程的约束并允许车辆在客户点进行充电, 提出充电车辆路径问题, 最后预测了平均行驶里程。Worley等^[5]同时结合充电站选址问题和电动汽车车辆路径问题建立了模型。刘华旭^[6]综合考虑了续驶里程约束、充电需求和充电时间, 建立了电动汽车物流配送调度模型, 并采用蚁群算法进行求解, 最后分析了各配送计划的合理性。高升^[7]构建了以总配送成本最小为目标的电动汽车车辆路径问题模型。

在上述研究中, 所有信息都是确定的。但在实际物流配送中, 一些信息(如顾客需求和交通状况)往往存在不确定性。这些不确定的信息很有可能会动态改变路线, 这时需要及时进行调整。因此, 从20世纪90年代开始, 动态车辆路径问题引起人们的广泛关注和研究。Psaraftis^[8]将动态问题定义为:不是所有信息在制定路线之前都已知, 而是随着初始路线的执行逐步获得; 并且一些有关初始路线的信息会随着时间的变化而变化。根据不同的动态特性, 动态车辆路径问题分为多种^[9], 动态需求车辆路径问题是其中一个重要的分支。熊浩^[10]将动态需求车辆路径问题定义为:在现代信息技术条件下和执行路径过程中, 顾客需求相关信息随时间不断地向决策者揭示, 且需要对车辆路径实施实时优化的问题。

目前, 还鲜有专门针对电动汽车动态需求的车辆路径问题的研究。本文重点研究了电动汽车作为配送过程中装载货物的载体, 如何在动态环境中充分发挥其作用并提高配送效率。通过考虑里程约束和充电需求解决了基于电动汽车的动态需求车辆路径问题。规划了合理的配送方案和充电计划, 在满足顾客需求的基础上, 有效避免了在行驶过程中因电量不足导致电池过放或车辆抛锚等情况的发生。

传统的静态车辆路径问题是根据已知的顾客需求输出一组不会发生任何变化的路线组合。而在动态需求车辆路径问题中, 随着初始路线的执行, 路线需要发生变化以快速地响应动态生成的需求。因此, 动态需求车辆路径问题能够及时考虑动态信息的出现, 并随着动态需求信息的输入, 对路线进行实时优化。优化过程相当于对静态车辆路径问题重新进行求解, 属于NP hard问题。对于大型网络而言, 求解速度较慢, 而且信息变化迅速, 有可能花费较多时间求出的最优方案并不适合当前状况。因此需要确定一个如何在输入实时信息后产生输出路线的策略, 去描述行动与系统状态之间的关系。为保证实时动态性, 需要配备相应的车辆导航系统、信息通信系统和中心优化系统等, 用于实时接收、处理和反馈车辆、顾客及路线信息。

由于电动汽车由电能驱动这一特殊性, 充电是电动汽车在行驶过程中面对的问题之一。当电池电量不足以完成整个行程时, 公共充电站为在行驶途中的车辆提供快速、便利的充电服务。本文采用的充电方式为快充, 其能够在30 min~1 h内将车载电池充满。充电站可能不会位于既定的行驶路线上, 从而车辆会偏移行驶路线, 增加额外成本。所以, 充电时间和充电成本的增加使得路线调整更加复杂, 如何为有充电需求的车辆分配最合理的充电站也是本文研究内容之一。

综上所述, 基于电动汽车的动态需求车辆路径问题可以描述如下:车辆首先按照初始路线给上一工作日的预约顾客送货; 但是由于车辆执行配送任务中动态需求的生成, 使得路线需要在线实时调整; 并且在路线更新时需要为有充电需求的路线分配充电站以完成后续行程。由于该问题考虑充电、充电站、载重和动态需求等多个因素, 所以为了简化问题, 本文作如下假设:

(1)每个顾客的货运量均不超过车辆装载能力, 即来自同一顾客的货物只由一辆车配送。

(2)车辆从车场装载货物为预约顾客送货, 并从动态需求上取货送往车场。因此在配送过程中, 不改变路线上被访问的预约顾客及其顺序。

(3)只考虑单个车场问题。所有车辆从该车场出发, 最后返回车场。

(4)为保证动态需求的服务及时性和车辆的配送效率, 信息中心只接收时间窗内的动态需求。在 T0时刻, 车辆开始出发执行初始路线, 此时信息中心同时开始接受动态需求信息。在 Te时刻, 信息中心关闭接收动态需求信息的窗口。

(5)所有车辆从起点出发时, 电池为满电状态。车辆可以在行驶途中进行多次充电。

(6)充电站位置和数量已知。不考虑充电站内部车辆容纳情况, 即充电站无条件满足车辆的充电需求。

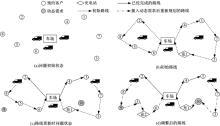
为了更好地描述问题, 本文给出简单示例, 如图1所示。图1(a)中, 车场内有3辆车在等待分派配送任务, 8个预约顾客等待接收货物。图1(b)为求解得到的初始路线:车场→ 2→ 8→ 5→ 6→ 车场(路线1), 车场→ 4→ 1→ 7→ 3→ 充电站1→ 车场(路线2)。当路线更新时(见图1(c)), 车辆1和2分别前往预约顾客8和7。此时需要将生成的2个动态需求(9和10)插入到未完成的路线中。图1(d)为调整后的路线。由于动态需求的生成, 初始路线和初始充电计划都被调整。车辆1需要在离开预约顾客8后前往动态需求9。但是由于车辆偏离行驶路线去访问动态需求9以至于行驶里程增加导致电池电量不足, 因此需要前往充电站充电。而车辆2需要在前往充电站之前绕路去访问动态需求10。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 问题描述示例图Fig.1 Simplified example of problem description

对于动态需求车辆路径问题的求解, 首先需要安排车辆的初始路线。初始路线是根据预约顾客需求提前制定的配送方案。把初始路线求解看作考虑充电、里程约束和载重约束的车辆路径问题, 目标为总成本最小。总成本由派车成本、行驶费用及充电费用组成。利用混合整数规划构建模型。模型参数如下: C0为总成本, 元; tij为从点 i到点 j的行驶时间(min), t_ij= dij40km/h× 60; Cfk为派车成本, 元; Djk为车辆 k到达点 j的剩余里程, km; Ctk为行驶成本, 元; Dmax为车辆最大行驶距离, 150 km; Crk为充电成本, 元; dij为点 i到点 j的行驶距离, km; cf为单位派车成本, 50 元/车辆数; qj为预约顾客 j的货物质量, kg; ct为单位行驶成本, 1 元/min; Wmax为车辆装载容量, 200 kg; cc为单位充电成本, 30元/充电次数; tc为充电时间, 30 min; C为预约顾客集合。 zj为0-1变量, 当点 j有充电站时, 为1; 否则, 为0。 K为车辆集合; O'为终点(车场)。 F为充电站集合; O为起点(车场); yjk为0-1决策变量, 当车辆 k在点 j充电, 为1; 否则, 为0。 xijk为0-1决策变量, 当车辆 k从点 i行驶到点 j, 为1; 否则, 为0。其中常量参数的取值依据常识经验和实例数据来源(见第4节), 确定常量参数取值。不同于路线更新策略的在线求解, 初始路线为离线求解, 因此对实时性要求不高。考虑到网络和约束的复杂性, 本文应用遗传算法对初始路线模型进行求解。

MinC0=∑k∈KCfk+Ctk+Crk1

Where

Cfk=cf(1-x00'k)(2)

tk=ct[∑j∈C⋃F⋃O∑i∈C⋃F⋃Oxijktij](3)

Crk=cc∑j∈Fyjk4

Subject to:

∑i∈C⋃F⋃Oxijk=1, ∀j∈C, ∀k∈K5

∑∀i∈C⋃F⋃Oxijk=∑∀m∈C⋃F⋃O'xjmk6

∀j∈C⋃F, ∀k∈K

xOjk=1, ∀j∈C⋃F⋃O', ∀k∈K7

xiO'k=1, ∀i∈C⋃F⋃O, ∀k∈K8

Djk=[Dik(1-yik)+yikDmax-dij]xijk9

∀j∈C⋃F⋃O', ∀i∈C⋃F⋃O, ∀k∈K

Djk≥0, ∀j∈C⋃F⋃O', ∀k∈K10

Dok=Dmax, ∀k∈K11

∑j∈C∑i∈C⋃F⋃Oxijkqj≤Wmax, ∀k∈K12

yjk≤zj, ∀j∈V, ∀k∈K13

yjk=0, 1, ∀j∈V, ∀k∈K14

xijk=0, 115

∀j∈C⋃F⋃O', ∀i∈C⋃F⋃O, ∀k∈K

式(1)表示总成本; 式(2)表示基于派遣车辆数的派车成本; 式(3)表示行驶成本, 由行驶里程决定; 式(4)表示由充电次数确定的充电成本; 式(5)确保每个预约顾客都被访问到; 式(6)表示流量守恒准则, 即车辆达到某节点后需保证离开该点; 式(7)(8)要求车辆从车场出发, 最后返回车场; 式(9)(10)为里程约束, 即保证车辆抵达任意节点时, 其剩余里程不能小于0, 车辆按照两点直线行驶; 式(11)表示车辆从起点出发时, 电池为满电状态; 式(12)为载重约束, 即确保载货质量不超过车辆装载容量; 式(13)确保车辆只能在充电站充电; 在式(14)(15)中, 决策变量 yjk和 xijk为0-1变量, xijk为初始路线, yjk为初始充电计划。

在执行初始路线的过程中, 为满足不断生成的动态需求, 需要提出一种路线更新策略实时调整路线。目前, 现有的一次性策略^[11]有:先来先服务策略(First come first served, FCFS)、随机队列中心定位策略(Stochastic queue median, SQM)和邻近优先策略(Nearest neighbor, NN)。相关的路线更新启动机制主要有两种:一种是顾客处更新路线, 对于这种更新机制, 如果两个顾客相距较远, 行驶时间较长, 将需要响应更多的动态需求, 并且服务时效性较差; 另外一种是更新时间, 即每隔一段时间更新路线。这种机制可通过设置不同的更新时间调整策略以避免响应过多的动态需求, 实用性比较强。因此, 本文选择更新时间作为路线更新启动机制。并在此基础上, 综合考虑充电站位置、里程约束、载重约束和动态需求, 提出了路线更新策略, 目标为额外成本的最小化。额外成本是由于插入动态需求或者分配充电站所产生的额外费用, 包括因改变充电计划而产生的额外充电费用和因偏离行驶路线而造成的额外行驶费用。成本问题是物流作业中最重要的考虑因素之一。由于本文不涉及时间目标(时间窗、需求相应时间和排队时间等), 因此以额外成本作为策略目标去衡量方案优劣较为合理。路线更新策略流程如下所示。

Step1 启动求解策略, 未执行完的配送路线及待分配的车辆组成可插入路线集合。这时h=0。

Step2 h=h+1。

Step3 插入动态需求。将所有未服务完的动态需求按照到达时间顺序插入到可插入路线集合中, 得到第 h个待选配送路线方案, 里面有 n条配送路线。这时, k=0。

Step4 k=k+1。

Step5 判断第 h个待选配送路线方案中的第 k条配送路线是否满足载重约束, 如不满足, 重新插入动态需求, 返回Step2; 如满足, 转Step6。

Step6 为有充电需求的配送路线分配充电站。根据里程约束判断第 h个待选配送路线方案中的第 k条配送路线是否需要充电。如果不满足里程约束, 则建立充电路线优化问题模型为该配送路线分配充电站, 生成充电计划, 然后转入下一步; 如满足, 直接转入Step7。

Step7 判断对第 h个待选配送路线方案中的所有配送路线都执行了Step5和Step6。如果k=n, 则转入Step8; 如果 k≠n, 返回Step4。

Step8 计算第 h个待选配送路线方案的目标函数(不满足载重约束的待选配送路线方案的目标值为∞ )。

Step9 判断是否已经遍历完所有的待选配送路线方案。如果 h=q(q为待选配送路线方案个数), 则转入Step10; 如果 h≠q,重复Step2~Step8。

Step10 比较各待选配送路线方案的目标函数值, 从中选出最小目标函数值所对应的待选配送路线方案作为最优配送路线。最优配送路线与其对应的充电计划和行车路径作为优化后的配送方案输出。

3.1 插入动态需求

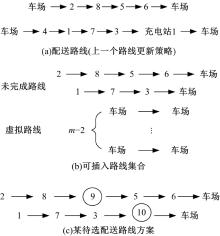
在路线更新策略流程中, 第3步为插入动态需求, 其输出一个待选配送路线方案, 示例如图2所示。图2(a)为上一个路线更新策略输出的配送路线; 图2(b)为路线更新时的系统状态。此时, 2辆车在外执行配送任务, 将要到达的节点分别为预约顾客2和1, 余下行程称为未完成路线。车场内现有 m-2台等待分配任务的车辆, 把它们看作 m-2条中间不访问任何节点的虚拟路线。虚拟路线与未完成路线构成了可插入路线集合。由于动态需求的插入, 导致行驶偏移路线和行驶里程增加, 以至于初始充电计划可能不再适用。因此在未完成路线中插入动态需求时, 不考虑初始充电计划, 即删除初始路线2中被分配的充电站1。插入点为可插入路线集合中任意两个相邻节点之间。插入点的确认解决了动态需求何时被访问的问题。从图2(b)可以看出, 当插入第1个动态需求时, 共有 m+5个插入点(未完成的路线有7个, 虚拟路线有 m-2个)。随着动态需求的不断插入, 节点增多(动态需求也为一个节点)导致插入点也在增加。当插入第 i个动态需求时, 共有 m+i+4个插入点。假设有 p个动态需求, 可得到 ∏i=1pm+i+4个待选配送路线方案。从未遍历的多个待选配送路线方案中选取一个待选配送路线方案。图2(c)为其中的一个(p=2)。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 插入动态需求示例Fig.2 Simplified example of inserting dynamic demands

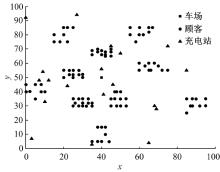
算例的主要数据主要来源于Solomon设计的C101, 其中包括1个车场地理位置、100个顾客地理位置和25辆车。在网格上随机生成20个充电站(编号S1~S20)地理位置。各节点(车场、顾客和充电站)地理位置(x, y)如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 各节点地理位置Fig.3 Node locations

4.1 动态需求生成

从100个顾客中随机选取50个顾客作为动态需求(编号50~100); 剩下顾客作为预约顾客(编号1~50)。应用泊松分布产生动态需求的到达时间。当到达率 λ=5时(参数 λ表示单位时间1 h内生成的平均动态需求个数), 在时间窗内(本文假设信息中心接收动态需求信息的时间窗为8:00~15:00)共生成30个动态需求生成。结合C101数据, 以小时为时间单位对各动态需求位置进行统计, 如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 动态需求的位置分布(8:00~15:00)Fig.4 Location distribution of dynamic demands (8:00~15:00)

4.2 初始路线求解

针对50个预约顾客的初始路线如表1所示。由表1可以看出, 共有8辆车被派出执行预约顾客的配送任务。但由于里程受限, 路线5和7需要在充电站补充电池电量。为了可视化效果更好, 在网格上规划出路线(以路线5为例), 如图5所示。

表1

Table 1

表1(Table 1)

表1 初始路线 Table 1 Initial routes 车辆 初始路线 目标 (总成本/元) 1 车场-24→ 26→ 17→ 18→ 29→ 28→ 27→ 25→ 车场 271.74 2 车场-30→ 33→ 22→ 12→ -车场 157.59 3 车场-42→ 41→ 43→ 44→ 36→ 车场 165.85 4 车场-45→ 50→ 1→ 车场 179.75 5(充电) 车场-21→ 11→ 4→ 3→ S17→ 39→ 40→ 34→ 31→ 23→ 车场 458.96 6 车场→ 32→ 38→ 37→ 35→ 车场 236.51 7(充电) 车场→ 14→ 16→ 6→ 10→ 8→ S1→ 20→ 2→ 7→ 9→ 5→ 车场 388.65 8 车场→ 19→ 15→ 13→ 49→ 48→ 47→ 46→ 车场 230.74

表1 初始路线 Table 1 Initial routes

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 行驶路线(路线5)Fig.5 Driving path (route 5)

4.3 路线更新结果

随着动态需求的加入(表2中带下划线的编号), 根据路线更新策略对路线动态调整, 并对有充电需求的路线分配充电站。首先, 设置更新时间为60 min(即每隔60 min更新路线), 对路线更新过程进行仿真, 结果如表2所示。调整后的路线起点为该车辆将要到达的下一个节点。

表2

Table 2

表2(Table 2)

表2 路线更新结果 Table 2 Result of updating routes 更新 时间点 车辆 调整后的路线 9:00 1 17→ 18→ 29→ 28→ 27→ 25→ 55→ 车场 2 12→ 车场 3 44→ 36→ 车场 4 50→ 1→ 车场 5(充电) 21→ 11→ 4→ 3→ S10→ 39→ 40→ 52-34-31-54-57-51→ 23→ 车场 6 38→ 37→ 53→ 35→ 车场 7(充电) 6→ 10→ 8→ S1→ 20→ 2→ 7→ 9→ 5→ 车场 8(充电) 15→ 13→ S17→ 49→ 48→ 47→ 4→ 6→ 56→ 车场 10:00 1 29→ 28→ 27→ 61→ 25→ 55→ 车场 4 车场 5(充电) 4→ 3→ 58→ S10→ 39→ 40→ 52→ 34→ 63→ 31→ 54→ 57→ 51→ 23→ 车场 6 车场 7(充电) S1→ 20→ 59→ 2→ 7→ 9→ 5→ 车场 8(充电) S17→ 49→ 62→ 48→ 47→ 46→ 56→ 60→ 车场 11:00 1 25→ 55→ 70→ 车场 5(充电) 39→ 65→ S19→ 40→ 68→ 52→ 34→ 63→ 31→ 54→ 66→ 57→ 51→ 23→ 车场 6 车场 7 20→ 69→ 67→ 59→ 2→ 7→ 9→ 5→ 车场 8 48→ 47→ 64→ 46→ 56→ 60→ 车场 12:00 5(充电) 39→ 65→ S19→ 40→ 68→ 52→ 34→ 63→ 31→ 54→ 66→ 72→ 57→ 51→ 23→ 车场 7 2→ 7→ 9→ 71→ 5→ 车场 8 60→ 73→ 车场 13:00 5(充电) S19→ 40→ 68-52→ 34→ 74→ 63→ 31→ 54→ 66→ 72→ 57→ 51→ 23→ 车场 7(充电) 7→ 9→ 71→ 5→ S2→ 75→ 车场 14:00 5(充电) 68→ 76→ 52→ 34→ 74→ 63→ 31→ 54→ 77→ 66→ S7→ 72→ 57→ 51→ 23→ 车场 7(充电) S2→ 78→ 79→ 75→ 车场 15:00 5(充电) 52→ 34→ 74→ 63→ 31→ 54→ 77→ 66→ S7→ 72→ 57→ 51→ 23→ 车场 7 78→ 79→ 80→ 75→ 车场

表2 路线更新结果 Table 2 Result of updating routes

(1)当9:00时, 路线更新策略第一次启动。此时, 初始路线中所派出的8辆车依旧在执行配送任务。8:00~9:00期间产生的6个动态需求(51~56)分别被插入到路线1、5、6和8。对于路线8而言, 由于动态需求56的插入, 导致车辆现有的剩余里程不足以完成整个行程, 因此车辆需要在服务完预约顾客13后前往充电站17补充电量。而对于路线5来说, 随着多个动态需求的插入, 初始充电计划已经不再适合, 因此重新分配了充电站, 从充电站17变成充电站10。由于没有被插入任何动态需求, 路线2、3、4和7未有任何变化。

(2)当10:00时, 车辆2和3已经返回车场并等待分配新的配送任务。而车辆4和6已经完成所有配送任务, 正在返回车场的路上。9:00~10:00期间共产生6个动态需求(57~62), 分别被插入路线1、5、7和8中。虽然这些路线有了稍许变化, 但是依然满足里程约束, 因此并不没有改变上一阶段的充电计划。

(3)随着时间的推移, 路线及充电计划在不断地动态调整。部分车辆由于已经完成已有的配送任务且又不需要去访问动态需求而返回车场, 重新等待新的配送任务分配。当动态需求接收时间窗关闭时(15:00), 只剩下两条路线在线。但根据里程约束, 路线5需要分配充电站。而在路线7中, 车辆只要服务完4个动态需求返回车场即可。

(4)即使在路线更新策略中允许重新派出车辆, 但所有的动态需求依然插入到未完成的路线上。这是因为在当前数量的动态需求下, 一次充电就可以满足插入路线的充电需求, 而且重新派车成本(50元)略高于一次充电成本(30元), 所以每当路线更新时在满足载重约束的前提下策略优先选择插入路线一次充电。

4.4 参数分析

在路线更新策略中, 更新时间的设置对路线调整的结果影响很大。因此为了分析更新时间对路线调整结果的影响, 针对不同的参数值设置进行试验, 并以总额外成本和运行时间为指标评价路线更新策略的优越性。将总额外成本定义为满足时间窗内生成的所有动态需求所产生的额外费用。将运行时间定义为运行一次策略所花费的平均计算时间。平均计算时间由时间窗内多次运行策略的总时间除以运行策略次数求得。

参数分析结果如表3所示, 从表中可以得到如下结论:

(1)当更新时间最长时(80 min), 运行时间为185.873 s(3 min5 s), 为8个试验中最长。这是因为更新时间间隔较长导致每个时间段所积累的动态需求较多, 所以遍历完所有的待选配送路线方案所耗费的时间较长。再加上有充电需求的插入路线增加, 使得充电模型求解时间也在增长。但相比较于配送时间、行驶时间及充电时间来说, 该运行时间较少, 是在可接收范围之内。结果说明本文所提出的路线更新策略具有较好的在线实时处理能力。

表3

Table 3

表3(Table 3)

表3 参数分析结果 Table 3 Parameter analysis 更新时间/min 总额外成本/元 运行时间/s 10 390.28 0.0062 20 390.38 0.0093 30 418.91 0.0104 40 412.38 0.0137 50 563.64 131.2694 60 445.36 0.0139 70 585.28 150.6474 80 538.47 185.8730

表3 参数分析结果 Table 3 Parameter analysis

(2)由于动态需求和充电次数增多, 所以整体上(更新时间为50 min除外)总额外成本和运行时间随着更新时间的增加呈上升趋势。即使有个别相邻值下降, 但相差不大。更新时间为50 min的试验有个较大的突变是因为在路线更新前期节点之间距离较远, 所以时间段内已经访问的节点数较少, 未完成的路线中的节点较多。这将导致遍历完所有的待选配送路线方案所花费的时间和充电模型求解时间变长; 更新时间为60 min的路线更新中, 时间段内已经访问的节点数变多, 而在需处理的动态需求数与50 min的试验相差不大, 所以相比较于更新时间为50 min, 更新时间为60 min的总额外成本和运行时间明显减少。

(3)无论从总额外成本还是运行时间来看, 更新时间为10 min的路线更新策略性能最优。更新时间少的路线更新策略不仅能快速满足动态需求, 还能降低成本。但当解决具有大量动态需求的车辆路线问题时, 实时性越强的路线更新策略对软硬件要求越高, 信息中心可综合考虑自身的条件及动态需求数量, 动态地调整路径更新策略。

首先, 在考虑预约顾客需求、充电、里程约束和载重约束的基础上, 建立了基本车辆路径问题, 利用遗传算法求解模型得到初始路线。然后, 提出一种基于更新时间的路线更新策略对路线进行在线实时调整以满足不断生成的动态需求, 并且建立充电模型对有充电需求的路线分配充电站以避免因电量不足造成电池过放或车辆抛锚等情况。最后, 由50个预约顾客、50个动态需求和20个充电站组成的算例仿真了路线更新过程。随着动态需求的插入, 路线和充电计划不断发生变化, 但由于重新派车成本较高, 对于插入路线而言, 路线更新策略会优先选择一次充电方案。由参数分析试验结果可得:本文路线更新策略具有较好的实时性和实用性。