基于动态反应时间的全速度差模型

引用本文

宋现敏, 邓晓磊, 高铭, 曲昭伟. 基于动态反应时间的全速度差模型[J].吉林大学学报（工学版）, 2017,47(6): 1703-1709
SONG Xian-min, DENG Xiao-lei, GAO Ming, QU Zhao-wei. Full velocity difference model based on dynamic reaction time[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1703-1709 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706005
Permissions

基于动态反应时间的全速度差模型

宋现敏, 邓晓磊, 高铭, 曲昭伟

吉林大学交通学院,长春 130022

通讯作者：曲昭伟(1962-),男,教授,博士生导师.研究方向:交通控制,交通视频检测.E-mail:quzw@jlu.edu.cn

作者简介:宋现敏(1978-),女,副教授,博士.研究方向:交通控制.E-mail:songxm@jlu.edu.cn

基金:国家自然科学基金项目(51278520,51278220)

摘要

为了描述真实路网交通流的跟驰行为,将车辆状态分为强跟驰、弱跟驰和自由行驶3种状态,考虑驾驶员对于不同间距的反应时间的差异性,提出了间距与速度差敏感系数函数,构建了基于动态反应时间的全速度差模型,并通过线性稳定性分析得到模型的临界条件。利用Matlab进行数值仿真,分别验证了模型在车辆启动加速、车辆避险减速和交通流从自由流状态向拥堵状态演变3种环境下的准确性,并与最优速度模型(OVM)和全速度差模型(FVDM)进行对比分析。结果表明:本文模型的启动延迟时间为1.5 s,拥堵传播速度为17.76 km/h,减速性能比FVDM模型提升了25%,本文模型能更有效地接近交通流的稳定状态。

关键词: 交通运输系统工程; 反应时间; 跟驰模型; 交通仿真

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2017)06-1703-07

Full velocity difference model based on dynamic reaction time

SONG Xian-min, DENG Xiao-lei, GAO Ming, QU Zhao-wei

College of Transportation, Jilin University, Changchun 130022, China

Abstract

In order to describe car following behavior in real road traffic, the car following status is divided into strong car-following, weak car-following and free travel sub-status. Considering the difference of driver reaction time in different space headways, a space sensitivity and velocity difference functions, and a full velocity difference model based dynamic reaction time (DRVM) is established. The stability condition of this model is obtained by using linear stability theory. Three experiences, vehicle acceleration, vehicle emergency deceleration and change of traffic state from free flow to congestion, are simulated in MATLAB. Compared with Optimal Velocity Model (OVM) and Full Velocity Difference Model (FVDM), simulation results show that the starting lag time of DRVM is 1.5 s, the speed of congestion spreading is 17.76 km/h, and the deceleration performance is improved by 25% compared with that of FVDM. The DRVM can be accord with the actual situation and close to stable traffic flow.

Keyword: engineering of communication and transportation; reaction time; car-following model; traffic simulation

Show Figures

0 引言

优化速度模型(Optimal velocity model, OVM)认为后车在跟驰过程中根据交通状况调整自身加速度来接近期望最优速度, 其在交通仿真、智能车辆、交通安全领域具有广泛应用。Bando等^[1]在1995年首次提出OVM, 该模型能够很好地表现交通流的相变、交通失稳特性。在此基础上, 国内外学者对优化速度模型进行了大量探索。Helbing等^[2]利用实际数据对OVM模型进行标定, 并考虑负速度差的影响, 对OVM模型进行扩展, 提出了广义力模型。Jiang等^[3]考虑了前、后两车的正负速度差, 建立了全速度差模型(Full velocity difference model, FVDM), 使模型更具现实性。Tang等^[4]考虑了双车道情况下换道车辆对跟驰行为的影响并建立了基于换道概率的跟驰模型, 得出考虑前车换道概率能够增强车流运行稳定性。Liu等^[5]建立了考虑后车期望速度和安全间距的跟驰模型, 该模型能够克服FVDM模型中会出现负速度的缺点。Yu等^[6]将前车加速度引入到FVDM模型中, 避免了FVDM模型中后车出现加速度过高的现象。金盛等^[7]在FVDM模型基础上考虑前方交通状态, 更加实际地描述了前方多辆车对驾驶行为的影响。徐程等^[8]建立了考虑车辆驾驶过程侧向偏移的跟驰模型, 得出侧向偏移会降低交通流稳定性。Lu等^[9]建立了基于现实水平的三维交通流仿真模型, 在模型中引入避免碰撞的全速度差模型, 并利用实际数据对仿真模型进行验证, 取得较好的效果。Zhou等^[10]考虑了车辆跟驰行为中驾驶员对于自身速度估计过高或过低的现象, 建立了基于速度分布的优化速度模型, 并得出驾驶员对于自身速度估计偏大时更有利于交通流稳定。以上文献均认为驾驶员对不同交通状态的反应时间是相同的, 但实际情况并非如此。Zheng等^[11]研究了换道行为对换道车驾驶员特性的影响, 得出驾驶员在换道前后驾驶特性会发生变化。Ota^[12]的驾驶试验证明不同驾驶员在相同条件下也会选择不同的车头时距。王福建等^[13]的研究表明:驾驶员跟驰过程中存在强跟驰和弱跟驰状态, 强跟驰时, 前、后车间距较小, 后车根据前车状态迅速调整自身速度; 弱跟驰时, 前、后车距离较大, 前车微小速度变化不会影响后车驾驶行为。

在实际跟驰行为中, 前车驾驶员会根据自身期望速度和道路交通状况调整车速, 后车驾驶员根据前车状态做出反馈, 因而前、后车的车头间距和速度差是不断变化的, 驾驶员反应时间也是动态变化的。本文考虑了驾驶员反应时间的动态性, 基于强跟驰和弱跟驰临界车头时距提出了驾驶员动态敏感系数函数, 在FVDM模型基础上建立基于动态反应时间的全速度差模型(Dynamic reaction time velocity model, DRVM), 分析了模型的线性稳定性, 并通过数值仿真验证了车辆加速、减速和交通流状态演变3个情境下模型的有效性。

1 模型建立

1.1 全速度差模型

Jiang等^[3]考虑了前、后两车的正负速度差, 建立了全速度差模型(FVDM), 克服了OVM模型中出现不切实际加速度的情况, 其模型结构如下:

$\begin{matrix} d v_{n} / (dt) = κ [V (s) - v_{n} (t)] + λΔv (1) \end{matrix}$

式中: $\begin{matrix} s \end{matrix}$ 为前、后两车车头间距, m; $\begin{matrix} v_{n} (t) \end{matrix}$ 为第 $\begin{matrix} n \end{matrix}$ 辆车的速度, m/s; $\begin{matrix} Δv \end{matrix}$ 为前、后两车速度差, m/s; $\begin{matrix} V (s) \end{matrix}$ 为最优速度函数; $\begin{matrix} κ 、 λ \end{matrix}$ 分别表示前、后车间距和前、后车速度差发生变化时后车驾驶员反应时间的倒数, 均为定值。。

1.2 DRVM模型

HCM2000定义双车道公路车头时距大于5 s时车辆为自由行驶状态, 前车状态不会对后车产生影响^[14]。本文以车头间距代替车头时距作为判断是否发生跟驰行为的依据, 并将100 m作为判断跟驰行为的阈值。实际行驶过程中存在强跟驰、弱跟驰和自由行驶3种状态, 3种状态下反应时间不同。

后车驾驶员对前车的反应时间越小, 其敏感系数越大; 反之, 敏感系数越小。双曲正切函数能够很好地表达驾驶员反应时间与车间距的关系, 因此本文应用双曲正切函数构建了间距敏感系数函数, 形式为:

$\begin{matrix} V (κ) = κ_{1} + κ_{2} \tan h [t_{1} / (s - l_{c})] (2) \end{matrix}$

式中: $\begin{matrix} l_{c} \end{matrix}$ 为车身长度。

根据文献^[14], 车辆弱跟驰时, 车头间距较大, 反应时间长, 取 $\begin{matrix} κ_{1} = 0.41 \end{matrix}$ 作为基础反应系数, 表示实际弱跟驰敏感系数。当车头间距逐渐减小, 车辆由弱跟驰状态向强跟驰状态过渡, 驾驶员注意力更加集中, 车头时距减小, 取 $\begin{matrix} κ_{2} = 0.22 \end{matrix}$ 作为叠加反应系数, $\begin{matrix} κ_{1} + κ_{2} \end{matrix}$ 为实际强跟驰敏感系数。

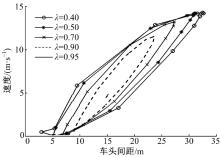
驾驶员在跟驰过程中, 车头间距不同时, 后车对于前车在相同速度差时的反应时间不同。实际经验表明, 驾驶员的反应时间对间距变化比对速度变化更为敏感, 其整体趋势与车头间距变化时相同。在式(2)基础上乘以调整系数 $\begin{matrix} λ \end{matrix}$ , 则速度差敏感系数表达式为:

$\begin{matrix} V (λ) = λV (κ) (3) \end{matrix}$

本文通过仿真试验标定 $\begin{matrix} λ \end{matrix}$ 的取值范围。试验条件如下:在长度l=3000 m的道路上均匀分布 $\begin{matrix} n = 150 \end{matrix}$ 辆车, 初始车头间距为20 m, 车长为5 m, 初始车速为 $\begin{matrix} V (l / n), \end{matrix}$ 在 $\begin{matrix} l \end{matrix}$ 距离内, 始终具有固定数量的车辆。分别仿真不同 $\begin{matrix} λ \end{matrix}$ 取值下速度、车头时距的关系, 如图1所示。

	Figure Option View Download New Window
	图1 不同λ 取值下的车头间距-速度关系Fig.1 Headway-speed at different values of λ

从图1中可以看出:当 $\begin{matrix} λ < 0.5 \end{matrix}$ 时, 车头间距小于极限值5 m, 在实际情况中不可能发生。当 $\begin{matrix} λ = 0.5 \end{matrix}$ 时, 车头间距最小值为5 m, 对应速度值为0, 反映实际情况中前后车恰好刚刚接触的临界情况。而 $\begin{matrix} λ > 0.5 \end{matrix}$ 时, 随着 $\begin{matrix} λ \end{matrix}$ 逐渐增大, 车头间距和速度变化区间都在缩小。当 $\begin{matrix} λ = 0.95 \end{matrix}$ 时变为一个点, 说明交通流在此过程中始终处于初始稳定状态。 $\begin{matrix} λ \end{matrix}$ 取值应该能够体现实际交通中速度和车头间距在大范围内波动的特性, 故本文中将前后车接触的临界条件作 $\begin{matrix} λ \end{matrix}$ 的取值, 即 $\begin{matrix} λ = 0.5 。 \end{matrix}$

将式(2)(3)代入式(1), 得到基于动态反应时间的全速度差模型:

$\begin{matrix} \begin{matrix} \frac{d v_{n}}{dt} = {κ_{1} + κ_{2} \tan h [t_{1} / (s - l_{c})]} [V (s) - \\ v_{n} (t)] + 0.5 {κ_{1} + κ_{2} \tan h [t_{1} / (s - l_{c})]} Δv (4) \end{matrix} \end{matrix}$

2 线性稳定性分析

如果在扰动作用下系统偏离了原来的平衡状态, 当扰动消失后, 系统能够以足够的准确度恢复到原来的平衡状态, 则系统是稳定的; 否则, 系统是不稳定的。为了检验模型(4)在交通流中的稳定性, 假设初始时刻为稳定态, 所有车辆间隔距离都为 $\begin{matrix} h, \end{matrix}$ 对应稳态优化速度为 $\begin{matrix} V (h), \end{matrix}$ 则在整个车队中第 $\begin{matrix} n \end{matrix}$ 辆车的位置可以表示为:

$\begin{matrix} x_{n}^{0} (t) = h n + V (h) t (5) \end{matrix}$

此时, 所有车辆都按照优化速度 $\begin{matrix} V (h) \end{matrix}$ 匀速行驶, 定义 $\begin{matrix} y_{n} (t) \end{matrix}$ 为对第 $\begin{matrix} n \end{matrix}$ 辆车引入的微小扰动, 则第 $\begin{matrix} n \end{matrix}$ 辆车的实际位置可以表示为:

$\begin{matrix} x_{n} (t) = x_{n}^{0} (t) + y_{n} (t) (6) \end{matrix}$

将式(6)代入(4)中并进行线性化, 为表示方便, 记 $\begin{matrix} V (s) = V_{1}, V (κ) = V_{2}, \end{matrix}$ 可得:

$\begin{matrix} \begin{matrix} \frac{d^{2} y_{n} (t)}{d t^{2}} = V'_{2} (h) Δ y_{n} (t) \cdot \\ [V'_{1} (h) Δ y_{n} (t) - \frac{d y_{n} (t)}{dt} + 0.5 \frac{dΔ y_{n} (t)}{dt}] (7) \end{matrix} \end{matrix}$

式中:

$\begin{matrix} \begin{matrix} V'_{1} (h) = {\frac{dV (Δ x_{n})}{dΔ x_{n}}|}_{Δ x_{n} = h} \\ V'_{2} (h) = {\frac{dV (Δ x_{n})}{dΔ x_{n}}|}_{Δ x_{n} = h} \end{matrix} \end{matrix}$

将式(7)中的微小扰动以傅里叶级数形式展开为 $\begin{matrix} y_{n} (t) = Aexp (ikn + zt) \end{matrix}$ 形式, 可得:

$\begin{matrix} \begin{matrix} z^{2} = V'_{2} (h) (e^{ik} - 1) \cdot \\ [V'_{1} (h) (e^{ik} - 1) - z + 0.5 z (e^{ik} - 1)] (8) \end{matrix} \end{matrix}$

令 $\begin{matrix} z = vi, \end{matrix}$ 其中 $\begin{matrix} v \end{matrix}$ 为实数。将其代入式(8)中, 且根据欧拉公式 $\begin{matrix} e^{ik} = cosk + isin k, \end{matrix}$ 进行化简, 令实部和虚部分别为0, 可得到实部和虚部系数表达式分别为:

$\begin{matrix} \begin{matrix} 2 V'_{1} (h) V'_{2} (h) cosk - v^{2} - 2 vV'_{2} (h) sink - \\ 2 V'_{1} (h) V'_{2} (h) co s^{2} k + vV'_{2} (h) cosksink = 0 (9) \end{matrix} \end{matrix}$

$V'_{2} (h) (1 - cosk) (vcosk - v + 2 V'_{1} (h) sink) = 0 (10)$

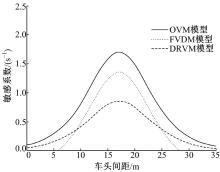
求解式(9)(10)组成的方程组, 并在 $\begin{matrix} k \to 0 \end{matrix}$ 处利用两次洛必达法则, 可得到模型的稳定性条件为:

$\begin{matrix} V'_{1} (h) > V'_{2} (h) (11) \end{matrix}$

图2为本文模型的稳定性临界曲线, 为方便对比, 将OVM和FVDM模型的临界曲线也绘制于图中。从图2中可以看出, 本文模型的稳定性曲线所处位置最低, 因而与FVDM和OVM模型相比, DRVM模型稳定区间更大。

	Figure Option View Download New Window
	图2 临界稳定曲线Fig.2 Neutral stability lines in headway-sensitivity space

3 数值仿真及分析

为了验证模型的准确性, 利用Matlab软件编程分别对OVM、FVDM、DRVM模型实现了车辆启动、车辆减速和环路的仿真, 对比分析了3类模型的有效性。其中仿真时间步长为0.1 s, 采用Helbing标定最优速度函数, 具体形式为:

$\begin{matrix} V (s) = V_{3} + V_{4} \tan h [C_{1} (s - l_{c}) - C_{2}] (12) \end{matrix}$

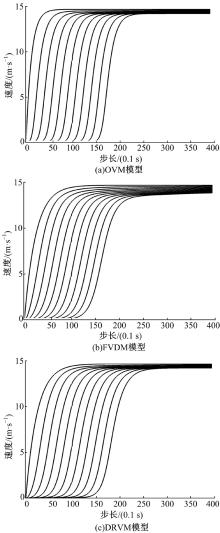
式中:车辆长l_c=5 m; V₃=6.75 m/s; V₄=7.91 m/s; $\begin{matrix} C_{1} \end{matrix}$ 为阻塞密度, C₁=0.13 m^-1; $\begin{matrix} C_{2} \end{matrix}$ 为调整系数, $\begin{matrix} C_{2} = 1.57 。 \end{matrix}$

3.1 车辆启动仿真

信号交叉口红灯启亮时, 车辆将在停车线前排队等待, 下一周期绿灯启亮时, 排队车辆将依次离开停车线。排队的第一辆车前方无车, 可以认为与前车速度差为正无穷。仿真环境中模拟了11辆车, 车辆均匀分布, 车头间距为7.4 m。在 $\begin{matrix} t = 0 \end{matrix}$ 时刻, 信号灯由红灯转为绿灯, 车辆依次启动。分别仿真OVM、FVDM、DRVM模型每辆车启动后的时间步长-速度关系, 结果如图3所示。

	Figure Option View Download New Window
	图3 时间步长-速度关系Fig.3 Relationship of time-step and speed

从以上仿真中可以得到启动过程中的延迟时间。延迟时间是指前、后两车达到相同速度时后车相对前车增加的时间, 用 $\begin{matrix} δ_{t} \end{matrix}$ 表示。从仿真结果可知:第1~4辆车延迟时间波动较大, 而第7~10车延迟时间波动较小, 故利用第7~10辆车延迟时间的均值作为实际延迟时间。利用 $\begin{matrix} δ_{t} \end{matrix}$ 可以计算在拥堵情况下交通波的传播速度 $\begin{matrix} c_{j}, \end{matrix}$ 计算公式为:

$\begin{matrix} c_{j} = h_{w} / δ_{t} (13) \end{matrix}$

式中:h_w为车头间距, h_w=7.4 m。

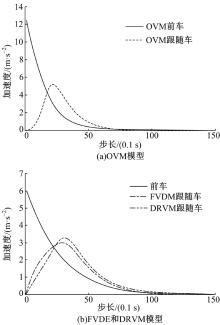
根据仿真结果计算得到以上3个模型的延迟时间和传播速度, 如表1所示。文献[15]指出 $\begin{matrix} c_{j} \end{matrix}$ 的取值范围为17~23 km/h, 由此可知FVDM和DRVM模型都能比较好地体现车辆延迟和拥堵传播过程, 而OVM模型结果偏小。

为了更好地研究启动过程中每辆车的加速度变化, 绘制了OVM、FVDM、DRVM三个模型中第1辆车和第2辆车的加速度-时间关系图, 如图4所示。3个模型中初始车辆加速度都是不断下降的, 第2辆车的加速度先增大后减小。仿真结果表明:OVM模型中第2辆车的加速度约为5 m/s², 此值过大, 其原因为在OVM模型中首车初始加速度大于12 m/s², 这与实际不符。而DRVM和FVDM模型中首车在整个过程中加速度相同, 初始值为6 m/s², 平稳下降, 符合驾驶员对信号相位转变迅速反应的情况。FVDM模型中跟随车的最大加速度为3 m/s², 而DRVM模型跟随车的最大加速度略大于3 m/s², 两者都是比较符合实际的, 但DRVM模型中跟随车加速度未达到最大值之前变化率较小, 相对而言其安全性更好。

表1 车辆延迟时间和拥堵传播速度 Table 1 Delay times of car motions and disturbance propagation speed at jam density

模型	$\begin{matrix} δ_{t} \end{matrix}$ /s	c_j/(km· h^-1)
OVM	1.6	16.65
FVDM	1.4	19.03
DRVM	1.5	17.76

表1 车辆延迟时间和拥堵传播速度 Table 1 Delay times of car motions and disturbance propagation speed at jam density

	Figure Option View Download New Window
	图4 前车和跟随车的加速度Fig.4 Acceleration of leading car and its following

3.2 车辆减速仿真

车辆在行驶过程中加速和减速行为是不断交替的, 相比加速过程, 模型的减速能力直接反映模型的安全性。为测试OVM、FVDM和DRVM模型的减速性能, 对实际环境中的交通事故避险行为进行仿真试验。

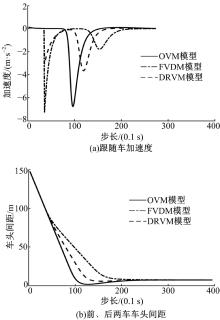
模拟环境:在单行车道上行驶的前车因自身发生事故而停车, 后车在其后150 m处发现前车, 并采取刹车行为措施, 则试验中初始车头间距为150 m, 后车速度为14.5 m/s。通过仿真获得后车在整个过程中的车头间距、加速度的变化特性, 如图5所示。从图5中可以看出:OVM、FVDM和DRVM模型中的最大减速度分别为-6.51、-7.30、-3.17 m/s², 而通常加速度为-4~4 m/s²。由此可知OVM、FVDM模型的减速度过大, 会让驾驶员产生不舒适感, 而本文建立的DVRM模型更加平滑。同时, OVM模型大约在仿真100步长时, 出现车头间距小于5 m的情况, 此时发生了碰撞。FVDM和DRVM模型则不会出现这种情况, 并且DRVM大约在仿真步长为150时达到最小车头间距而停止, 而FVDM则需要大约200时间步长, 说明DRVM能够更好地描述刹车情况下的驾驶行为, 减速性能比FVDM模型提升了25%。

	Figure Option View Download New Window
	图5 OVM, FVDM, DRVM模型的减速度仿真Fig.5 Deceleration simulations of OVM, FVDM and DRVM

3.3 环路仿真

Kerner等^[16]的研究认为在实际交通中存在自由流、同步流和宽运动阻塞3种状态, 而后两者也属于拥堵状态。为研究从自由流状态到拥堵状态的转变过程, 利用本文建立的DRVM模型, 并与OVM、FVDM模型对比, 进行交通相变模拟。设计了单车道封闭环道为模拟试验场地, 其周长L=1500 m, 车辆总数 $\begin{matrix} N = 100 \end{matrix}$ 辆, 初始状态时车辆均匀分布, 并以模型初始车头间距的最优速度为初速度, 则车辆初始位置和速度可表示为:

$\begin{matrix} \{\begin{matrix} x_{1} (0) = 1 m \\ x_{n} (0) = (n - 1) L / N, n \neq 1 \\ v_{n} (0) = V (L / N) \end{matrix} (14) \end{matrix}$

因仿真步长较短, 故车辆在每个时间步长内可看作匀速直线运动。根据运动学公式, 车辆速度和位移更新规则如下:

$v_{n} (t + Δt) = v_{n} (t) + a_{n} (t) Δt (15)$

$\begin{matrix} \begin{matrix} x_{n} (t + Δt) = x_{n} (t) + Δt \frac{v_{n} (t) + v_{n} (t + Δt)}{2} \end{matrix} \end{matrix}$ (16)

按照以上参数设置进行仿真, 记录车辆每一时间步长的速度、加速度和车头间距。

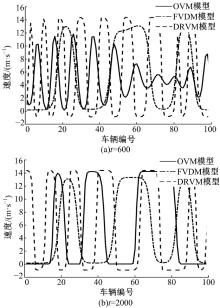	Figure Option View Download New Window
	图6 OVM, FVDM, DRVM模型的车辆速度分布Fig.6 Snapshots of velocity of all vehicles at different times according to OVM, FVDM and DRVM

图6为t=600 s和t=2000 s时刻每辆车的速度。当t=600 s时, OVM模型的车速为-0.91~14.41 m/s, 速度波动剧烈, 且出现负速度, 与实际不符。而FVDM模型的车速为0.16~12.99 m/s, DRVM模型车速变化比FVDM模型的小, 在0.14~11.48 m/s之间震荡。从图6中也可看出:与OVM和FVDM模型相比, DRVM模型的各波形相似度最小, 说明扰动在车流之间传播速度较慢。当t=2000 s时, OVM、FVDM和DRVM模型都形成触发时走时停态, 但OVM模型中仍有车辆处于负速度状态, 而FVDM和DRVM模型都能很好地表现交通拥堵时的车辆速度分布。

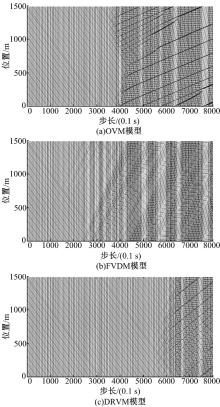
为了更好地表示交通流动态演化过程, 绘制时空图如图7所示。初始时刻交通流是均匀分布的自由流, 当t=300 s时, FVDM模型在微小扰动的影响下进入亚稳态状态, 而OVM模型则是当t=400 s时才开始进入亚稳态状态, 当t=700 s时, 二者都演变为稳定拥堵状态。与此相比较, 在DRVM模型中, 微小扰动的影响传播较慢, 直到t=600 s时才出现亚稳态, 并且在整个仿真过程中DRVM模型的拥堵程度与OVM和FVDM模型相比较轻。DRVM模型因为能够考虑驾驶员的动态反应时间, 从而在一定程度上缓解了拥堵的发生。

	Figure Option View Download New Window
	图7 OVM, FVDM, DRVM模型的时空图Fig.7 Evolution of traffic flow for OVM, FVDM and DRVM

4 结束语

根据车辆的弱跟驰、强跟驰和自由行驶3种驾驶行为, 考虑了不同间距下驾驶员对前车状态变化反应时间不同, 利用双曲正切函数建立了间距敏感系数函数; 考虑了不同间距下驾驶员对速度差敏感程度不同, 建立了速度差敏感系数函数; 结合以上两个函数, 建立了基于动态反应时间的全速度差模型(DRVM), 并进行线性稳定性分析, 得到线性稳定临界曲线。通过仿真验证了模型在车辆启动加速、车辆减速和交通状态演变下3种环境下的有效性。车辆启动加速试验表明:本文模型的启动延迟时间为1.5 s, 拥堵传播速度为17.76 km/h, 符合实际情况。在车辆减速试验中DRVM模型的减速性能与FVDM模型相比提升了25%, 安全性更高。交通状态转换试验显示, 车流中微小扰动在本文模型中传播速度比在FVDM模型降低了50%, 从一定程度缓解了交通拥堵的发生, 是对稳定交通流的有效接近。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Band o M, Hasebe K, Nakayama A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035-1042. [本文引用:1]
[2]	Helbing D. Traffic and related self-driven many-particle systems[J]. Reviews of Modern Physics, 2001, 73(4): 1067-1141. [本文引用:1]
[3]	Jiang R, Wu Q, Zhu Z. Full velocity difference model for a car-following theory[J]. Physical Review E, 2001, 64(1): 017101. [本文引用:2]
[4]	Tang T, Huang H, Wong S C, et al. A car-following model with the anticipation effect of potential lane changing[J]. Acta Mechanica Sinica, 2008, 24(4): 399-407. [本文引用:1]
[5]	Liu Y J, Zhang H L, He L. Cooperative car-following model of traffic flow and numerical simulation[J]. Chinese Physics Letters, 2012, 29(10): 104502. [本文引用:1]
[6]	Yu S, Liu Q, Li X. Full velocity difference and acceleration model for a car-following theory[J]. Communications in Nonlinear Science & Numerical Simulation, 2013, 18(5): 1229-1234. [本文引用:1]
[7]	金盛, 王殿海. 考虑前方交通状态的车辆跟驰模型与数值仿真[J]. 北京工业大学学报, 2012, 38(8): 1236-1241. Jin Sheng, Wang Dian-hai. Car following model and simulation considering front traffic situation[J]. Joural of Beijing Polytechnic University, 2012, 38(8): 1236-1241. [本文引用:1]
[8]	徐程, 曲昭伟, 金盛. 考虑侧向偏移的车辆跟驰行为建模及仿真[J]. 吉林大学学报: 工学版, 2014, 44(6): 1609-1615. Xu Cheng, Qu Zhao-wei, Jin Sheng. Modeling and simulation of car following behavior considering lateral separration[J]. Joural of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1609-1615. [本文引用:1]
[9]	Lu X, Chen W, Xu M, et al. AA-FVDM: an accident-avoidance full velocity difference model for animating realistic street-level traffic in rural scenes[J]. Computer Animation and Virtual Worlds, 2014, 25(1): 83-97. [本文引用:1]
[10]	Zhou J, Shi Z K. A modified full velocity difference model with the consideration of velocity deviation[J]. International Journal of Modern Physics C, 2016, 27(6): 1650069. [本文引用:1]
[11]	Zheng Z, Ahn S, Chen D, et al. The effects of lane-changing on the immediate follower: anticipation, relaxation, and change in driver characteristics[J]. Transportation Research Part C: Emerging Technologies, 2013, 26: 367-379. [本文引用:1]
[12]	Ota H. Distance headway behavior between vehicles from the viewpoint of proxemics[J]. IATSS Research, 1994, 18(2): 5-14. [本文引用:1]
[13]	王福建, 戴美伟, 孙凌涛, 等. 基于多类跟驰行为的车头时距混合分布模型[J]. 浙江大学学报: 工学版, 2015, 49(7): 1288-1294. Wang Fu-jian, Dai Mei-wei, Sun Ling-tao, et al. Mixed distribution model of vehicle headway based on multiclass car following[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(7): 1288-1294. [本文引用:1]
[14]	Transportation Research Board. Highway capacity manmol 2000[R]. Washington DC: National Research Council, 2001. [本文引用:2]
[15]	孟凡兴, 张良, 张伟. 驾驶员车头时距研究[J]. 工业工程与管理, 2013, 18(2): 131-135, 140. Meng Fan-xing, Zhang Liang, Zhang Wei, A study on drivers' time headway[J]. Industrial Engineering and Management, 2013, 18(2): 131-135, 140. [本文引用:1]
[16]	del Castillo J M, Benitez F G. On the functional form of the speed-density relationship-I: general theory[J]. Transportation Research Part B: Methodological, 1995, 29(5): 373-389. [本文引用:1]
[17]	Kerner B S, Rehborn H. Experimental properties of phase transitions in traffic flow[J]. Physical Review Letters, 1997, 79(20): 4030-4033. [本文引用:1]

1995

0.0

... Bando等^[1]在1995年首次提出OVM,该模型能够很好地表现交通流的相变、交通失稳特性 ...

2001

0.0

... Helbing等^[2]利用实际数据对OVM模型进行标定,并考虑负速度差的影响,对OVM模型进行扩展,提出了广义力模型 ...

2001

0.0

... Jiang等^[3]考虑了前、后两车的正负速度差,建立了全速度差模型(Full velocity difference model,FVDM),使模型更具现实性 ...

... 1 全速度差模型Jiang等^[3]考虑了前、后两车的正负速度差,建立了全速度差模型(FVDM),克服了OVM模型中出现不切实际加速度的情况,其模型结构如下: ...

2008

0.0

... Tang等^[4]考虑了双车道情况下换道车辆对跟驰行为的影响并建立了基于换道概率的跟驰模型,得出考虑前车换道概率能够增强车流运行稳定性 ...

2012

0.0

... Liu等^[5]建立了考虑后车期望速度和安全间距的跟驰模型,该模型能够克服FVDM模型中会出现负速度的缺点 ...

2013

0.0

... Yu等^[6]将前车加速度引入到FVDM模型中,避免了FVDM模型中后车出现加速度过高的现象 ...

2012

0.0

. 2012, 38(8):1236-1241

Car following model and simulation considering front traffic situation

考虑前方交通状态的车辆跟驰模型与数值仿真

Jin Sheng , Wang Dian-hai.

金盛, 王殿海

... 金盛等^[7]在FVDM模型基础上考虑前方交通状态,更加实际地描述了前方多辆车对驾驶行为的影响 ...

2014

0.0

. 2014, 44(6):1609-1615

Modeling and simulation of car following behavior considering lateral separration

考虑侧向偏移的车辆跟驰行为建模及仿真

Xu Cheng , Qu Zhao-wei , Jin Sheng.

徐程, 曲昭伟, 金盛

... 徐程等^[8]建立了考虑车辆驾驶过程侧向偏移的跟驰模型,得出侧向偏移会降低交通流稳定性 ...

2014

0.0

... Lu等^[9]建立了基于现实水平的三维交通流仿真模型,在模型中引入避免碰撞的全速度差模型,并利用实际数据对仿真模型进行验证,取得较好的效果 ...

2016

0.0

... Zhou等^[10]考虑了车辆跟驰行为中驾驶员对于自身速度估计过高或过低的现象,建立了基于速度分布的优化速度模型,并得出驾驶员对于自身速度估计偏大时更有利于交通流稳定 ...

2013

0.0

... Zheng等^[11]研究了换道行为对换道车驾驶员特性的影响,得出驾驶员在换道前后驾驶特性会发生变化 ...

1994

0.0

... Ota^[12]的驾驶试验证明不同驾驶员在相同条件下也会选择不同的车头时距 ...

2015

0.0

. 2015, 49(7):1288-1294 DOI:doi:10.3785/j.issn.1008-973X.2015.07.013

Mixed distribution model of vehicle headway based on multiclass car following

基于多类跟驰行为的车头时距混合分布模型

Wang Fu-jian , Dai Mei-wei , Sun Ling-tao

王福建, 戴美伟, 孙凌涛

摘　要：基于实际的驾驶行为特性,将驾驶员的驾驶状态分为强跟驰、弱跟驰和自由流3种状态,建立能够描述这3种状态的车头时距三元混合分布模型.利用北京快速路实测数据,通过最大期望（EM）算法标定了三元混合分布模型中的参数,对3种不同驾驶行为数据进行分析.通过研究对比各个车头时距分布模型的拟合精度,结果表明,提出的车头时距混合模型的拟合结果优于威布尔分布以及对数正态分布模型.

... 王福建等^[13]的研究表明:驾驶员跟驰过程中存在强跟驰和弱跟驰状态,强跟驰时,前、后车间距较小,后车根据前车状态迅速调整自身速度 ...

2001

0.0

... 2 DRVM模型HCM2000定义双车道公路车头时距大于5 s时车辆为自由行驶状态,前车状态不会对后车产生影响^[14] ...

... 根据文献^[14],车辆弱跟驰时,车头间距较大,反应时间长,取 κ1=0 ...

2013

0.0

. 2013, 18(2):131-135,140 DOI:doi:10.3969/j.issn.1007-5429.2013.02.021

A study on drivers' time headway

驾驶员车头时距研究

Meng Fan-xing , Zhang Liang , Zhang Wei

孟凡兴, 张良, 张伟

车头时距是评价驾驶员驾驶安全性的重要指标。本研究针对驾驶员在驾驶中保持的车头时距提出了一种新的理论框架,将车辆跟驰状态分成两类:强跟驰和弱跟驰。处于强跟驰状态时,驾驶员保持最短车头时距;处于弱跟驰状态时,驾驶员保持舒适车头时距,即在最短车头时距的基础上预留出一定的心理裕量。根据大量车头时距的实测数据,本研究对理论框架的有效性进行验证。结果表明,本研究提出的理论框架能够较好地解释车头时距的实测数据,最短车头时距和舒适车头时距分别满足以1.55秒和2.60秒为均值,以0.48秒和1.13秒为标准差的正态分布,而车头时距的实测数据可以由这两个正态分布的混合分布来拟合。

1995

0.0

... 3 环路仿真Kerner等^[16]的研究认为在实际交通中存在自由流、同步流和宽运动阻塞3种状态,而后两者也属于拥堵状态 ...

1997

0.0