在数据准备阶段, 对待选指标的原始数据进行离差标准化处理, 使结果落到[0, 1]区间, 定性、定量地进行聚类分析, 处理后的数据为向量集合的形式。

设有n个待选指标X_n, 每个指标包含m个特征数据, 记每个特征数据经过离差标准化后的数据为x_n(m), 记为X_n=(x_n(1), x_n(2), …, x_n(m))。

对所有的i≤ j, i, j=1, 2, …, m, 计算出x_i与x_j的关联系数^[10]ξ _ij(m), 如式(1)所示:

ξij(m)=Δmin(m)+ρ·Δmax(m)|xi(m)-xj(m)|+ρ·Δmax(m)1

式中:Δ _min(m)=min min|x_i(m)-x_j(m)|; Δ _max(m)= maxmax|x_i(m)-x_j(m)|; minmin|x_i(m)-x_j(m)|为两级最小差; maxmax|x_i(m)-x_j(m)|为两级最大差; 分辨系数ρ 越大, 分辨率越小, 通常取0.5为最优, 灰色系统理论取关联系数ξ _i(n)的均值作为序列X_i与X_j的关联系数r_ij, 如式(2)所示:

rij=1k∑n=1kξij(m)(2)

根据式(1)(2)可计算出n个指标之间的关联系数, 由各关联系数构成评价指标体系的n× n阶关联度矩阵R_{n× n}, 即:

R_{n× n}= r11r12…r1nr22…r2n⋱︙rnn

采用一次形成聚类结构算法^[11]完成指标聚类, 其步骤为:选取两个指标, 若都不属于已分好的组, 则归为一个独立分组; 若一个出现在已有的组中, 则不分组; 若分别属于已有的两个分组中, 则把这两个组合并; 若都出现在同一组中, 则不再分组, 如此反复操作, 直至全部待选指标聚类完成。

粗糙集理论^[12]是由波兰的Pawlak于1982年提出的一种处理含糊和不精确数据的方法, 其主要特点是无需使用隶属度函数或对属性的描述, 直接从给定数据的分类知识出发, 通过不可分辨关系确定给定数据的知识约简。

定义1 信息系统可表示为S=(U, A, V, f), U为对象的有限集; A为有限属性集, A=C∪ D, C为条件属性子集, D为决策属性子集; V为属性值组成的集合, 指定U中每一个对象的属性值, 即f:U× A→ V。

设∀ P⊂A, 不可分辨关系IND(P)为IND(P)={(x, y)∈ U²|∀ a∈ P, x≠ y, f(x, a)=f(y, a)}, IND(P)构成了U的一个划分, 用U/IND(P)表示, 简记为U/P={x₁, x₂, …, x_k}。

设R⊂A, r∈ R, 当IND(R)=IND(R-{r})时, 称r是R中不必要的^[13]; 否则称r是R中必要的。若每个r∈ R都是R中必要的, 则称R为独立的。假设Q∈ R, 若Q是独立的, 并且IND(P)=IND(Q), 则称Q为论域U在属性集P上的约简。

2.1.1 三角模糊数的概念

定义2 设 M~ij=(l_ij, m_ij, μ _ij)为三角模糊数^[14], 其中0< l_ij< m_ij< μ _ij, l_ij和μ _ij分别为 M~ij的下界和上界, m_ij为 M~ij的中值, 其隶属度函数为:

μM~ij=(x-a)(b-a), x∈a, b(x-c)(b-c), x∈b, c0, 其他3

式中:a< b< c, {x∈ R|1< x< c}。

2.1.2 模糊互补判断矩阵建立

定义3 设判断矩阵 M~= (M~ij)n×n, 三角模糊数 M~ij=(l_ij, m_ij, μ _ij), 若满足:①l_ii=m_ii=μ _ii=0.5, ②l_ij+μ _ji=m_ij+m_ji=μ _ij+l_ji=1, i≠ j, ∀ i、j, 则称 M~为三角模糊互补判断矩阵^[15]。

互补判断矩阵的作用是在上一层某指标的约束条件下, 对同层元素之间的相对重要性进行比较; 判断矩阵采用模糊DELPHI法获得^[16], 设三角模糊互补判断矩阵 A~= a~ijn×n, 其中三角模糊数 aij~=(l_ij, m_ij, μ _ij), μ _ij≥ m_ij≥ l_ij, i, j∈ N。 aij~表示第i个因素与第j个因素的重要程度之比。请t位专家打分, 判断矩阵的各个元素根据式(4)求出:

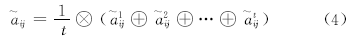
式中: a~ijt为第t位专家给出的第i行第j列因素的三角模糊数形式, t∈ N。

先求出单层次指标的权重, 从而获得各指标相对于目标层的权重, 设对应于上层次某指标的指标个数为n, 由式(5)计算出第i个指标相对于上一层某指标的三角模糊权重向量 W~=( w~1, w~2, …, w~n)。

w~i=∑j=1na~ij∑k=1n∑j=1na~ij= ∑j=1nlij, ∑j=1nmij, ∑j=1nμij ∑k=1n∑j=1nlij, ∑k=1n∑j=1nmij, ∑k=1n∑j=1nμij5i=1, 2, …, n

经归一化处理得一级指标权重记为 W~'=( w~'₁, w~'₂, …, w~'_n), n∈ N, 同理可求出二级指标相对于一级指标的权重值 W~″。

本试验招募了30名(男18名, 女12名)具有合法驾驶执照的驾驶人, 年龄为23~49岁(均值29岁), 驾龄为2~13年(均值5年), 该年龄段人群是驾驶人数量最多的人群, 也是使用手机、蓝牙设备等最多、最活跃的人群, 具有代表性。

驾驶人眼动行为采集设备由SmartEye6.0型眼动追踪系统搭配4台眼动行为追踪摄像头组成, 4台眼动行为追踪相机则主要负责驾驶人眼动行为的采集和保存。

车辆运行状态信息采集系统以奔腾B50型车为载体, 车内嵌入道路场景模拟仿真系统、数据采集系统等部分。驾驶场景模拟长春市至吉林市高速公路路段。

眼动仪可以采集扫视速度均值、扫视速度标准差等8种参数; 驾驶模拟器可以采集油门开度均值等9种参数, 共组成待选指标17种, 分别用于分析眼动行为状态和车辆运行状态。

试验要求每名驾驶人控制车速在60~120 km/h, 并选取蓝牙耳机通话、手持电话通话、发信息、调整车载音乐播放器、交谈及唱歌作为驾驶次任务。具体试验方法如下:

(1)蓝牙通话。试验者使用蓝牙耳机与试验助理接打电话, 通话内容为试验助理向驾驶人询问简单问题15次。

(2)手持通话。试验者与试验助理使用手持电话通话, 通话内容为试验助理询问试验者简单问题15次。

(3)发信息(短信或微信)。试验者与试验助理发信息, 回答简单问题10次。

(4)使用音乐播放设备。试验者操作车载音乐播放器, 听试验助理指挥, 相继切换5首歌曲并适当调节音量。

(5)交谈。试验者回答试验助手15个简单问题。

(6)唱歌。试验者唱一首自己熟悉的歌曲, 持续2 min。

本文以30名试验者的眼动状态参数、车辆状态参数为样本, 使用SPSS软件对原始数据进行统计分析并计算标准差, 然后依据式(6)进行离差标准化处理^[17], 表1为经离差标准化后的数据。

x'=x-xminxmax-xmin6

式中:x为样本数据; x_min、x_max分别为样本数据的最小值和最大值; x'为经过离差标准化后的数值。

表1

Table 1

表1(Table 1)

表1 经离差标准化处理后的数据 Table 1 Data after normalization 待选指标 驾驶任务类型 蓝牙通话 手持通话 发信息 播放音乐 交谈 唱歌 眼动状态参数 扫视速度均值 0.233 0.240 0.177 0.238 0.221 0.280 扫视速度标准差 0.302 0.286 0.239 0.167 0.269 0.362 眨眼频率均值 0.160 0.219 0.272 0.252 0.152 0.192 眨眼频率标准差 0.166 0.251 0.151 0.070 0.125 0.149 扫视速度峰值 0.137 0.224 0.169 0.221 0.130 0.151 扫视速度峰值标准差 0.162 0.139 0.151 0.088 0.151 0.178 眨眼持续时间均值 0.300 0.172 0.107 0.226 0.285 0.314 眨眼持续时间标准差 0.221 0.292 0.184 0.120 0.210 0.189 车辆状态参数 油门开度均值 0.234 0.160 0.260 0.208 0.225 0.202 油门开度标准差 0.249 0.152 0.151 0.130 0.237 0.331 纵向加速度标准差 0.169 0.181 0.207 0.188 0.152 0.144 方向盘转角均值 0.159 0.103 0.155 0.226 0.140 0.168 方向盘转角标准差 0.258 0.115 0.229 0.216 0.227 0.225 纵向速度均值 0.259 0.209 0.289 0.212 0.246 0.369 纵向速度标准差 0.188 0.278 0.241 0.098 0.179 0.214 横向加速度均值 0.152 0.204 0.238 0.139 0.221 0.280 横向加速度标准差 0.191 0.166 0.134 0.199 0.269 0.362

表1 经离差标准化处理后的数据 Table 1 Data after normalization

使用式(1)(2)计算表1数据得到灰色关联矩阵R_{6× 6}为:

R6×6=10.6340.7090.6090.7990.75810.5520.6590.6430.71010.6640.6820.69310.6920.70510.6461

设论域U=(x₁, x₂, …, x₆), 论域内各元素x_i分别为各种类型的驾驶次任务, 每个x_i内包含j个数据, 即x_i=(x_i1, x_i2, …, x_ij), j=1, 2, …, 17。各评价指标用C_j表示, C_ji=x_ij。应用一次形成聚类结构算法^[18], 结合粗糙集理论中^[19]指标划分论域算法, 分类情况为:

X=U/C={{x2, x4}, {x1, x5, x6, x3}}

根据此分类应用粗糙集理论约简指标得:U/(C-C₈)=U/(C-C₁₁)=U/(C-C₃)=

U/(C-C₁₅)=U/(C-C₁₂)=U/(C-C₄)=

U/(C-C₇)=U/(C-C₉)={{x₂, x₄}, {x₁, x₅, x₆, x₃}};

U/(C-C₁)=U/(C-C₁₄)={{x₂, x₄, x₅}, {x₁, x₆, x₃}};

U/(C-C₂)={{x₂, x₄}, {x₁, x₅}, {x₆, x₃}};

U/(C-C₅)={{x₂, x₄}, {x₁, x₃, x₅}, {x₆}};

U/(C-C₆)={{x₁, x₅, x₆}, {x₂, x₃, x₄}};

U/(C-C₁₀)={{x₄}, {x₁}, {x₂, x₃, x₅, x₆}};

U/(C-C₁₃)={{x₂, x₃, x₄}, {x₁, x₅, x₆}}。

则指标C₃, C₄, C₇, C₈, C₉, C₁₁, C₁₂, C₁₅约简后不影响分类结果, 属于不必要的指标。C₁和C₁₄分别属于眼动行为状态和车辆运行状态, 故两个指标都保留, 可得约简后的评价指标体系为最小属性集{C₁, C₂, C₅, C₆, C₁₀, C₁₃, C₁₄}。

将专家小组给出的判断矩阵转换成三角模糊数形式, 同时用于专家评判的两个指标分别记为i和j; B₁、B₂分别表示眼动行为参数和车辆状态参数, 模糊判断矩阵标度如表2所示, 一级指标对总目标的模糊判断矩阵如表3所示。

表2

Table 2

表2(Table 2)

表2 模糊判断矩阵标度赋值表 Table 2 Fuzzy judgmental matrix scale assignment 标度值 含义 标度值 含义 0.9 i比j极端重要 0.4 i比j稍微不重要 0.8 i比j强烈重要 0.3 i比j明显不重要 0.7 i比j明显重要 0.2 i比j强烈不重要 0.6 i比j稍微重要 0.1 i比j极端不重要 0.5 i与j同样重要

表2 模糊判断矩阵标度赋值表 Table 2 Fuzzy judgmental matrix scale assignment

表3

Table 3

表3(Table 3)

表3 一级指标模糊判断矩阵 Table 3 Fuzzy judgmental matrix of first order indexes 模糊判断矩阵 B1 B2 B1 1 1 1 5/2 3 7/2 B2 2 7/3 8/3 1 1 1

表3 一级指标模糊判断矩阵 Table 3 Fuzzy judgmental matrix of first order indexes

根据式(5)计算并归一化得到一级指标权重向量为 W~'=(0.596, 0.404)。同理, 可求各二级指标相对于一级指标的权重值W″_i如表4所示。

表4

Table 4

表4(Table 4)

表4 次任务驾驶综合评价指标权重 Table 4 Comprehensive evaluation index weight of secondary task driving 一级指标 权重 二级指标 权重 眼动行为状态 0.596 扫视速度均值 0.291 扫视速度标准差 0.242 扫视速度峰值 0.205 扫视速度峰值标准差 0.178 车辆运行状态 0.404 油门开度标准差 0.435 方向盘转角标准差 0.350 纵向速度均值 0.215

表4 次任务驾驶综合评价指标权重 Table 4 Comprehensive evaluation index weight of secondary task driving

本试验共采集17种待选指标, 应用灰色粗糙集理论约简至眼动行为状态指标4种、车辆运行状态指标3种, 建立了共7种指标的约简评价指标体系。

眼动行为指标的二级指标按重要程度从高到低排序依次为:扫视速度均值、扫视速度标准差、扫视速度峰值、扫视速度峰值标准差。

车辆运行状态的二级指标按重要程度从高到低排序依次为:油门开度标准差、方向盘转角标准差、纵向速度均值。

从表4可知, 一级指标中的眼动行为状态权重大于车辆运行状态权重, 表明眼动行为状态指标比车辆运行状态指标更能反映驾驶安全性。