对向行人流均衡反馈控制模型

引用本文

张蜇, 贾利民, 秦勇, 云婷. 对向行人流均衡反馈控制模型[J].吉林大学学报（工学版）, 2017,47(6): 1728-1737
ZHANG Zhe, JIA Li-min, QIN Yong, YUN Ting. Equalization-based feedback control model of pedestrian counter flow[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1728-1737 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706008
Permissions

对向行人流均衡反馈控制模型

张蜇¹, 贾利民^1,^2,³, 秦勇^1,^2,³, 云婷^1,^2,³

1.北京交通大学轨道交通控制与安全国家重点实验室,北京 100044

2.北京交通大学交通运输学院,北京 100044

3.北京交通大学北京市城市交通信息智能感知与服务工程技术研究中心,北京 100044

通讯作者：贾利民(1963-),男,教授,博士生导师.研究方向:交通控制与安全.E-mail:jialm@vip.sina.com

作者简介:张蜇(1988-),男,博士研究生.研究方向:交通运输规划与管理.E-mail:13114245@bjtu.edu.cn

基金:“十三五”国家重点研发计划项目(2017YFB1201200); 国家自然科学基金项目(71171015)

摘要

为避免双向通道行人流堵塞,建立了对向行人流反馈控制模型。考虑了对向行人流的干扰特性,利用社会力模型的匀速条件推导了对向行人流基本图。由于行人密度沿通道分布不同,按照行走方向不同,将双向通道分为多个分通道,采用状态空间方程建立了基于行人流量守恒的对向行人流系统动力学模型。为满足对向行人移动需求,提出对向行人流均衡控制目标,并建立了线性反馈控制模型。该模型可通过实时调整行人速度和通道两端的行人流入量,使得通道行人密度收敛于临界密度,从而最大化通道行人流量,提高通道服务水平。本文模型可以作为解决行人流和道路交通实时控制问题的普适方法。

关键词: 交通运输系统工程; 对向行人流; 系统动力; 反馈控制

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2017)06-1728-10

Equalization-based feedback control model of pedestrian counter flow

ZHANG Zhe¹, JIA Li-min^1,^2,³, QIN Yong^1,^2,³, YUN Ting^1,^2,³

1.State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China

2.Traffic and Transportation School, Beijing Jiaotong University, Beijing 100044, China

3.Beijing Research Center of Urban Traffic Information Sensing and Service Technologies, Beijing Jiaotong University,Beijing 100044, China

Abstract

A feedback control model of pedestrian counter flow was established to avoid pedestrian flow blocking in bidirectional corridors. The fundamental diagram of bidirectional pedestrian flow incorporating the conflict characteristic was derived using the social force model under the uniform state. To accommodate the possible inhomogeneous pedestrian density along the corridor, the bidirectional corridor was divided into several sections for different directions. A system dynamics model of pedestrian counter flow was proposed using the conversation law of pedestrian mass and the state space equation. To satisfy the moving demand of pedestrians in both directions, the equalization control objective was proposed based on the user equilibrium theory, and the linear feedback control model was established. The proposed control model can maximize the output flow of the corridor, thus improving the service level of the corridor by adjusting the walking speed of pedestrians and the corridor input flow in real time. The proposed model has the capability to serve as a general control method of both pedestrian flow and vehicle flow.

Keyword: engineering of communication and transportation system; pedestrian counter flow; system dynamics; feedback control

Show Figures

0 引言

目前, 大型行人集散设施(如地铁站, 机场, 大型商场等)正向着信息化、智能化方向发展, 通过在一些重点区域和位置装设摄像头、传感器等感知设备监测行人流动^[1], 并通过无线网络传输设备, 管理人员可以获得某一区域行人流的基本信息(如速度、密度和流量等), 这为行人流的智能控制提供了数据来源和技术支持。根据集散设施内行人流动的方向, 可以将行人流分为单向行人流、对向行人流和交叉行人流3类。对向行人流是指在一条双向通道内同时存在两个向相反方向行走的行人流现象, 相比于单向行人流, 由于不同方向的行人流之间存在强烈正面冲突和交叉冲突^[2], 对向行人流中行人之间的相互影响更甚, 堵塞的概率也会更高。因此, 对向行人流的控制更具实际意义。

通道内的对向行人流作为一种常见现象, 对其的研究也较为广泛。目前对向行人流模型主要分为微观模型和宏观模型。社会力模型^[3]、元胞自动机模型^[4]、格子气模型^[5]等在内的微观仿真模型将行人看作离散的个体, 通过模拟个体行为体现群体动力学特征, 这些微观模型凭借模型简单、容易编程等优点, 成为研究对向行人流的一类重要模型。微观模型在模拟行人流各种现象(如行人超越^[6]、冲突和吸引^{[7, 8]}、行人偏走^[9]、随机分层^{[10, 11]}和对向行人冲突所致的死锁堵塞现象^[12]等)方面具有一定优势。在行人流控制方面, 文献[13]基于元胞自动机模型, 模拟建立了行人与疏导员之间的微观交互过程, 得出单个房间内疏导员的最优位置和数量, 以提高疏散效率。文献[14]基于格子气模型, 发现对向行人流间设置分割线可以有效提高双向行人流的流量。文献[15]基于社会力模型, 发现行人期望速度越高, 疏散时间反而越长, 并且存在使疏散时间最短的行人期望速度。文献[16]发现通过调整行人尺寸、反应时间和期望速度, 可以影响对向行人流的堵塞发生概率和起始时间。文献[17-20]基于格子气数值分析和模拟验证, 发现行人记忆依赖程度、横向移动舒适度、心理预期和密度差会影响双向行人流的稳定性。微观模型可以再现对向行人流自组织现象, 其控制策略涵盖了行人心理、生理以及环境结构等多方面因素, 具备多样性特点, 但由于微观模型仿真颗粒度小, 其计算时间也随着群体数量和行人移动规则的增多而快速增长, 而且难以构建解析方法求解行人流的最优控制策略。因此, 微观模型适用于小规模行人群体动力学建模, 只有具备强大的计算性能或者准确的解析等价模型, 微观模型才能适用于行人流的实时控制和管理。

宏观模型将行人群体视作连续流体, 通常采用偏微分方程描述行人群体的移动行为, 此类模型包括一维^[21]和二维流体力学(LWR)模型^{[22, 23]}, 相对于微观模型, 宏观模型的行人群体模拟时间较少^[24], 非常适于大规模行人群体的系统动力学建模和实时控制^{[25, 26]}。目前, 基于宏观模型的车流控制研究较多^{[27, 28, 29, 30, 31, 32, 33]}, 行人流控制研究主要集中在疏散过程中的单向行人流控制^{[34, 35, 36, 37]}, 而关于冲突更为严重的对向行人流的控制研究较少, 这在一定程度上减缓了行人集散设施智能化发展进程。与单向行人流控制不同, 对向行人流控制不仅要考虑系统最优, 而且要平衡不同方向行人的移动需求。

因此, 本文首先根据行人微观模型推导对向行人流基本图, 实现了微观行人移动和宏观行人流现象的统一; 考虑对向行人流之间的干扰, 建立了基于流量守恒的对向行人流系统动力学模型, 采用状态方程形式描述了对向行人流演变过程。然后, 基于用户平衡和系统最优原则, 提出了对向行人流动力系统的均衡反馈控制模型和求解算法。最后, 将本文模型应用于对向行人流控制中, 证明本文模型可以为行人流的智能控制和管理提供理论支持。

1 对向行人流系统动力学模型

1.1 对向行人流基本图

建立对向行人流系统动力学模型的前提是清楚描述对向行人流基本图, 即行人流速度、密度和流量三者间的关系。Nikoli $\begin{matrix} \overset{'}{c} \end{matrix}$ 根据社会力模型中加速度的不同表现形式和行人匀速的假设推导出了各种单向行人流基本图^[38], 其中Greenshields基本图^[39]推导过程如下。

根据社会力模型, 行人 $\begin{matrix} p \end{matrix}$ 的加速度 $\begin{matrix} a_{p} \end{matrix}$ 为:

$\begin{matrix} a_{p} = \frac{v_{m}^{f} - v_{p}}{τ} - F_{p} (1) \end{matrix}$

式中: $\begin{matrix} v_{m}^{f} \end{matrix}$ 为行人期望速度; $\begin{matrix} v_{p} \end{matrix}$ 为行人当前速度; $\begin{matrix} τ \end{matrix}$ 为行人加速时间; $\begin{matrix} F_{p} \end{matrix}$ 为其他行人对行人的总作用力, 并且与行人 $\begin{matrix} p \end{matrix}$ 所处区域的密度 $\begin{matrix} ρ_{p} \end{matrix}$ 和期望速度成正比。假设 $\begin{matrix} F_{p} = S_{p} v_{m}^{f} ρ_{p} / ρ_{m}, ρ_{m} 为堵塞密度, S_{p} \end{matrix}$ 为行人 $\begin{matrix} p \end{matrix}$ 与其他行人之间的拥挤作用强度^[15], 令 $\begin{matrix} S_{p} = 1 / τ, \end{matrix}$ 当行人匀速运动时, 令 $\begin{matrix} a_{p} = 0, \end{matrix}$ 得:

$\begin{matrix} v_{p} = v_{m}^{f} (1 - ρ_{p} / ρ_{m}) (2) \end{matrix}$

将式(2)应用于所有行人, 可得Greenshields单向行人流基本图模型为:

$\begin{matrix} v = v_{m}^{f} (1 - ρ / ρ_{m}) (3) \end{matrix}$

对于交叉行人流, 行人所受作用力不仅具有单向行人流中拥挤力 $\begin{matrix} F_{p}, \end{matrix}$ 更有异向行人的冲突力 $\begin{matrix} F_{c}, \end{matrix}$ 令冲突强度为 $\begin{matrix} α, 0 \leq α \leq 1, \end{matrix}$ 表示异向行人流中对行人 $\begin{matrix} p \end{matrix}$ 有冲突作用的人数所占比例; 令 $\begin{matrix} φ \end{matrix}$ 为不同方向行人流之间夹角。在交叉行人流中, 令 $\begin{matrix} {ρ^{c}}_{p} \end{matrix}$ 为异向行人流密度, 根据 $\begin{matrix} F_{p} \end{matrix}$ 的表达形式, 令 $\begin{matrix} F_{c} = (1 - cosφ) S_{p} v_{p} α {ρ^{c}}_{p} / ρ_{m} = α S_{p} v_{m}^{f} {ρ^{c}}_{p} / ρ_{m} (1 - ρ_{p} / ρ_{m}) (1 - cosφ) 。 \end{matrix}$ 对于单向行人流, $\begin{matrix} cosφ = 1, \end{matrix}$ 无冲突作用力; 对于对向行人流, $\begin{matrix} cosφ = - 1, \end{matrix}$ 行人冲突最为严重, $\begin{matrix} F_{c} = S_{p} v_{p} α {ρ^{c}}_{p} / ρ_{m} = 2 α S_{p} v_{m}^{f} {ρ^{c}}_{p} / ρ_{m} (1 - ρ_{p} / ρ_{m}) 。 \end{matrix}$ 那么:

$\begin{matrix} \begin{matrix} a_{p} = \frac{v_{m}^{f} - v_{p}}{τ} - v_{m}^{f} S_{p} ρ_{p} / ρ_{m} - \\ 2 v_{m}^{f} S_{p} α {ρ^{c}}_{p} / ρ_{m} (1 - ρ_{p} / ρ_{m}) (4) \end{matrix} \end{matrix}$

同样, 令 $\begin{matrix} a_{p} = 0, S_{p} = 1 / τ \end{matrix}$ 并具体到右向行人速度 $\begin{matrix} v^{r} \end{matrix}$ 和左向行人速度 $\begin{matrix} v^{l}, \end{matrix}$ 得到对向行人流基本图, 如式(5)所示:

$\begin{matrix} \{\begin{matrix} v^{r} = v_{m}^{f} (1 - ρ / ρ_{m}) (1 - 2 α ρ^{l} / ρ_{m}) \\ v^{l} = v_{m}^{f} (1 - ρ / ρ_{m}) (1 - 2 α ρ^{r} / ρ_{m}) \end{matrix} (5) \end{matrix}$

式中: $\begin{matrix} ρ^{r} 、 ρ^{l} \end{matrix}$ 分别为右向行人和左向行人密度; $\begin{matrix} ρ = ρ^{r} + ρ^{l}; α = 0 \end{matrix}$ 表示无冲突情形, 对向行人流完全分离, 此时式(5)与式(3)一致, $\begin{matrix} α = 1 \end{matrix}$ 为完全冲突情形, 此时两个方向的行人流完全交叉。

将所得对向行人流基本图与文献[40]结果比较, 尽管两者基于的单向行人流基本图不同, 但两者最终表达形式基本相同, 从而验证本文推导过程的正确性。

右向行人流量 $\begin{matrix} q^{r} \end{matrix}$ 和左向行人流量 $\begin{matrix} q^{l} \end{matrix}$ 分别为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} q^{r} = ρ^{r} v_{m}^{f} (1 - ρ / ρ_{m}) (1 - 2 α ρ^{l} / ρ_{m}) \\ q^{l} = ρ^{l} v_{m}^{f} (1 - ρ / ρ_{m}) (1 - 2 α ρ^{r} / ρ_{m}) \end{matrix} \\ (6) \end{matrix} \end{matrix}$

并且, 当 $\begin{matrix} ρ^{r} = \frac{ρ_{m} - ρ^{l}}{2}, ρ^{l} = \frac{ρ_{m} - ρ^{r}}{2} \end{matrix}$ 时, $\begin{matrix} q^{r} 、 q^{l} \end{matrix}$ 分别取得最大值 $\begin{matrix} q_{m}^{r} 和 q_{m}^{l} : \end{matrix}$

$\begin{matrix} \{\begin{matrix} q_{m}^{r} = \frac{ρ_{m} - ρ_{l}}{4} v_{m}^{f} (1 - \frac{ρ_{l}}{ρ_{m}}) (1 - 2 α \frac{ρ_{l}}{ρ_{m}}) \\ q_{m}^{l} = \frac{ρ_{m} - ρ_{r}}{4} v_{m}^{f} (1 - \frac{ρ_{r}}{ρ_{m}}) (1 - 2 α \frac{ρ_{r}}{ρ_{m}}) \end{matrix} (7) \end{matrix}$

1.2 对向行人流动力学模型

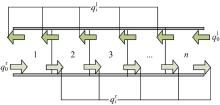
令双向通道长度为L, 将通道分为n个分通道, 如图1所示, 分通道i的长度为L_i 。对于右向行人流, 令 $\begin{matrix} {q^{r}}_{0} \end{matrix}$ 为通道左向行人瞬时流入量, $\begin{matrix} {q^{r}}_{i} \end{matrix}$ 为分通道 $\begin{matrix} i \end{matrix}$ 右向瞬时行人流出量; $\begin{matrix} {ρ^{r}}_{i} \end{matrix}$ 为分通道 $\begin{matrix} i \end{matrix}$ 右向行人密度。对于左向行人流, 令 $\begin{matrix} {q^{l}}_{0} \end{matrix}$ 为通道右向行人瞬时流入量, $\begin{matrix} {q^{l}}_{i} \end{matrix}$ 为分通道 $\begin{matrix} i \end{matrix}$ 左向瞬时行人流出量; $\begin{matrix} {ρ^{l}}_{i} \end{matrix}$ 为分通道 $\begin{matrix} i \end{matrix}$ 左向行人密度, $\begin{matrix} ρ_{i} = {ρ^{r}}_{i} + {ρ^{l}}_{i} \end{matrix}$ 为分通道 $\begin{matrix} i \end{matrix}$ 的行人密度。

	Figure Option View Download New Window
	图1 模型变量Fig.1 Variables used in model

根据连续流体力学LWR(Lighthill_Whithom_Richards)模型, 每个分通道右向和左向行人流均遵循以下公式:

$\begin{matrix} \{\begin{matrix} \frac{\partial {ρ^{r}}_{i}}{\partial t} + \frac{\partial {q^{r}}_{i}}{\partial x} = 0 \\ \frac{\partial {ρ^{l}}_{i}}{\partial t} + \frac{\partial {q^{l}}_{i}}{\partial x} = 0 \end{matrix} (8) \end{matrix}$

假设每个分通道行人密度均匀分布, 根据式(8), 对于右向和左向行人流分别有:

$\begin{matrix} \begin{matrix} \{\begin{matrix} \frac{{ρ^{r}}_{i} (t + Δt) - {ρ^{r}}_{i} (t)}{Δt} - \frac{{q^{r}}_{i - 1} - {q^{r}}_{i}}{L_{i}} = 0 \\ \frac{{ρ^{l}}_{i} (t + Δt) - {ρ^{l}}_{i} (t)}{Δt} - \frac{{q^{l}}_{i + 1} - {q^{l}}_{i}}{L_{i}} = 0 \end{matrix} (9) \\ 令 : Δ {ρ^{r}}_{i} = {ρ^{r}}_{i} (t + Δt) - {ρ^{r}}_{i} (t) \\ Δ {ρ^{l}}_{i} = {ρ^{l}}_{i} (t + Δt) - {ρ^{l}}_{i} (t) \end{matrix} \end{matrix}$

那么分通道 $\begin{matrix} i \end{matrix}$ 的右向和左向行人流的流量守恒方程分别为:

$\begin{matrix} \{\begin{matrix} Δ {ρ^{r}}_{i} L_{i} = ({q^{r}}_{i - 1} - {q^{r}}_{i}) Δt \\ Δ {ρ^{l}}_{i} L_{i} = ({q^{l}}_{i + 1} - {q^{l}}_{i}) Δt \end{matrix} (10) \end{matrix}$

令 $\begin{matrix} Δt \to 0, \end{matrix}$ 那么:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{{ρ^{r}}_{i}} = \frac{({q^{r}}_{i - 1} - {q^{r}}_{i})}{L_{i}} \\ \overset{\cdot}{{ρ^{l}}_{i}} = \frac{({q^{l}}_{i + 1} - {q^{l}}_{i})}{L_{i}} \end{matrix} (11) \end{matrix}$

式中: $\begin{matrix} “ \cdot ” \end{matrix}$ 为求导运算符, $\begin{matrix} \overset{\cdot}{{ρ^{r}}_{i}} \end{matrix}$ 和 $\begin{matrix} \overset{\cdot}{{ρ^{l}}_{i}} \end{matrix}$ 分别表示 $\begin{matrix} {ρ^{r}}_{i} \end{matrix}$ 和 $\begin{matrix} {ρ^{l}}_{i} 关于时间 t \end{matrix}$ 的导数。

将式(6)代入式(11)得:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{{ρ^{r}}_{i}} = [{ρ^{r}}_{i - 1} {v^{r}}_{i - 1} (1 - \frac{ρ_{i - 1}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{l}}_{i - 1}}{ρ_{m}}) - \\ {ρ^{r}}_{i} {v^{r}}_{i} (1 - \frac{ρ_{i}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{l}}_{i}}{ρ_{m}})] / L_{i} \\ \overset{\cdot}{{ρ^{l}}_{i}} = [{ρ^{l}}_{i + 1} {v^{l}}_{i + 1} (1 - \frac{ρ_{i + 1}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{r}}_{i + 1}}{ρ_{m}}) - \\ {ρ^{l}}_{i} {v^{l}}_{i} (1 - \frac{ρ_{i}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{r}}_{i}}{ρ_{m}})] / L_{i} \end{matrix} (12) \end{matrix}$

式中: $\begin{matrix} {v^{r}}_{i} \end{matrix}$ 和 $\begin{matrix} {v^{l}}_{i} \end{matrix}$ 分别为分通道 $\begin{matrix} i \end{matrix}$ 右向和左向行人的控制速度。

将式(12)两端同时除以 $\begin{matrix} ρ_{m} \end{matrix}$ 得:

$\begin{matrix} \{\begin{matrix} \frac{\overset{\cdot}{{ρ^{r}}_{i}}}{ρ_{m}} = \\ \frac{\frac{{ρ^{r}}_{i - 1}}{ρ_{m}} {v^{r}}_{i - 1} (1 - \frac{ρ_{i - 1}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{l}}_{i - 1}}{ρ_{m}}) - \frac{{ρ^{r}}_{i}}{ρ_{m}} {v^{r}}_{i} (1 - \frac{ρ_{i}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{l}}_{i}}{ρ_{m}})}{L} \frac{L}{L_{i}} \\ \frac{\overset{\cdot}{{ρ^{l}}_{i}}}{ρ_{m}} = \\ \frac{\frac{{ρ^{l}}_{i + 1}}{ρ_{m}} {v^{l}}_{i + 1} (1 - \frac{ρ_{i + 1}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{r}}_{i + 1}}{ρ_{m}}) - \frac{{ρ^{l}}_{i}}{ρ_{m}} {v^{l}}_{i} (1 - \frac{ρ_{i}}{ρ_{m}}) (1 - 2 α \frac{{ρ^{r}}_{i}}{ρ_{m}})}{L} \frac{L}{L_{i}} \end{matrix} \end{matrix}$ (13)

然后, 进行以下变量简化:

$\tilde{{ρ^{r}}_{i}} = {ρ^{r}}_{i} / ρ_{m}; \tilde{{ρ^{l}}_{i}} = {ρ^{l}}_{i} / ρ_{m}; \tilde{{v^{l}}_{i}} = {v^{l}}_{i} / L;$

$\tilde{{v^{r}}_{i}} = {v^{r}}_{i} / L; \tilde{{q^{r}}_{0}} = \frac{{q^{r}}_{0}}{ρ_{m} L};$

$\tilde{{q^{l}}_{0}} = \frac{{q^{l}}_{0}}{ρ_{m} L}; b_{i} = L / L_{i}; \tilde{ρ_{i}} = \frac{ρ_{i}}{ρ_{m}} 。$

将简化后的变量称之为标准变量。 $\begin{matrix} \tilde{{ρ^{r}}_{i}} \end{matrix}$ 和 $\begin{matrix} \tilde{{ρ^{l}}_{i}} 、 \tilde{{v^{r}}_{i}} \end{matrix}$ 和 $\begin{matrix} \tilde{{v^{l}}_{i}} \end{matrix}$ 以及 $\begin{matrix} \tilde{{q^{r}}_{0}} \end{matrix}$ 和 $\begin{matrix} \tilde{{q^{l}}_{0}} \end{matrix}$ 分别为分通道 $\begin{matrix} i \end{matrix}$ 右向和左向的标准密度、标准速度以及标准行人流入量。

通过以上等价简化, 式(12)可以等价为:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{\tilde{{ρ^{r}}_{i}}} = b_{i} [{\tilde{ρ}}^{r}_{i - 1} {\tilde{v}}^{r}_{i - 1} (1 - {\tilde{ρ}}_{i - 1}) (1 - 2 α {\tilde{ρ}}_{i - 1}^{l}) - \\ {\tilde{ρ}}^{r}_{i} {\tilde{v}}^{r}_{i} (1 - {\tilde{ρ}}_{i}) (1 - 2 α {\tilde{ρ}}^{l}_{i})] \\ \overset{\cdot}{\tilde{{ρ^{l}}_{i}}} = b_{i} [{\tilde{ρ}}^{l}_{i + 1} {\tilde{v}}^{l}_{i + 1} (1 - {\tilde{ρ}}_{i + 1}) (1 - 2 α {\tilde{ρ}}^{r}_{i + 1}) - \\ {\tilde{ρ}}^{l}_{i} {\tilde{v}}^{l}_{i} (1 - \tilde{ρ_{i}}) (1 - 2 α \tilde{{ρ^{r}}_{i}})] \end{matrix} \end{matrix}$ (14)

具体到每个分通道, 对向行人流的状态空间方程可以表示为:

$\{\begin{matrix} \overset{\cdot}{\tilde{{ρ^{r}}_{1}}} = b_{1} [\tilde{{q^{r}}_{0}} - \tilde{{ρ^{r}}_{1}} \tilde{{v^{r}}_{1}} (1 - \tilde{ρ_{1}}) (1 - 2 α \tilde{{ρ^{l}}_{1}})] \\ \overset{\cdot}{\tilde{{ρ^{r}}_{i}}} = b_{i} [{\tilde{ρ}}^{r}_{i - 1} {\tilde{v}}^{r}_{i - 1} (1 - {\tilde{ρ}}_{i - 1}) (1 - 2 α {\tilde{ρ}}^{l}_{i - 1}) - \\ \tilde{{ρ^{r}}_{i}} \tilde{{v^{r}}_{i}} (1 - \tilde{ρ_{i}}) (1 - 2 α \tilde{{ρ^{l}}_{i}})] \end{matrix}$ (15)

$\{\begin{matrix} \overset{\cdot}{\tilde{{ρ^{l}}_{n}}} = b_{n} [\tilde{{q^{l}}_{0}} - \tilde{{ρ^{l}}_{n}} \tilde{{v^{l}}_{n}} (1 - \tilde{ρ_{n}}) (1 - 2 α \tilde{{ρ^{r}}_{n}})] \\ \overset{\cdot}{\tilde{{ρ^{l}}_{i}}} = b_{i} [{\tilde{ρ}}^{l}_{i + 1} {\tilde{v}}^{l}_{i + 1} (1 - {\tilde{ρ}}_{i + 1}) (1 - 2 α {\tilde{ρ}}^{r}_{i + 1}) - \\ \tilde{{ρ^{l}}_{i}} \tilde{{v^{l}}_{i}} (1 - \tilde{ρ_{i}}) (1 - 2 α \tilde{{ρ^{r}}_{i}})] \end{matrix}$ (16)

对于无控制对向行人流, 本文作如下假设:

(1)通道行人总是期望以最大速度移动, 此时: $\begin{matrix} \tilde{{v^{l}}_{i}} = \tilde{{v^{r}}_{i}} = \tilde{v_{m}^{f}} = v_{m}^{f} / L \end{matrix}$

(2)当行人密度 $\begin{matrix} ρ_{i} = ρ_{m} \end{matrix}$ 时, 标准化密度取最大值 $\begin{matrix} \tilde{ρ_{i}} = \tilde{{ρ^{r}}_{i}} + \tilde{{ρ^{l}}_{i}} = 1, \end{matrix}$ 行人速度 $\begin{matrix} {v^{l}}_{i} = {v^{r}}_{i} = 0, \end{matrix}$ 由于分通道 $\begin{matrix} i \end{matrix}$ 达到最大密度, 行人不能进入分通道 $\begin{matrix} i \end{matrix}$ , 即 $\begin{matrix} {v^{l}}_{i + 1} = {v^{r}}_{i - 1} = 0 。 \end{matrix}$ 由上可知:标准速度 $\begin{matrix} \tilde{{v^{l}}_{i}} = \tilde{{v^{r}}_{i}} = 0 \end{matrix}$ 且 $\begin{matrix} {\tilde{v}}^{l}_{i + 1} = {\tilde{v}}^{r}_{i - 1} = 0 。 \end{matrix}$

(3)无控制条件下, 通道两端行人移动需求足够大, 并总是以最大允许流入量 $\begin{matrix} {q^{l}}_{0} (t) = q_{m}^{l}, {q^{r}}_{0} (t) = q_{m}^{r} \end{matrix}$ 进入通道。根据式(7)可知左向和右向标准行人流入量分别为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} \tilde{{q^{l}}_{0}} = \frac{q_{m}^{l}}{ρ_{m} L} = \tilde{v_{m}^{f}} {(1 - \tilde{{ρ^{r}}_{n}})}^{2} (1 - 2 α \tilde{{ρ^{r}}_{n}} \frac{)}{4} \\ \tilde{{q^{r}}_{0}} = \frac{q_{m}^{r}}{ρ_{m} L} = \tilde{v_{m}^{f}} {(1 - \tilde{{ρ^{l}}_{1}})}^{2} (1 - 2 α \tilde{{ρ^{l}}_{1}} \frac{)}{4} \end{matrix} \end{matrix} \end{matrix}$ (17)

(4)通道行人输出流量不受相邻通道或者出口的限制。

在上述4个假设条件下, 式(15)(16)则表示了无控制下通道内对向行人流动力系统演化的状态空间方程。

2 对向行人流控制模型

2.1 控制目标

管理者期望通道发挥最大能力, 也就是使得通道行人输出流量最大。根据行人流量与密度的关系, 行人流状态目标集可以采用行人密度表示。两个方向行人流比例差距越大, 通道行人流量也越大, 当只允许单向行人移动时, 通道行人流量最大^[40]。但是从行人角度分析, 这种偏向控制并不能同时满足两个方向行人的移动需求, 而且会造成单方向大量行人的拥挤排队, 也会造成一个方向行人速度高于另一方向行人速度的不公平现象。在实际的对向行人流控制中, 既要达到管理者的控制目的即通道流量最大, 又要满足行人需求即行走空间的用户平衡分配。根据无控制下的行人移动条件(3), 假设通道两端的行人需求量相等且均超过最大允许流入量, 并且所有行人接受并服从控制。根据用户平衡条件, 右向和左向行人密度的控制目标应相等^[41], 相对于偏向控制, 这种控制称为均衡控制。根据上述均衡控制的含义, 求得使通道流量最大的标准临界密度为:

$\begin{matrix} \tilde{ρ^{tl}} = \tilde{ρ^{tr}} = \{\begin{matrix} \frac{1 + α - \sqrt[]{α^{2} - α + 1}}{6 α}, 0 < α \leq 1 \\ 0.25, α = 0 \end{matrix} (18) \end{matrix}$

为使得左向和右向行人标准密度 $\begin{matrix} \tilde{{ρ^{l}}_{i}} \end{matrix}$ 和 $\begin{matrix} \tilde{{ρ^{r}}_{i}} \end{matrix}$ 分别指数收敛于临界密度 $\begin{matrix} \tilde{ρ^{tl}}, \tilde{ρ^{tr}}, \end{matrix}$ 可以令:

$\begin{matrix} \{\begin{matrix} \tilde{{ρ^{r}}_{i}} = e^{- {k^{r}}_{i} t + {C^{r}}_{i}} + \tilde{ρ^{tr}} \\ \tilde{{ρ^{l}}_{i}} = e^{- {k^{l}}_{i} t + {C^{l}}_{i}} + \tilde{ρ^{tl}} \end{matrix} (19) \end{matrix}$

式中: $\begin{matrix} {k^{r}}_{i} \end{matrix}$ 和 $\begin{matrix} {k^{l}}_{i} \end{matrix}$ 为控制增益, 且 $\begin{matrix} {k^{r}}_{i} > 0, {k^{l}}_{i} > 0; {C^{r}}_{i} 、 {C^{l}}_{i} \end{matrix}$ 为常数。

根据式(19)可得行人密度关于时间 $\begin{matrix} t \end{matrix}$ 的导数为:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{\tilde{{ρ^{r}}_{i}}} = - {k^{r}}_{i} (\tilde{{ρ^{r}}_{i}} - \tilde{ρ^{tr}}) \\ \overset{\cdot}{\tilde{{ρ^{l}}_{i}}} = - {k^{l}}_{i} (\tilde{{ρ^{l}}_{i}} - \tilde{ρ^{tl}}) \end{matrix} (20) \end{matrix}$

联立式(15)(16)(20)可得:

$\begin{matrix} \{\begin{matrix} b_{1} [\tilde{{q^{r}}_{0}} - \tilde{{ρ^{r}}_{1}} \tilde{{v^{r}}_{1}} (1 - \tilde{ρ_{1}}) (1 - 2 α \tilde{{ρ^{l}}_{1}})] = \\ - {k^{r}}_{1} (\tilde{{ρ^{r}}_{1}} - \tilde{ρ^{tr}}) \\ b_{i} [{\tilde{ρ}}^{r}_{i - 1} {\tilde{v}}^{r}_{i - 1} (1 - {\tilde{ρ}}_{i - 1}) (1 - 2 α {\tilde{ρ}}^{l}_{i - 1}) - \tilde{{ρ^{r}}_{i}} \tilde{{v^{r}}_{i}} (1 - \\ \tilde{ρ_{i}}) (1 - 2 α \tilde{{ρ^{l}}_{i}})] = - {k^{r}}_{i} (\tilde{ρ_{i}^{r}} - \tilde{ρ^{tr}}) \\ b_{n} [\tilde{{q^{l}}_{0}} - \tilde{{ρ^{l}}_{n}} \tilde{{v^{l}}_{n}} (1 - \tilde{ρ_{n}}) (1 - 2 α \tilde{{ρ^{r}}_{n}})] = \\ - {k^{l}}_{n} (\tilde{{ρ^{l}}_{n}} - \tilde{ρ^{tl}}) \\ b_{i} [{\tilde{ρ}}^{l}_{i + 1} {\tilde{v}}^{l}_{i + 1} (1 - {\tilde{ρ}}_{i + 1}) (1 - 2 α {\tilde{ρ}}^{r}_{i + 1}) - \tilde{{ρ^{l}}_{i}} \tilde{{v^{l}}_{i}} (1 - \\ \tilde{ρ_{i}}) (1 - 2 α \tilde{{ρ^{r}}_{i}})] = - {k^{l}}_{i} (\tilde{ρ_{i}^{l}} - \tilde{ρ^{tl}}) \end{matrix} \end{matrix}$ (21)

2.2 控制变量

管理者对行人流的控制主要有两种措施:①限流措施; ②控制行人速度。一般通过设置障碍限制行人流入量或者通过广播提示行人调整走行速度。这两种措施在地铁站、旅游景点等大量人群聚集的地方较为常见。因此, 本文模型的控制变量为左向标准行人流入量 $\begin{matrix} \tilde{{q^{l}}_{0}} \end{matrix}$ 和右向标准行人流入量 $\begin{matrix} \tilde{{q^{r}}_{0}} \end{matrix}$ 以及分通道的行人标准速度 $\begin{matrix} \tilde{{v^{l}}_{i}} \end{matrix}$ 和 $\begin{matrix} \tilde{{v^{r}}_{i}} 。 \end{matrix}$ 控制域为以上控制变量的变化范围, 一方面, 行人的速度不能大于最大速度 $\begin{matrix} v_{m}^{f}, \end{matrix}$ 也不能小于0, 则:

$\begin{matrix} \{\begin{matrix} 0 \leq \tilde{{v^{l}}_{i}} \leq \tilde{v_{m}^{f}} = v_{m}^{f} / L \\ 0 \leq \tilde{{v^{r}}_{i}} \leq \tilde{v_{m}^{f}} = v_{m}^{f} / L \end{matrix} (22) \end{matrix}$

另一方面, 行人流入量不能大于当前最大允许流入量, 也不能小于0。根据式(7)可知:

$\begin{matrix} \{\begin{matrix} 0 \leq \tilde{{q^{l}}_{0}} \leq \tilde{v_{m}^{f}} {(1 - \tilde{{ρ^{r}}_{n}})}^{2} (1 - 2 α \tilde{{ρ^{r}}_{n}} \frac{)}{4} \\ 0 \leq \tilde{{q^{r}}_{0}} \leq \tilde{v_{m}^{f}} {(1 - \tilde{{ρ^{l}}_{1}})}^{2} (1 - 2 α \tilde{{ρ^{l}}_{1}} \frac{)}{4} \end{matrix} (23) \end{matrix}$

2.3 控制模型建立

在均衡控制下, 双向通道的性能指标为通道总行人流量。在行人密度向临界密度收敛过程中, 要求通道总行人瞬时流入量最大。采用标准行人流入量表示, 即:

$\begin{matrix} \max \tilde{q} = \tilde{{q^{r}}_{0}} + \tilde{{q^{l}}_{0}} (24) \end{matrix}$

定理1 通道的流入量最大化等同于通道的行人流出量最大化。

证明行人总标准流出量 $\begin{matrix} \tilde{O} \end{matrix}$ 为左向和右向行人标准流出量的和, 即:

$\begin{matrix} \begin{matrix} \tilde{O} = \tilde{{ρ^{r}}_{n}} \tilde{{v^{r}}_{n}} (1 - \tilde{ρ_{n}}) (1 - 2 α \tilde{{ρ^{l}}_{n}}) + \\ \tilde{{ρ^{l}}_{1}} \tilde{{v^{l}}_{1}} (1 - \tilde{ρ_{1}}) (1 - 2 α \tilde{{ρ^{r}}_{1}}) (25) \end{matrix} \end{matrix}$

将分通道的对向行人流状态方程(21)累计相加, 可以得出:

$\begin{matrix} \tilde{O} = \tilde{q} + \overset{n}{\sum_{i = 1}} - \frac{{k^{r}}_{i}}{b_{i}} (\tilde{{ρ^{r}}_{i}} - \tilde{ρ^{tr}}) + \overset{n}{\sum_{i = 1}} - \frac{{k^{l}}_{i}}{b_{i}} (\tilde{{ρ^{l}}_{i}} - \tilde{ρ^{tr}}) (26) \end{matrix}$

令C= $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ - $\begin{matrix} {k^{r}}_{i} \end{matrix}$ ( $\begin{matrix} \tilde{{ρ^{r}}_{i}} \end{matrix}$ - $\begin{matrix} \tilde{ρ^{tr}} \end{matrix}$ )/b_i+ $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ - $\begin{matrix} {k^{l}}_{i} \end{matrix}$ ( $\begin{matrix} \tilde{{ρ^{l}}_{i}} \end{matrix}$ - $\begin{matrix} \tilde{ρ^{tr}} \end{matrix}$ )/b_i, C为不依赖于控制变量 $\begin{matrix} \tilde{{q^{l}}_{0}} 、 \tilde{{q^{r}}_{0}} 、 \tilde{{v^{l}}_{i}} 、 \tilde{{v^{r}}_{i}} \end{matrix}$ 的常数, 所以, 最大化行人标准流入量 $\begin{matrix} \tilde{q} \end{matrix}$ 等同于最大化行人标准流出量 $\begin{matrix} \tilde{O}, \end{matrix}$ 证毕。

因此, 以通道行人流入量最大化为目标是合理的。综上, 采用标准行人流入量, 可以建立以下线性规划模型:

$\begin{matrix} \{\begin{matrix} \max \tilde{q} = \tilde{{q^{r}}_{0}} + \tilde{q_{0}^{l}} \\ s . t . 式 (21) (22) (23) \end{matrix} (27) \end{matrix}$

在控制过程中, 需要在每个时刻求出线性规划(27)的最优解, 此最优解为控制过程中在时间 $\begin{matrix} t \end{matrix}$ 的输入:瞬时标准流入量 $\begin{matrix} \tilde{{q^{r}}_{0}} 和 \tilde{{q^{l}}_{0}} \end{matrix}$ 以及标准速度 $\begin{matrix} \tilde{{v^{r}}_{i}} 和 \tilde{{v^{l}}_{i}} 。 \end{matrix}$ 上述模型称为均衡反馈控制模型。 $\begin{matrix} {k^{r}}_{i} 、 {k^{l}}_{i} \end{matrix}$ 的取值过大可能会使得线性规划模型(27)无法求出满足约束公式(22)(23)的可行解。在取值过大时, 可以求出满足式(21)的非可行解 $\begin{matrix} \tilde{{q^{r}}_{0}} 和 \tilde{{q^{l}}_{0}} \end{matrix}$ 以及 $\begin{matrix} \tilde{{v^{r}}_{i}} 和 \tilde{{v^{l}}_{i}}, \end{matrix}$ 可以找到一个参数 $\begin{matrix} ω > 0, \end{matrix}$ 使得 $\begin{matrix} \tilde{{q^{r}}_{0}} / ω 、 \tilde{{q^{l}}_{0}} / ω \end{matrix}$ 以及 $\begin{matrix} \tilde{{v^{r}}_{i}} / ω 、 \tilde{{v^{l}}_{i}} / ω \end{matrix}$ 满足约束公式(22)(23)。根据模型(27)的线性特点, $\begin{matrix} {k^{r}}_{i} 、 {k^{l}}_{i} \end{matrix}$ 相应调整为 $\begin{matrix} {k^{r}}_{i} / ω 和 {k^{l}}_{i} / ω \end{matrix}$ 即可满足所有约束条件。

3 数值仿真分析

3.1 模型参数

假设存在一个L=50 m的双向行人通道, 将通道分为5个同等长度的分通道, 每个通道长度为 $\begin{matrix} L_{i} = 10 m, i = 1, 2, \dots, 5, 那么 b_{i} = 5, i = 1, 2, \dots, 5 。 \end{matrix}$ 每个分通道初始行人密度设置为: $\begin{matrix} {ρ^{r}}_{1} = {ρ^{l}}_{1} = 0.34; {ρ^{r}}_{2} = {ρ^{l}}_{2} = 0.29; {ρ^{r}}_{3} = {ρ^{l}}_{3} = 0.13; {ρ^{r}}_{4} = {ρ^{l}}_{4} = 0.4; {ρ^{r}}_{5} = {ρ^{l}}_{5} = 0.014 。 \end{matrix}$ 假设对向行人流冲突强度α =0.5。行人最大速度 $\begin{matrix} v_{m}^{f} \end{matrix}$ =1.5 m/s, 那么0≤ $\begin{matrix} \tilde{v_{i}^{l}} \end{matrix}$ ≤ 0.03, 0≤ $\begin{matrix} \tilde{v_{i}^{r}} \end{matrix}$ ≤ 0.03。令 $\begin{matrix} {k^{l}}_{i} = {k^{r}}_{i} = 0.007, \end{matrix}$ 线性规划(27)存在可行解。

模型运行平台为Windows XP操作系统, CPU2.93 GHz, 采用Matlab软件实现模型, 其中线性规划模型直接使用Matlab自带函数Linprog求解, 模型运行400时间步, 模型运行10次, 其中最少计算时间为3 s, 最多为4.1 s。

3.2 模型结果

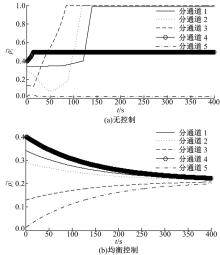
图2~图4为行人密度在无控制和均衡控制下的变化情况。如图4所示, 无控制下所有分通道行人标准密度均增加到1, 产生通道死锁堵塞^[12], 即 $\begin{matrix} \lim_{t \to \infty} ρ_{i} = ρ_{m}, \end{matrix}$ 分通道的死锁堵塞顺序为4-5-3-2-1。如图2和3所示, 分通道1, 2和3全部为右向行人, 而分通道4双向行人各占一半, 分通道5左向行人堵塞居多, 右向行人堵塞较少。在均衡控制策略下, 所有分通道标准行人密度均收敛到0.4226, 即 $\begin{matrix} \lim_{t \to \infty} ρ_{i} = 0.4226 ρ_{m}, \end{matrix}$ 由于左向和右向行人临界密度相等, $\begin{matrix} \lim_{t \to \infty} {ρ^{l}}_{i} = \lim_{t \to \infty} {ρ^{r}}_{i} = 0.2113 ρ_{m} 。 \end{matrix}$ 因此, 均衡控制模型有效避免了对向行人流死锁堵塞。

	Figure Option View Download New Window
	图2 无控制和均衡控制下 $\begin{matrix} \tilde{ρ_{i}^{r}} \end{matrix}$ 比较Fig.2 Comparison of $\begin{matrix} \tilde{ρ_{i}^{r}} \end{matrix}$ in uncontrolled case and equalization control case

	Figure Option View Download New Window
	图3 无控制和均衡控制下 $\begin{matrix} \tilde{ρ_{i}^{l}} \end{matrix}$ 比较Fig.3 Comparison of $\begin{matrix} \tilde{ρ_{i}^{l}} \end{matrix}$ in uncontrolled case and equalization controlled case

	Figure Option View Download New Window
	图4 无控制和均衡控制下 $\begin{matrix} \tilde{ρ_{i}} \end{matrix}$ 比较Fig.4 Comparison of $\begin{matrix} \tilde{ρ_{i}} \end{matrix}$ in uncontrolled case and equalization controlled case

	Figure Option View Download New Window
	图5 无控制和均衡控制下 $\begin{matrix} v_{i}^{r} \end{matrix}$ 比较Fig.5 Comparison of $\begin{matrix} v_{i}^{r} \end{matrix}$ in uncontrolled case and equalization controlled case

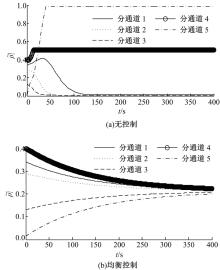
图5和图6分别为左向和右向行人速度在无控制和均衡控制策略下的变化情况。无控制下, 由于通道堵塞, 全部行人均停止移动, 即 $\begin{matrix} \lim_{t \to \infty} {v^{r}}_{i} = 0, \lim_{t \to \infty} {v^{l}}_{i} = 0, i = 1, 2, \dots, 5 。 \end{matrix}$ 其中由于分通道4较早堵塞(见图4), 其右向(见图5)和左向(见图6)行人停止移动, 同时造成分通道3的右向行人和分通道5的左向行人较早停止移动。在均衡控制策略下, 虽然初始时间段内的行人最大速度受到控制约束, 最终行人速度均收敛于最大速度, $\begin{matrix} \lim_{t \to \infty} {v^{r}}_{i} = v_{m}^{f}, \lim_{t \to \infty} {v^{l}}_{i} = v_{m}^{f} 。 \end{matrix}$

	Figure Option View Download New Window
	图6 无控制和均衡控制下左向行人标准速度 $\begin{matrix} \tilde{v_{i}^{l}} \end{matrix}$ 比较Fig.6 Normalized walking speed of leftward pedestrians $\begin{matrix} \tilde{v_{i}^{l}} \end{matrix}$ in uncontrolled case and equalization controlled case

	Figure Option View Download New Window
	图7 无控制和均衡控制下 $\begin{matrix} \tilde{q_{0}^{r}} \end{matrix}$ , $\begin{matrix} \tilde{q_{0}^{l}} \end{matrix}$ , $\begin{matrix} \tilde{q} \end{matrix}$ 比较Fig.7 Comparison of $\begin{matrix} \tilde{q_{0}^{r}} \end{matrix}$ , $\begin{matrix} \tilde{q_{0}^{l}} \end{matrix}$ , $\begin{matrix} \tilde{q} \end{matrix}$ in uncontrolled case and equalization controlled case

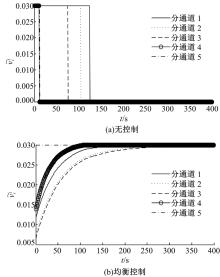
图7为无控制和均衡控制下的流量变化。无控制下, 由于通道堵塞, 右向行人流和左向行人流的标准流入量均收敛于0, 即 $\begin{matrix} \lim_{t \to \infty} \tilde{{q^{r}}_{0}} = 0, \lim_{t \to \infty} \tilde{{q^{l}}_{0}} = 0 \end{matrix}$ , 其中左向行人流量较早收敛于0; 在均衡控制策略下, 行人标准流量呈现上升趋势, 并最终稳定, 其中 $\begin{matrix} \lim_{t \to \infty} \tilde{{q^{r}}_{0}} = 0.00285, \lim_{t \to \infty} \tilde{{q^{l}}_{0}} = 0.00285, \end{matrix}$ 总流量 $\begin{matrix} \lim_{t \to \infty} \tilde{q} = 0.0057 。 \end{matrix}$ 控制结果说明均衡控制策略有效提高了通道行人流量。

上述为半干扰情形下的对向行人流控制策略数值仿真结果, 说明本文均衡控制模型可以有效避免通道行人拥堵, 提高行人走行速度, 在满足行人需求的同时提高了通道通过能力和服务水平。

4 结束语

基于社会力微观模型建立了对向行人流干扰因素下的行人流基本图模型, 首次采用状态空间方程形式描述了双向通道对向行人流演变的系统动力学过程, 能够再现通道对向行人流死锁堵塞现象。基于用户均衡理论和系统最优原则, 提出对向行人流均衡控制目标, 率先提出了面向行人流智能控制的对向行人流均衡反馈控制模型。通过数值分析证明该模型所得控制策略可有效避免行人拥堵, 提高了通道的服务能力。此外, 本文模型的求解计算速度较快, 可满足行人流控制实时性要求。模型的实现依赖于通道行人密度的准确实时获取, 将本文模型与视频监控, 无线传输以及图像识别等智能技术相结合, 可实现行人流的智能控制, 从而提高步行通道的管理水平和效率。

本文模型适用的前提条件是行人速度和密度存在如式(5)所示的比例关系, 很多行人流基本图可以满足模型前提条件, 而且该模型也适用于道路交通实时控制和管理。因此, 模型在行人流和道路交通控制方面具有一定的普适性。本文模型的控制对象为单通道的对向行人流, 并且假设行人的流出量不受其他相邻通道的限制, 模型的不确定性来源于行人是否能够依照控制命令行走。在未来研究中, 需要研究不确定条件下网络中行人流的系统动力学模型, 建立具体控制措施如语音广播, 物理导向和现场指挥等与行人流控制目标的联系, 对现实世界中行人流进行最优控制, 为行人流的智能管理和控制提供理论和技术支持。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	谢征宇, 贾利民, 秦勇, 等. 铁路客运枢纽视频监控采集点布设模型[J]. 中南大学学报: 自然科学版, 2013, 44(增刊2): 254-257. Xie Zheng-yu, Jia Li-min, Qin Yong, et al. Monitor point layout model of video surveillance in railway passenger transport hub[J]. Journal of Central South University (Science and Technology), 2013, 44(Sup. 2): 254-257. [本文引用:1]
[2]	Zhang J, Klingsch W, Schadschneider A, et al. Ordering in bidirectional pedestrian flows and its influence on the fundamental diagram[J]. Journal of Statistical Mechanics: Theory and Experiment, 2012, 2012(2): 1-13. [本文引用:1]
[3]	Lee J, Kim T, Chung J H, et al. Modeling lane formation in pedestrian counter flow and its effect on capacity[J]. KSCE Journal of Civil Engineering, 2016, 20(3): 1099-1108. [本文引用:1]
[4]	Wei J, Zhang H, Guo Y, et al. Experiment of bi-direction pedestrian flow with three-dimensional cellular automata[J]. Physics Letters A, 2015, 379(16): 1081-1086. [本文引用:1]
[5]	Ge Hong-xia, Cheng Rong-jun, Lo Siu-ming. A lattice model for bidirectional pedestrian flow on gradient road[J]. Communications in Theoretical Physics, 2014, 62(2): 259-264. [本文引用:1]
[6]	Hu J, Li Z, Zhang H, et al. Experiment and simulation of the bidirectional pedestrian flow model with overtaking and herding behavior[J]. International Journal of Modern Physics C, 2015, 26(11): 1550131. [本文引用:1]
[7]	Zhang P, Jian X X, Wong S C, et al. Potential field cellular automata model for pedestrian flow[J]. Physical Review E, 2012, 85(2): 021119. [本文引用:1]
[8]	Chen Y Y, Chen N, Wang Y, et al. Modeling pedestrian behaviors under attracting incidents using cellular automata[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 432: 287-300. [本文引用:1]
[9]	Tajima Y, Takimoto K, Nagatani T. Scaling of pedestrian channel flow with a bottleneck[J]. Physica A: Statistical Mechanics and Its Applications, 2001, 294(1): 257-268. [本文引用:1]
[10]	Nowak S, Schadschneider A. A Cellular Automaton Approach for Lane Formation in Pedestrian Counterflow[M]. Berlin Heidelberg: Springer, 2013: 149-160. [本文引用:1]
[11]	李明华, 袁振洲, 许琰, 等. 基于改进格子气模型的对向行人流分层现象的随机性研究[J]. 物理学报, 2015, 64(1): 435-446. Li Ming-hua, Yuan Zhen-zhou, Xu Yan, et al. Rand omness analysis of lane formation in pedestrian counter flow based on improved lattice gas model[J]. Acta Physica Sinica, 2015, 64(1): 435-446. [本文引用:1]
[12]	Feliciani C, Nishinari K. Phenomenological description of deadlock formation in pedestrian bidirectional flow based on empirical observation[J]. Journal of Statistical Mechanics: Theory and Experiment, 2015, 2015(10): 10003. [本文引用:2]
[13]	Wang X, Zheng X, Cheng Y. Evacuation assistants: an extended model for determining effective locations and optimal numbers[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391(6): 2245-2260. [本文引用:1]
[14]	Takimoto K, Tajima Y, Nagatani T. Effect of partition line on jamming transition in pedestrian counter flow[J]. Physica A: Statistical Mechanics and Its Applications, 2002, 308(1): 460-470. [本文引用:1]
[15]	Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic[J]. Nature, 2000, 407(6803): 487-490. [本文引用:1]
[16]	Yang Xiao-xia, Dong Hai-rong, Yao Xiu-ming. Dynamic feature analysis in bidirectional pedestrian flows[J]. Chinese Physics B, 2016, 25(2): 028901. [本文引用:1]
[17]	Zhou J, Shi Z K, Liu Z S. A novel lattice hydrodynamic model for bidirectional pedestrian flow with the consideration of pedestrian's memory effect[J]. Nonlinear Dynamics, 2015, 83(4): 1-15. [本文引用:1]
[18]	Zhou J, Shi Z K. A new lattice hydrodynamic model for bidirectional pedestrian flow with the consideration of lateral discomfort[J]. Nonlinear Dynamics, 2015, 81(3): 1113-1131. [本文引用:1]
[19]	Zhou J, Shi Z K. A new lattice hydrodynamic model for bidirectional pedestrian flow with the consideration of pedestrian's anticipation effect[J]. Nonlinear Dynamics, 2015, 81(3): 1247-1262. [本文引用:1]
[20]	Zhou J, Shi Z K. Lattice hydrodynamic model for bidirectional pedestrian flow with the consideration of pedestrian density difference[J]. International Journal of Modern Physics C, 2015, 26(8): 1550092. [本文引用:1]
[21]	Chalons C. Numerical approximation of a macroscopic model of pedestrian flows[J]. SIAM Journal on Scientific Computing, 2007, 29(2): 539-555. [本文引用:1]
[22]	Hoogendoorn S P, van Wageningen-Kessels F, Daamen W, et al. Continuum theory for pedestrian traffic flow: local route choice modelling and its implications[J]. Transportation Research Part C: Emerging Technologies, 2015, 59: 183-197. [本文引用:1]
[23]	Hughes R L. A continuum theory for the flow of pedestrians[J]. Transportation Research Part B: Methodological, 2002, 36(6): 507-535. [本文引用:1]
[24]	Shende A, Kachroo P, Reddy K C, et al. Optimal control of pedestrian evacuation in a corridor[C]//IEEE Conference on Intelligent Transportation Systems, Seattle, WA, USA, 2007: 385-390. [本文引用:1]
[25]	李曼, 王艳辉, 贾利民. 城市轨道交通车站客流模态与控制策略[J]. 东南大学学报: 自然科学版, 2015, 45(6): 1203-1208. Li Man, Wang Yan-hui, Jia Li-min. Passenger flow modes and control strategies in urban rail transit station[J]. Journal of Southeast University (Natural Science Edition), 2015, 45(6): 1203-1208. [本文引用:1]
[26]	Shende A, Singh M P, Kachroo P. Optimization-based feedback control for pedestrian evacuation from an exit corridor[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1167-1176. [本文引用:1]
[27]	Haddad J, Ramezani M, Geroliminis N. Cooperative traffic control of a mixed network with two urban regions and a freeway[J]. Transportation Research Part B: Methodological, 2013, 54: 17-36. [本文引用:1]
[28]	Teodorovic D, Vukadinovic K. Traffic Control and Transport Planning: a Fuzzy Sets and Neural Networks Approach[M]. New York: Springer, 2012. [本文引用:1]
[29]	李志斌, 金茂菁, 刘攀, 等. 提高高速公路通行效率的可变限速控制策略[J]. 吉林大学学报: 工学版, 2013, 43(5): 1204-1209. Li Zhi-bin, Jin Mao-jing, Liu Pan, et al. Evaluation of impact variable speed limits on improving traffic efficiency on freeways[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1204-1209. [本文引用:1]
[30]	Zohdy I H, Rakha H. Game theory algorithm for intersection-based cooperative adaptive cruise control (CACC) systems[C]//15th International IEEE Conference on Intelligent Transportation Systems, Anchorage, Alaska, USA, 2012: 1097-1102. [本文引用:1]
[31]	Hafner M R, Cunningham D, Caminiti L, et al. Cooperative collision avoidance at intersections: Algorithms and experiments[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3): 1162-1175. [本文引用:1]
[32]	姚荣涵, 张晓彤, 廉莲. 交叉口可变导向车道控制优化模型[J]. 吉林大学学报: 工学版, 2017, 47(4): 1048-1054. Yao Rong-han, Zhang Xiao-tong, Lian Lian. Optimization model for controlling reversible approach lanes at signalized intersections[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(4): 1048-1054. [本文引用:1]
[33]	贾洪飞, 李永行, 杨丽丽. 基于交通状态估计的快速路交通联合控制[J]. 吉林大学学报: 工学版, 2017, 47(1): 76-81. Jia Hong-fei, Li Yong-xing, Yang Li-li. Expressway traffic joint control based on traffic state estimation[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 76-81. [本文引用:1]
[34]	Kachroo P, Al-Nasur S J, Wadoo S A, et al. Pedestrian Dynamics: Feedback Control of Crowd Evacuation[M]. New York: Springer, 2008. [本文引用:1]
[35]	Shende A, Singh M P, Kachroo P. Optimal feedback flow rates for pedestrian evacuation in a network of corridors[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3): 1053-1066. [本文引用:1]
[36]	Wadoo S A, Kachroo P. Feedback control of crowd evacuation in one dimension[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(1): 182-193. [本文引用:1]
[37]	曾广湘, 薛郁. 准滑模控制应用于行人通道的交通瓶颈[J]. 物理学报, 2011, 60(1): 014502. Zeng Guang-xiang, Xue Yu. Application of the quasi-sliding-mode control to traffic bottleneck in pedestrian channel[J]. Acta Physica Sinica, 2011, 60(1): 014502. [本文引用:1]
[38]	Nikolić M, Bierlaire M, Farooq B, et al. Probabilistic speed-density relationship for pedestrian traffic[J]. Transportation Research Part B: Methodological, 2016, 89: 58-81. [本文引用:1]
[39]	Greenshields B D, Bibbins J R, Channing W S, et al. A study of traffic capacity[J]. Highway Research Board Proceedings, 1935, 14: 448-477. [本文引用:1]
[40]	Wong S C, Leung W L, Chan S H, et al. Bidirectional pedestrian stream model with oblique intersecting angle[J]. Journal of Transportation Engineering, 2010, 136(3): 234-242. [本文引用:1]
[41]	Gawron C. An iterative algorithm to determine the dynamic user equilibrium in a traffic simulation model[J]. International Journal of Modern Physics C, 1998, 9(3): 393-407. [本文引用:1]

2013

0.0

. 2013, 44(增刊2):254-257

Monitor point layout model of video surveillance in railway passenger transport hub

铁路客运枢纽视频监控采集点布设模型

Xie Zheng-yu , Jia Li-min , Qin Yong

谢征宇, 贾利民, 秦勇

针对铁路客运枢纽视频监控采集点布设问题,给出视频监控采集点布设的流程,建立采集点布设模型,并设计启发式算法对模型进行求解。选取某铁路客运枢纽为例对模型和算法进行验证,采集点布设结果可实现枢纽内功能区域的全覆盖,保证枢纽内功能区域图像采集信息的完整性、连续性和有效性。

... 0 引言目前,大型行人集散设施(如地铁站,机场,大型商场等)正向着信息化、智能化方向发展,通过在一些重点区域和位置装设摄像头、传感器等感知设备监测行人流动^[1],并通过无线网络传输设备,管理人员可以获得某一区域行人流的基本信息(如速度、密度和流量等),这为行人流的智能控制提供了数据来源和技术支持 ...

2012

0.0

... 对向行人流是指在一条双向通道内同时存在两个向相反方向行走的行人流现象,相比于单向行人流,由于不同方向的行人流之间存在强烈正面冲突和交叉冲突^[2],对向行人流中行人之间的相互影响更甚,堵塞的概率也会更高 ...

2016

0.0

... 社会力模型^[3]、元胞自动机模型^[4]、格子气模型^[5]等在内的微观仿真模型将行人看作离散的个体,通过模拟个体行为体现群体动力学特征,这些微观模型凭借模型简单、容易编程等优点,成为研究对向行人流的一类重要模型 ...

2015

0.0

2014

0.0

2015

0.0

... 微观模型在模拟行人流各种现象(如行人超越^[6]、冲突和吸引^[7,8]、行人偏走^[9]、随机分层^[10,11]和对向行人冲突所致的死锁堵塞现象^[12]等)方面具有一定优势 ...

2012

0.0

2015

0.0

2001

0.0

2013

0.0

2015

0.0

. 2015, 64(1):435-446 DOI:doi:10.7498/aps.64.018903

Randomness analysis of lane formation in pedestrian counter flow based on improved lattice gas model

基于改进格子气模型的对向行人流分层现象的随机性研究

Li Ming-hua , Yuan Zhen-zhou , Xu Yan

李明华, 袁振洲, 许琰

摘　要：在考虑行人视野范围的随机偏走格子气模型基础上，引入行人对前方开阔区域的移动偏好特性，提出改进的格子气模型，对通道内对向行人流进行仿真研究。模型再现了对向行人流在不同密度下出现的3种演化过程，发现了行人密度与对向行人流分层现象的形成具有随机性，以及统计了概率的变化趋势，同时分析了分层现象形成概率与系统几何尺寸参数、移动强度参数、右行人流比例参数和视野范围参数等的关系。分析结果表明，改进的模型能够再现实际低密度下对向行人流不会出现分层现象的特性。根据分层形成的概率，可将对向行人流的密度分为5个区间，不同区间的行人流演化过程各有差异。模型和分析结果对理解对向行人流的动态演化过程，提高通道内对向行人流的走行效率有一定帮助。

2015

0.0

... 如图4所示,无控制下所有分通道行人标准密度均增加到1,产生通道死锁堵塞^[12],即 limt→∞ρi=ρm,分通道的死锁堵塞顺序为4-5-3-2-1 ...

2012

0.0

2002

0.0

2000

0.0

... 假设 Fp=Spvmfρp/ρm,ρm为堵塞密度,Sp为行人 p与其他行人之间的拥挤作用强度^[15],令 Sp=1/τ,当行人匀速运动时,令 ap=0,得: ...

2016

0.0

2015

0.0

2015

0.0

2015

0.0

2015

0.0

2007

0.0

... 宏观模型将行人群体视作连续流体,通常采用偏微分方程描述行人群体的移动行为,此类模型包括一维^[21]和二维流体力学(LWR)模型^[22,23],相对于微观模型,宏观模型的行人群体模拟时间较少^[24],非常适于大规模行人群体的系统动力学建模和实时控制^[25,26] ...

2015

0.0

2002

0.0

2007

0.0

2015

0.0

. 2015, 45(6):1203-1208

Passenger flow modes and control strategies in urban rail transit station

城市轨道交通车站客流模态与控制策略

Li Man , Wang Yan-hui , Jia Li-min.

李曼, 王艳辉, 贾利民

2011

0.0

2013

0.0

... 目前,基于宏观模型的车流控制研究较多^{[27,28,29,30,31,32,33]},行人流控制研究主要集中在疏散过程中的单向行人流控制^{[34,35,36,37]},而关于冲突更为严重的对向行人流的控制研究较少,这在一定程度上减缓了行人集散设施智能化发展进程 ...

2012

0.0

2013

0.0

. 2013, 43(5):1204-1209 DOI:doi:10.7964/jdxbgxb201305009

Evaluation of impact variable speed limits on improving traffic efficiency on freeways

提高高速公路通行效率的可变限速控制策略

Li Zhi-bin , Jin Mao-jing , Liu Pan

李志斌, 金茂菁, 刘攀

To reduce vehicle delay at recurrent bottlenecks on freeways, this study aims to develop a control strategy of Variable Speed Limits (VSL) to improve the traffic efficiency near bottlenecks. First, the relationship between the capacity drop and traffic efficiency was analyzed. Then a control strategy of VSL that aims to prevent the capacity drop was proposed. The implementation of VSL at several different bottlenecks and the expected effects were discussed. The proposed strategy was evaluated for a merging bottleneck via simulation. The results show that the total travel time was reduced by 25.5% by the VSL, and the total delay was reduced by 56.1%. The traffic efficiency in the vicinity of recurrent bottleneck was improved by this VSL control strategy.

为减少高速公路常发瓶颈区域车辆行驶延误,针对提高瓶颈区域通行效率的可变限速控制策略与控制效果进行了研究。阐述了瓶颈通行能力下降现象与通行效率的关系,提出防止瓶颈区域通行能力下降的可变限速控制策略,讨论了不同瓶颈类型的可变限速控制方法与理论效果。以入口匝道交通瓶颈为例,对可变限速控制策略的效果进行仿真分析,结果表明该策略减少了车辆总通行时间25.5%,减少车辆总行驶延误56.1%,有效提升了高速公路常发瓶颈区域通行效率。

2012

0.0

2013

0.0

2017

0.0

. 2017, 47(4):1048-1054 DOI:doi:10.13229/j.cnki.jdxbgxb201704006

Optimization model for controlling reversible approach lanes at signalized intersections

交叉口可变导向车道控制优化模型

Yao Rong-han , Zhang Xiao-tong , Lian Lian.

姚荣涵, 张晓彤, 廉莲

摘　要：为了均衡交通流向分布且保证控制方案平稳过渡,提出具有可变导向车道的交叉口时空资源优化模型以及可变导向车道标志与信号灯组协调控制方法。为验证本文模型与方法的有效性,借助数学软件MATLAB、交通仿真软件VISSIM及其信号控制逻辑工具VisVAP,使用一个算例对比分析可变导向车道控制方案与固定导向车道控制方案。结果表明：与固定导向车道控制方案相比,可变导向车道控制方案使具有可变导向车道的进口道及交叉口的车均延误分别降低3%-50%和7%-15%,说明可变导向车道控制优化模型能适应交叉口交通需求的潮汐特性,可变导向车道标志与信号灯组协调控制方法能保证交通流安全、平稳运行。

2017

0.0

. 2017, 47(1):76-81

Expressway traffic joint control based on traffic state estimation

基于交通状态估计的快速路交通联合控制

Jia Hong-fei , Li Yong-xing , Yang Li-li.

贾洪飞, 李永行, 杨丽丽

2008

0.0

2013

0.0

2010

0.0

2011

0.0

. 2011, 60(1):014502-

Application of the quasi-sliding-mode control to traffic bottleneck in pedestrian channel

准滑模控制应用于行人通道的交通瓶颈

Zeng Guang-xiang , Xue Yu.

曾广湘, 薛郁

2016

0.0

... Nikoli c'根据社会力模型中加速度的不同表现形式和行人匀速的假设推导出了各种单向行人流基本图^[38],其中Greenshields基本图^[39]推导过程如下 ...

1935

0.0

... Nikoli c'根据社会力模型中加速度的不同表现形式和行人匀速的假设推导出了各种单向行人流基本图^[38],其中Greenshields基本图^[39]推导过程如下 ...

2010

0.0

... 两个方向行人流比例差距越大,通道行人流量也越大,当只允许单向行人移动时,通道行人流量最大^[40] ...

1998

0.0

... 根据用户平衡条件,右向和左向行人密度的控制目标应相等^[41],相对于偏向控制,这种控制称为均衡控制 ...