车辆作用下钢-混凝土组合简支梁动力特性

引用本文

魏志刚, 时成林, 刘寒冰, 张云龙. 车辆作用下钢-混凝土组合简支梁动力特性[J].吉林大学学报（工学版）, 2017,47(6): 1744-1752
WEI Zhi-gang, SHI Cheng-lin, LIU Han-bing, ZHANG Yun-long. Dynamic characteristics of steel-concrete composite simply supported beam under vehicles[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1744-1752 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706010
Permissions

车辆作用下钢-混凝土组合简支梁动力特性

魏志刚^1,², 时成林^1,³, 刘寒冰¹, 张云龙⁴

1.吉林大学交通学院,长春 130022

2.吉林省高等级公路建设局,长春 130033

3.吉林省交通科学研究所科研开发中心,长春 130012

4.吉林建筑大学交通科学与工程学院,长春 130118

通讯作者：张云龙(1975-),男,副教授,博士.研究方向:桥梁检测与加固.E-mail:zhangyunlong@jlju.edu.cn

作者简介:魏志刚(1977-),男,高级工程师,博士研究生.研究方向:桥梁检测与加固.E-mail:wzg770718@163.com

基金:国家自然科学基金面上项目(51478203)

摘要

首先,在考虑组合梁结合面剪切滑移效应的情况下,推导了车辆作用下钢-混组合梁的刚度分布函数。然后,采用待定系数表达组合梁和车辆的振动位移函数。进而基于矩阵传递法的基本思想,根据变形协调及力的平衡条件,建立了以待定系数表达的整个车-组合梁振动系统的振动方程,根据该振动方程可以计算出车辆作用下钢-混凝土简支梁的自振频率和振型。最后,采用有限元方法验证了本文方法的有效性和可靠性。

关键词: 桥梁工程; 动力特性; 钢-混凝土组合梁桥; 剪切滑移

中图分类号:TU311 文献标志码:A 文章编号:1671-5497(2017)06-1744-09

Dynamic characteristics of steel-concrete composite simply supported beam under vehicles

WEI Zhi-gang^1,², SHI Cheng-lin^1,³, LIU Han-bing¹, ZHANG Yun-long⁴

1.College of Transportation,Jilin University,Changchun 130022, China

2.Jilin Provincial High Class Highway Construction Bureau, Changchun 130033, China

3.Scientific Research and Development Center, Jilin Provincial Transport Scientific Research Institute, Changchun 130012, China

4.School of Transportation Science & Engineering, Jilin Jianzhu University, Changchun 130118, China

Abstract

In this paper, first, the stiffness distribution function of steel-concrete composite beam under vehicles is derived, in which the effect of share slip of the composite beam is considered. Then, the undetermined coefficients are used to express the vibration functions of the composite beam and the vehicles. Further, based on the matrix transfer method, the vibration equation of the vehicle-beam vibration system expressed by the undetermined coefficients is established using the deformation compatibility and the force equilibrium condition. The natural frequencies and mode shapes of the steel-concrete simply supported beam under vehicles can be calculated by this vibration equation. Finally, the validity and reliability of the presented method are verified by finite element method.

Keyword: bridge engineering; dynamic characteristics; steel-concrete composite beam; shear slip

Show Figures

0 引言

由于钢-混凝土组合梁具有能够充分发挥钢材的抗拉性能强、混凝土抗压强度高的材料优势, 并且能够自架设施工、建筑垃圾少等优点, 在桥梁工程领域得到了越来越广泛的应用^{[1, 2]}。动力特性对该类桥梁的损伤具有一定的敏感性, 因此基于动力特性的损伤识别和状态评估越来越受到人们的关注, 而测试到的动力特性的准确性是决定桥梁损伤识别和状态评估可靠性的关键因素。

在桥梁的动力特性测试过程中, 为了获得具有较高信噪比的响应信号, 往往采用车辆对桥梁进行激振, 例如采用通行车辆、跳车试验^[3]及跑车试验等。有关研究成果表明, 测试到的车辆作用下的桥梁频率实际上是以桥梁振动为主要振动形式的车桥耦合振动系统的频率, 车辆作用下的桥梁频率与桥梁的自振频率存在一定的差异, 有时这种差异甚至可以掩盖桥梁自身损伤导致的自振频率变化^{[4, 5]}。

自从发现车辆作用会导致桥梁的动力特性发生变化以来, 人们试图通过实验研究和理论分析等手段来剖析该问题的本质。Kim等^[6]通过对Nongro桥的实验监测, 得出了轻车辆作用下的桥梁频率比重车辆作用下的桥梁频率高5.4%的结论。苏木标等^[7]从车-桥耦合振动的基本原理出发, 探讨了车辆对简支梁桥自振频率的影响。de Roeck等^[8]采用有限元方法计算了车辆作用下连续梁桥的自振频率。程永春^[9]、Tan等^[10]形成了车辆作用下完好简支梁桥自振和裂缝简支梁桥自振频率的计算方法, 并提出了剔除车辆对桥梁自振频率影响的方法^[11]。

有关研究资料^{[12, 13]}表明, 钢-混组合梁的抗弯性能不仅取决于钢梁的抗弯刚度和混凝土顶板的抗弯刚度, 钢-混结合面的剪切滑移效应也是影响其抗弯性能的因素。已有的研究成果并没有考虑到车辆荷载的不同会导致桥梁抗弯性能发生变化这一现象, 因此, 这些研究成果并不能直接应用到车辆作用下钢-混组合梁的动力特性分析中。

本文首先推导了车辆作用下考虑结合面剪切滑移效应的钢-混组合梁的刚度分布函数。然后, 从车-桥耦合振动的基本原理出发, 建立了以待定系数表达的车辆作用下组合梁的振动方程, 进而求解得到车辆作用下钢-混组合梁的动力特性。

1 振动方程及位移函数

多辆车作用下的组合梁如图1所示, 其中车辆编号为1, 2, …, p-1, p, p+1, …, s。s辆车把组合梁分成了2s+1个梁段, 每个梁段的编号可以用符号b₁, R₁, …, b_p, R_p, b_p+₁, …, R_s, b_s+₁表示。第p辆车的车体质量为 $\begin{matrix} m_{b}^{p} \end{matrix}$ ; 两个车轮质量为 $\begin{matrix} m_{t 1}^{p} \end{matrix}$ 、 $\begin{matrix} m_{t 2}^{p} \end{matrix}$ ; 车体转动惯量为 $\begin{matrix} I_{b}^{p} \end{matrix}$ ; 车辆的悬架刚度为 $\begin{matrix} k_{t 1}^{p} \end{matrix}$ 、 $\begin{matrix} k_{t 2}^{p} \end{matrix}$ ; 轮胎刚度为 $\begin{matrix} k_{a 1}^{p} \end{matrix}$ 、 $\begin{matrix} k_{a 2}^{p} \end{matrix}$ ; 车轮间距为a^p。

	Figure Option View Download New Window
	图1 多辆车作用下的组合梁Fig.1 Composite beam under action of multiple vehicles

1.1 组合梁振动方程及位移函数

钢-混组合梁自由振动方程为:

m $\begin{matrix} \frac{\partial^{2} y (x, t)}{\partial t^{2}} \end{matrix}$ + $\begin{matrix} \frac{\partial}{\partial x^{2}} \end{matrix} \begin{matrix} [K (x) \frac{\partial^{2} y (x, t)}{\partial x^{2}}] \end{matrix}$ =0 (1)

式中:m为组合梁单位长度质量, 其数值为单位长度的钢梁和混凝土顶板质量之和; y(x, t)为组合梁x截面在t时刻的竖向位移; K(x)为考虑结合面剪切滑移效应和不同车辆荷载作用的组合梁刚度分布函数。

鉴于K(x)的复杂性, 从式(1)中很难得到组合梁振型函数的显式表达。在此, 采用矩阵传递方法的基本思想, 把各梁段又细划为多个子梁段, 只要子梁段的长度足够小, 便可以认为在一个子梁段内组合梁的抗弯刚度是不变的。

b_p+₁梁段中子梁段的划分如图2所示, 该梁段被细分为m个子梁段; 各子梁段的编号分别为1, 2, …, Q-1, Q, Q+1, …, m, 各子梁段的长度分别为 $\begin{matrix} l_{b_{p + 1}}^{1} \end{matrix}$ , $\begin{matrix} l_{b_{p + 1}}^{2} \end{matrix}$ , …, $\begin{matrix} l_{b_{p + 1}}^{Q - 1} \end{matrix}$ , $\begin{matrix} l_{b_{p + 1}}^{Q} \end{matrix}$ , $\begin{matrix} l_{b_{p + 1}}^{Q + 1} \end{matrix}$ , …, $\begin{matrix} l_{b_{p + 1}}^{m} \end{matrix}$ 。

	Figure Option View Download New Window
	图2 b_p+₁梁段划分示意图Fig.2 Sketch for division of section b_p+₁

令 $\begin{matrix} K_{b_{p + 1}}^{Q} \end{matrix}$ 为第Q个子梁段的等效抗弯刚度:

$\begin{matrix} K_{b_{p + 1}}^{Q} = \frac{1}{l_{b_{p + 1}}^{Q}} \int_{_{x_{2}^{p} + \overset{Q - 1}{\sum_{i = 1}} l_{b_{p + 1}}^{i}}}^{x_{2}^{p}} K (x) dx (2) \end{matrix}$

令ξ =x- $\begin{matrix} {x^{p}}_{2} \end{matrix}$ - $\begin{matrix} \overset{Q - 1}{\sum_{i = 1}} \end{matrix} \begin{matrix} l_{b_{p + 1}}^{i} \end{matrix}$ , 对于第Q个子梁段, 有0≤ ξ ≤ $\begin{matrix} l_{b_{p + 1}}^{Q} \end{matrix}$ 。其自由振动方程可以表示为:

$m \frac{\partial^{2} y (ξ, t)}{\partial t^{2}} + K_{b_{p + 1}}^{Q} \frac{\partial^{4} y (ξ, t)}{\partial ξ^{4}} = 0 (3)$

令：

$y (ξ, t) = φ_{b_{p + 1}}^{Q} (ξ) e^{jωt} (4)$

式中: $\begin{matrix} φ_{b_{p + 1}}^{Q} \end{matrix}$ 为b_p+₁梁段第Q个子梁段的振型函数; ω 为车-桥耦合振动系统的角频率。

联立式(3)(4)可得:

$\begin{matrix} \begin{matrix} φ_{b_{p + 1}}^{Q} (ξ) = A_{b_{p + 1}}^{Q} \sin β_{b_{p + 1}}^{Q} ξ + B_{b_{p + 1}}^{Q} \cos β_{b_{p + 1}}^{Q} ξ + \\ C_{b_{p + 1}}^{Q} \sin h β_{b_{p + 1}}^{Q} ξ + D_{b_{p + 1}}^{Q} \cos h β_{b_{p + 1}}^{Q} ξ (5) \end{matrix} \end{matrix}$

式中: $\begin{matrix} A_{b_{p + 1}}^{Q} \end{matrix}$ 、 $\begin{matrix} B_{b_{p + 1}}^{Q} \end{matrix}$ 、 $\begin{matrix} C_{b_{p + 1}}^{Q} \end{matrix}$ 、 $\begin{matrix} D_{b_{p + 1}}^{Q} \end{matrix}$ 为 $\begin{matrix} φ_{b_{p + 1}}^{Q} \end{matrix}$ 的4个待定系数, ( $\begin{matrix} β_{b_{p + 1}}^{Q} \end{matrix}$ )⁴=ω ²m/ $\begin{matrix} K_{b_{p + 1}}^{Q} \end{matrix}$ 。

1.2 车辆振动方程及位移函数

第p辆车的平衡方程为:

$\begin{matrix} \{\begin{matrix} m_{t 1}^{p} y_{t 1}^{p} + k_{a 1}^{p} (y_{t 1}^{p} + y_{1}^{p}) + k_{t 1}^{p} y_{12} = 0 \\ m_{t 2}^{p} y_{t 2}^{p} + k_{a 2}^{p} (y_{t 2}^{p} + y_{2}^{p}) + k_{t 2}^{p} y_{21} = 0 \\ m_{b}^{p} y_{b}^{p} + k_{t 1}^{p} y_{11} + k_{t 2}^{p} y_{22} = 0 \\ I_{b}^{p} θ^{p} - \frac{a^{p}}{2} k_{t 1}^{p} y_{11} + \frac{a^{p}}{2} k_{t 2}^{p} y_{21} = 0 \end{matrix} (6) \end{matrix}$

式中: $\begin{matrix} y_{b}^{p} \end{matrix}$ 为车体质量 $\begin{matrix} m_{b}^{p} \end{matrix}$ 的位移; $\begin{matrix} y_{t 1}^{p} \end{matrix}$ 、 $\begin{matrix} y_{t 2}^{p} \end{matrix}$ 分别为车轮质量的位移; $\begin{matrix} y_{1}^{p} \end{matrix}$ 、 $\begin{matrix} y_{2}^{p} \end{matrix}$ 分别为组合梁在 $\begin{matrix} x_{1}^{p} \end{matrix}$ 和 $\begin{matrix} x_{2}^{p} \end{matrix}$ 处的变形; y₁₁= $\begin{matrix} y_{b}^{p} \end{matrix}$ - $\begin{matrix} y_{t 1}^{p} \end{matrix}$ + $\begin{matrix} s_{1}^{p} \end{matrix}$ a^pθ ^p; y₁₂= $\begin{matrix} y_{b}^{p} \end{matrix}$ - $\begin{matrix} y_{t 1}^{p} \end{matrix}$ - $\begin{matrix} s_{1}^{p} \end{matrix}$ a^pθ ^p; y₂₁= $\begin{matrix} y_{b}^{p} \end{matrix}$ - $\begin{matrix} y_{t 2}^{p} \end{matrix}$ - $\begin{matrix} s_{2}^{p} \end{matrix}$ a^pθ ^p; y₂₂= $\begin{matrix} y_{b}^{p} \end{matrix}$ - $\begin{matrix} y_{t 2}^{p} \end{matrix}$ + $\begin{matrix} s_{2}^{p} \end{matrix}$ a^pθ ^p; θ ^p为车体转角。

由于车辆在平衡位置附近做简谐振动, 则有:

$\begin{matrix} \{\begin{matrix} y_{t 1}^{p} = Y_{t 1}^{p} e^{jωt} \\ y_{t 2}^{p} = Y_{t 2}^{p} e^{jωt} \\ y_{b}^{p} = Y_{b}^{p} e^{jωt} \\ θ^{p} = {\hat{θ}}^{p} e^{jωt} \end{matrix} (7) \end{matrix}$

式中: $\begin{matrix} Y_{t 1}^{p} \end{matrix}$ 、 $\begin{matrix} Y_{t 2}^{p} \end{matrix}$ 、 $\begin{matrix} Y_{b}^{p} \end{matrix}$ 、 $\begin{matrix} {\hat{θ}}^{p} \end{matrix}$ 分别为 $\begin{matrix} y_{t 1}^{p} \end{matrix}$ 、 $\begin{matrix} y_{t 2}^{p} \end{matrix}$ 、 $\begin{matrix} y_{b}^{p} \end{matrix}$ 、θ ^p的振动幅值。

2 组合梁抗弯刚度分布函数

s辆车作用下组合梁受到的竖向力如图3所示。令:

$\begin{matrix} \begin{matrix} F_{1} = \frac{1}{L} [P_{1} (l - x_{1}) + P_{2} (l - x_{2}) + \dots + \\ P_{2 i - 1} (l - x_{2 i - 1}) + P_{2 i} (l - x_{2 i}) + \\ P_{2 i + 1} (l - x_{2 i + 1}) + \dots + \\ P_{2 s - 1} (l - x_{2 s - 1}) + P (l - x_{2 s})] (8) \end{matrix} \end{matrix}$

则可得到组合梁各处的弯矩为:

M_p(x)= $\begin{matrix} \{\begin{matrix} F_{1} x, 0 \leq x < x_{1} \\ F_{1} x - P_{1} (x - x_{1}), x_{1} \leq x < x_{2} \\ F_{1} x - P_{1} (x - x_{1}) - P_{2} (x - x_{2}), \\ x_{2} \leq x < x_{3} \\ ︙ \\ F_{1} x - P_{1} (x - x_{1}) - P_{2} (x - x_{2}) - \dots - \\ P_{2 i - 1} (x - x_{2 i - 1}), x_{2 i - 1} \leq x < x_{2 i} \\ F_{1} x - P_{1} (x - x_{1}) - P_{2} (x - x_{2}) - \dots - \\ P_{2 i} (x - x_{2 i}), x_{2 i} \leq x < x_{2 i + 1} \\ ︙ \\ F_{1} x - P_{1} (x - x_{1}) - P_{2} (x - x_{2}) - \dots - \\ P_{2 i - 1} (x - x_{2 i - 1}) - P_{2 i} (x - x_{2 i}) - \dots - \\ P_{2 s - 1} (x - x_{2 s - 1}), x_{2 s - 1} \leq x < x_{2 s} \\ F_{1} x - P_{1} (x - x_{1}) - P_{2} (x - x_{2}) - \dots - \\ P_{2 i - 1} (x - x_{2 i - 1}) - P_{2 i} (x - x_{2 i}) - \dots - \\ P_{2 s - 1} (x - x_{2 s - 1}) - P_{2 s} (x - x_{2 s}), \\ x_{2 s} \leq x < l \end{matrix} \end{matrix}$ (9)

	Figure Option View Download New Window
	图3 s辆车作用下的简支梁受力模式Fig.3 Force exerting mode of simply supported beam with number of s vehicles

令K₀=E_pI_p+E_bI_b, 其中E_b和E_p分别为钢梁和混凝土顶板的弹性模量; I_b和I_p分别为钢梁和混凝土顶板的截面惯性矩。

在弯矩M_p(x)作用下, 混凝土顶板形心轴处的应变为^[12]:

$\begin{matrix} u'_{b 0} (x) = c_{1} \cos h (Rx) + c_{2} \sin h (Rx) + \frac{z_{d}}{χ K_{0}} M_{p} (x) (10) \end{matrix}$

式中:R= $\begin{matrix} \sqrt[]{x / α} \end{matrix}$ , α =E_bA_b/k, x=1+E_bA_b/(E_pA_p)+E_bA_b $\begin{matrix} z_{d}^{2} \end{matrix}$ /K₀, A_b、A_p分别为钢梁和混凝土顶板的横断面面积; z_d为钢梁和混凝土顶板形心轴之间的竖向距离。

将式(9)代入式(10)可得:

$\begin{matrix} \begin{matrix} u'_{b 0} (x) = \\ \{\begin{matrix} d_{1} \cos h (Rx) + d_{2} \sin h (Rx) + λ_{1} x + λ_{2}, \\ 0 \leq x < x_{1} \\ d_{3} \cos h (Rx) + d_{4} \sin h (Rx) + λ_{3} x + λ_{4}, \\ x_{1} \leq x < x_{2} \\ d_{5} \cos h (Rx) + d_{6} \sin h (Rx) + λ_{5} x + λ_{6}, \\ x_{2} \leq x < x_{3} \\ ︙ \\ d_{2 (2 i - 1) + 1} \cos h (Rx) + d_{2 (2 i - 1) + 2} \sin h (Rx) + \\ λ_{2 (2 i - 1) + 1} x + λ_{2 (2 i - 1) + 2}, x_{2 i - 1} \leq x < x_{2 i} \\ d_{2 \cdot 2 i + 1} \cos h (Rx) + d_{2 \cdot 2 i + 2} \sin h (Rx) + λ_{2 \cdot 2 i + 1} x + \\ λ_{2 \cdot 2 i + 2}, x_{2 i} \leq x < x_{2 i + 1} \\ ︙ \\ d_{2 (2 s - 1) - 1} \cos h (Rx) + d_{2 (2 s - 1)} \sin h (Rx) + λ_{2 (2 s - 1) - 1} x + \\ λ_{2 (2 s - 1)}, x_{2 s - 2} \leq x < x_{2 s - 1} \\ d_{2 \cdot 2 s - 1} \cos h (Rx) + d_{2 \cdot 2 s} \sin h (Rx) + λ_{2 \cdot 2 s - 1} x + \\ λ_{2 \cdot 2 s}, x_{2 s - 1} \leq x < x_{2 s} \\ d_{2 \cdot 2 s + 1} \cos h (Rx) + d_{2 \cdot 2 s + 2} \sin h (Rx) + λ_{2 \cdot 2 s + 1} x + \\ λ_{2 \cdot 2 s + 2}, x_{2 s} \leq x < l \end{matrix} (11) \end{matrix} \end{matrix}$

式中:λ ₁= $\begin{matrix} \frac{z_{d}}{χ K_{0}} \end{matrix}$ F₁; λ ₂=0;

λ ₃= $\begin{matrix} \frac{z_{d}}{χ K_{0}} \end{matrix} \begin{matrix} (F_{1} - P_{1}) \end{matrix}$ ;

λ ₄= $\begin{matrix} \frac{z_{d}}{χ K_{0}} \end{matrix}$ P₁x₁;

︙

λ ₂₍₂_i-₁₎₊₁= $\begin{matrix} \frac{z_{d}}{χ K_{0}} \end{matrix} \begin{matrix} (P_{1} x_{1} + P_{2} x_{2} + \dots + P_{2 i - 1} x_{2 i - 1}) \end{matrix}$ ;

λ _{2· 2}_i+₁= $\begin{matrix} \frac{z_{d}}{χ K_{0}} \end{matrix} \begin{matrix} (P_{1} x_{1} + P_{2} x_{2} + \dots + P_{2 i} x_{2 i}) \end{matrix}$ ;

︙

λ _{2· 2}_s-₁= $\begin{matrix} \frac{z_{d}}{χ K_{0}} \end{matrix}$ (F₁-P₁-P₂…P₂_i-₁-P₂_i-…-P₂_s-₁);

λ _{2· 2}_s= $\begin{matrix} \frac{z_{d}}{χ K_{0}} \end{matrix}$ (P₁x₁+P₂x₂+…+P₂_i-₁x₂_i-₁+P₂_ix₂_i+…+P₂_s-₁x₂_s-₁)。

由简支梁的边界条件及位移连续条件可得:

$\begin{matrix} \begin{matrix} \{\begin{matrix} u'_{b 0} (0) = 0, u'_{b 0} (l) = 0 \\ u'_{b 0} (x_{1})_{左} = u'_{b 0} (x_{1})_{右} \\ u ″_{b 0} (x_{1})_{左} = u ″_{b 0} (x_{1})_{右} \\ u'_{b 0} (x_{2})_{左} = u'_{b 0} (x_{2})_{右} \\ u ″_{b 0} (x_{2})_{左} = u ″_{b 0} (x_{2})_{右} \\ ︙ \\ u'_{b 0} (x_{2 i - 1})_{左} = u'_{b 0} (x_{2 i - 1})_{右} \\ u ″_{b 0} (x_{2 i - 1})_{左} = u ″_{b 0} (x_{2 i - 1})_{右} \\ u'_{b 0} (x_{2 i})_{左} = u'_{b 0} (x_{2 i})_{右} \\ u ″_{b 0} (x_{2 i})_{左} = u ″_{b 0} (x_{2 i})_{右} \\ ︙ \\ u'_{b 0} (x_{2 s - 1})_{左} = u'_{b 0} (x_{2 s - 1})_{右} \\ u ″_{b 0} (x_{2 s - 1})_{左} = u ″_{b 0} (x_{2 s - 1})_{右} \\ u'_{b 0} (x_{2 s})_{左} = u'_{b 0} (x_{2 s})_{右} \\ u ″_{b 0} (x_{2 s})_{左} = u ″_{b 0} (x_{2 s})_{右} \end{matrix} \end{matrix} \end{matrix}$ (12)

将式(11)和式(12)写成矩阵的形式, 则有:

$\begin{matrix} Cd = λ \end{matrix}$ (13)

式中:

λ = $\begin{matrix} [\begin{matrix} 0 \\ λ_{3} x_{1} + λ_{4} - λ_{1} x_{1} - λ_{2} \\ λ_{3} - λ_{1} \\ λ_{5} x_{2} + λ_{6} - λ_{3} x_{2} - λ_{4} \\ λ_{5} - λ_{3} \\ ︙ \\ λ_{2 i + 1} x_{i} + λ_{2 i + 2} - λ_{2 i - 1} x_{i} - λ_{2 i} \\ λ_{2 i + 1} - λ_{2 i - 1} \\ ︙ \\ λ_{2 \cdot 2 s + 1} x_{2 s} + λ_{2 \cdot 2 s + 2} - λ_{2 \cdot 2 s - 1} x_{2 s} - λ_{2 \cdot 2 s} \\ λ_{2 \cdot 2 s + 1} - λ_{2 \cdot 2 s - 1} \\ - λ_{2 \cdot 2 s + 1} l - λ_{2 \cdot 2 s + 2} \end{matrix}] \end{matrix}$ ;

d=[d₁d₂ … A₁ … A₂]^T

C= $\begin{matrix} [\begin{matrix} A_{3} \\ ⋱ \\ A_{4} \\ ⋱ \\ A_{5} \end{matrix}] \end{matrix}$ ;

式中:A₁=[d₂_i-₁d₂_i d₂_i+₁d₂_i+₂];

A₂=[d_{2· 2}_s-₁d_{2· 2}_s d_{2· 2}_s+₁d_{2· 2}_s+₂];

A₃= $\begin{matrix} [\begin{matrix} 1 \\ S 1_{1} & S 2_{1} & - S 1_{1} & - S 2_{1} \\ RS 2_{1} & RS 1_{1} & - RS 2_{1} & - RS 1_{1} \\ S 1_{2} & S 2_{2} & - S 1_{2} & - S 2_{2} \\ RS 2_{2} & RS 1_{2} & - S 2_{2} & - S 1_{2} \end{matrix}] \end{matrix}$ ;

A₄= $\begin{matrix} [\begin{matrix} S 1_{i} & S 2_{i} & - S 1_{i} & - S 2_{i} \\ RS 2_{i} & RS 1_{i} & - RS 2_{i} & - RS 1_{i} \end{matrix}] \end{matrix}$ ;

A₅= $\begin{matrix} [\begin{matrix} S 1_{2 s} & S 2_{2 s} & - S 1_{2 s} & - S 2_{2 s} \\ RS 2_{2 s} & RS 1_{2 s} & - RS 2_{2 s} & - RS 1_{2 s} \\ \cos h (kl) & \sin h (kl) \end{matrix}] \end{matrix}$ 。

式中:S1_i=cosh(kx_i), S2_i=sinh(kx_i), i=1, 2, …, i, …, 2s。

由式(13)可得:

$\begin{matrix} d = C^{- 1} λ (14) \end{matrix}$

将式(14)代入式(10)中即可得到各段的u'_b0, 因此进一步可得:

$\begin{matrix} v ″ (x) = \frac{M_{p} (x)}{K_{0}} + E_{b} A_{b} u'_{b 0} \frac{z_{d}}{K_{0}} (15) \end{matrix}$

根据弹性力学基本原理, 可得:

$\begin{matrix} K (x) v ″ (x) = M_{p} (x) (16) \end{matrix}$

联合式(15)(16)可得:

$\begin{matrix} K (x) = γ (x) K_{0} (17) \end{matrix}$

式中:γ $\begin{matrix} (x) \end{matrix}$ 为简支组合梁的刚度系数, γ $\begin{matrix} (x) \end{matrix}$ = $\begin{matrix} \frac{1}{1 - α (x)} \end{matrix}$ , α $\begin{matrix} (x) \end{matrix}$ = $\begin{matrix} \frac{E_{b} A_{b} u'_{b 0} (x) z_{d}}{M_{p} (x)} \end{matrix}$ 。

3 待定系数方程

3.1 同一梁段中待定系数的传递关系

以b_p+₁梁段为例, 来说明同一梁段中待定系数的传递过程。第Q个子梁段的右端与第Q+1个子梁段的左端满足变形连续和剪力、弯矩平衡的条件, 因此可得:

$Z_{b_{p + 1}}^{Q + 1} U_{b_{p + 1}}^{Q + 1} = Z_{b_{p + 1}}^{Q} U_{b_{p + 1}}^{Q} (18)$

式中：

$U_{b_{p + 1}}^{Q} = {[\begin{matrix} A_{b_{p + 1}}^{Q} & B_{b_{p + 1}}^{Q} & C_{b_{p + 1}}^{Q} & D_{b_{p + 1}}^{Q} \end{matrix}]}^{T};$

$U_{b_{p + 1}}^{Q + 1} = {[\begin{matrix} A_{b_{p + 1}}^{Q + 1} & B_{b_{p + 1}}^{Q + 1} & C_{b_{p + 1}}^{Q + 1} & D_{b_{p + 1}}^{Q + 1} \end{matrix}]}^{T};$

$Z_{b_{p + 1}}^{Q + 1} = [\begin{matrix} A_{6} & A_{7} \\ A_{8} & A_{9} \end{matrix}];$

$Z_{b_{p + 1}}^{Q} = [\begin{matrix} A_{10} & A_{11} \\ A_{12} & A_{13} \end{matrix}];$

A₆= $\begin{matrix} [\begin{matrix} 0 & 1 \\ β_{b_{p + 1}}^{Q + 1} & 0 \end{matrix}] \end{matrix}$ ;

A₇= $\begin{matrix} [\begin{matrix} 0 & 1 \\ β_{b_{p + 1}}^{Q + 1} & 0 \end{matrix}] \end{matrix}$ ;

A₈= $\begin{matrix} [\begin{matrix} 0 & - {(β_{b_{p + 1}}^{Q + 1})}^{2} K_{b_{p + 1}}^{Q + 1} \\ - {(β_{b_{p + 1}}^{Q + 1})}^{3} K_{b_{p + 1}}^{Q + 1} & 0 \end{matrix}] \end{matrix}$ ;

A₉= $\begin{matrix} [\begin{matrix} 0 & {(β_{b_{p + 1}}^{Q + 1})}^{2} K_{b_{p + 1}}^{Q + 1} \\ {(β_{b_{p + 1}}^{Q + 1})}^{3} K_{b_{p + 1}}^{Q + 1} & 0 \end{matrix}] \end{matrix}$ ;

A₁₀= $\begin{matrix} [\begin{matrix} h_{1} & h_{2} \\ β_{b_{p + 1}}^{Q} h_{2} & - β_{b_{p + 1}}^{Q} h_{1} \end{matrix}] \end{matrix}$ ;

A₁₁= $\begin{matrix} [\begin{matrix} h_{3} & h_{4} \\ β_{b_{p + 1}}^{Q} h_{4} & β_{b_{p + 1}}^{Q} h_{3} \end{matrix}] \end{matrix}$ ;

A₁₂= $\begin{matrix} [\begin{matrix} - K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{2} h_{1} & - K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{2} h_{2} \\ - K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{3} h_{2} & K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{3} h_{1} \end{matrix}] \end{matrix}$ ;

A₁₃= $\begin{matrix} [\begin{matrix} K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{2} h_{3} & K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{2} h_{4} \\ K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{3} h_{4} & K_{b_{p + 1}}^{Q} {(β_{b_{p + 1}}^{Q})}^{3} h_{3} \end{matrix}] \end{matrix}$ 。

式中:

h₁=sin $\begin{matrix} β_{b_{p + 1}}^{Q} \end{matrix} \begin{matrix} l_{b_{p + 1}}^{Q} \end{matrix}$ ;

h₂=cos $\begin{matrix} β_{b_{p + 1}}^{Q} \end{matrix} \begin{matrix} l_{b_{p + 1}}^{Q} \end{matrix}$ ;

h₃=sinh $\begin{matrix} β_{b_{p + 1}}^{Q} \end{matrix} \begin{matrix} l_{b_{p + 1}}^{Q} \end{matrix}$ ;

h₄=cosh $\begin{matrix} β_{b_{p + 1}}^{Q} \end{matrix} \begin{matrix} l_{b_{p + 1}}^{Q} \end{matrix}$ 。

由式(18)可得:

$\begin{matrix} U_{b_{p + 1}}^{Q + 1} \end{matrix}$ = $\begin{matrix} {[Z_{b_{p + 1}}^{Q + 1}]}^{- 1} \end{matrix} \begin{matrix} Z_{b_{p + 1}}^{Q} \end{matrix} \begin{matrix} U_{b_{p + 1}}^{Q} \end{matrix}$ = $\begin{matrix} T_{b_{p + 1}}^{Q} \end{matrix} \begin{matrix} U_{b_{p + 1}}^{Q} \end{matrix}$ (19)

式中: $\begin{matrix} T_{b_{p + 1}}^{Q} \end{matrix}$ 为第Q个子梁段与第Q+1个子梁段的待定系数传递矩阵。

采用递推方法便可以得到b_p+₁梁段中第1个子梁段与第m个子梁段待定系数之间的传递关系为:

$\begin{matrix} U_{b_{p + 1}}^{m} = T_{b_{p + 1}} U_{b_{p + 1}}^{1} \end{matrix}$ (20)

式中: $\begin{matrix} T_{b_{p + 1}} \end{matrix}$ 为b_p+₁梁段的待定系数传递矩阵, $\begin{matrix} T_{b_{p + 1}} \end{matrix}$ = $\begin{matrix} T_{b_{p + 1}}^{m - 1} \end{matrix} \begin{matrix} T_{b_{p + 1}}^{m - 2} \end{matrix}$ … $\begin{matrix} T_{b_{p + 1}}^{2} \end{matrix} \begin{matrix} T_{b_{p + 1}}^{1} \end{matrix}$ 。

3.2 车轮处待定系数方程

第p辆车作用处的组合梁如图4所示, 其中b_p、R_p、b_p+₁梁段分别被细划成r、s、m个子梁段。

	Figure Option View Download New Window
	图4 b_p、R_p、b_p+₁梁段划分示意图Fig.4 Sketch for divisions of sections b_p、R_p and b_p+₁

由第p辆车左轮处( $\begin{matrix} x_{1}^{p} \end{matrix}$ )的变形连续和剪力、弯矩平衡条件, 可得:

$\begin{matrix} \{\begin{matrix} {φ^{r}}_{b_{p}} ({l^{r}}_{b_{p}}) = φ_{R_{p}}^{1} (0) \\ φ {'^{r}}_{b_{p}} ({l^{r}}_{b_{p}}) = φ'_{R_{p}}^{1} (0) \\ {K^{r}}_{b_{p}} φ {″^{r}}_{b_{p}} ({l^{r}}_{b_{p}}) = K_{R_{p}}^{1} φ ″_{R_{p}}^{1} (0) \\ {K^{r}}_{b_{p}} φ {‴^{r}}_{b_{p}} ({l^{r}}_{b_{p}}) - ω^{2} m_{t 1}^{p} Y_{t 1}^{p} + k_{t 1}^{p} (Y_{t 1}^{p} - Y_{b}^{p} + \\ s_{1}^{p} a^{p} {\hat{θ}}^{p}) - K_{R_{p}}^{1} φ ‴_{R_{p}}^{1} (0) = 0 \end{matrix} \end{matrix}$ (21)

将式(5)代入式(21)中, 可得:

$\begin{matrix} H^{pl} U^{pl} = [\begin{matrix} F_{1}^{^{pl}} & F_{2}^{^{pl}} & F_{3}^{^{pl}} \end{matrix}] [\begin{matrix} {U^{r}}_{_{b_{p}}} \\ {U^{1}}_{_{R_{p}}} \\ U_{v}^{p} \end{matrix}] = 0 (22) \end{matrix}$

式中:

$\begin{matrix} F_{2}^{^{pl}} \end{matrix}$ = $\begin{matrix} [\begin{matrix} A_{14} & A_{15} \\ A_{16} & A_{17} \end{matrix}] \end{matrix}$ ;

$\begin{matrix} F_{3}^{pl} \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ - ω^{2} m_{t 1}^{p} + k_{t 1}^{p} & 0 & - k_{t 1}^{p} & s_{1}^{p} a^{p} k_{t 1}^{p} \end{matrix}] \end{matrix}$ ;

$\begin{matrix} {U^{r}}_{b_{p}} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} {A^{r}}_{b_{p}} & {B^{r}}_{b_{p}} & {C^{r}}_{b_{p}} & {D^{r}}_{b_{p}} \end{matrix}]}^{T} \end{matrix}$ ;

$\begin{matrix} {U^{1}}_{R_{p}} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} A_{R_{p}}^{1} & B_{R_{p}}^{1} & C_{R_{p}}^{1} & D_{R_{p}}^{1} \end{matrix}]}^{T} \end{matrix}$ ;

$\begin{matrix} {U^{p}}_{v} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} Y_{t 1}^{p} & Y_{t 2}^{p} & Y_{b}^{p} & {\hat{θ}}^{p} \end{matrix}]}^{T} \end{matrix}$ ;

$\begin{matrix} F_{1}^{pl} \end{matrix}$ = $\begin{matrix} [\begin{matrix} A_{18} & A_{19} \\ A_{20} & A_{21} \end{matrix}] \end{matrix}$ ;

A₁₄= $\begin{matrix} [\begin{matrix} 0 & - 1 \\ - β_{_{R_{p}}}^{1} & 0 \end{matrix}] \end{matrix}$ ;

A₁₅= $\begin{matrix} [\begin{matrix} 0 & - 1 \\ - β_{_{R_{p}}}^{1} & 0 \end{matrix}] \end{matrix}$ ;

A₁₆= $\begin{matrix} [\begin{matrix} 0 & K_{_{R_{p}}}^{1} {(β_{_{R_{p}}}^{1})}^{2} \\ K_{R_{p}}^{1} {(β_{_{R_{p}}}^{1})}^{3} & 0 \end{matrix}] \end{matrix}$ ;

A₁₇= $\begin{matrix} [\begin{matrix} 0 & - K_{_{R_{p}}}^{1} {(β_{_{R_{p}}}^{1})}^{2} \\ - K_{R_{p}}^{1} {(β_{_{R_{p}}}^{1})}^{3} & 0 \end{matrix}] \end{matrix}$ ;

A₁₈= $\begin{matrix} [\begin{matrix} h_{5} & h_{6} \\ {β^{r}}_{b_{p}} h_{6} & - {β^{r}}_{b_{p}} h_{5} \end{matrix}] \end{matrix}$ ;

A₁₉= $\begin{matrix} [\begin{matrix} h_{7} & h_{8} \\ {β^{r}}_{b_{p}} h_{8} & {β^{r}}_{b_{p}} h_{7} \end{matrix}] \end{matrix}$ ;

A₂₀= $\begin{matrix} [\begin{matrix} - {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{2} h_{5} & - {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{2} h_{6} \\ - {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{3} h_{6} & {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{3} h_{5} \end{matrix}] \end{matrix}$ ;

A₂₁= $\begin{matrix} [\begin{matrix} {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{2} h_{7} & {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{2} h_{7} \\ {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{3} h_{8} & {K^{r}}_{b_{p}} {({β^{r}}_{b_{p}})}^{3} h_{7} \end{matrix}] \end{matrix}$ 。

式中:h₅=sin $\begin{matrix} {β^{r}}_{b_{p}} \end{matrix} \begin{matrix} {l^{r}}_{b_{p}} \end{matrix}$ ; h₆=cos $\begin{matrix} {β^{r}}_{b_{p}} \end{matrix} \begin{matrix} {l^{r}}_{b_{p}} \end{matrix}$ ; h₇=sinh $\begin{matrix} {β^{r}}_{b_{p}} \end{matrix} \begin{matrix} {l^{r}}_{b_{p}} \end{matrix}$ ; h₈=cosh $\begin{matrix} {β^{r}}_{b_{p}} \end{matrix} \begin{matrix} {l^{r}}_{b_{p}} \end{matrix}$ ;

把式(20)代入式(22)可得:

$\begin{matrix} H^{pl} U^{pl} = [\begin{matrix} F_{1}^{pl} T_{b_{p}} & \begin{matrix} F_{2}^{pl} & F_{3}^{pl} \end{matrix} \end{matrix}] [\begin{matrix} {U^{l}}_{b_{p}} \\ {U^{1}}_{R_{p}} \\ U_{v}^{p} \end{matrix}] = 0 (23) \end{matrix}$

同理, 可得第p辆车右轮处的待定系数方程为:

$\begin{matrix} H^{pr} U^{pr} = [\begin{matrix} F_{1}^{pr} T_{R_{p}} & \begin{matrix} F_{2}^{pr} & F_{3}^{pr} \end{matrix} \end{matrix}] \{\begin{matrix} U_{R_{p}}^{1} \\ U_{v}^{p} \\ {U^{1}}_{b_{p + 1}} \end{matrix}\} = 0 (24) \end{matrix}$

式中: $\begin{matrix} F_{1}^{pr} \end{matrix}$ 和 $\begin{matrix} F_{3}^{pr} \end{matrix}$ 的含义同 $\begin{matrix} F_{1}^{pl} \end{matrix}$ 和 $\begin{matrix} F_{3}^{pl} \end{matrix}$ ;

$\begin{matrix} F_{2}^{pr} \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & - ω^{2} m_{t 2}^{p} + k_{t 2}^{p} & - k_{t 2}^{p} & - s_{2}^{p} a^{p} k_{t 2}^{p} \end{matrix}] \end{matrix}$ ;

$\begin{matrix} U_{b_{p + 1}}^{1} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} A_{b_{p + 1}}^{1} & B_{b_{p + 1}}^{1} & C_{b_{p + 1}}^{1} & D_{b_{p + 1}}^{1} \end{matrix}]}^{T} \end{matrix}$ 。

3.3 车辆待定系数方程

由式(4)~(7)可得:

H^pvU^pv= $\begin{matrix} [\begin{matrix} F_{1}^{pv} & \begin{matrix} F_{2}^{pv} & F_{3}^{pv} \end{matrix} \end{matrix}] \end{matrix} \begin{matrix} [\begin{matrix} U_{b_{p}}^{1} \\ U_{v}^{p} \\ {U^{1}}_{b_{p + 1}} \end{matrix}] \end{matrix}$ =0 (25)

式中: $\begin{matrix} F_{1}^{pv} \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 & k_{a 1}^{p} & 0 & k_{a 1}^{p} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] \end{matrix}$ ;

$\begin{matrix} F_{2}^{pv} \end{matrix}$ = $\begin{matrix} [\begin{matrix} A_{22} & A_{23} \\ A_{24} & A_{25} \end{matrix}] \end{matrix}$ ;

$\begin{matrix} F_{3}^{pv} \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 & 0 & 0 & 0 \\ 0 & k_{a 2}^{p} & 0 & k_{a 2}^{p} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix}] \end{matrix}$ ;

式中:

A₂₂=

$\begin{matrix} [\begin{matrix} - ω^{2} m_{t 1}^{p} + k_{a 1}^{p} + k_{t 1}^{p} & 0 \\ 0 & - ω^{2} m_{t 2}^{p} + k_{a 2}^{p} + k_{t 2}^{p} \end{matrix}] \end{matrix}$ ;

A₂₃= $\begin{matrix} [\begin{matrix} - k_{t 1}^{p} & s_{1}^{p} a^{p} k_{t 1}^{p} \\ - k_{t 2}^{p} & - s_{2}^{p} a^{p} k_{t 2}^{p} \end{matrix}] \end{matrix}$ ;

A₂₄= $\begin{matrix} [\begin{matrix} - k_{t 1}^{p} & - k_{t 2}^{p} \\ s_{1}^{p} a^{p} k_{t 1}^{p} & - s_{2}^{p} a^{p} k_{t 2}^{p} \end{matrix}] \end{matrix}$ ;

A₂₅=

$\begin{matrix} [\begin{matrix} - ω^{2} m_{b}^{p} + k_{t 1}^{p} + k_{t 2}^{p} & s_{2}^{p} a^{p} k_{t 2}^{p} - s_{1}^{p} a^{p} k_{t 1}^{p} \\ s_{2}^{p} a^{p} k_{t 2}^{p} - s_{1}^{p} a^{p} k_{t 1}^{p} & B_{1} \end{matrix}] \end{matrix}$ 。

B₁=[-ω ² $\begin{matrix} I_{b}^{p} \end{matrix}$ + $\begin{matrix} {(a^{p})}^{2} \end{matrix} \begin{matrix} ({(s_{2}^{p})}^{2} k_{t 2}^{p} + {(s_{1}^{p})}^{2} k_{t 1}^{p}) \end{matrix}$ ]。

3.4 边界处待定系数方程

由简支梁左端的边界条件, 可得:

$\begin{matrix} H_{s 1} U_{b_{1}}^{1} = 0 (26) \end{matrix}$

式中:H_s₁= $\begin{matrix} [\begin{matrix} 0 & 1 & 0 & 1 \\ 0 & - 1 & 0 & 1 \end{matrix}] \end{matrix}$ 。

将第b_s+₁梁段划分成q个子梁段, 最后一个子梁段的长度为 $\begin{matrix} l_{b_{s + 1}}^{q} \end{matrix}$ 。根据简支梁右端的边界条件可得:

$\begin{matrix} H_{s 2} T_{b_{s + 1}} U_{b_{s + 1}}^{1} = 0 (27) \end{matrix}$

式中:

H_s₂= $\begin{matrix} [\begin{matrix} A_{26} & A_{27} \end{matrix}] \end{matrix}$ ;

$\begin{matrix} T_{b_{s + 1}} \end{matrix}$ 为b_s+₁梁段的待定系数传递矩阵;

A₂₆= $\begin{matrix} [\begin{matrix} \sin β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} & \cos β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} \\ - \sin β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} & - \cos β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} \end{matrix}] \end{matrix}$ ;

A₂₇= $\begin{matrix} [\begin{matrix} \sin h β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} & \cos h β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} \\ \sin h β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} & \cos h β_{b_{s + 1}}^{q} l_{b_{s + 1}}^{q} \end{matrix}] \end{matrix}$ 。

4 动力特性的求解

当组合梁上作用有s辆车时, 组合梁被分割成2s+1个梁段。车辆和组合梁耦合振动系统共有12s+4个待定系数, 而能够列出的待定系数方程也刚好为12s+4个, 因此可以采用类似传统有限元方法中的数值组装方法来构成车辆作用下简支组合梁的待定系数振动方程。

$\begin{matrix} HU = 0 (28) \end{matrix}$

式中:

$m = 12 (p - 1) + 2;$

$n = 4 [2 (p - 1) + (p - 1)] = 12 (p - 1);$

$m' = 12 s + 2;$

$n' = 4 (2 s + s) = 12 s 。$

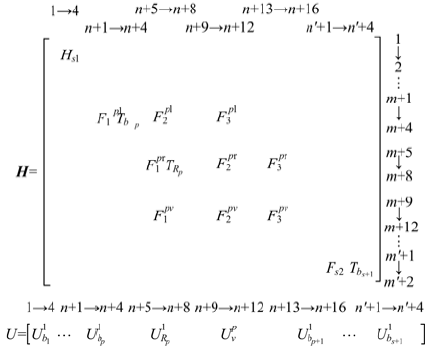
由于式(28)中U元素不全为0, 所以要求:

$\begin{matrix} |H| = 0 (29) \end{matrix}$

采用半区间法便可以从式(29)中求解出各阶自振频率及其对应的待定系数^[14]。得到自振频率和待定系数数值后, 利用各梁段中待定系数的传递关系便可得到车辆作用下组合梁的振型。

5 数值算例

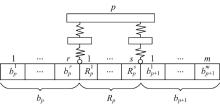
采用本文方法计算了两个车辆作用下一座钢-混凝土组合梁的自振频率和振型。组合梁的跨径为35 m, 横截面如图5所示。车辆在组合梁上的作用位置如图6所示。车辆参数为:车轮质量m_t1=m_t2=1500 kg; 车体转动惯量2.4× 10⁵ kg· m²; 车体质量m_b=1.77× 10⁴ kg; 悬架刚度k_t1=k_t2=4× 10⁶ N/m; 轮胎刚度k_a1=k_a2=5× 10⁶ N/m; 车轮间距a=4 m; s₁=s₂=0.5。同时采用文献[13]中所述的有限元方法对该数值算例也进行了计算。自振频率计算结果列于表1中, 振型如图7所示。

	Figure Option View Download New Window
	图5 组合梁横断面图Fig.5 Cross section of composite beam

	Figure Option View Download New Window
	图6 车辆作用位置Fig.6 Positions of vehicles

表1 频率计算值 Table 1 Calculation results of frequency

	Figure Option View Download New Window
	图7 振型计算结果Fig.7 Calculation results of mode shape

由自振频率计算结果可知, 采用本文方法和有限元方法计算出的前3阶自振频率的最大误差为0.6%。并且两种方法计算出的振型也十分接近。因此可以认为采用本文方法计算车辆作用下组合梁的动力特性是有效和可靠的。

6 结束语

在考虑车辆竖向荷载对组合梁结合面剪切滑移效应产生影响的基础上, 得到车辆作用下组合梁的刚度分布函数。进而基于传递矩阵方法的基本思想, 根据力的平衡和变形协调条件, 形成了车辆作用下钢-混凝土简支梁动力特性的求解方法, 并把该方法应用到一座组合梁的数值算例中。数值算例结果表明, 采用本文方法和有限元方法计算出的前3阶自振频率的最大误差为0.6%, 并且两种方法计算出的振型也十分接近, 充分说明了本文方法的可靠性和有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	侯忠明, 夏禾, 王元清, 等. 钢-混凝土组合梁动力折减系数研究[J]. 振动与冲击, 2015, 34(4): 74-81. Hou Zhong-ming, Xia He, Wang Yuan-qing, et al. Dynamic reduction coefficients for a steel-concrete composite beam[J]. Journal of Vibration and Shock, 2015, 34(4): 74-81. [本文引用:1]
[2]	王景全, 殷惠光, 张书兵, 等. 钢-混凝土组合梁考虑界面滑移的振动模态试验研究[J]. 建筑结构学报, 2016, 37(2): 142-149. Wang Jing-quan, Yin Hui-guang, Zhang Shu-bing, et al. Experimental investigation on dynamic properties of steel-concrete composite beams considering effect of interfacial slip[J]. Journal of Building Structures, 2016, 37(2): 142-149. [本文引用:1]
[3]	程永春, 谭国金, 刘寒冰, 等. 简支梁桥动态检测中跳车激励方法理论研究[J]. 振动工程学报, 2009, 22(5): 474-479. Cheng Yong-chun, Tan Guo-jin, Liu Han-bing, et al. Research of vehicle bump excitation in dynamic detection of simple supported bridge[J]. Journal of Vibration Engineering, 2009, 22(5): 474-479. [本文引用:1]
[4]	谭国金. 中小跨径梁式桥动力检测技术及损伤识别方法研究[D]. 长春: 吉林大学交通学院, 2009. Tan Guo-jin. Dynamic detection technique and damage identification method for beam bridges with small and medium span[D]. Changchun: College of Transportation, Jilin University, 2009. [本文引用:1]
[5]	谭国金, 刘子煜, 王龙林, 等. 车辆作用下中小跨径裂缝简支梁桥自振特性分析[J]. 振动工程学报, 2016, 29(5): 831-841. Tan Guo-jin, Liu Zi-yu, Wang Long-lin, et al. Free vibration analysis of a small or medium-span cracked simply supported bridge considering bridge-vehicle interaction[J]. Journal of Vibration Engineering, 2016, 29(5): 831-841. [本文引用:1]
[6]	Kim C Y, Jung D S, Kim N S, et al. Effect of vehicle weight on natural frequencies of bridges measured from traffic-induced vibration[J]. Earthquake Engineering and Engineering Vibration, 2003, 2(1): 109-115. [本文引用:1]
[7]	苏木标, 梁振辉. 对车-桥系统自振特性的初探[J]. 石家庄铁道学院学报, 1993, 6(3): 49-58. Su Mu-biao, Liang Zhen-hui. A study of the free vibration characteristics of VBS[J]. Journal of Shijiazhuang Railway Institute, 1993, 6(3): 49-58. [本文引用:1]
[8]	de Roeck G, Maeck J, Michielsen T, et al. Traffic-induced shifts in modal properties of bridges[J]. The International Society for Optical Engineering, 2002, 4753: 630-636. [本文引用:1]
[9]	程永春, 谭国金, 刘寒冰, 等. 车辆作用下的公路简支梁桥测试频率[J]. 吉林大学学报: 工学版, 2009, 39(6): 1492-1496. Cheng Yong-chun, Tan Guo-jin, Liu Han-bing, et al. Test frequencies freely supported beam of highway bridge under effect of vehicles[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(6): 1492-1496. [本文引用:1]
[10]	Tan Guo-jin, Wang Wen-sheng, Jiao Yu-bo. Free vibration analysis of a cracked simply supported bridge considering bridge-vehicle interaction[J]. Journal of Vibroengineering, 2016, 18(6): 3608-3635. [本文引用:1]
[11]	谭国金, 宫亚峰, 程永春, 等. 基于有载频率的简支梁桥自振频率计算方法[J]. 振动工程学报, 2011, 24(1): 31-35. Tan Guo-jin, Gong Ya-feng, Cheng Yong-chun, et al. Calculation for natural frequency of simply supported beam bridges based on loaded frequency[J]. Journal of Vibration Engineering, 2011, 24(1): 31-35. [本文引用:1]
[12]	刘寒冰, 时成林, 谭国金. 考虑剪切滑移效应的叠合梁有限元解[J]. 吉林大学学报: 工学版, 2016, 46(3): 792-797. Liu Han-bing, Shi Cheng-lin, Tan Guo-jin. Finite element solution of composite beam with effect of shear slip[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(3): 792-797. [本文引用:2]
[13]	时成林. 季冻区中小跨径桥梁桥面铺装及考虑其影响的主梁受力特性研究[D]. 长春: 吉林大学交通学院, 2016. Shi Cheng-lin. Research on bridge deck pavement and mechanical characteristics of girder considering the influencing of deck pavement for medium-small span bridges in seasonal frozen area[D]. Changchun: College of Transportation, Jilin University, 2016. [本文引用:1]
[14]	Lin H Y, Tsai Y C. Free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems[J]. Journal of Sound and Vibration, 2007, 302(3): 442-456. [本文引用:1]

2015

0.0

. 2015, 34(4):74-81

Dynamic reduction coefficients for a steel-concrete composite beam

钢-混凝土组合梁动力折减系数研究

Hou Zhong-ming , Xia He , Wang Yuan-qing

侯忠明, 夏禾, 王元清

... 0 引言由于钢-混凝土组合梁具有能够充分发挥钢材的抗拉性能强、混凝土抗压强度高的材料优势,并且能够自架设施工、建筑垃圾少等优点,在桥梁工程领域得到了越来越广泛的应用^[1,2] ...

2016

0.0

. 2016, 37(2):142-149 DOI:doi:10.14006/j.jzjgxb.2016.02.018

Experimental investigation on dynamic properties of steel-concrete composite beams considering effect of interfacial slip

钢-混凝土组合梁考虑界面滑移的振动模态试验研究

Wang Jing-quan , Yin Hui-guang , Zhang Shu-bing

王景全, 殷惠光, 张书兵

摘　要：为研究钢与混凝土的界面滑移效应对钢一混凝土组合梁基本动力性能的影响程度和规律，进行了5根跨度3．8133的简支钢一混凝土组合梁的静载和振动模态试验，其中4根采用抗剪栓钉，剪力连接度分别为0．6、0．7、1．0和1．4，另1根采用能提供刚性抗剪连接的开孔钢板连接件。试验结果表明：在静载作用下，随剪力连接度的提高，组合梁的界面滑移减小，抗弯刚度显著增加。竖弯模态试验中，剪力连接度小于等于1．0的3根梁，其前4阶竖向弯曲模态频率与采用开孔钢板抗剪连接件的试验梁相比均有减小，最小减幅为9．8％，最大减幅达26％；剪力连接度为1，4的梁较开孔钢板连接件的试验梁，基频减小了6．1％，第2～4阶自振频率减小幅度均在10％以上，与连接度为0．6的梁相比，其基频增大了13．2％；试验梁的模态阻尼比随着剪力连接度的增大而减小。扭转模态试验中，各阶扭转模态频率差异程度在7％以内，变化规律不明显。由此可见，钢与混凝土板的界面滑移效应对组合梁竖向弯曲自振频率的影响不容忽视，在设计计算中须予以考虑。试验结果可为工程动力分析榀供参考。

2009

0.0

. 2009, 22(5):474-479

Research of vehicle bump excitation in dynamic detection of simple supported bridge

简支梁桥动态检测中跳车激励方法理论研究

Cheng Yong-chun , Tan Guo-jin , Liu Han-bing

程永春, 谭国金, 刘寒冰

... 在桥梁的动力特性测试过程中,为了获得具有较高信噪比的响应信号,往往采用车辆对桥梁进行激振,例如采用通行车辆、跳车试验^[3]及跑车试验等 ...

2009

0.0

. 2009, :-

Dynamic detection technique and damage identification method for beam bridges with small and medium span

中小跨径梁式桥动力检测技术及损伤识别方法研究[D]

Tan Guo-jin.

谭国金

本文结合吉林省交通科技项目“混凝土梁式桥承载能力快速评估技术研究与系统开发”(2008-1-1)和国家高技术研究发展计划(863项目)“季节冰冻区大范围道路灾害参数监测与辨识预警系统研究”(2009AA11Z104),开展了以下几方面的研究工作: 1、基于车桥耦合振动特性,应用达朗伯原理和欧拉-柏努利梁假设,建立了跳车激励全过程动力响应计算的理论模型,并从理论上明确了极限跳车高度的计算方法,为跳车试验的顺利进行提供了理论保障。 2、基于模态综合分析方法,建立了跑车激励全过程的三维空间车-桥耦合振动分析模型。基于车-桥耦合振动分析模型,分析了车辆参数,桥面平整度、行车速度和车辆作用位置对桥梁冲击效应的影响规律。 3、在不考虑轮胎刚度的情况下和在考虑轮胎刚度的情况下,分别建立了多个车辆—简支梁桥系统相互作用的理论模型,利用模态分析方法和自由振动理论,求解出车辆作用下的桥梁有载频率。并且给出了单个车辆作用下,桥梁有载频率的解析表达式。基于推导出的理论计算模型,讨论了多种影响因素对桥梁频率变化值(桥梁的有载频率与固有频率之间的差值)的影响规律。 5、基于单个车辆作用下的桥梁有载频率解析表达式,建立了桥梁有载频率(测试频率)与固有频率的解析表达式,此表达式可用来从测试到的有载频率计算出桥梁的固有频率。 6、提出了一种仅利用测点位移自由衰减响应来识别桥梁结构动力参数的方法,此识别算法可以识别出桥梁结构的频率、振型和阻尼比三大动力参数,并且识别精度较高。在识别过程中采用三次样条曲线对位移响应进行预处理,保证了识别过程的稳定性。 7、建立了基于灵敏度矩阵的梁式桥损伤识别方法,此损伤识别方法可以较精确的识别中小跨径梁式桥的损伤。利用矩阵摄动理论形成动力参数的灵敏矩阵,避免了求解灵敏度过程的偏微分计算,提高了此识别方法的实用性。采用现代数学方法,对此损伤识别方法的统计特性进行了分析,即确定了识别出的损伤程度的不确定性。

... 有关研究成果表明,测试到的车辆作用下的桥梁频率实际上是以桥梁振动为主要振动形式的车桥耦合振动系统的频率,车辆作用下的桥梁频率与桥梁的自振频率存在一定的差异,有时这种差异甚至可以掩盖桥梁自身损伤导致的自振频率变化^[4,5] ...

2016

0.0

. 2016, 29(5):831-841 DOI:doi:10.16385/j.cnki.issn.1004-4523.2016.05.010

Free vibration analysis of a small or medium-span cracked simply supported bridge considering bridge-vehicle interaction

车辆作用下中小跨径裂缝简支梁桥自振特性分析

Tan Guo-jin , Liu Zi-yu , Wang Long-lin

谭国金, 刘子煜, 王龙林

摘　要：基于传递矩阵方法的基本思想,形成了车辆作用下裂缝简支梁桥自振特性的分析方法。在确定了简支梁桥及车辆简化模型的基础上,首先明确了表征梁体振动形状的待定系数在裂缝间的传递关系,接着从结构振动的基本原理出发,建立了车轮处梁体待定系数方程和表征车辆振动的待定系数方程。其次采用数值组装方法把车轮处的待定系数方程、车辆振动待定系数方程以及边界条件组合成了一个新型的车辆-裂缝简支梁耦合体系自由振动方程,通过求解该方程便可得到车辆作用下裂缝简支梁桥的自振特性。最后采用多种工况下的数值模拟计算来验证该方法的正确性和有效性。

2003

0.0

... Kim等^[6]通过对Nongro桥的实验监测,得出了轻车辆作用下的桥梁频率比重车辆作用下的桥梁频率高5 ...

1993

0.0

. 1993, 6(3):49-58

A study of the free vibration characteristics of VBS

对车-桥系统自振特性的初探

Su Mu-biao , Liang Zhen-hui.

苏木标, 梁振辉

... 苏木标等^[7]从车-桥耦合振动的基本原理出发,探讨了车辆对简支梁桥自振频率的影响 ...

2002

0.0

... de Roeck等^[8]采用有限元方法计算了车辆作用下连续梁桥的自振频率 ...

2009

0.0

. 2009, 39(6):1492-1496

Test frequencies freely supported beam of highway bridge under effect of vehicles

车辆作用下的公路简支梁桥测试频率

Cheng Yong-chun , Tan Guo-jin , Liu Han-bing

程永春, 谭国金, 刘寒冰

A theoretical model was established for the interaetion of the multiple-vehicle and bridge system using the D'Alembert principle and the hypothesis of Euler-Bernoulli beam. The motion equation of the vehicle-bridge system was decoupled by the model analysis method. The decoupled motion equation expressed in the matrix form of the generalized coordinates was solved by the eigenvibration theory to get the frequencies of the bridge loaded by vehicles. For the highway bridges with small or medium span, their vibrations were excited usually by a single vehicle, and the vehicle will stay on the bridge after excitation, so analytical expressions of the frequencies of the bridge under the action of a single vehicle were derived. The effects of the location of vehicle, the stiffness of its suspension spring, the mass above and under the spring on the difference between the loaded frequencies and the eigenfrequencies of the bridge were discussed.

应用达朗伯（D'Alembert）原理和欧拉柏努利梁（Euler-Bernoulli）假设，建立了多个车辆-桥梁系统相互作用的理论模型。利用模态分析方法，使车辆-桥梁系统方程解耦，基于广义坐标的自由振动理论，对用广义坐标矩阵形式表示的解耦后的运动方程用固有振动理论求解，从而得出多个车辆作用下的桥梁有载频率。对于中小跨径的公路桥梁，往往采用单个车辆激振桥梁，激振后停于桥上，因此推导出了单个车辆作用下的桥梁有载频率解析表达式。讨论了车辆的位置、弹簧刚度、簧上质量、簧下质量和桥梁有载频率与桥梁固有频率差值之间的关系。

... 程永春^[9]、Tan等^[10]形成了车辆作用下完好简支梁桥自振和裂缝简支梁桥自振频率的计算方法,并提出了剔除车辆对桥梁自振频率影响的方法^[11] ...

2016

0.0

... 程永春^[9]、Tan等^[10]形成了车辆作用下完好简支梁桥自振和裂缝简支梁桥自振频率的计算方法,并提出了剔除车辆对桥梁自振频率影响的方法^[11] ...

2011

0.0

. 2011, 24(1):31-35

Calculation for natural frequency of simply supported beam bridges based on loaded frequency

基于有载频率的简支梁桥自振频率计算方法

Tan Guo-jin , Gong Ya-feng , Cheng Yong-chun

谭国金, 宫亚峰, 程永春

... 程永春^[9]、Tan等^[10]形成了车辆作用下完好简支梁桥自振和裂缝简支梁桥自振频率的计算方法,并提出了剔除车辆对桥梁自振频率影响的方法^[11] ...

2016

0.0

. 2016, 46(3):792-797

Finite element solution of composite beam with effect of shear slip

考虑剪切滑移效应的叠合梁有限元解

Liu Han-bing , Shi Cheng-lin , Tan Guo-jin.

刘寒冰, 时成林, 谭国金

... 有关研究资料^[12,13]表明,钢-混组合梁的抗弯性能不仅取决于钢梁的抗弯刚度和混凝土顶板的抗弯刚度,钢-混结合面的剪切滑移效应也是影响其抗弯性能的因素 ...

... 在弯矩M_p(x)作用下,混凝土顶板形心轴处的应变为^[12]: ...

2016

0.0

. 2016, :-

Research on bridge deck pavement and mechanical characteristics of girder considering the influencing of deck pavement for medium-small span bridges in seasonal frozen area

季冻区中小跨径桥梁桥面铺装及考虑其影响的主梁受力特性研究[D]

Shi Cheng-lin.

时成林

对于中小跨径桥梁而言,桥面铺装的主要功能是保护主梁,即避免车轮荷载直接磨耗行车道板和防止水分渗入到桥面板,同时不可避免要参与主梁受力,为主梁分担荷载。由于桥面铺装结构形式的复杂性和使用条件的恶劣性,导致桥面铺装出现病害的现象屡屡发生,并且破坏形式还具有明显的地域特点。我国中小跨径混凝土桥梁量大面广,即使是简单的维护也需投入大量的资金,因此开展中小跨径桥梁的桥面铺装研究十分必要。其研究意义主要体现在两个方面:一方面是在恶劣的使用条件下,如何避免或减少桥面铺装本身的病害;另一方面是中小跨径桥梁的梁高不大,刚度较小,桥面铺装参与主梁受力的程度较高,如何把握其影响,准确的计算主梁受力特性对于桥梁检测等工作意义非凡。在避免或减少桥面铺装本身的病害方面,人们围绕桥面铺装构造形式、材料及受力状态分析开展了大量的研究工作。由于水泥混凝土铺装层与桥面板的粘结性能要强于沥青混凝土铺装层与水泥混凝土铺装层的粘结性能,人们普遍关注的是沥青混凝土铺装层与水泥混凝土铺装层的粘结特性,常常忽视水泥混凝土铺装层与桥面板之间的粘结特性。有关研究资料表明,二者结合面会出现滑动,在车辆、温度等荷载的反复作用下甚至发生剪切破坏。在考虑桥面铺装的主梁受力特性分析方面,目前的研究成果比较少。其实水泥混凝土铺装层与桥面板之间的接触既不是完全结合、也不是完全脱离,水泥混凝土铺装层与桥面板之间的接触状态直接影响了桥面铺装参与主梁受力的程度。对于中小跨径混凝土桥梁的检测而言,如果不能在进行主梁受力状态分析时,定量的把握层间接触状态,准确的考虑桥面铺装的影响,会导致测试到的主梁力学特性与理论计算值之间存在较大差异,从而使得桥梁状态评估结果不够准确。通过文献检索还未发现以层间接触状态的定量表达为基础,考虑桥面铺装影响的主梁受力特性计算方法。为了解决上述问题,本文结合吉林省重大科技攻关项目“季冻区桥梁绿色生态桥面铺装材料研究及产品开发”和交通运输部西部交通建设科技项目“季冻区公路应对极端气候的快速维护与安全保障技术研究”,开展了季冻区中小跨径混凝土桥梁桥面铺装构造形式及考虑桥面铺装的主梁受力特性方法研究。以改善层间粘结能力为出发点,提出了一种适用于季冻区中小跨径混凝土桥梁的桥面铺装构造形式。该构造最大特点是在原有钢筋连接的基础上,在桥面板上设置凹槽,以改善水泥混凝土铺装层和桥面板之间的粘结能力。采用自行设计的试验装置,测试了不同条件下防水粘结层的粘结性能,并分析了其温度敏感性。设计了22组不同配筋率和不同凹槽间距、凹槽尺寸等参数情况下水泥混凝土铺装层与桥面板层间剪切试件,测试了各组试件的剪切性能,并分析了各参数对剪切性能的影响。提出采用抗剪刚度来定量表征层间接触状态,并给出了水泥混凝土铺装层与桥面板的层间抗剪刚度及剪切强度经验公式。为了能够准确计算考虑桥面铺装的主梁受力状态,采用抗剪刚度来体现层间接触状态,形成了考虑桥面铺装的单梁静力特性分析方法;对刚接梁法进行改进,建立了能够考虑桥面铺装影响的桥梁横向分布系数计算方法。并将上述方法应用到一座30m跨径简支T梁桥的实际工程中。车辆作用会导致桥梁动力特性的变异,桥面铺装同样会影响桥梁的动力特性。如何分析出车辆和桥面铺装共同影响下的主梁动力特性对于桥梁检测或监测来说意义重大。以水泥混凝土铺装层与桥面板之间层间抗剪刚度为基础,考虑桥面铺装对主梁刚度的贡献,形成了车辆作用下考虑桥面铺装的主梁动力特性计算方法。

2007

0.0

... 采用半区间法便可以从式(29)中求解出各阶自振频率及其对应的待定系数^[14] ...